Engineering
Vol. 4 No. 4 (2012) , Article ID: 18818 , 9 pages DOI:10.4236/eng.2012.44024
Automotive Ride Comfort Control Using MR Fluid Damper
University of Helwan, Cairo, Egypt
Email: mahmoud.el-kafafy@vub.ac.be, eldemerdash40@yahoo.com, eladlmr@hotmail.com
Received January 10, 2012; revised February 10, 2012; accepted February 20, 2012
Keywords: Ride Comfort; Rheological Fluid Damper; Vibration Control
ABSTRACT
In this paper, the performance of automotive ride comfort using Bouc-Wen type magneto-rheological (MR) fluid damper is studied using a two degree of freedom quarter car model. The sliding mode control is used to force the MR damper to follow the dynamics of ideal sky-hock model. The model is tested on two excitations, the first is a road hump with severe peak amplitude and the second is a statistical random road. The results are generated and presented in time and frequency domains using Matlab/Simulink software. Comparison with the fully active, ideal semi-active and conventional passive suspension systems are given as a root mean square values. Simulation results, for the designed controller, show that with the controllable MR damper has a significant improvement for the vehicle road holding then its lateral stability as well as road damage in comparison with passive, fully active and ideal semi-active suspension systems.
1. Introduction
The function of automotive suspension system is not only to isolate the effect of road surface irregularities on the passengers to improve the ride comfort but also it has to control the dynamic tyre load with acceptable suspension working space to enhance the vehicle stability and safety. The dynamic tyre load is the main affect of tyre/road friction forces which controlling the vehicle lateral stability during handling maneuvers and braking, stopping distance, traction forces as well as tyre rolling resistance [1]. Semi-active suspension, which has the principle of controlling energy dissipation, is accepted for automotive manufacturers since they can achieve a desirable performance than passive suspension and there are no external power source requirements (other than for control valve actuation) and much more simple in comparison with fully active suspension [2-6]. Most of previous research work in semi-active suspensions considered that the damping force can be controlled through mechanical changing for the damper orifice using hydraulic valves. These valves are noisy, its maintenance costly and have drawback in their time delay. As technology advances, a semi-active suspension using smart fluids with an adjustable viscosity to control the damper damping force, instead of hydraulic valves, has a considerable attention [7-16]. These smart fluid dampers are classified into two types Electro-rheological (ER) and Magneto-rheological (MR) dampers. These fluids can reversibly change instantaneously from a free-flowing liquid to a semi-solid with controllable yield strength when exposed to a magnetic field or electric current with maximum power supply of 50 Watt [8]. The main electrical difference between these fluids is that the MR fluid damper uses a power supply voltage from 2 to 25 Volt while the ER fluid damper uses a power supply voltage form 2000 to 5000 Volt. According to these electrical specifications, the MR fluid damper has been used in seat suspensions for trucks since 1998 in USA and recently the MR damper in production for the main suspension of passenger cars.
From literature, several mechanical models have been proposed to describe the performance of MR dampers and their behavior [9-17]. A Bouc-Wen model, which was described by Spencer et al. [8], is still the most commonly used model to describe the MR damper hysteretic characteristics. The problem with the other models such that neural network [9] and fuzzy [10] models is that it is always requires a training to derive a reasonable model with its nonlinearity complexity and only applicable to achieve the desirable damper force in an open-loop control system. The limitation with the polynomial curve fitting models [11] is that it cannot characterize the MR behavior well at low velocity region since the model does not include variables characterizing the pre-yield property of the damper force. Other Models black box [12], NARX-based technique [13] and simplified inverse dynamics [14] are more flexible to describe the behavior of the MR dampers, but the correlation between the model parameters and hysteresis phenomena is not clear. Further simplified models are needed in order to reduce the computational complexity in real world microcontrollers; however the nonlinearity of magneto-rheological (MR) dampers is not only from the hysteresis but also from the damper bi-linearity and the saturation related to the fluid magnetism [15].
In this paper, the mathematical model for MR damper using the Bouc-Wen model to characterize hysteresis behavior is adapted from Spencer et al. [7]. Based on quarter car with two degrees of freedom, an ideal skyhock model is used as reference model and the sliding mode control technique is applied to consider load uncertainty in result a robust control system. The model is tested on two excitations; road hump and random profile and the results are generated and presented in time and frequency domains. Comparisons with the conventional passive, fully active and ideal semi-active are given as a root mean square values.
2. Quarter Car Model with MR-Damper
A car suspension includes an MR-damper is modeled as shown in Figure 1, the figure shows a two degree of freedom system represents a quarter car model. The mass of the vehicle is represented by the sprung mass  and the mass of the wheel and associated components is represented by the unsprung mass
and the mass of the wheel and associated components is represented by the unsprung mass . The two masses vertical motions are described by the displacements
. The two masses vertical motions are described by the displacements 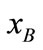 and
and 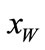 for sprung and unsprung mass respectively. The road excitation disturbance is represented by
for sprung and unsprung mass respectively. The road excitation disturbance is represented by 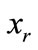 and the passive spring and tyre stiffness are
and the passive spring and tyre stiffness are  and
and 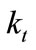 respectively neglecting the tyre damping compared to the system damping.
respectively neglecting the tyre damping compared to the system damping.
By applying Newton second law to the quarter car model, the equations of motion for the masses 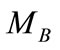 and
and 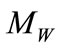 are:
are:
 (1)
(1)
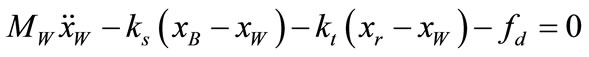 (2)
(2)
where 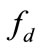 is the MR damper force is;
is the MR damper force is;
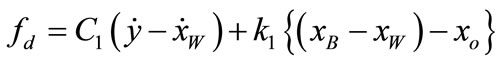 (3)
(3)
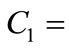 viscous damping coefficient which produce the system roll-off at low velocities, see Figure 1.
viscous damping coefficient which produce the system roll-off at low velocities, see Figure 1.
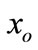 = initial deflection for the damper accumulator which is represented by the stiffness
= initial deflection for the damper accumulator which is represented by the stiffness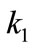 .
.
 (4)
(4)
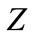 = Bouc-Wen variable governed by
= Bouc-Wen variable governed by
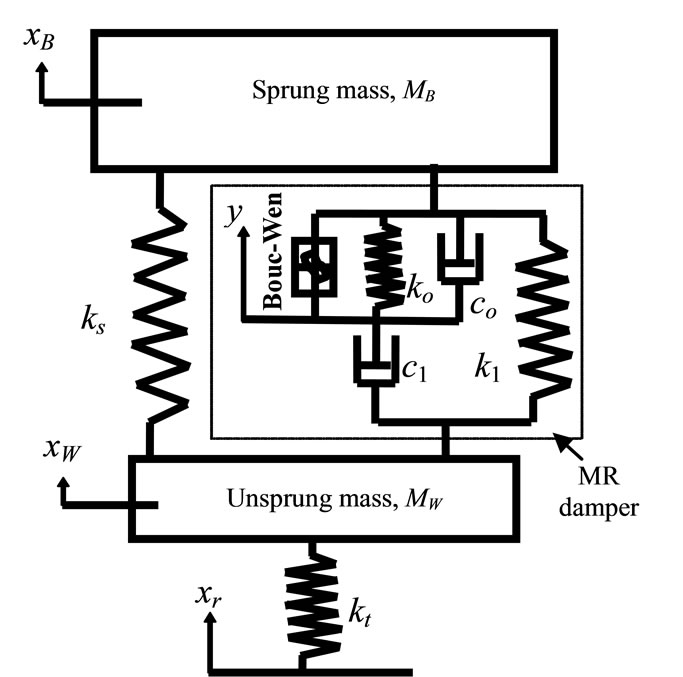
Figure 1. Quarter car model with MR damper.
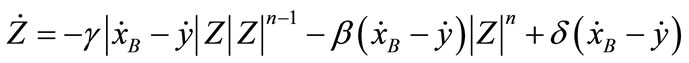 (5)
(5)
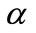 and
and 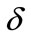 are functions of the applied magnetic field and related to the height, width and slope of the pre-yield hysteresis loop.
are functions of the applied magnetic field and related to the height, width and slope of the pre-yield hysteresis loop.
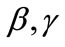 and
and 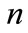 give the basic configuration of the hysteresis loop.
give the basic configuration of the hysteresis loop.
In order to consider the damper force 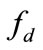 is dependent on the input voltage, the following linear relations can be used [7,18]:
is dependent on the input voltage, the following linear relations can be used [7,18]:
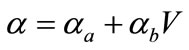 (6)
(6)
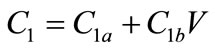 (7)
(7)
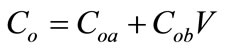 (8)
(8)
where  is given by the following differential equation:
is given by the following differential equation:
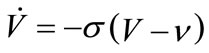 (9)
(9)
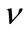 = the voltage applied to the damper
= the voltage applied to the damper
 is a constant governing the rate of change of magnetic field to reach the equilibrium of the MR fluid.
is a constant governing the rate of change of magnetic field to reach the equilibrium of the MR fluid.
The MR damper model parameters are adapted from [17] and given in Table 1.
3. Suspension System Controller
In this controller, the ideal skyhook is used as a reference model and the sliding mode control technique is used to force the system sprung mass motion to track the sprung mass motion of the reference model. The Since the suspension system is a second order system, then sliding mode surface is given by [18,19]:
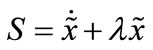 (10)
(10)
where 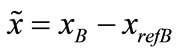
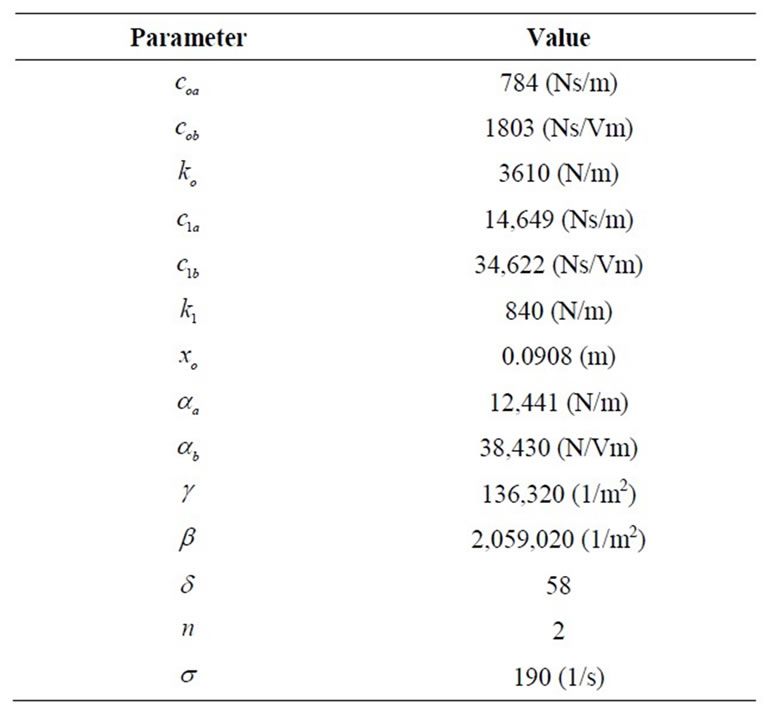
Table 1. Parameters of MR damper model.
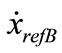 is the body state variable for the reference model.
is the body state variable for the reference model.
The sliding condition must be defined to ensure that the states will move toward and reach the sliding surface. The proposed sliding condition [18] is:
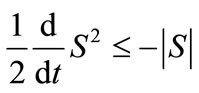 (11)
(11)
Or
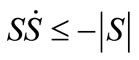 (12)
(12)
The damping force is obtained by differentiation of Equation (10) as:
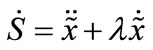 (13)
(13)
From Equations (6)-(8), by substituting  in Equations (6)-(20), we get,
in Equations (6)-(20), we get,
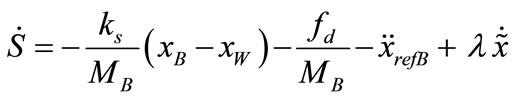 (14)
(14)
The best approximation for the desired damping force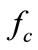 , a control law should achieve
, a control law should achieve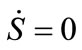 , thus;
, thus;
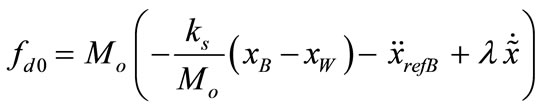 (15)
(15)
To account for the mass uncertainty while satisfying the sliding condition a term discontinuous across the surface is added to the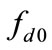 , then take the control law or the desired damping force as:
, then take the control law or the desired damping force as:
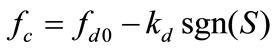 (16)
(16)
where sgn is the surface function sign and 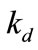 is a switching gain. Hence, using Equation (16), the system trajectory will take finite time to reach the surface
is a switching gain. Hence, using Equation (16), the system trajectory will take finite time to reach the surface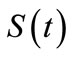 , after which the error will exponentially go to zero. An ideal sliding mode exists only when the state trajectory
, after which the error will exponentially go to zero. An ideal sliding mode exists only when the state trajectory 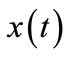 of the controlled plant agrees with the desired trajectory at every time. To avoid the chattering problem in the sliding surface, Equation (16) becomes [18],
of the controlled plant agrees with the desired trajectory at every time. To avoid the chattering problem in the sliding surface, Equation (16) becomes [18],
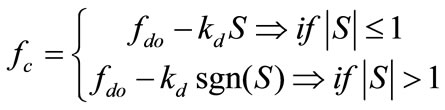 (17)
(17)
More details for sliding mode control technique can be found in many Refs. [18-20].
4. The Damper Control Strategy
In this section, the MR damper controller is described as a continuous state control strategy. Figure 2 shows a block diagram for this controller. As shown the MR damper damping force 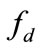 is a feedback signal compared to the system desired force
is a feedback signal compared to the system desired force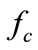 , which was calculated based on the sliding mode control and reference model. To guarantee that the control signal sent to the damper is not to generate energy, the control function is enabled only when the direction of the desired damping force and the error having the same direction. If the control function and the desired force have different sign, then the damper input voltage is set to zero. Mathematically, the continuous control strategy can be represented by [18]:
, which was calculated based on the sliding mode control and reference model. To guarantee that the control signal sent to the damper is not to generate energy, the control function is enabled only when the direction of the desired damping force and the error having the same direction. If the control function and the desired force have different sign, then the damper input voltage is set to zero. Mathematically, the continuous control strategy can be represented by [18]:
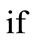
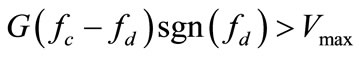
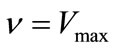
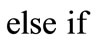
 (18)
(18)
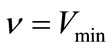
else

where
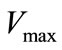 is the MR damper saturation voltage (2 volt),
is the MR damper saturation voltage (2 volt),
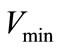 is the MR damper minimum voltage (zero volt),
is the MR damper minimum voltage (zero volt),
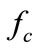 is the suspension desired damping force,
is the suspension desired damping force,
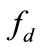 is the MR damper actual force,
is the MR damper actual force,
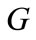 is a scaled gain.
is a scaled gain.
5. Results and Discussion
To evaluate the suspension system performance, the sprung mass acceleration, suspension working space (SWS) and dynamic tire load (DTL) of the quarter car model are considered as a ride comfort criteria. Based on a continuous variable damping methodology and sliding mode control using with ideal sky-hook model as a reference model, the simulation was carried out for two different excitations; the first is a road hump with peak amplitude of 0.1 m, and the second is a statistical random road. The
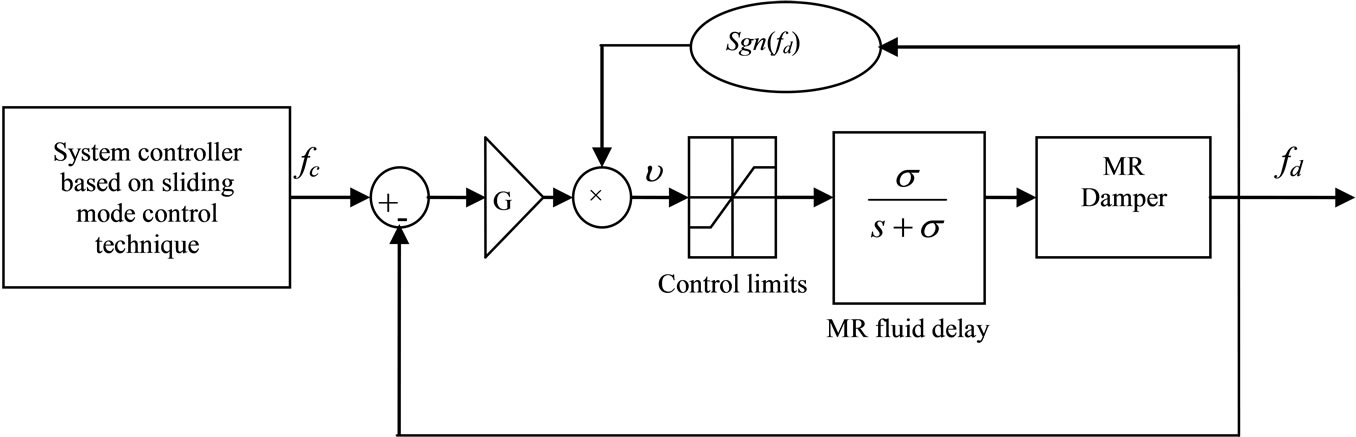
Figure 2. Block diagram for the MR damper controller.
MR damper scaling gains G is determined by a trial-and error and the other model parameters are adapted from Ref. [21] and given in Table 2. The sprung mass uncertainty (20% of the nominal sprung mass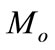 )
)  = 50 kg is used. All the simulation results include the MR damper passive cases (passive off is 0 V and passive on is 2 V). The generated results are compared with the optimal bi-linear passive damper with extension damping coefficient of 2444 Ns/m and compression damping coefficient of 500 Ns/m. The optimization for this passive damper has been carried using Genetic Algorithm (GA) [20]. All simulations are performed using Matlab/Simulink Software.
= 50 kg is used. All the simulation results include the MR damper passive cases (passive off is 0 V and passive on is 2 V). The generated results are compared with the optimal bi-linear passive damper with extension damping coefficient of 2444 Ns/m and compression damping coefficient of 500 Ns/m. The optimization for this passive damper has been carried using Genetic Algorithm (GA) [20]. All simulations are performed using Matlab/Simulink Software.
Figure 3 shows the system responses for the ride comfort criteria mentioned above with vehicle speed of 20 m/s over hump input with peak amplitude of 0.1 m, see Figure 3(a). As shown in Figures 3(b)-(d) there are significant improvements gained from the controlled MR damper for sprung mass acceleration, dynamic tyre load and suspension working space over the MR damper two passive cases and the optimal conventional passive suspension. Figure 3(e) shows the controlled voltage applied to the MR damper during the control processing. As shown it is not increased more than the maximum MR damper range (2 volt).
The statistical random road profile was described by its power spectral density (PSD) in frequency domain as [21];
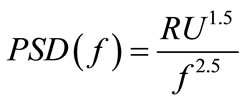 (19)
(19)
where R = 3.6 × 10−6 is the road roughness coefficient, U is the vehicle speed in m/s and f is the road excitation frequency in Hz. The road low cut-off frequency used in this simulation is 0.25 Hz and high cut-off frequency is 15 Hz. Using inverse fast Fourier transform, the PSD function, Equation (19) is transformed into time domain for 819.2 meter long and 4096 points, see Figure 4(a). Figure 4(b) shows the controllable MR damper force velocity behavior under random road excitation. As shown it takes an arbitrary value depending on the system re-

Table 2. Model parameters.
quirement and the designed controller. The results are generated in time domain and transformed into frequency domain using FFT transform in Matlab/Simulink software.
Figures 4(c)-(e) show the frequency response for the ride comfort criteria which are body acceleration, dynamic tyre load (DTL) and suspension working space (SWS). As we can notice from the figures the body acceleration and DTL for the controlled MR system are reduced compared to the other systems especially around the body mass resonance. However the passive MR damper shows a better result for SWS as compared to the other systems. This is due to its high voltage, on the case of passive-on with 2 Volt, causes more and more particle chains to be formed in the MR damper which make the damper stiffer then reduce the SWS. On other hand, the voltage applied to the controlled MR damper is less than 1.5 Volt, Figure 4(f). This means that the controlled MR damper has high vibration compensation with lower power consumption in comparison with the passive-on MR damper. For comparison with the other active systems, the root mean square (Rms) values for the random responses are calculated and compared with the following systems:
• Linear passive suspension system.
• Ideal sky-hook damper suspension system.
• Fully active suspension system.
Using same parameters, the ideal semi-active is de-signed based on optimal control using the continuous control strategy. The fully active suspension force is given by [21].

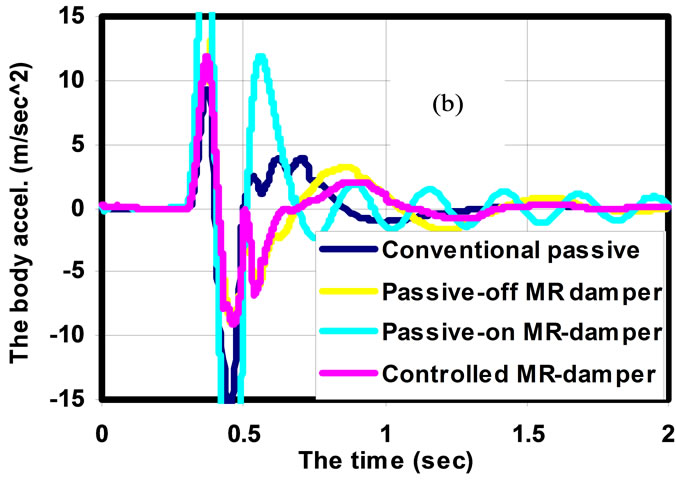

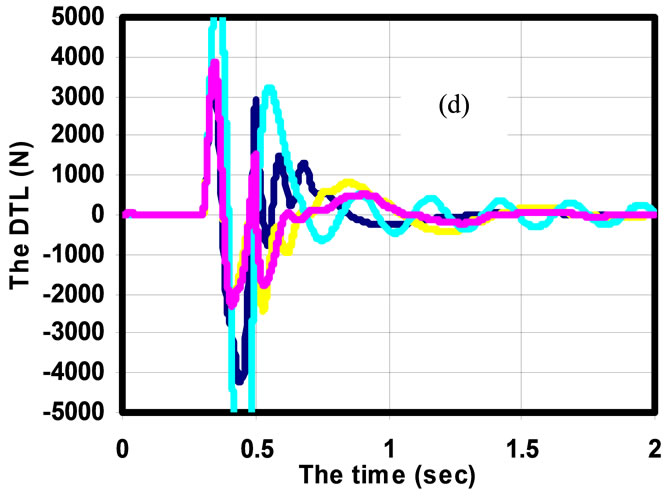
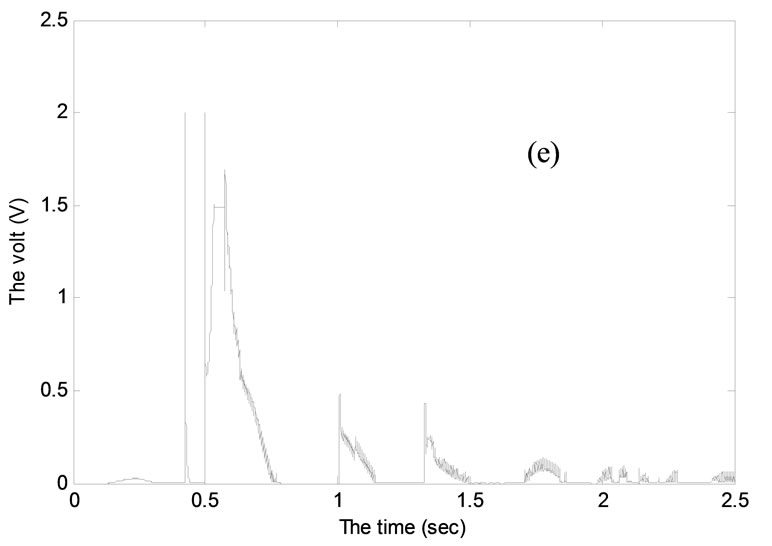
Figure 3. Quarter car model response for road hump input with speed of 20 m/s.
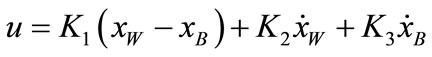 (20)
(20)
where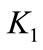 ,
, 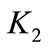 and
and 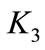 are feedback gains calculated based on LQR control technique and their values are 11,952, 636 and –2395 respectively. The first term of the right hand side of Equation (20) is represented by a passive spring for both semi-active and fully active while the other terms are generated by the sky-hook damper for the ideal semi-active suspension and by hydraulic actuator for fully active suspension system. More details for these systems are described in Refs. [20,21].
are feedback gains calculated based on LQR control technique and their values are 11,952, 636 and –2395 respectively. The first term of the right hand side of Equation (20) is represented by a passive spring for both semi-active and fully active while the other terms are generated by the sky-hook damper for the ideal semi-active suspension and by hydraulic actuator for fully active suspension system. More details for these systems are described in Refs. [20,21].
Figure 5 shows the performance envelope for the passive suspension system in comparison with the other systems controllable MR damper, fully active and ideal semi-active suspension systems. From this figure, it is noticed that by using the fully active and ideal semi-active systems based on LQR control technique, a high improvement in the ride comfort can be achieved at the expense of deterioration in the dynamic tyre load (road holding) compared to the passive suspension as well as controllable MR damper suspension systems. The controllable MR damper designed based on sliding mode control showed a significant improvement 24% and 22%
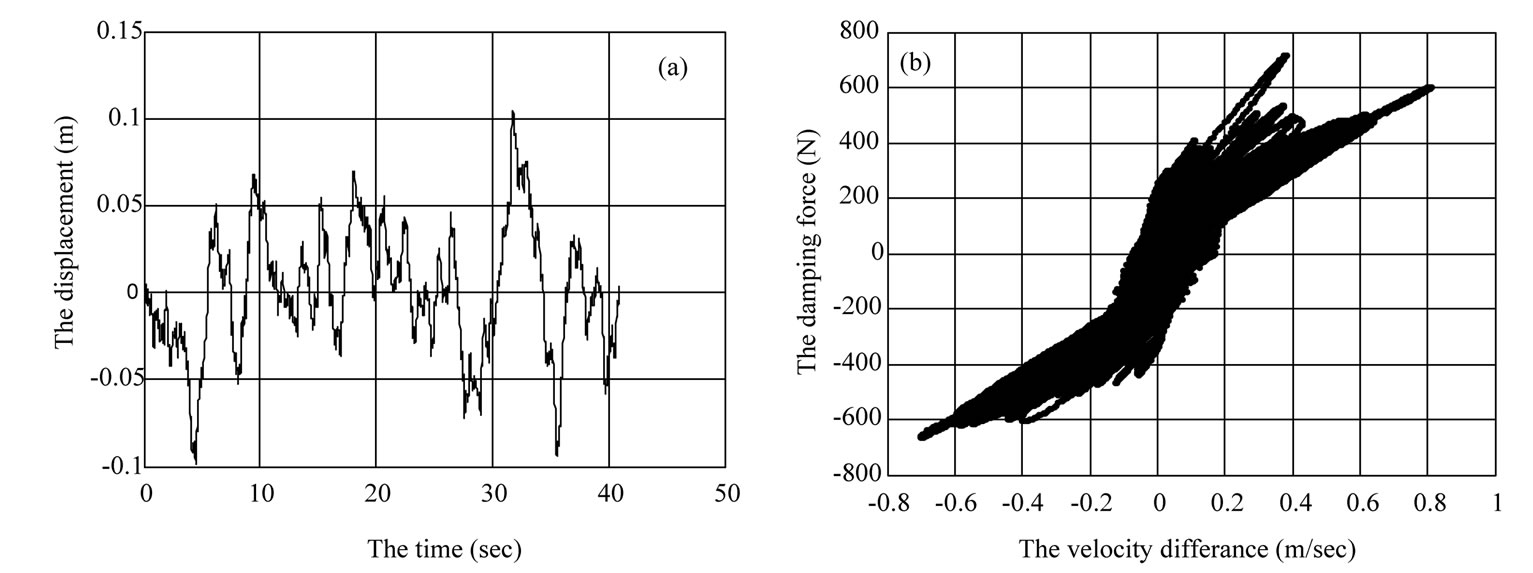
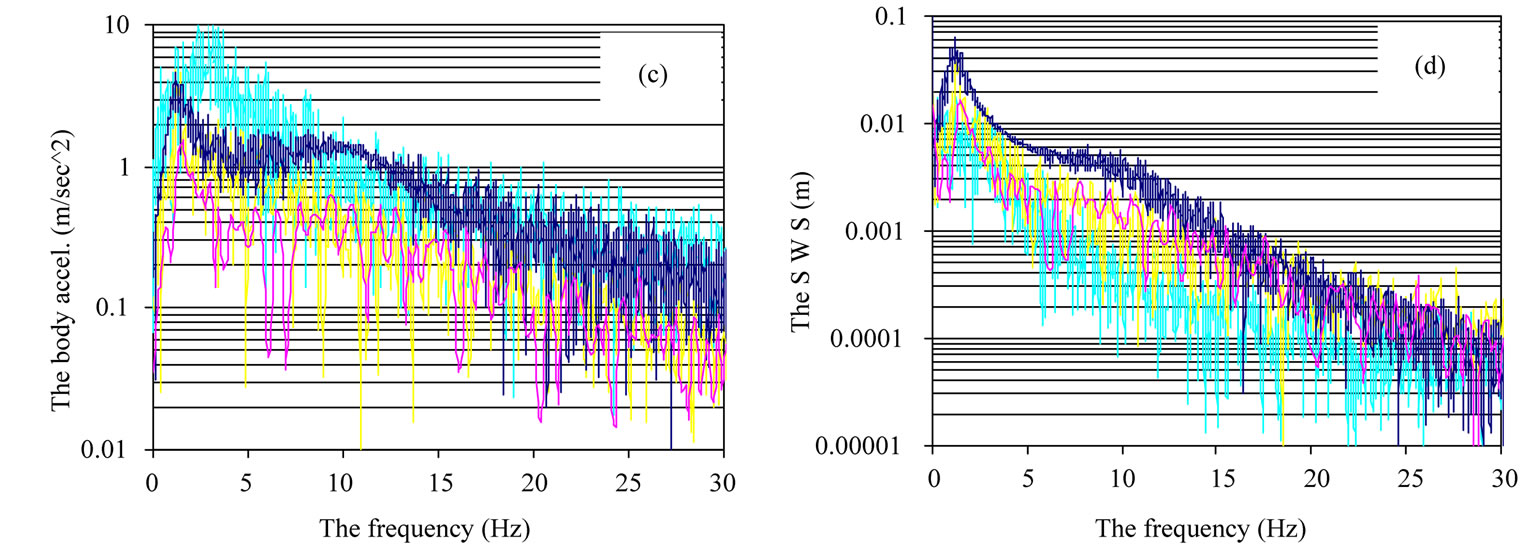
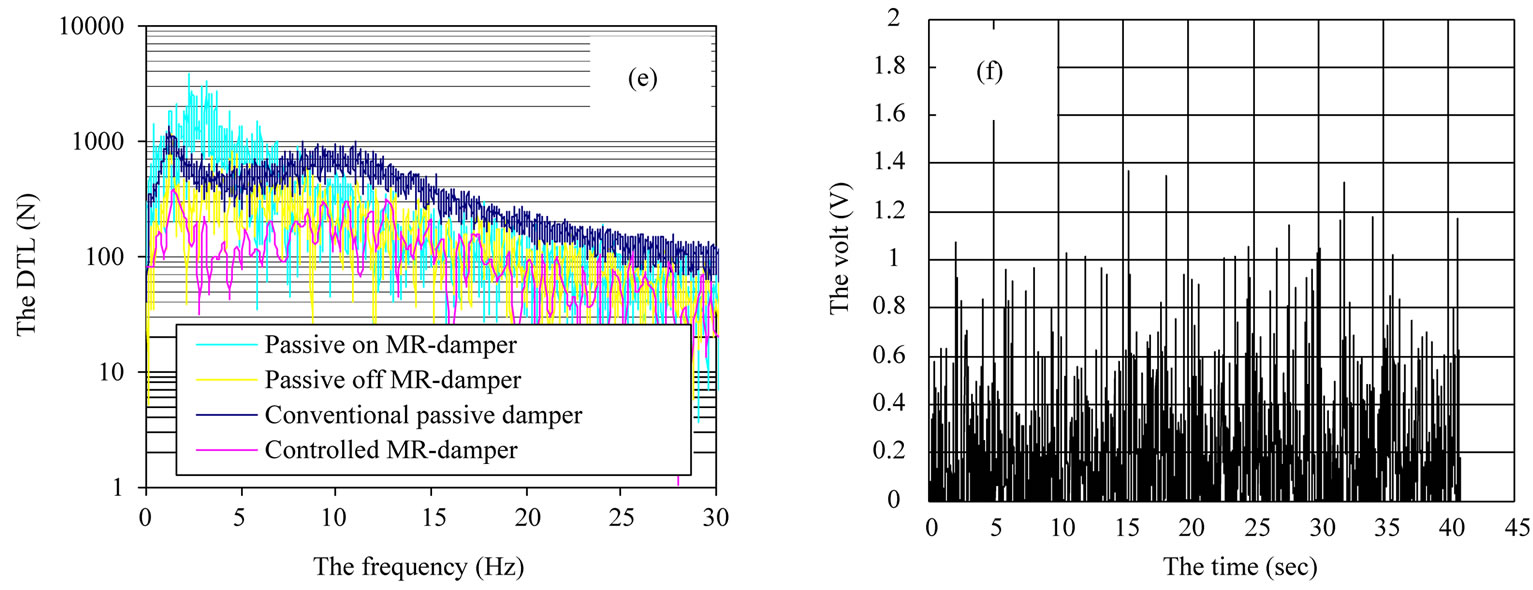
Figure 4. Frequency responses for quarter car ride comfort parameters using MR damper on random road with speed of 20 m/s.
on the road holding in comparison with fully active and ideal semi-active systems respectively. This means a good handling maneuver and enhanced vehicle lateral stability and safety. In other side, these improvements are highly promising from the point of view of road damage, so we can save the costs associated with repairing transportation infrastructure networks [22].
At similar Rms values of suspension working space, the controllable MR-damper is reduced the vehicle body acceleration by 6% over the conventional passive suspension. This reduction is very small in comparison with the ideal semi-active or fully active systems. However,

Figure 5. Ride comfort comparison between passive, ideal semi-active, fully active and controllable MR damper suspension systems based on Rms values for random excitation with vehicle speed of 20 m/s.
the fully active and ideal semi-active systems improved the vehicle body acceleration by 45% and 40% over the controlled MR damper. But these results are at the expense of road holding, which is related to vehicle stability, safety and traction performance. This problem was solved by introducing slow-active suspension systems. These systems have the advantages of fully active suspensions in the low frequency range i.e. 1 - 6 Hz and the above this frequency range the system working like the passive suspension. But still these slow-active systems are more complicated and power consumed in comparison with controllable dampers.
6. Conclusions
A quarter car suspension systems with MR damper has been investigated and compared with passive, fully active and ideal semi-active systems. For vehicle vibration control, a model-reference sliding mode controller has been used as a system controller and a continuous control strategy has been designed to adjust the MR damper control signal. The performances and characteristics of the car suspension system under two road excitations have been evaluated through computer simulation. Based on results achieved, the following conclusions have been drawn. For severe road hump input, the controllable MR damper has improved the transient responses for vehicle ride comfort performance criteria over the conventional passive suspension as well as the MR passive cases.
The results presented in this paper for the random input have shown that the controllable MR damper improves the vehicles road holding by 24% over fully active and 22% over ideal semi-active suspension systems. This means that the MR controllable damper with the given design has better lateral vehicle stability over the passive as well as all previous active suspension systems.
It was shown that the achieved improvements in the road holding for the controllable MR damper at the expense of vehicle body acceleration results, however only 6% reduction is achieved in comparison with the conventional passive suspension system. More effort is still required with the controllable MR damper controller through the control techniques to get a maximum benefits and compromise between the different vehicle dynamic modes.
The introduced design for the controllable MR damper is highly promising from the point of view of road damage, so we can save the costs associated with repairing transportation infrastructure networks.
REFERENCES
- J. Y. Wong, “Theory of Ground Vehicles,” 3rd Edition, Wiley-Inter Science, New York, 2001.
- D. Karnopp, “Active Damping in Road Vehicle Suspension Systems,” Journal of Vehicle System Dynamics, Vol. 12, No. 6, 1983, pp. 291-316. doi:10.1080/00423118308968758
- D. A. Crolla, G. R. Firth, P. J. Hine and P. T. Perarce, “The Performance of Suspensions Fitted with Controllable Dampers,” Journal of Vehicle System Dynamics, Vol. 20, 1991, pp. 149-165.
- S. M. El-Demardash, “Improvement of Trucks Ride Dynamics Using a Hydraulic Semi-Active Suspension System,” SAE Paper No 2002-01-3039, SP-1728, 2002.
- G. Alessanro, M. Mauro, S. Carla and U. Giampaolo, “Design of Predictive Semi-Active Suspension System,” Journal of Vehicle System Dynamics, Vol. 41, No. 4, 2004, pp. 277-300. doi:10.1080/00423110412331315169
- S. Tao, H. Zhenyu and C. Dayue, “Signal FrequencyBased Semi-Active Fuzzy Control for Two-Stage Vibration Isolation System,” Journal of Sound and Vibration, Vol. 280, No. 3-5, 2005, pp. 965-981.
- B. F. Spencer, S. J. Dyke, M. K. Sain and J. D. Carlson, “Phenomenological Model for Magnetorheological Dampers,” Journal of Engineering Mechanics, Vol. 123, No. 3, 1997, pp. 230-238. doi:10.1061/(ASCE)0733-9399(1997)123:3(230)
- Lord Corporation Web Site, 2004. http//www.lord.com
- C. C. Chang and L. Zhou, “Neural Network Emulation of Inverse Dynamics for a Magnetorheological Damper,” Journal of Structural Engineering, Vol. 128, No. 2, 2002, pp. 231-239. doi:10.1061/(ASCE)0733-9445(2002)128:2(231)
- K. C. Schurter and P. N. Roschke, “Fuzzy Modeling of a Magnetorheological Damper Using ANFIS,” Proceedings of the IEEE International Conference on Fuzzy Systems, Vol. 1, 2000, pp. 122-127.
- S. B. Choi, S. K. Lee and Y. P. Park, “A Hysteresis Model for the Field-Dependent Damping Force of a Magnetorheological Damper,” Journal of Sound and Vibration, Vol. 245, No. 2, 2001, pp. 375-383. doi:10.1006/jsvi.2000.3539
- G. Jin, M. K. Sain, K. D. Pham, B. F. Spencer and J. C. Ramallo, “Modeling MR-Dampers: A Nonlinear Blackbox Approach,” Proceedings of the American Control Conference, Vol. 1, 2001, pp. 429-434.
- A. Leva and L. Piroddi, “NARX-Based Technique for the Modelling of Magneto-Rheological Damping Devices,” Smart Materials and Structures, Vol. 11, No. 1, 2002, pp. 79-88. doi:10.1088/0964-1726/11/1/309
- H. H. Tsang, R. K. L. Su and A. M. Chandler, “Simplified Inverse Dynamics Models for MR Fluid Dampers,” Engineering Structures, Vol. 28, No. 3, 2006, pp. 327- 341. doi:10.1016/j.engstruct.2005.06.013
- S. Xubin, A. Mehdi, S. Southward and L. Miller, “Paramettric Study of Nonlinear adaptive Control Algorithm with Magneto-Rheological Suspension Systems,” Communications in Nonlinear Science and Numerical Simulation, Vol. 12, No. 4, 2007, pp. 584-607. doi:10.1016/j.cnsns.2005.05.004
- N. M. Kwok, Q. P. Ha, M. T. Nguyen, J. Li and B. Samali, “Bouc-Wen Model Parameter Identification for a MR Fluid Damper Using Computationally Efficient GA,” ISA Transactions, Vol. 46, No. 2, 2007, pp. 167-179. doi:10.1016/j.isatra.2006.08.005
- W. H. Liao and C. Y. Lai, “Vibration Control of a Suspension System via a Magnetorheological Fluid Damper,” Journal of Vibration and Control, Vol. 8, No. 4, 2002, pp. 527-547. doi:10.1177/107754602023712
- A. H.-F. Lam and W.-H. Lio, “Semi-Active Control of Automotive Suspension Systems with Magnetorheological Dampers,” International Journal of Vehicle Design, Vol. 33, No. 1-3, 2002, pp. 50-75.
- E. J. Slotine and W. Li, “Applied Nonlinear Control,” Prentice-Hall, New Jersey, 1991, pp. 276-310.
- M. El-Kafafy, “Vehicle Vibration Control Using Smart Fluid Dampers,” MSc Thesis, Helwan University, Egypt, 2006.
- M. El-Kafafy, E. Rabeih, S. El-Demerdash and A. El-Butch, “Active Suspension Design for Passenger Cars Using LQR and GA with PID Controller,” SAE Technical Paper No. 2007-01-2423, 2007.
- S. Lu, C. Ximing and Y. Jun, “Genetic Algorithm-Based Optimum Vehicle Suspension Design Using Minimum Dynamic Pavement Load as a Design Criteria,” Journal of Sound and Vibration, Vol. 301, 2007, pp. 18-27. doi:10.1016/j.jsv.2006.08.040




