Engineering
Vol. 3 No. 4 (2011) , Article ID: 4590 , 4 pages DOI:10.4236/eng.2011.34036
Probability Analysis for the Damage of Gravity Dam
1School of Civil and Hydraulic Eng., Dalian University of Technology, Dalian, China
2State Key Lab. of Coastal and Offshore Eng., Dalian University of Technology, Dalian, China
E-mail: xuqiang528826@163.com, eerd001@dlut.edu.cn
Received November 22, 2010; revised January 11, 2011; accepted March 8, 2011
Keywords: Gravity dam, Damage, Probability Analysis, Pseudo excitation method, Mazar damage model, Response surface method
ABSTRACT
Damage reliability analysis is an emerging field of structural engineering which is very significant in structures of great importance like arch dams, large concrete gravity dams etc. The research objective is to design and construct an improved method for damage reliability analysis for concrete gravity dam. Firstly, pseudo excitation method and Mazar damage model were used to analyze how to calculate damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus was deterministic. Moreover, response surface method was improved from the aspects of the regression of sample points, the selection of experimental points, the determined method of weight matrix and the calculation method of checking point respectively. Then, the above method was used to analyze guarantee rate of damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus was random. Finally, a test example was given to verify and analyze the convergence and stability of this method. Compared with other conventional algorithm, this method has some strong points: this algorithm has good convergence and stability and greatly enhances calculation efficiency and the storage efficiency. From what has been analyzed, we find that damage expected value is insensitive to the randomness of initial elastic modulus so we can neglect the randomness of initial elastic modulus in some extent when we calculate damage expected value.
1. Introduction
The theory and methods of reliability analysis have been developed significantly during the last twenty years and have been documented in an increasing number of publications. These improvements in structure reliability theory and the attainment of more accurate quantification of the uncertainties associated with structural loads and resistances have stimulated the interest in the structure reliability analysis. Although from a theoretical point of view the field has reached a stage where the developed methodologies are becoming widespread, the quantitative assessment and classification of the reliability is still a complex and difficult task. In order to assess the reliability, a rigorous series of tests has to be carried out.
As early as 1986, Ross B. Corotis [1] developed the analysis of effects of parameter uncertainty on the response of vibratory systems to random excitation. Benaroya H, Rehak M [2] and Spanos PD, Ghanem RG [3] extended the stochastic finite element method (SFEM) to incorporate the uncertainties in structural parameters. Leger [4] presented guidelines for dam-safety assessment based on the gravity method. Compared with the rigidbody limiting equilibrium method, the FEM used in the calculation of deep anti-sliding measures did not require the assumption of any slide plane. Wang Fei-yue and Xu Zhi-sheng [5] studied the stability of tailing dams. Their studies showed that both the fuzziness and the randomness of dam failure need to be considered. A comprehensive review of studies on fuzzy reliability was presented by Ross Reinhard Viert [6], who combined fuzzy set theory and reliability research to evaluate the risk in civil engineers. Motivated by the development of various reliability theories, Enrique Castillo and Carmen Castillo [7] gave the main results that allowed a sensitivity analysis to be performed in a general optimization problem, including sensitivities of the objective function, the primal and the dual variables with respect to data. Using a numerical procedure, Junho Song and Won-Hee Kang [8] proposed matrix-based system reliability (MSR) method to compute the probabilities of general system events efficiently by simple matrix operations. KwaiSang Chin and Ying-Ming Wang [9] used failure mode and effects analysis (FMEA) to evaluate a system for possible ways in which failures could occur.
The basic purpose of structural reliability analysis is to obtain the probabilistic responses of structural systems with uncertain design parameters, such as loadings, material parameters (strength, elastic modulus, Poisson's ratio, etc.), and shape dimensions. Among the methods available for such problems, the response surface method is a powerful tool [10]. The response surface method, was originally proposed by Box and Wilson [11] as a statistical tool, to find the operating conditions of a chemical process at which some response was optimized. Subsequent generalizations developed this method. Khuri, Cornell [12] and Myers, Montgomery [13] all introduced the response surface method in their books. Wong [14,15] and Faravelli [16,17] and Jiang [18] improved the method to fit the indeterminate coefficients of response surface. Bucher [19] and Rajashekhar [20] researched the convergence and stability of the response surface method. Guan [21] evaluated the effect of response surface parameter variation on structural reliability. Gupta [22] used the response surface method to study the extremes of Von Mises stress in nonlinear structures under Gaussian excitations.
However, until now, most of reliability methods such as the first order reliability method (FORM) [23], the second-order reliability method (SORM) [24-27], weighted regression method (WRM) and space reduced weighted regression method (SRWRM) [28] can not be used to analyze large structure, because the traditional reliability methods have two aspects of deficiencies: On the one hand, limited state function is usually implicit when we use finite element method (FEM) to analyze structure. It leads to that the implicit limited state function’ partial derivatives for basic random variables are difficult to obtain. On the other hand, in order to overcome the above defects, some reliability methods use polynomial response surface function to fit implicit limited state function, but the number of basic random variables is very big when we analyze large structure. And these reliability methods need more experimental points to confirm the indeterminate coefficients of these basic random variables. It leads to that, during the process, the calculation efficiency and the storage efficiency of these methods are very low. Even, in some large structure, it is impossible to obtain such many experimental points. Therefore, most of reliability methods only can be used to analyze small structures but inability to large structure.
Furthermore, when traditional methods analyze the damage of gravity dam, the seismic load is considered to deterministic acceleration time course. But, in fact, the acceleration time courses of seismic load are different although they have the same power spectrum density. So the traditional method ignores the randomness of seismic load. In addition, most of traditional probability analysis methods only consider the randomness of load but not consider the randomness of parameters of model at the same time. So these methods for gravity dam probability analysis are not complete.
In this paper, we analyze not only the randomness of load but also the randomness of parameters of gravity dam model for the influence of tension damage factor of elements in gravity dam model. The research route of this paper is as follow: to begin with, based on pseudo excitation method and Mazar damage model, we calculate damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus is deterministic. In addition, we establish the improved response surface method based on weighted regression which can be used to analyze large structure. And then we use this method to analyze guarantee rate of damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus is random. Finally, we give a test example to verify and analyze the convergence and stability of this paper’s method.
2. Probabilistic Approach to Evaluate Gravity Dam Damage Excited by Random Seismic Load and Deterministic Static Load under the Condition of Deterministic Initial Elastic Modulus
The seismic load is considered to deterministic acceleration time course when we analyze the damage of gravity dam by the conventional method. However, in fact, the acceleration time courses of seismic load are different although they have the same power spectrum density. So the conventional method ignores the randomness of seismic load. In the method of this paper, we analyze the randomness of seismic load directly from power spectrum density.
Firstly, we analyze the element strains of dam model excited by deterministic static load. These element strains are considered to the expected value 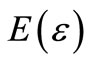 of element strains.
of element strains.
Then, we begin to analyze square variance 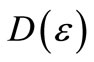 of element strains.
of element strains.
According to the vibration equation of gravity dam multi-degree-of-freedom system, we have
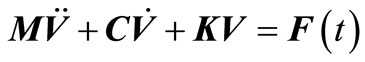 (1)
(1)
where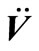 ,
, 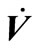 and
and 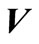 are acceleration, velocity and displacement of nodes in dam model, respectively;
are acceleration, velocity and displacement of nodes in dam model, respectively;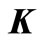 ,
, 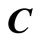 and
and 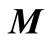 are stiffness matrix, damping matrix and mass matrix of dam model, respectively.
are stiffness matrix, damping matrix and mass matrix of dam model, respectively.
By mode-superposition method, set seismic load is non-stationary process 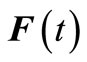 as
as
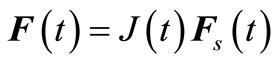 (2)
(2)
where 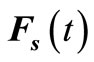 and
and  are stationary process and time envelope curve, respectively.
are stationary process and time envelope curve, respectively.
According to pseudo excitation method, construct virtual force as
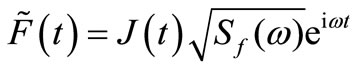 (3)
(3)
where 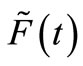 and
and 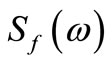 are virtual force and power spectrum density of stationary process
are virtual force and power spectrum density of stationary process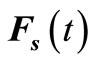 , respectively.
, respectively.
Substituting (3) into (1) and we have
 (4)
(4)
where 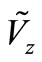 and
and 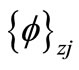 are fictive motion response and j vibration mode value of node z, respectively;
are fictive motion response and j vibration mode value of node z, respectively;
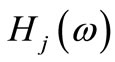 and
and  are frequency response function and mode shape participation coefficient, respectively.
are frequency response function and mode shape participation coefficient, respectively.
And we can obtain 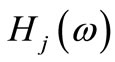 from (1).
from (1).
Based on random vibration theory, we have
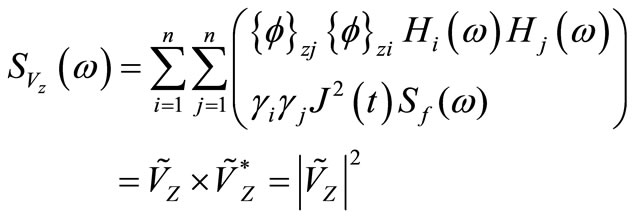 (5)
(5)
where 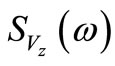 is power spectrum density of displacement response of node z Through (5), we have
is power spectrum density of displacement response of node z Through (5), we have
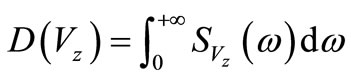 (6)
(6)
Give the strain of element q as
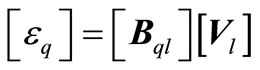 (7)
(7)
where 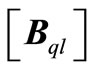 and
and 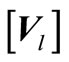 are strain matrix of element q and displacement vector of nodes in element q.
are strain matrix of element q and displacement vector of nodes in element q.
So we can write the square variance 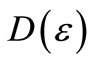 of element strains as
of element strains as
 (8)
(8)
Through assuming element strains obey normal distribution, we can obtain probability distribution of element strains.
Regard Mazar damage model which is only related to strain as damage constitutive equation of concrete and write the tension damage factor of element as
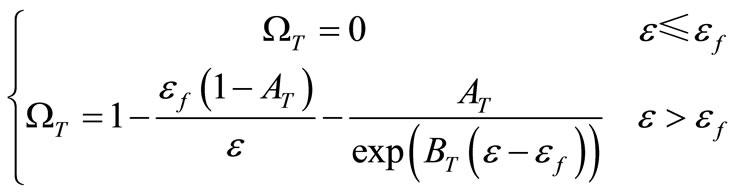 (9)
(9)
where 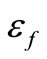 is damage threshold and 0.7 ≤AT ≤ 1, 104 ≤ BT ≤ 105, 0.5 × 10−4 ≤
is damage threshold and 0.7 ≤AT ≤ 1, 104 ≤ BT ≤ 105, 0.5 × 10−4 ≤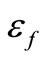 ≤ 1.5 × 10−4.
≤ 1.5 × 10−4.
In which, we only consider element strain at x direction and give the tension damage expected value through probability distribution of element strains and the tension damage factor of element as
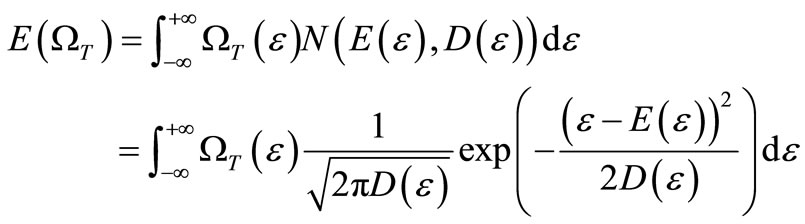 (10)
(10)
where 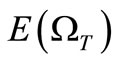 and
and 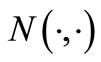 are tension damage expected value and normal distribution function, respectively.
are tension damage expected value and normal distribution function, respectively.
Substituting (10) into (11) and we have
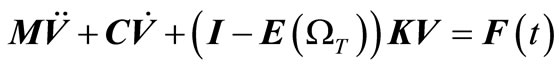 (11)
(11)
where 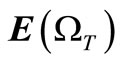 and
and 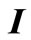 are tension damage expected value matrix and unit matrix, respectively.
are tension damage expected value matrix and unit matrix, respectively.
We repeat the above steps until reaching a certain convergence criteria. Then we can obtain the iterative process of expected value 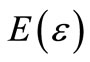 and square variance
and square variance 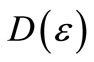 of element strains. And finally we can obtain tension damage expected value matrix
of element strains. And finally we can obtain tension damage expected value matrix .
.
3. Probabilistic Approach to Evaluate Gravity Dam Damage Excited by Random Seismic Load and Deterministic Static Load under the Condition of Random Initial Elastic Modulus
We have analyzed the randomness of load. Then we consider the randomness of initial elastic modulus. In this part, we improve response surface method based on weighted regression and make this method can be used in large structure such as gravity dam. It shows that the algorithm has good convergence and stability and greatly enhances calculation efficiency and the storage efficiency compared with other conventional algorithm.
3.1. Implicit Limited State Function 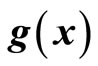 Setting
Setting
We write implicit limited state function 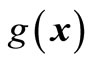 as
as
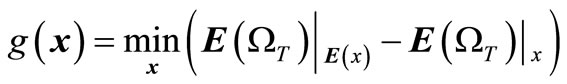 (12)
(12)
where 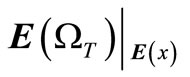 and
and 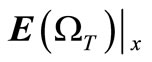 are tension damage expected value matrix under the condition of deterministic and random initial elastic modulus, respectively.
are tension damage expected value matrix under the condition of deterministic and random initial elastic modulus, respectively.
And 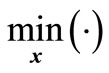 is the minimum value of matrix elements.
is the minimum value of matrix elements.
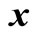 is basic random variables vector (in this paper, the basic random variables are random initial elastic modulus of elements of gravity dam model)
is basic random variables vector (in this paper, the basic random variables are random initial elastic modulus of elements of gravity dam model)
3.2. The Establishment of Improved Response Surface Method Based on Weighted Regression
Use second-order polynomial response surface function 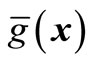 to fit implicit limited state function
to fit implicit limited state function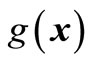 , we have
, we have
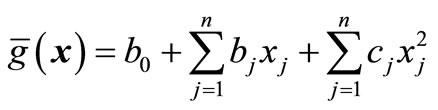 (13)
(13)
where 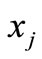 and
and 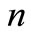 are basic random variables and the number of basic random variables, respectively;
are basic random variables and the number of basic random variables, respectively;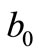 ,
, 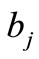 and
and 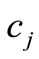 are indeterminate coefficients.
are indeterminate coefficients.
However, the number of basic random variables is very big when we analyze large structure. It is impossible to obtain the indeterminate coefficients by the traditional response surface method because we can only obtain m sample points which can not reach the number 2n + 1 to fit second-order polynomial response surface function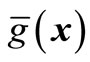 . Thus, we try to use second-order polynomial response surface function
. Thus, we try to use second-order polynomial response surface function 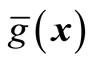 to best approximate implicit limited state function
to best approximate implicit limited state function 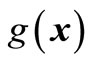 by m sample points.
by m sample points.
Select m (m < 2n + 1) experimental points 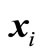 (i = 1, 2, ···, m), and calculate implicit limit state function value
(i = 1, 2, ···, m), and calculate implicit limit state function value 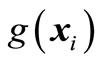 which corresponds to the experimental points
which corresponds to the experimental points 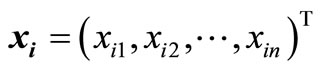 , and then obtain the sample vector
, and then obtain the sample vector  .
.
Set  as the solution vector which is to be determined, and use m experimental points
as the solution vector which is to be determined, and use m experimental points 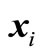 to compose experimental matrix
to compose experimental matrix 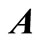 as
as
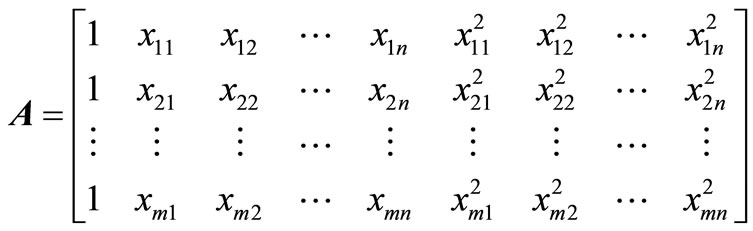 (14)
(14)
By singular value decomposition of experimental matrix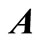 , we have
, we have
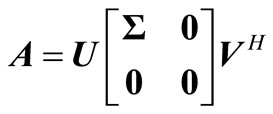 (15)
(15)
where 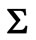 is m × m diagonal matrix;
is m × m diagonal matrix; 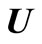 and
and 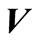 are morder and (2n + 1) -order unitary matrix, respectively.
are morder and (2n + 1) -order unitary matrix, respectively.
Give the solution vector 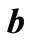 as
as
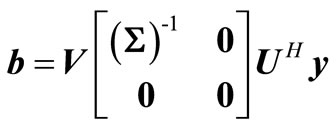 (16)
(16)
Set weight matrix  is m × m diagonal matrix which gives m experimental points
is m × m diagonal matrix which gives m experimental points  weight value.
weight value.
 (17)
(17)
Rewrite the solution vector  as
as
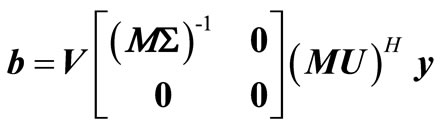
3.3. The Establishment of Weight Matrix 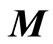
We want to achieve two goals when using second-order polynomial response surface function 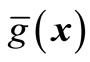 to approximate implicit limited state function
to approximate implicit limited state function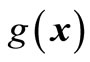 . The first goal is that we want the value of implicit limited state function
. The first goal is that we want the value of implicit limited state function 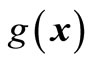 to be zero. The second goal is that we want to approximate implicit limited state function
to be zero. The second goal is that we want to approximate implicit limited state function  around checking point
around checking point . Thus, we establish weight matrix
. Thus, we establish weight matrix 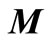 as
as
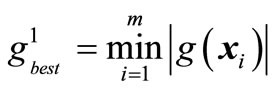 (19)
(19)
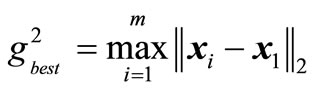 (20)
(20)
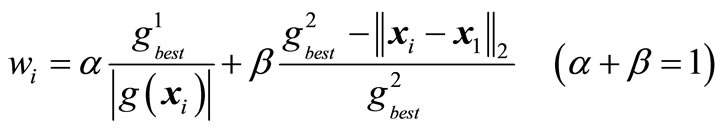 (21)
(21)
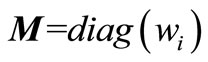 (22)
(22)
where  is center point.
is center point.
3.4. The m Experimental Points  Selection in the Initial Iterative Step
Selection in the Initial Iterative Step
In the initial iterative step, we select m experimental points 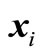 as
as
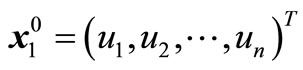 (23)
(23)
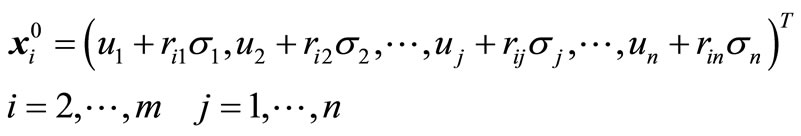 (24)
(24)
where 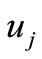 and
and 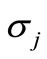 are expected value and mean square deviation of basic random variables
are expected value and mean square deviation of basic random variables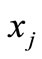 , respectively;
, respectively; 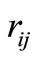 is random number in the interval
is random number in the interval 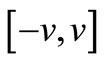 where
where 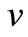 is deviation factor.
is deviation factor.
3.5. Deviation Factor Adjusting
Deviation factor has an influence on convergence speed in iterative procedure. Thus, in order to improve convergence speed, we adjust deviation factor in each iterative step as
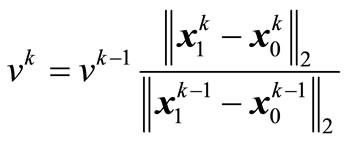 (25)
(25)
where 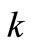 is the iterative step number.
is the iterative step number.
3.6. Calculation Method of Checking Point 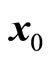
Derivation calculus to second-order polynomial response surface function 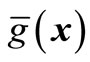 is complex. Thus, we adopt improved method based on Lagrange multiplier rule as follow.
is complex. Thus, we adopt improved method based on Lagrange multiplier rule as follow.
We can obtain the design checking point 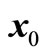 through solving the constrained optimization problem (26) as
through solving the constrained optimization problem (26) as
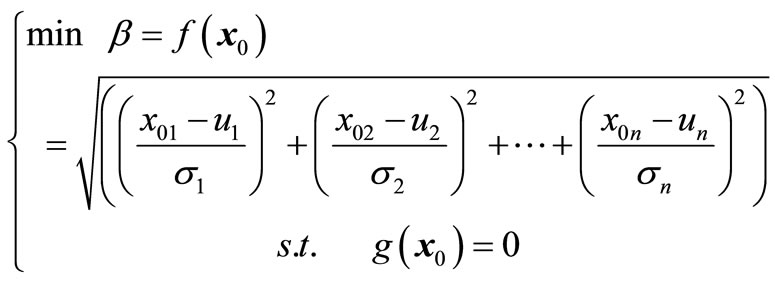 (26)
(26)
where 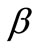 is reliability index.
is reliability index.
Substitute (13) into the constrained optimization problem (26) and rewrite constrained optimization problem (27) as
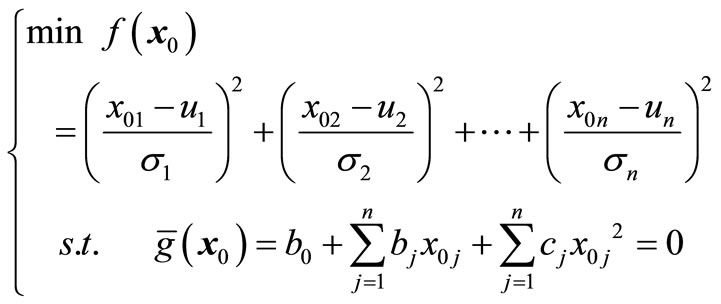 (27)
(27)
Based on Lagrange multiplier rule, we can rewrite the constrained optimization problem (27) as
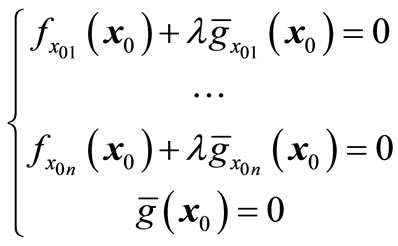 (28)
(28)
Unfold (28) as
 (29)
(29)
Solve (29) as
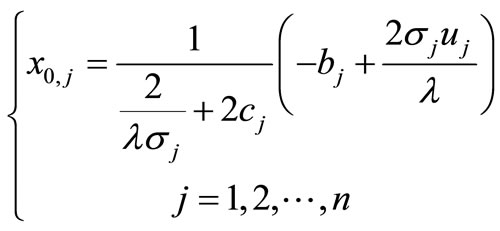 (30)
(30)
From (29) and (30), we find the second-order polynomial 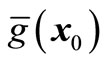 is the single-variable λ function. Thus we have
is the single-variable λ function. Thus we have
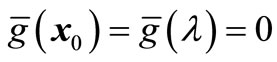 (31)
(31)
By Binary Search, we can solve (31) as follow:
First step: Taking two values λ1, λ2 to fit the conditions 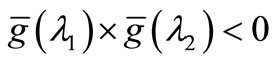 , and making
, and making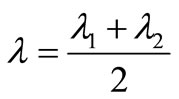 .
.
Second step: When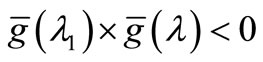 , making λ2 = λ and
, making λ2 = λ and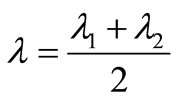 .
.
Third step: When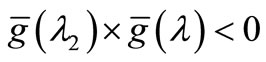 , making λ1 = λ and
, making λ1 = λ and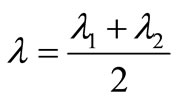 .
.
Through above iterative process, we can obtain the value of the variable λ. Substituting λ into (30), we can obtain the value of the design checking point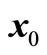 .
.
3.7. The Basic Steps of Improved Response Surface Method Based on Weighted Regression
The basic steps of improved response surface method based on weighted regression are as follow:
First step: in k iterative step, we obtain m experimental points 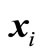 through (23), (24). We calculate implicit limit state function value
through (23), (24). We calculate implicit limit state function value 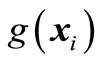 which corresponds to the experimental points
which corresponds to the experimental points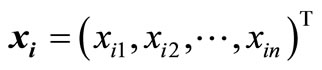 , and then obtain the sample vector
, and then obtain the sample vector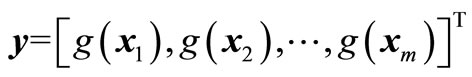 . We obtain weight matrix
. We obtain weight matrix 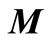 by (19-22), and then obtain solution vector
by (19-22), and then obtain solution vector 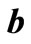 by .
by .
Second step: We obtain checking point 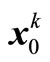 by improved method based on Lagrange multiplier rule, and then we calculate center point
by improved method based on Lagrange multiplier rule, and then we calculate center point 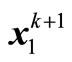 at next iterative step as
at next iterative step as
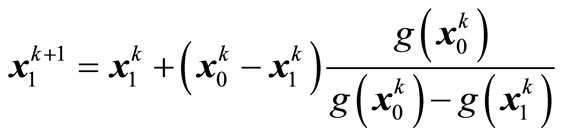 (32)
(32)
Third step: We obtain deviation factor 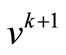 by (25) and obtain m experimental points
by (25) and obtain m experimental points 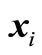 through (23), (24). If reliability index
through (23), (24). If reliability index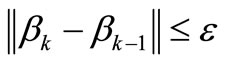 , we stop iterative procedure. If reliability index
, we stop iterative procedure. If reliability index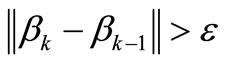 , we return the first step.
, we return the first step.
3.8. Numerical Example
We give a numerical example in order to verify and analyze the convergence and stability of this method.
Set implicit limited state function 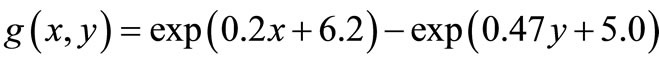 where basic random variables
where basic random variables 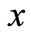 and
and 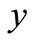 obey standard normal distribution and
obey standard normal distribution and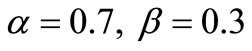 . We use 2 experimental points in this paper’s method compared with 3-5 experimental points in other conventional algorithm. We obtain the comparison result when using the same initial deviation factor
. We use 2 experimental points in this paper’s method compared with 3-5 experimental points in other conventional algorithm. We obtain the comparison result when using the same initial deviation factor 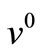 as Table 1 [19]. We obtain the iterative process when initial deviation factor
as Table 1 [19]. We obtain the iterative process when initial deviation factor 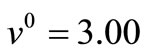 as Table 2.
as Table 2.
From Table 1 and Table 2, we can obtain the conclusion that this algorithm has good convergence and stability and greatly enhances calculation efficiency and the storage efficiency compared with other conventional algorithm.
4. Numerical Analysis of Gravity Dam Model
The gravity dam is 160 m high. The normal pool level (NPL) is 155 m deep. The level of back of dam is 10 m deep. The elevation of upstream and downstream broken-line sloping surface relative to foundation plane are 80 m and 140 m respectively. The concrete strength of gravity dam is C20. The finite element model of the gravity dam is divided into 2432 elements. The model consisted of 8-node iso parametric plane elements for the dam and foundation. The density of dam is 2450 kg/m3, and Poisson ratio λ = 0.18. The initial elastic modulus of dam E = 3.50 Gpa. The density of rock foundation is 2700 kg/m3, and Poisson ratio is 0.25.The initial elastic modulus of rock foundation E = 4.00 Gpa. And parame-
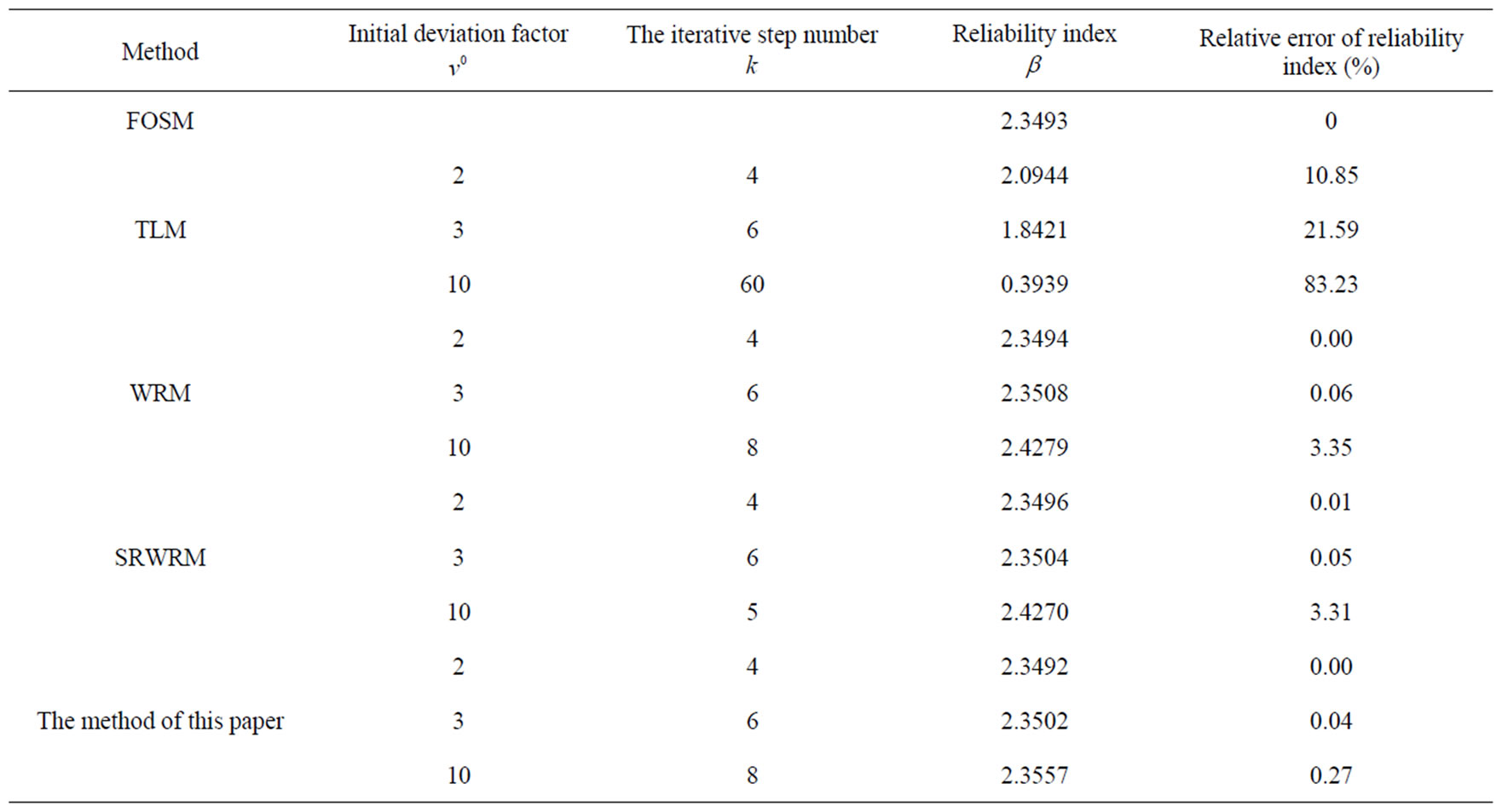
Table 1. Final result of example.
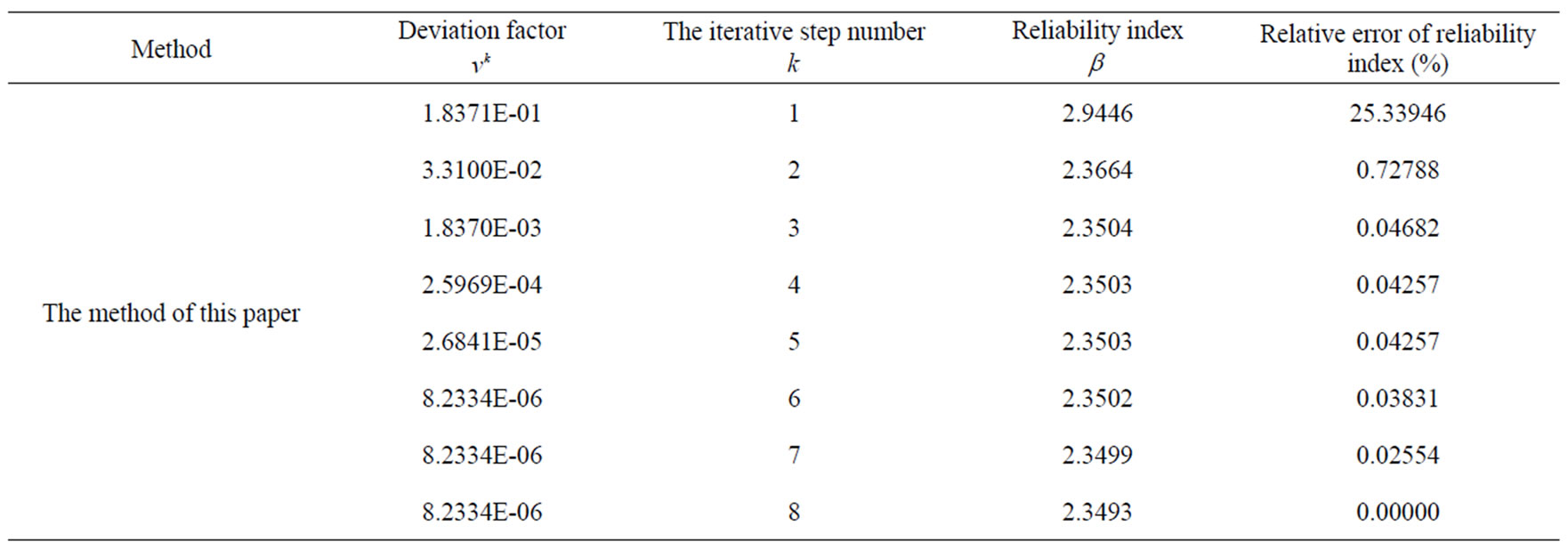
Table 2. Iterative procedure of example (initial deviation factor = 3).
ters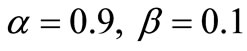 .
.
Deterministic static load includes gravity load and hydro static and uplift pressure while random load includes seismic load. The power spectrum density of seismic load is given as
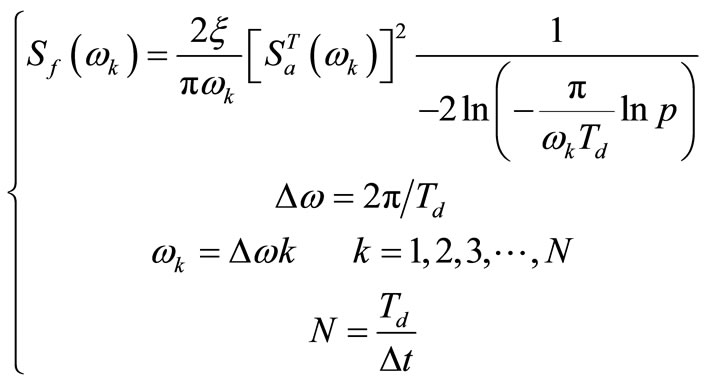 (33)
(33)
where 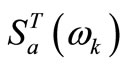 and
and  are target response spectrum and damping ratio, respectively; p (p ≤ 0.15)and
are target response spectrum and damping ratio, respectively; p (p ≤ 0.15)and 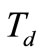 are exceeding response spectrum probability and duration of ground motion, respectively;
are exceeding response spectrum probability and duration of ground motion, respectively; 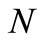 and
and 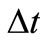 are the number of trigonometric series and time step, respectively.
are the number of trigonometric series and time step, respectively.
The dam model is shown in Figure 1. The probability distributions of all random parameters of each element are shown in Table 3. And the expected values of tension damage factors of each element are shown in Figure 2. The reliability index, guarantee rate about damage expected value and deviation factor under the condition of random initial elastic modulus iterative procedure are shown in Figure 3, Figure 4 and Figure 5. The values of Figure 3, Figure 4 and Figure 5 are shown in Table 4.
In each iterative step of the method of this paper, we use only 10 experimental points to approximate implicit limited state function  while the traditional response surface method needs 4865 experimental points. So the method of this paper saves large storage space and can be accepted in analyzing large structure such as gravity dam.
while the traditional response surface method needs 4865 experimental points. So the method of this paper saves large storage space and can be accepted in analyzing large structure such as gravity dam.
From what has been analyzed above, we have the conclusion that the damage locations of gravity dam are jetty
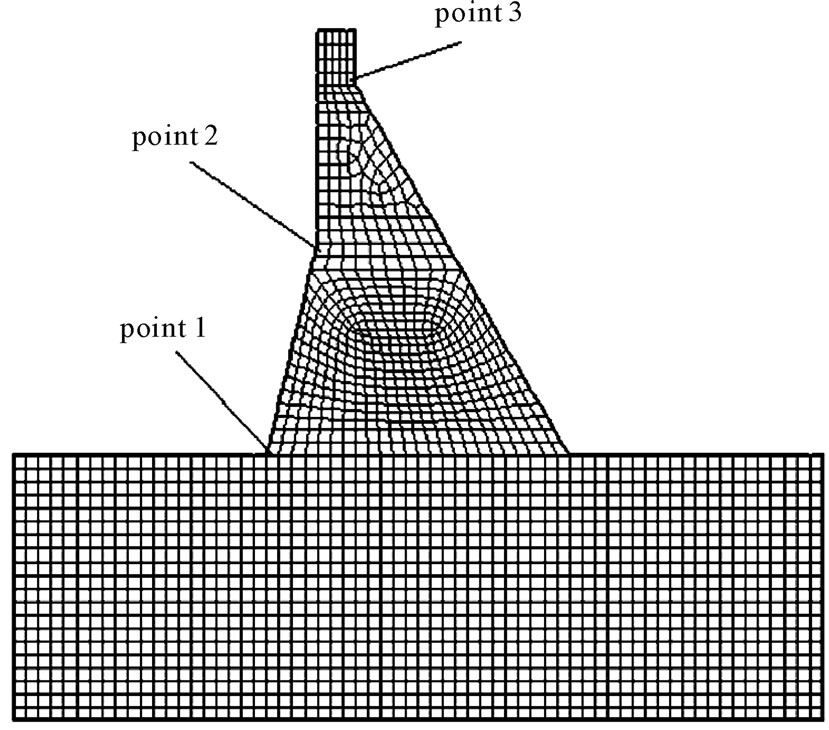
Figure 1. Gravity dam model.
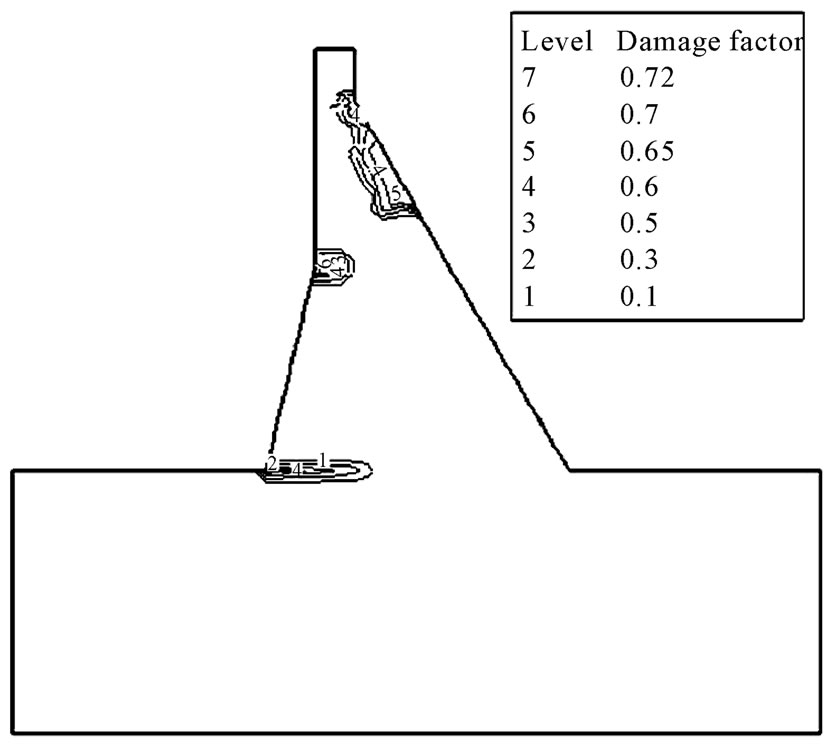
Figure 2. Damage contour map of gravity dam model.
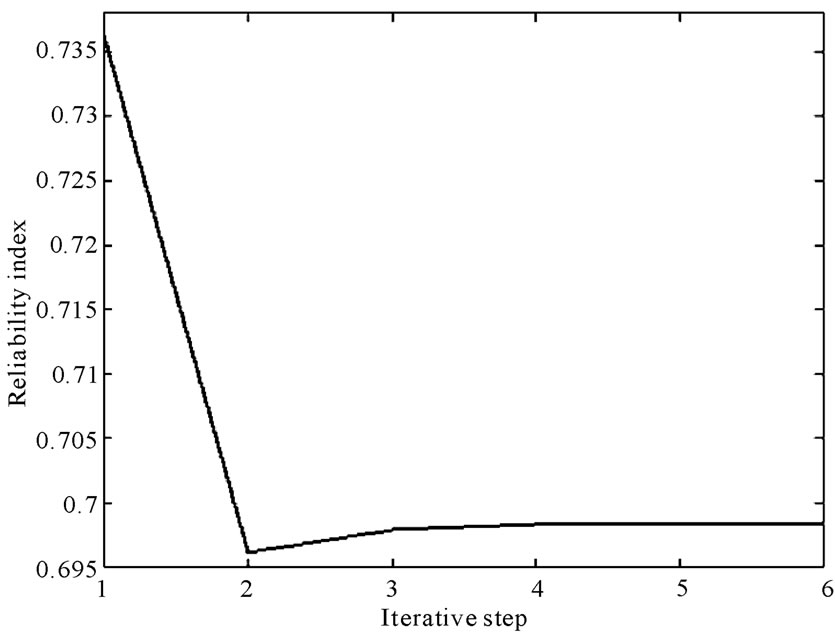
Figure 3. Reliability index iterative procedure.
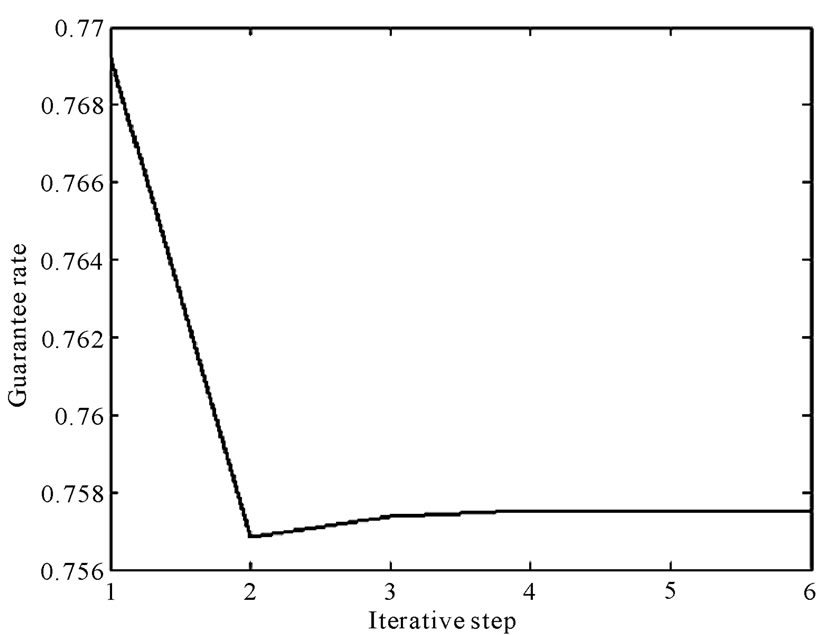
Figure 4. Guarantee rate iterative procedure about damage expected value.
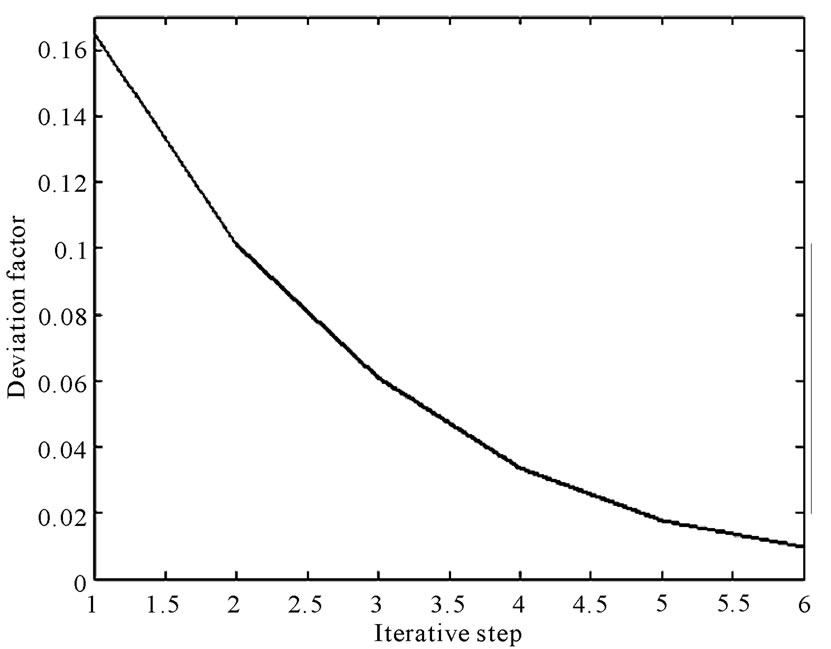
Figure 5. Deviation factor iterative procedure.
head and the heel of gravity dam so we should strengthen these locations above. From Figure 3, we have the con-
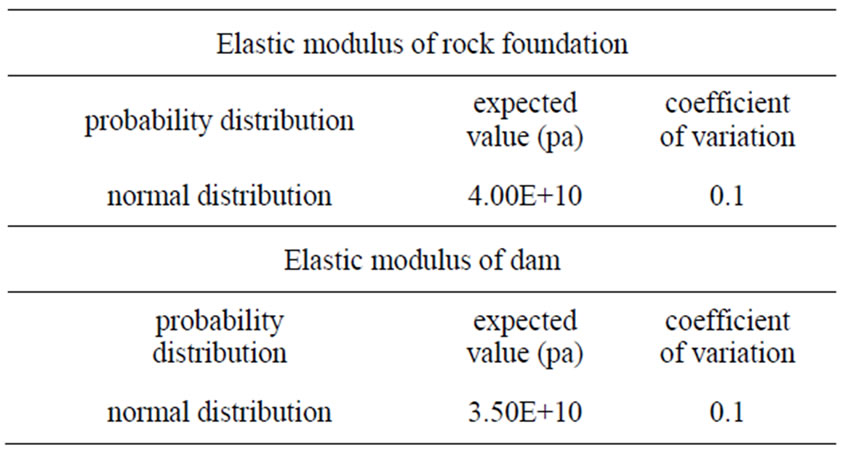
Table 3. The probability distribution of all random parameters of each element.
clusion that, under the condition of deterministic initial elastic modulus, the convergence rates of the expected values of tension damage factors of each element are fast. They generally turn to be stable at third iterative step. It shows the method of calculating expected values of tension damage factors has good convergence and stability. From Figure 4, Figure 5 and Table 4, we have the conclusion that, under the condition of random initial elastic modulus, the convergence rates are also fast. The deviation factor decreases exponentially which shows that the improved response surface method based on weighted regression also has good convergence and stability and greatly enhances calculation efficiency and the storage efficiency. And the method of analyzing large structure such as gravity dam is very applicable. The deviation factor reaches 0.16495 at the first iterative step. It shows that damage expected value is insensitive to the randomness of initial elastic modulus so we can neglect the randomness of initial elastic modulus in some extent when we calculate damage expected value. And we can obtain the guarantee rate about damage expected value is 75.755%.
5. Conclusions
In this paper, we analyze the probability of gravity dam damage. To begin with, based on pseudo excitation method and Mazar damage model, we calculate damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus is deterministic. Furthermore, we establish the improved response surface method based on weighted regression to analyze guarantee rate of damage expected value excited by random seismic loading and deterministic static load on the condition that initial elastic modulus is random. At last, we give a test example to verify and analyze the convergence and stability of this method. And it shows this algorithm has good convergence and stability and greatly enhances calculation efficiency and the storage efficiency. Through analysis of
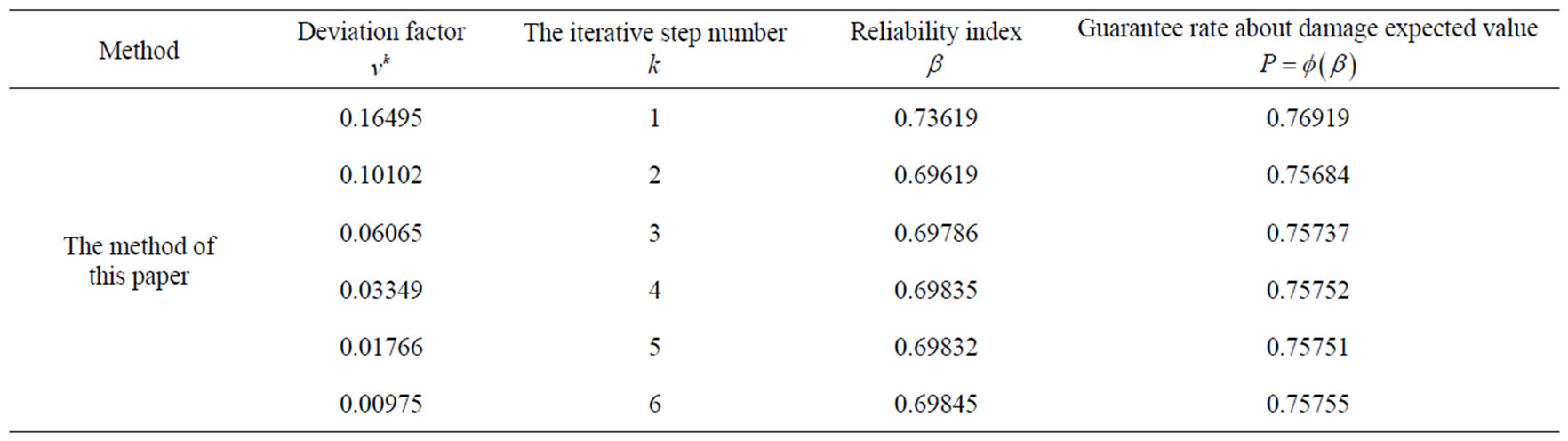
Table 4. The iterative procedure of improved response surface method based on weighted regression.
examples, we find that damage expected value is insensitive to the randomness of initial elastic modulus so we can neglect the randomness of initial elastic modulus in some extent when we calculate damage expected value.
6. REFERENCES
- Z. Kotulski and K. Sobczyk, “Effects of Parameter Uncertainty on the Response of Vibratory Systems to Random Excitation,” Sound Vibrator, vol. 119, No. 1, 1986, pp. 159-171.
- H. Benaroya and M. Rehak, “Finite Element Methods in Probabilistic Structural Analysis: A Selective Review,” Applied Mechanics Reviews, vol. 41, No. 5, 1987, pp. 201-213.
- P. D. Spanos and R. G. Ghanem, “Stochastic Finite Element Expansion for Random Media,” Journal of engineering mechanics, vol. 115, No. 5, 1989, pp. 1035-1053.
- P. Leger, R. Lariviere, F. Palavicini and R. Tinawi, “Performance of Gated Spillways during the 1996 Sanguinity Flood (Que’bec, Canada) and Evolution of Related Design Criteria,” Proceeding of ICOLD20th Congress, Beijing, vol. 26, No. 1, 2000, pp. 417-438.
- F.-Y. Wang, Z. S. Xu and L. J. Dong, “Stability Model of Tailing Dams Based on Fuzzy Random Reliability,” Chinese Journal of Geotechnical Engineering, Vol. 30, No. 11, 2008, pp. 1600-1605.
- R. Viertl, “On Reliability Estimation Based on Fuzzy Lifetime Data,” Journal of Statistical Planning and Inference, vol. 48, No. 5, 2008, pp. 1-6
- E. Castillo, R. Minguez and C. Castillo, “Sensitivity Analysis in Optimization and Reliability Problems,” Reliability Engineering and System Safety, vol. 93, No. 12, 2008, pp. 1788-1800. doi:10.1016/j.ress.2008.03.010
- J. H. Song and W. H. Kang, “System Reliability and Sensitivity under Statistical Dependence by Matrix-Based System Reliability Method,” Structural Safety, vol. 31, No. 2, 2009, pp. 148-156. doi:10.1016/j.strusafe.2008.06.012
- K. S. Chin, Y. M. Wang, G. K. K. Poon and J.-B. Yang, “Failure Mode and Effects Analysis Using a GroupBased Evidential Reasoning Approach,” Computers & Operations Research, vol. 36, No. 6, 2009, pp. 1768- 1799. doi:10.1016/j.cor.2008.05.002
- Y. W. Liu and F. Moses, “A Sequential Response Surface Method and Its Application in the Reliability Analysis of Aircraft Structural System,” Structural Safety, Vol. 16, No. 1-2, 1994, pp. 39-46. doi:10.1016/0167-4730(94)00023-J
- G. E. P. Box and K. B. Wilson, “The Exploration and Exploitation of Response Surfaces: Some General Considerations and Examples,” Biometrics, Vol. 10, No. 1, March 1954, pp. 16-60. doi:10.2307/3001663
- A. I. Khuri and J. A. Cornell, “Response Surfaces: Design and Analyses,” Marcel and Dekker, New York, 1997.
- R. H. Myers and D. C. Montgomery, “Response Surface Methodology: Process and Product Optimization Using Designed Experiments,” John Wiley and Sons, Hoboken, 1995.
- F. S. Wong, “Uncertainties in Dynamic Soil-Structure Interaction,” Journal of Engineering Mechanics, Vol. 110, No. 2, February 1984, pp. 308-24. doi:10.1061/(ASCE)0733-9399(1984)110:2(308)
- F. S. Wong, “Slope Reliability and Response Surface Method,” Journal of Geotechnical Engineering, Vol. 111, No. 1, January 1985, pp. 32-53. doi:10.1061/(ASCE)0733-9410(1985)111:1(32)
- L. Faravelli, “Response Surface Approach for Reliability Analysis,” Journal of Engineering Mechanics, Vol. 115, No. 12, 1989, pp. 2763-2781. doi:10.1061/(ASCE)0733-9399(1989)115:12(2763)
- L. Faravelli, “Structural Reliability via Response Surface,” In: N. Bellomo, F. Casciati, Eds., Proceedings of IUTAM Symposium on Nonlinear Stochastic Mechanics, Springer Verlag, Berlin, 1992, pp. 213-223.
- J. Q. Jiang, C. G. Wu, C. Y. Song, et al., “Adaptive and Iterative Gene Selection Based on Least Squares Support Vector Regression,” Journal of Information & Computational Science, Vol. 3, No. 3, 2006, pp. 443-451.
- C. G. Bucher and U. Bourgund, “A Fast and Efficient Response Surface Approach for Structural Reliability Problems,” Structural Safety, Vol. 7, No. 1, 1990, pp. 57- 66. doi:10.1016/0167-4730(90)90012-E
- M. R. Rajashekhar and B. R. Ellingwood, “A New Look at the Response Surface Approach for Reliability Analysis,” Structural Safety, Vol. 12, No. 3, 1993, pp. 205-220. doi:10.1016/0167-4730(93)90003-J
- X. L. Guan and R. E. Melchers, “Effect of Response Surface Parameter Variation on Structural Reliability Estimates,” Structural Safety, Vol. 23, No. 4, 2001, pp. 429- 444. doi:10.1016/S0167-4730(02)00013-9
- S. Gupta and C. S. Manohar, “Improved Response Surface Method for Time Variant Reliability Analysis of Nonlinear Random Structures under No Stationary Excitations,” Nonlinear Dynamics, Vol. 36, No. 2-4, 2004, pp. 267-280. doi:10.1023/B:NODY.0000045519.49715.93
- P. Bjerager, “Methods for Structural Reliability Computation,” In: F. Casciati, Ed., Reliability Problems: General Principles and Applications in Mechanics of Solid and Structures, Springer Verlag Wien, New York, 1991, pp. 89-136.
- B. Fiessler, H.-J. Neumann and R. Rackwitz, “Quadratic Limit States in Structural Reliability,” Journal of the Engineering Mechanics Division, Vol. 105, No. 4, 1979, pp. 661-676.
- K. Breitung, “Asymptotic Approximation for Multi-Normal Integrals,” Journal of Engineering Mechanics, Vol. 10, No. 3, 1984, pp. 357-366. doi:10.1061/(ASCE)0733-9399(1984)110:3(357)
- H. U. Koyluoglu and S. R. K. Nielsen, “New Approximations for SORM Integrals,” Structural Safety, Vol. 13, No. 4, 1994, pp. 235-246. doi:10.1016/0167-4730(94)90031-0
- A. D. Kiureghian, H. Z. Lin and S. J. Hwang, “Second-Order Reliability Approximations,” Journal of Engineering Mechanics, Vol. 113, No. 8, 1987, pp. 1208- 1225. doi:10.1061/(ASCE)0733-9399(1987)113:8(1208)
- J. Zhao and Z. Z. Lu, “Response Surface Method for Reliability Analysis of Implicit Limit State Equation Based on Weighted Regression,” Journal of Mechanical Strength, vol. 28, No. 4, 2006, pp. 512-516.
NOTES
Fund projects: National Basic Research Program of China (973 projects 2007CB714107); Trans-Century Training Programmer Foundation for the Talents by the State Education Commission (NCET- 06-0270)

