Engineering
Vol. 3 No. 1 (2011) , Article ID: 3717 , 4 pages DOI:10.4236/eng.2011.31002
Research on Irradiation Electric Field for Charged Particles Beam with High Energy
1College of Physics and Electronic Information, Anhui Normal University, Wuhu, China;
2State key Lab. of Optical Tech. for Microfabrication, Institute of Optics and Electronics,
Chinese Academy of Science, Chengdu, China
E-mail: shi_jian_ping@hotmail.com
Received October 9, 2010; revised November 29, 2010; accepted December 8, 2010
Keywords: Charged-Particles Beam with High Energy, Irradiating Damage, Irradiation Electronic Field, α Ray, β Ray
ABSTRACT
Irradiation protection of the nonlinear optical devices used in the spacecraft and next generation active laser system must be solved. The first problem was to find the irradiation damage mechanism of the nonlinear materials. In this paper the irradiation electronic field originating from high speed charged particle beams was discussed. The calculating model of the electronic field, based on the relativistic mechanics and electro-magnetic theory, was founded. The common characters of the irradiation electronic field were predicted and the fields of α ray and β ray were calculated by means of our model. The simulating results showed that the intensity of the electric field increased with the energy or the intensity of the beam. The results also showed that the field change trend of α ray and β ray was similar, but the field value was quite different. When the beam intensity I = 100 μA and the beam energy εm = 500 Mev, the electronic field values were about 3.5 × 107 v/m for α ray and 2.4 × 1011 v/m for β ray.
1. Introduction
With rapid progress of research on photoelectric countermeasures technology, all kinds of photoelectric reconnaissance warning system, photoelectric active/passive disturbance system, and photoelectric counter-reconnaissance and anti-disturbance system are of increasingly outstanding significance for military purpose. Application of non-linear materials is increasingly wide [1-3]. For example, the solid laser pump optical oscillator which is researched with very rapid progress adopts conversion technology under frequency of non-linear crystalloids, converting 1~2 μm near-infrared laser into 3~5 μm moderate-infrared laser, for realization of miniaturization, full solidification, wide spectrum, and high power of laser device. Also for example, the current commonly used gas Medium infrared laser can also have output of 4.6~5.4 μm laser through frequency multiplication of non-linear material using CO2 laser device, further having output of 3 μm wavelength through beat frequency, and so on [4]. On account of special application environment of these systems, non-linear materials may very possibly have defects due to irradiation resulting from all kinds of natural or artificial rays (e.g. α-ray, -ray, and γ-ray etc.) as well as heavy and light ions etc [5]. Therefore, the irradiating damage mechanism of nonlinear materials is a problems demanding urgent solution in the fields of military, aviation, and aerospace.
Material irradiation damage has been researched since 1950s and in-depth research has been made for metal, glass, plastic and semi-conductor materials etc, establishing many models (e.g. Coulomb explosion model, track core plasma model, thermal spike model) to explain change in shape as well as mechanical, optical, and electrical properties etc. A large mount of experiments has verified that these theoretical models are correct [6-10]. However, it is unsuitable to directly use these models to research irradiation damage of non-linear materials because these theoretical models are based on such thermal effects as atom displacement, formation of defects, and plastic deformation etc. resulting from irradiation particles bombarding target materials, which has ignored influence by kinematics electric field of live particles. Of course, it is suitable for metallic and semi-conductor parts because thermal effect is a main factor resulting in its damage. However, it is not true for non-linear materials placed into radiation space. Here radiation electric field has been key factor influencing its optical properties. Even if there is not thermal damage, non-linear coefficient may possibly be changed due to influence by irradiation electric field. Currently, many people have been enthusiastic about research on influence of electric field to material non-linear coefficient in leading-edge research. In 1995, G. J. Ashwell et al. released breakthrough achievement of non-linear optical theory on Nature, that is, he observed generation of second harmonic wave from symmetrical dye in center of the second order non-linear coefficient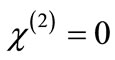 , of which second harmonic wave results from excited electrical quadrupole excitation effect caused externally applied electric field violently modulated by photon crystalloid structure [11]. Based on above-mentioned principle, Martorell and Teruya Ishihara designed and realized change of electric field to non-linear coefficient of polystyrene particulates and PMMA films in 1998 and 2003 respectively [12,13]. The Chinese Shi Jianping et al. has also ever researched the influence of externally applied electric field’s gradient to Si material non-linear properties. The researches show that magnitude, direction, and shape of electric field can greatly influence non-linear coefficient [14-16].
, of which second harmonic wave results from excited electrical quadrupole excitation effect caused externally applied electric field violently modulated by photon crystalloid structure [11]. Based on above-mentioned principle, Martorell and Teruya Ishihara designed and realized change of electric field to non-linear coefficient of polystyrene particulates and PMMA films in 1998 and 2003 respectively [12,13]. The Chinese Shi Jianping et al. has also ever researched the influence of externally applied electric field’s gradient to Si material non-linear properties. The researches show that magnitude, direction, and shape of electric field can greatly influence non-linear coefficient [14-16].
Therefore, for non-linear material placed into moving charged particles space at high speed, it is a new subject of material radiation protection to understand how irradiation electric field excited by moving charged particles space at high speed can influence non-linear material on earth. And, priority shall be given to calculate magnitude of irradiation electric filed and to analyze its shape with various irradiation parameters of different charged particles. However, few researches on irradiation electric field of charged particles can be found from existing literatures. This paper first establishes calculation model of charged particles irradiation electric field and then calculates irradiation electric fields of two kinds of charged particles (i.e., α- ray and β- ray) under various irradiation condition and analyzes characteristics of electric field by comparison.
2. Calculation Model
An electromagnetic field excited by moving live particles beam stream is a complicated and autonomous problem. Consideration must be made for relationship between static electrical force among the live particles and shape of beam stream, of which calculating process is very complicated but our concerns are magnitude of electric field under a certain beam stream condition. Therefore, the beam stream shape may be assumed to be unchanged within certain duration, that is, without consideration of beam stream cave effect resulting from interaction among live particles, so as to avoid complicated calculation of electromagnetic field. The main parameters describing particles radiation include energy of ray, strength of beam stream, and velocity of particle.
Given high-energy live particles beam presenting cylindrical shape, with radius being a, the particles beam moving alongside Axis z, the center coinciding with Axis z, moving velocity being v, the observing point locating at Point P(x,y,z) not on the Axis, the spatial coordinate relationship is shown as Figure 1. Given strength of particles beam stream being I, cross-section area of beam stream being s, any thin round charged piece perpendicular to Axis z, with a radius being r, the thickness of thin piece being dz, the total amount of charge applied on the thin piece is:
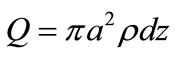 (1)
(1)
where: density of Particles Beam electric charge volume density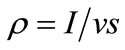 .
.
Given charge evenly distributed within thin piece, the movement of charge on thin piece may be equivalent to the movement of point charge having charge of Q. The electric field generated may be taken using the retarded potential formula [17],
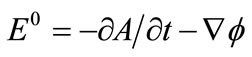 (2)
(2)
where, 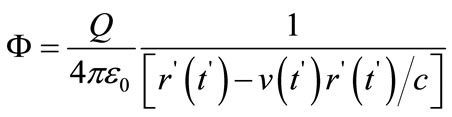 ,
,  is Lienard-Weichert potential,
is Lienard-Weichert potential, 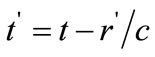 is the retarded time.
is the retarded time.
From Equation (2), taken as
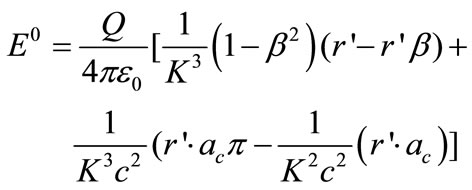 (3)
(3)
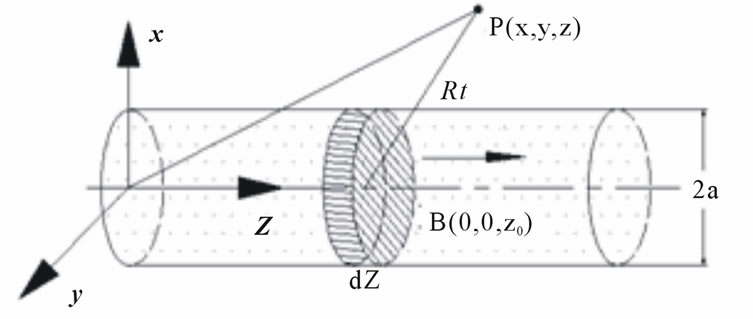
Figure 1. Coordinate diagram of charged particles beam with high energy.
Where, β=v/c,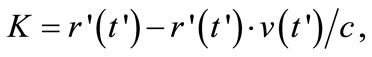 ac is acceleration and C is the light velocity.
ac is acceleration and C is the light velocity.
When live particles move at constant speed, ac = 0, here taken as
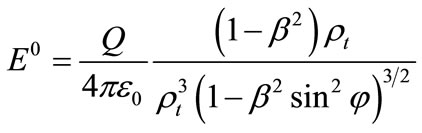 (4)
(4)
where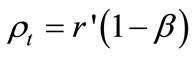 ,
, ![]() is point–to–point flare angle of charge. Break the electric field down to two quantities respectively parallel to Axis z and perpendicular to Axis z, taken as:
is point–to–point flare angle of charge. Break the electric field down to two quantities respectively parallel to Axis z and perpendicular to Axis z, taken as:
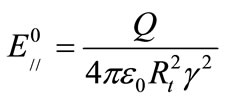 (5)
(5)
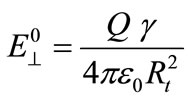 (6)
(6)
where, 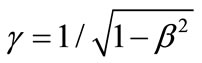 factor of relative theory,
factor of relative theory, 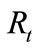 = the radius vector from thin piece charge center Z0 to observing point. The electric field generated by moving particles beam results from superimposition of single thin piece charge electric field. The horizontal component of electric field resulting from particles beam can be taken through integral to Equation (9) alongside Axis z.
= the radius vector from thin piece charge center Z0 to observing point. The electric field generated by moving particles beam results from superimposition of single thin piece charge electric field. The horizontal component of electric field resulting from particles beam can be taken through integral to Equation (9) alongside Axis z.
 (7)
(7)
Likewise, the vertical component of electric field resulting from particles beam can be taken;
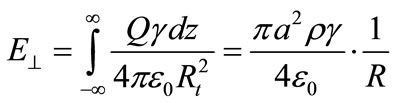 (8)
(8)
Therefore, magnitude of total field is:
 (9)
(9)
Replacing the factor of relative theory with kinetic energy, i.e.,
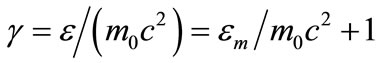 , taken as:
, taken as:
 (10)
(10)
These are irradiation electric field and irradiation parameters excited by charged particles beam: The calculating model among strength of beam stream (I), velocity of particles (v), energy of ray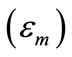 , where ε = vacuum dielectric constant being 8.85 × 10-12 F/m,c = vacuum light velocity being 3.0 × 108 m/s,m0 = static mass, R = the distance of particle from the observing point to central axis of particles beam.
, where ε = vacuum dielectric constant being 8.85 × 10-12 F/m,c = vacuum light velocity being 3.0 × 108 m/s,m0 = static mass, R = the distance of particle from the observing point to central axis of particles beam.
3. Calculation and Analysis on Irradiation Electric Field of β-ray and α-ray
In order to more directly analyze magnitude and changing trend of radiation electric field, use Equation (10) to respectively calculate magnitude of irradiation electric field of β-ray and α-ray under various radiation conditions. See Figure 2.
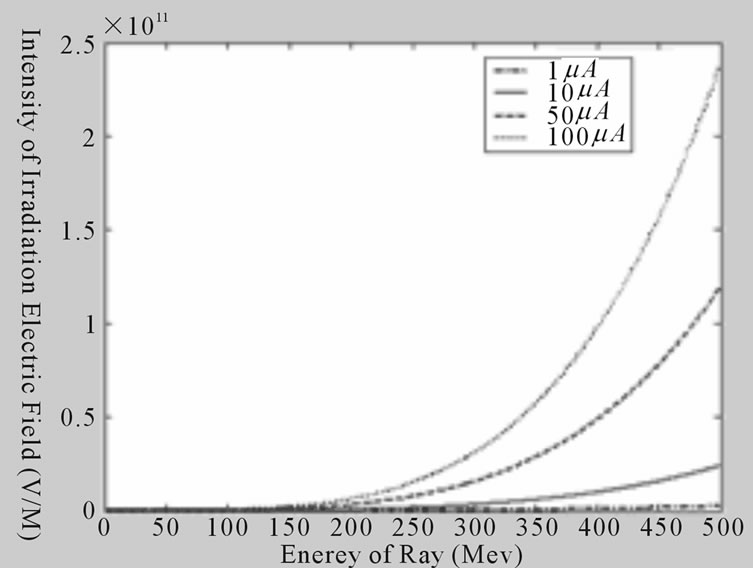
The intensity of irradiation electric field of β-ray is showed in Figure 2(a) when the energy of ray is continuously changed from 0.5 Mev to 500 Mev in case of beam intensity being 1 μA, 10 μA, 50 μA, and 100 μA. According to the figure and under certain strength of beam stream, the higher the energy of ray is, the bigger the irradiation electric field. When I = 100 μA, εm = 500 Mev, the value of field strength has been up to 2.4 × 1011 v/m, higher than typical field strength (approximately being 108 magnitude level) of commonly used laser by more than one thousand times. If non-linear material is placed into such irradiation environment, the second order non-linear coefficient is inevitably changed, which is what we will focus on in the near future. Figure 2(a) also shows the changing trends of electric field with various strengths of beam stream is different. If the strength (I) of beam stream is smaller, the field strength more slowly varies with strength of beam stream. As (I) is increasing, the strength of beam stream quickens significantly. Additionally, according to the figure, when energy of ray is fixed, the field strength increases with increasing strength of beam stream, which represents that electric charge volume density of beam stream is an important factor influencing electric field.
Figure 2(b) shows calculation of α-ray. For purpose easy comparison, the changing curve of irradiation y electric field is calculated when energy of ray continuous varies from 0.5 Mev to 500 Mev in case of beam intensity being 1μA, 10 μA, 50 μA, 100 μA. By comparison Figures 2(a-b), the changing trends of both are fully consistent. However, the magnitude of field strength under same condition is apparently different. When I = 100 μA and εm = 500 Mev, the electric field value of α-ray is 3.5 × 107 v/m approximately, significantly reduced comparing with that of β-ray under same condition. Because mass of α particle is heavier than that of β particle by ten thousand times approximately, the velocity of α particle is far less than that of β particle, which causes that the excited electric field is unlike with β-rays which concentrate on the direction perpendicular to the axis instead of presenting on both of horizontal and vertical directions. Therefore, the total field strength will signifi-
 (a)β Ray
(a)β Ray (b)αRay
(b)αRay
Figure 2. Irradiation electric field of two common ray.
cantly be reduced after superimposition of field strengths. Thus it can be seen, under same irradiation condition, the electric field excited by α-ray is smaller, equivalent to general laser illuminant, as a maximal. It will hardly result in damage to non-linear materials. Therefore, consideration is mainly be made for situation of β ray when analyzing influence of electric field to non-linear materials.
4. Conclusion
The irradiation damaged of material by high energy particles mainly presents deformation of material resulting from direct bombarding. Here thermal effect is a main factor damaging materials. Influence of irradiation electric field may fully be ignored. Therefore, few researches on influence of material properties by irradiation electric field can be found from existing literatures. However, for non-linear material placed into irradiation space, irradiation electric field has been a major factor which is unable to be ignored and it is especially true when particles are not directly bombarding the materials. According to the results of this paper, electric field resulting from irradiation particles is very strong when they have very high energy. Especially, β particles electric field with light mass and high velocity can sufficiently result in damage to non-linear material. The influence of non-linear material by such irradiation electric field will be researched soon.
5. Acknowledgment
This work was supported by Natural Science Foundation of China (No. 10805001), Key Project of Chinese Ministry of Education (NO. 210099) and Science Research Project of Anhui Province Education Department (No. 2006kj262B).
6. REFERENCES
- M. Matishak, “ABL Completes Payload Tests will Prepare for Laser Integration,” Inside Missile Defense, Vol. 11, No. 17, 2005, pp. 136-145.
- R. Preston, D. J. Johnson et al., “Space Weapons: Earth Wars,” RAND, Santa Monica, 2003.
- H. S. Ji, Z. Y. Qin and D. X. Zhao, “Experience and Prospects of Foreign Laser Weapons,” Laser & Optoelectronics Progress, Vol. 43, No. 5, 2006, pp. 8-15.
- M. Zhong and G. Ren, “3~5μm Medium Infrared Laser Countermeasure Weapon System,” Sichuan Ordnance Journal, No. 1, 2007, pp. 8-15.
- R. F. Hodson1, K. Somervill1, J. Williams2, et al., “Architecture for Reconfigurable Computing in Space,” NASA Office of Logic Design, Washington DC, September 2005.
- Z. G. Wang, Y. F. Jin and M. D. Hou, “Experimental Study of Electronic Energy Loss Effects in Pure Metals,” Nuclear Physics Review, Vol. 17, No. 2, 2000, pp. 26-31.
- S. Y. Zhu, A. L. Li and Q. Luo, “Positron Annihilation Study of Defects in GaP Radiated by Fission Neutron,” Journal of Nuclear Science and Technology, Vol.34, No. 8, 1997, pp. 23-29.
- D. R. Schmitt, G. Ringel, F. Kratz, R. Neubauer, H. Swoboda and J. Hampe, “Degradation Effects of Optical Components in the Low Orbit,” 17th International Symposium on Materials in Space Environment, Toulouse, 1997, pp. 257-263
- F. Hegeler, M. O. Manasreh, C. Morath, et al., “Thermal Annealing Recovery of Intersubband Transitions in Proton Irradiated GaAs/AlGaAs Multiple Quantum Wells,” Applied Physics Letters, Vol. 77, No. 18, 2000. doi:10.10 63/1.1320846
- G. M. Swift, S. Rezgui, J. George, C. Carmichael, et al., “Dynamic Testing of Xilinx Virtex-II Field Programmable Gate Array (FPGA) Input/Output Blocks (IOBs),” IEEE Transactions On Nuclear Science, Vol. 51, No. 6, 2004, pp. 3469-3474. doi:10.1109/TNS.2004.839190
- G. J. Ashwell, G. Jefferles, D. G. Hamilon et al, “Strong Second-Harmonic Generation from Centrosymmetric Dyes,” Nature, Vol. 375, June 1995, pp. 385-388. doi:10. 1038/375385a0
- J. Martorell, R. Vilaseca and R. Corbalan, “Second Harmonic Generation in a Photonic Crystal,” Applied Physics Letters, Vol. 70, No. 6, 1997, pp. 702-704. doi:10.1063/1. 118244
- T. Ishihara and K. Koshino, “Second Harmonic Generation Due to Quadrupole Interaction in a Photonic Crystal Slab: Angle Dependence and Symmetry of the Unite Cell,” Applied Physics Letters, Vol. 91, No. 25, 2003. doi:10. 1103/PhysRevLett.91.253901
- J. P. Shi, X. Luo, X. Chen and C. Du, “Analysis of Optical SHG in Photonic Crystals Consisting of Cetro-Symmetric Dielectric,” Optics Express, Vol. 12, No. 22, 2004. doi:10.1364/OPEX.12.005307
- X. Luo, J. P. Shi, H. Wang and G. Yu, “Surface Plasmon Polaron Radiation from Metallic Photonic Crystal Slab,” Modern Physics Letters B, Vol. 18, 2004. doi:10.1142/ S0217984904007475
- J. P. Shi, X. Chen, H. Li and H. Yao, “Second Harmonic Generation in Two Dimension Pcs Consisting of CentroSymmetric Dielectric,” International Journal of Modern Physics Letters B, Vol. 19, No. 5, 2005, pp. 869-873.
- Y. X. Luo, “Self Field of Charged Particles,” Press of Scientific and Technical Documentation, Beijing, October 1994 (in Chinese).

