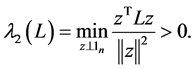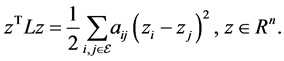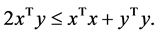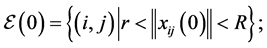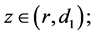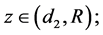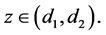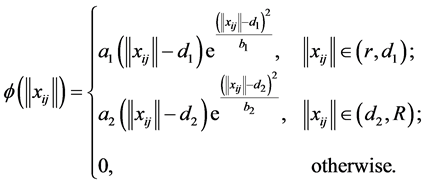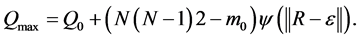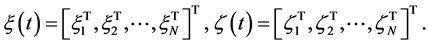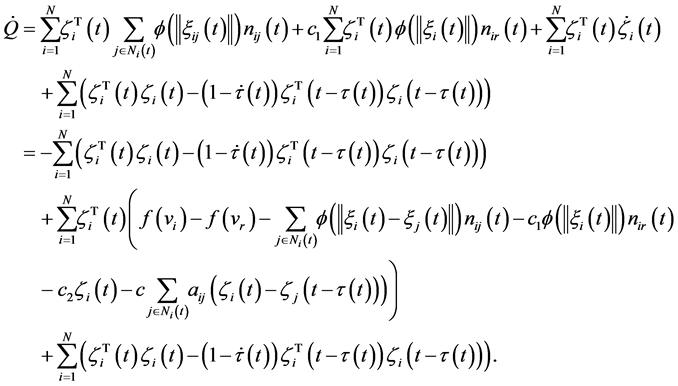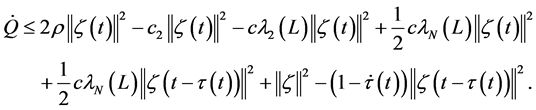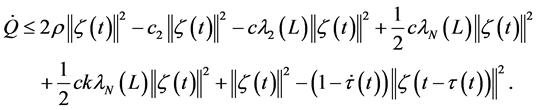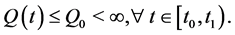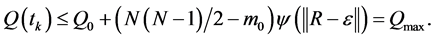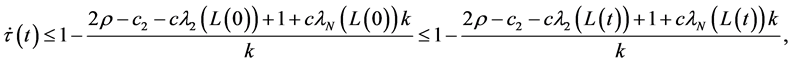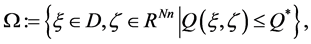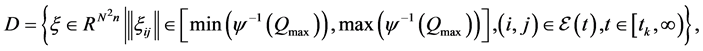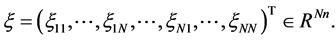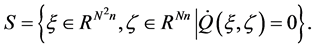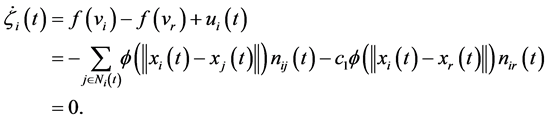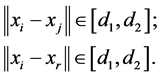Received 28 November 2015; accepted 3 February 2016; published 6 February 2016

ABSTRACT

This paper investigates the flocking problem in multi-agent system with time-varying delay and a virtual leader. Each agent here is subject to nonlinear dynamics. For the system, the corresponding algorithm with time-varying delay is proposed. Under the assumption that the initial network is connected, it is proved that the distance between agents is in the desired distance. The theore- tical deduction shows that the stable flocking motion is achieved.

Keywords:

Flocking, Time-Varying Delay, Nonlinear Dynamics, Multi-Agent System, Virtual Leader

1. Introduction

Flocking is a collective behavior of large number of interacting agents with a common group objective. Examples of these agents include birds, fish, penguins, ants, bees, and crowds. Many scientists from rather diverse disciplines, including physics, mathematics, control engineering and biology, have been interested in flocking problem [1] -[8] . The first well-known flocking model was proposed by Craig Reynolds [2] . Reynolds started with a boid model to build a simulated flock and introduced three rules (i.e., separation, cohesion and alignment rules) for flocking. Based on Reynolds’ three rules, flocking problems have been investigated from various perspectives [9] -[15] . In [16] , an artificial potential function is put forward and three algorithms are introduced. It provides a theoretical framework for the designing of flocking algorithms. Multi-agent flocking under topological interactions is considered, which define a notion of hierarchical structure in the interaction graph that establish conditions building upon previous work on multi-agent systems with switching communication networks in [17] . Using structurally balanced signed graph theory and a specified potential function, a stable bipartite flock formation is achieved for both virtual leader and leaderless situations in [18] . However, there is a common assumption that virtual leaders guide the flocking behaviors of the group. In this paper, leader follower flocking problem of multi-agent system is considered.

A flocking problem concerning multiple leaders in which followers use the position of flocking center to keep their connections is studied in [19] . In [20] , two leader-follower adaptive flocking algorithms are proposed with the combination of consensus and attraction/repulsion function respectively to solve the cohesive flocking problem and the formation flocking problem. Aiming at the group of autonomous agents consisting of multiple leader agents and multiple follower ones, a flocking behavior method with multiple leaders and a global trajectory was proposed in [21] . Yu et al., [22] give a distributed leader-follower algorithm considering the group consisting of one leader. In [23] , for the circumstance with a virtual leader, the agents would follow the virtual leader and achieve the same velocity asymptotically.

In practice, time delay is inevitable and would damage the stability of system. Jing et al. [23] investigate flocking problem of multi-agent systems with time delay and discuss systems with homogeneous and inhomogeneous time delay. Yang et al. [24] proposed an adaptive flocking algorithm for multi-agent system with time delay. It is proved that the distance between agents can be larger than a constant during the motion evolution by using the flocking algorithm. The authors investigate the flocking problem of multi-agent systems led by one active virtual leader with a directed topology containing time-varying coupling delays, which based only on the three classical assumptions for flocking systems in [25] . Because of these problems, this paper will study the flocking problems in the multi-agent system with a virtual leader and time-varying delay.

The rest of this paper is organized as follows. Some basic preliminaries and flocking algorithms are presented in Section 2. Section 3 gives the nonlinear leader-following multi-agent models. Algorithms and main results are presented in Section 4. Section 5 concludes the paper and offers suggestions for future work.

2. Preliminaries

In this section, some related preliminary knowledge are introduced. For any vector 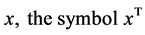denotes its transpose and 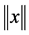denotes the Euclidean norm. Let 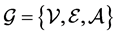be a weighted undirected graph with the set of nodes 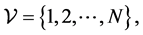and the set of agents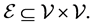

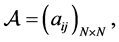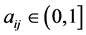Graphs with self-loops will not be considered in this paper. The weight adjacency matrix where if 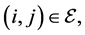otherwise, 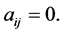An edge denoted by the pair 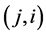represents a commu- nication link from node j to i. A path 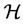from node i to node j is a sequence of edges, 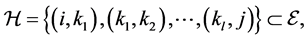in which all nodes 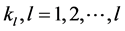are distinct. An undirected graph is called connected if there is a path between each pair of distinct nodes. 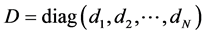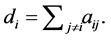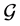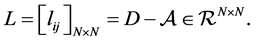is the degree matrix whose diagonal elements are defined by The Laplacian matrix of graph is Then it has following properties [26] ,

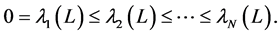
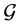
1) The eigenvalues of L satisfy If the graph is connected, there is

2) The Laplacian matrix L is a positive semi-definite matrix that satisfies the following sum-of-squares property:

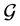
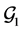
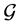
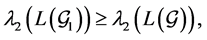
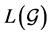
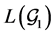
Lemma 1. [4] Suppose that is an undirected graph of order N, and is a graph generated by adding some edges into the graph. Then where and are the symmetric Laplacian matrices of graphs and, respectively.

Lemma 2. For any vectors 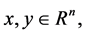the following matrix inequality holds:

3. Problems Formulation

Consider the multi-agent system described by

(1)

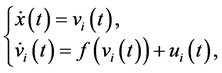
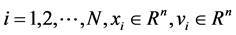
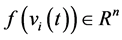
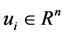
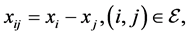
where are the position and velocity states of i^th agent, respectively. is the nonlinear dynamic of agent i and is the control input. Denote as the relative distance between agent i and agent j.

For the systems with virtual leader available, the dynamics of virtual leader is described as

(2)

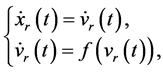
where 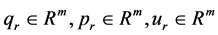represent the position, velocity and control input vector of the virtual leader.

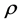
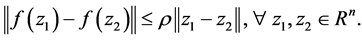
Assumption (A): There exists a positive constant satisfying

(3)

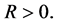
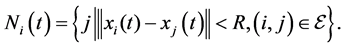
Supposed that all agents have the same sensing radius Then the neighboring set of agent i is denoted as Since the size of agent cannot be ignored usually that a minimum allowable distance r (collision distance) is considered in the model.

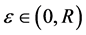
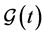
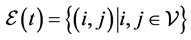
Definition 1: Given a constant, is called a dynamic undirected graph with a time-varying set of links such that

1) Initial links are generated by

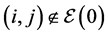
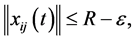
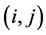
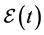
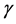
2) If and then is a new link to be added. It is called hysteresis effect and is the hysteresis distance, which is crucial in preserving connectivity of the network;

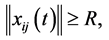
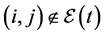
3) If then.

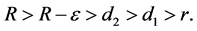
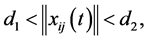
The neighboring set of agent i is divided into four regions, named collision region, separation region, alignment region and attraction region, in which If agents i and j are in desired distance.

Definition 2. is a bounded function with respect to between agents i and j, which satisfies

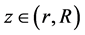
1) when

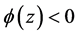
2) when

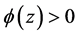
3) otherwise.

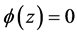
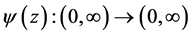
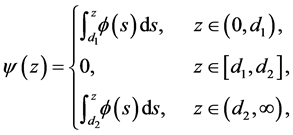
Definition 3. The pairwise bounded potential function can be defined.

(4)

which satisfies

1) decreases with the increase of z when.

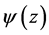
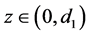
2) is increasing on. Obviously, the potential function reaches its minimum value 0 when

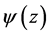
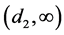
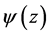
According to conditions, 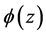can be constructed as follows:

where the parameters 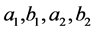are positive constants. There are, and

4. Algorithms and Main Results

For system (1) with virtual leader (2), the flocking algorithm can be described by

(5)

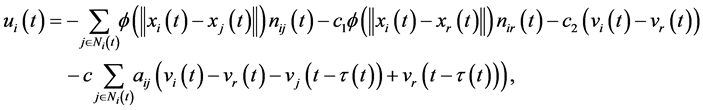
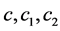
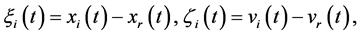
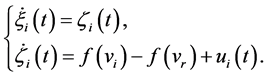
where are positive constants. Denote respectively. Then the system can be described by

(6)

The control input (6) can be equivalently rewritten as

(7)

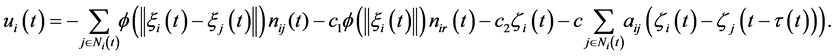
Denote

Definition 4. Flocking motion with a virtual leader is said to be achieved asymptotically for systems (1) and (2), if for any initial state, there is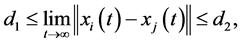

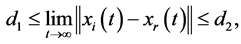
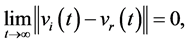
To demonstrate the validity of control protocol (7), the following positive semi-definite function is constructed

(8)

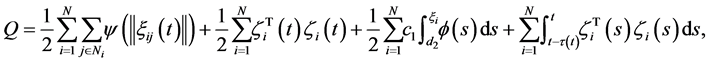
where.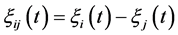

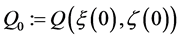
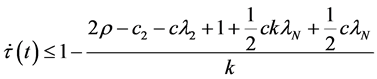
Theorem 1. Consider a multi-agent system modeled by dynamics (1) and (2), driven by control protocol (5). Suppose that the network is initially connected and is bounded.When

, then following statements hold,

1) is connected for all;

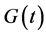
2) No collision occurs among agents for all;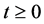

3) Flocking motion with a virtual leader is achieved asymptotically.

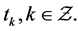
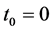
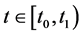
Proof: Denote the topology switching time sequence as Without loss of generality, assume. Taking the time derivative of the Lyapunov function Q on gives

From Lemma 2, there is

For a positive constant k, one has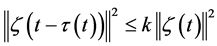, thus

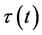
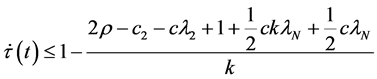
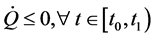
Assume that satisfy, there is

,

which implies that

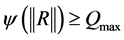
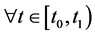
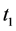
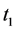
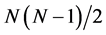
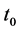
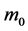
By definition (2), one has. Therefore, no edge distance will be tend to R for, implying that no existing edges will be lost before time. Hence, new edges must be added into the network at. For a system consists of N agents, there are at most edges. At the initial instant, the system consists of edges, then

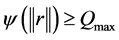
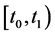
Hence there is no edge lost. In addition, from the definite of potential function, one has. Therefore, no collision occurs during.

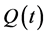
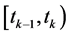
Similar to the above analysis, taking the time derivative of on every. By lemma 1, there is

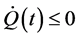
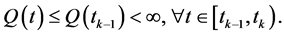
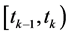
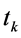
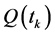
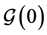
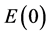
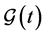
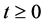
one has, which implies Thus no edge distance will tend to R for, implying that no edge will be lost before time and is finite. Since is connected and no edge in is lost, will be connected for all. This completes the proof of part (1).

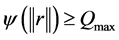
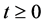
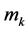
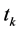
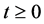
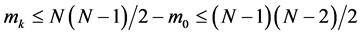
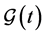
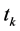
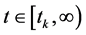
Similarly, from, deducing that no edge distance will tend to r, for all. Thus collision is avoided during the whole process. This completes the proof of part (2). To proof part (3), assume that there are new edges being added to the evolving network at time. As no edges are lost for, and. Therefore, the number of switching times of the system (1) is finite, which implies that the evolving network eventually becomes fixed. Denote the last topology switching as. Then Q is continuous and monotonously decreasing for. Hence the set

is positively invariant, where

and

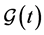
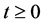
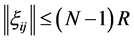
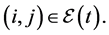
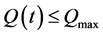
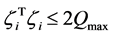
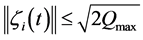
Since is connected for all, one has, for all As, one

has. thus. Therefore, the set Ω is compact. It follows from LaSalle’s invariance

principle that if the initial condition lies in Ω, then the corresponding trajectories will converge to the largest invariant set inside the region

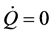
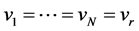
From (8), if and only if, which implies that the velocities of all agents will converge to that of the virtual leader asymptotically.

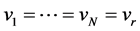
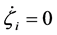
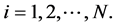
Since, there is for all From (6), one has

Thus, unless the inital configuration of the agents is close enough to the global minimum, almost every final configuration locally minimizes each agent’s global potential. which implies

Then the flocking is achieved. This completes the proof of part (3), thus Theorem 1 hold.

Remark 1. If 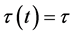is the constant delay, from the deduction above, Theorem 1 is also hold.

5. Conclusion

This paper mainly discusses the flocking problem of multi-agent system with a virtual leader and time-varying delay. Unlike most existing flocking algorithms, each agent here is subject to nonlinear dynamics. The corresponding algorithms with the time-varying delay are proposed. Under the assumption that the initial network is connected, the theoretical deduction is made. The related topic over the directed network or the jointly connected network will be studied in future.

Acknowledgements

We thank the Editor and the referee for their comments. This work was supported by the National Nature Sci- ence Foundation of China under Grants 61503053, 61472374 and 61304197, the Natural Science Foundation Pro- ject of CQ CSTC, China (Grant No. cstc2013jcyjA40018), the Youth Science Research Project of CQUPT, China (Grant Nos. A2012-78 and A2012-82), the Doctor Start-up Foundation of CQUPT, China (Grant Nos. A2012-23 and A2012-26), the Natural Science Fundation of CQJW, China (Grant Nos. KJ130506 and KJ1400435), and Training Programme Foundation for the Talents of Higher Education Commission. This support is greatly appreciated.

Cite this paper

FenglanSun,RuiWang,YongfuLi,FengLiu, (2016) Flocking for Leader-Following Multi-Agent Systems with Time-Varying Delay. Intelligent Control and Automation,07,9-15. doi: 10.4236/ica.2016.71002

References