Intelligent Control and Automation
Vol.06 No.04(2015), Article ID:60889,14 pages
10.4236/ica.2015.64021
Adaptive Control for a Class of Systems with Output Deadzone Nonlinearity
Nizar J. Ahmad1, Ebraheem K. Sultan1, Mohammed Q. Qasem1, Hameed K. Ebraheem1, Jasem M. Alostad2
1Faculty of Electronic Engineering Technology, College of Technological Studies, The Public Authority for Applied Education and Training (PAAET), Kuwait City, Kuwait
2Faculty of Computer Science, College of Basic Education, The Public Authority for Applied Education and Training (PAAET), Kuwait City, Kuwait

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 6 September 2015; accepted 1 November 2015; published 4 November 2015

ABSTRACT
This paper presents a continuous-time adaptive control scheme for systems with uncertain non- symmetrical deadzone nonlinearity located at the output of a plant. An adaptive inverse function is developed and used in conjunction with a robust adaptive controller to reduce the effect of deadzone nonlinearity. The deadzone inverse function is also implemented in continuous time, and an adaptive update law is designed to estimate the deadzone parameters. The adaptive output deadzone inverse controller is smoothly differentiable and is combined with a robust adaptive nonlinear controller to ensure robustness and boundedness of all the states of the system as well as the output signal. The mismatch between the ideal deadzone inverse function and our proposed implantation is treated as a disturbance that can be upper bounded by a polynomial in the system states. The overall stability of the closed-loop system is proven by using Lyapunov method, and simulations confirm the efficacy of the control methodology.
Keywords:
Adaptive Inverse Control, Output Deadzone, Hard Nonlinearity

1. Introduction
The problem of deadzone nonlinearity has been addressed by many researches with great success by utilizing adaptive control methods to eliminate the undesirable effects on the output of a plant [1] -[5] . Demonstrated in Figure 1 is the effect of deadzone on the output of a plant for a pure sinusoidal input trajectory. The majority of earlier investigations to this problem focus on the problem where the nonlinearity is located at the input of the plant as an actuator problem [1] [2] . In an actuator deadzone, the control effort is within the span of the nonlinearity which makes it somewhat easier to reduce or eliminate its deleterious effects before it enters the dynamics of the system to be controlled. As a matter of fact, several papers present a two structure control schemes that can be designed to handle deadzone as well as other requirements for plant performance criteria [3] . On the other hand, output deadzone, which is physically inherent in some sensors that measure output signals of a plant, is a more complicated problem. The control effort has to eliminate the deleterious effect of the deadzone nonlinearity whilst going through the complicated dynamics of the plant. Therefore, whatever added control requirements enforced on the designer due to disturbances or noise affecting the plant, will further complicated the task. One of the earliest investigations of output nonlinearities such as deadzone was presented by [4] . Their proposed methodology was based on output matching control which involved the design of an adaptive deadzone inverse used to reshape the input reference trajectory to negate the effect of the deadzone. The parameters of the deadzone were adaptively estimated by designing an error function utilizing the output to observe plants states. The implementation was quiet complex in design and implemented in discrete time. In [5] , an output feedback design was analysed for robustness and was developed using input to state stability (ISS) small gain tools. The combination of observer and controller design was proved to be essential when handling output nonlinearities. An adaptive compensation scheme without constructing a dead-zone inverse was presented in [6] . The proposed adaptive method requires only the information of bounds of the deadzone slopes and treats the time-varying input coefficient as a system uncertainty. The new control scheme ensures bounded-error trajectory tracking and assures the boundedness of all the signals in the adaptive closed loop. Tian Ping et al. utilized the integral-type Lyapunov function to design an adaptive compensation term for the upper bound of the residual and optimal approximation error as well as the dead-zone disturbance [7] . It was demonstrated that the closed- loop control system was semi-globally uniformly bounded. In [8] , an inverse deadzone function was incorporated in control system driven from a mathematical model of a deadzone in pneumatic servo valves. Tests were performed out using controllers with and without dead zone compensation to comparison validated the efficacy of the method. In [9] , a somewhat earlier work was presented in discrete time which successfully achieved reduction
Figure 1. The distortion effect of output deadzone nonlinearity on a sinusoidal of signal.
of the tracking error in plants with output deadzone nonlinearity while ensuring the global boundedness stability. The paper presented by Jing Zhoua et al. introduced a smooth approximation to the deadzone model which allowed them to employ back stepping technique [10] . In their approach, no knowledge was assumed of the uncertainty’s and the deadzone’s parameters. It is shown that the proposed controller not only can guarantee global stability, but also can achieve excellent transient performance. It is worthwhile to note that other non-classical control methods, such as fuzzy logic or neural network, have been presented by several researchers to reduce the effect of a deadzone nonlinearity [11] -[14] . For example, Wallace and Max used an adaptive fuzzy controller for nonlinear systems subject to dead-zone input. The boundedness of all closed-loop signals and the convergence properties of the tracking error are proven using Lyapunov stability theory and Barbalat’s lemma [15] .
Motivated by the success in producing successful results in handling input deadzone, we present an extended method to reduce the errors caused by output deadzone nonlinearity. The proposed method relies on the premise that by pre-shaping the input trajectory to mimic an inverse form of the deadzone nonlinearity, the combined effect will reduce if not completely eliminating the effect of output deadzone.
In this paper, a new continuous time robust adaptive output deadzone inverse controller (RAODI) is used in conjunction with a conventional model reference adaptive control to counter the distortions cause by output deadzone. The ideal deadzone inverse controller is approximated by an infinitely differentiable implementation to insure asymptotic tracking and minimized error generation. The overall stability of the system under the proposed scheme will be proven analytically and demonstrated by simulation to a practical application. The structure of the paper starts with a brief presentation of the dynamics of an output deadzone nonlinearity that defines various parameters and its effect on the output of a system are presented in Section 2. Meanwhile, the proposed control methodology is presented and its analytical proof using the Lyapunov argument is shown in Section 3. Consequently, an illustrative example of a model reference adaptive control scheme combined with the inverse control method is presented and followed by simulation results in Section 4.
2. The dynamics of Output Deadzone Nonlinearity
A common representation of a non-symmetrical deadzone nonlinearity, shown in Figure 1, can be described as follows
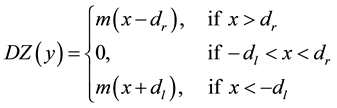 (1)
(1)
where
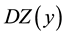 denotes the output of deadzone function,
denotes the output of deadzone function,
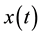 the output of a plant, m is the slope of the lines,
the output of a plant, m is the slope of the lines,
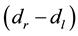 is the width of the deadzone distance, and
is the width of the deadzone distance, and
 is the input of the plant block as shown in Figure 2. Although the width of the deadzone spacing is assumed not to be exactly known, an upper bounds on it is given by
is the input of the plant block as shown in Figure 2. Although the width of the deadzone spacing is assumed not to be exactly known, an upper bounds on it is given by
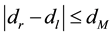 (2)
(2)
where
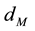 is a positive scalar. Output deadzone may also be written as
is a positive scalar. Output deadzone may also be written as
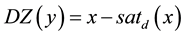 (3)
(3)
where
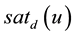 represents a non-symmetrical saturation function given by
represents a non-symmetrical saturation function given by
Figure 2. Non-symmetric deadzone nonlinearity as a function of a plant output signal.
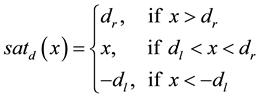 (4)
(4)
By defining a logical switching operator
 (5)
(5)
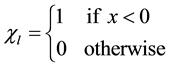 (6)
(6)
Then, the dynamics of the non-symmetrical deadzone presented in (3) can be rewritten as follows
 (7)
(7)
where



To obtain a smoothly differentiable implementation of (8), we replace it with a

with

Hence, rewriting Equation (5) and Equation (6) as


To proceed with the design of the compensator the following assumptions are required:
(A1) The deadzone parameters


(A2) The deadzone parameters




(A3) Without any loss of generality the slope of the deadzone

Assumption (A1) and (A2) are the actual physical attributes of a real industrial deadzone and is adopted in [16] . Therefore, the saturation function given by (4) is physically bounded

3. Robust Adaptive Controller Design
Considering the following nonlinear systems with input deadzone nonlinearity described as

where the matrices A and B are given by

Meanwhile, the unmeasurable disturbances represented as




The desired reference model is given by

where


where


Consequently, we can utilize (15) to construct the inverse deadzone model reference as

Hence, the states tracking error dynamics


where r is the desired reference signal. Equation (18) is written compactly as

where dynamics of

By defining the output tracking error



Once again, by ensuring that the plant states



where




or simply written as

where


Therefore, the deadzone effect noted by the term




where



The properties of the controller (25) are stated in the following theorem:
Theorem. For the plant described by (13) with input deadzone (1), and the RAODI control law (25) along with the adaptive update laws (22) and (26) will ensure the closed-loop stability and boundedness of tracking error, hence reducing the effects of deadzone on the control law driving the system dynamics and ensuresbounded output tracking.
Proof. Using the following positive definite control Lyapunov function

Differentiating along the trajectories of the system and substituting for the closed loop dynamics given by (19) yields

Applying the robust controller given in (25) into (28) gives

Collecting terms and simplifying


The first term can be simplified by solving the Algebraic Reccati Equation given by

which gives

Replacing the adaptation law (23) and replacing



Substituting the adaptive update law (7)


Utilizing Equation (23) for output tracking error

Renders the last term negative. For the third term, we utilize the general inequality


Applying this bound to (37)

By choosing the degree of freedom





4. Illustrative Example & Simulations
To illustrate the efficacy of the proposed compensator a second order sinusoidal desired reference model is selected for tracking. Simulations of the system in (22) under the adaptive control law (23) and (24) have been performed for a sinusoidal reference trajectory given by


where


friction and the electromotive force constant; and

vector



where the matrices A and B along with the gain k are given by

Meanwhile, the desired reference model to be tracked at the output for the overall system may be rewritten as

where




The proposed controller is given by

where the first term is the conventional PD-controller, the second term is the robust adaptive controller, and the third term is the adaptive deadzone inverse one.

Meanwhile, the initial value of


Figure 3 shows the output trajectory

The improvement in reducing the effect of output deadzone on the output signal is demonstrated in Figure 4 where the error

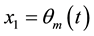



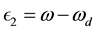



Table 1. Parameters utilized in the example.
Figure 3. The output trajectory

Figure 4. The output tracking error

Figure 5. The system state


Figure 6. The state tracking error

Figure 7. The system state


Figure 8. The second state error

Figure 9. The evolution of the robust adaptation
Figure 10. The evolution of the adaptation


Figure 11. Evolution of the control.
5. Conclusion
In this paper, an adaptive inverse deadzone controller is compared with a robust adaptive controller for systems with output deadzone nonlinearity. Both controllers have been shown to effectively stabilize a second order system, and achieve bounded input bounded output (BIBO) tracking. The proposed deadzone inverse controller has greatly improved the performance of the system over the robust controller. The deadzone inverse controller was implemented in continuous time and was used to modify a desired model reference to mimic an inverse deadzone trajectory. The RAODI is smoothly differentiable and can easily be combined with any of the advanced control methodologies. The stability of the closed-loop system has been proven by using Lyapunov arguments and simulations results confirm the efficacy of the control methodology.
Acknowledgements
This work is supported by the Public Authority for Applied Education and Training (PAAET) Kuwait grant number TS-14-03.
Cite this paper
Nizar J.Ahmad,Ebraheem K.Sultan,Mohammed Q.Qasem,Hameed K.Ebraheem,Jasem M.Alostad, (2015) Adaptive Control for a Class of Systems with Output Deadzone Nonlinearity. Intelligent Control and Automation,06,215-228. doi: 10.4236/ica.2015.64021
References
- 1. Ahmad, N.J., Alnaser, M.J. and Alsharhan, W.E. (2013) Asymptotic Tracking of Systems with Non-Symmetrical Input Deadzone Nonlinearity. International Journal of Automation and Power Engineering, 2, 287-292.
- 2. Tao, G. and Kokotovic, P. (1995) Discrete-Time Adaptive Control of Systems with Unknown Dead-Zones. International Journal of Control, 61, 1-17. http://dx.doi.org/10.1080/00207179508921889
- 3. Ahmad, N.J., Ebraheem, H.K., Alnaser, M.J. and Alostath, J.M. (2011) Adaptive Control of a DC Motor with Uncertain Deadzone Nonlinearity at the Input. 2011 Chinese Control and Decision Conference (CCDC), Mianyang, 23-25 May 2011, 4295-4299. http://dx.doi.org/10.1109/CCDC.2011.5968982
- 4. Toa, G. and Kokotovic, P. (1996) Adaptive Control of Systems with Actuator and Sensor Nonlinearities. John Wiley & Sons, Inc., New York.
- 5. Arcak, M. and Kokotovic, P.V. (2000) Robust Output Feedback Design Using a New Class of Nonlinear Observer. Proceedings of the 39th Conference on Decision and Control, Sydney, December 2000, 778-783.
- 6. Ibrir, S., Xie, W.F. and Su, C.-Y. (2007) Adaptive Tracking of Nonlinear Systems with Non-Symmetric Dead-Zone Input. Automatica, 43, 522-530. http://dx.doi.org/10.1016/j.automatica.2006.09.022
- 7. Zhang, T.-P., Zhou, C.-Y. and Zhu, Q. (2009) Adaptive Variable Structure Control of MIMO Nonlinear Systems with Time-Varying Delays and Unknown. International Journal of Automation and Computing, 6, 124-136. http://dx.doi.org/10.1007/s11633-009-0124-5
- 8. Andrighetto, P.L. and Bavaresco, D. (2008) Dead Zone Compensation in Pneumatic Servo Systems. ABCM Symposium Series in Mechatronics, 3, 501-509.
- 9. Recker, D.A. and Kokotovic, P.V. (1993) Indirect Adaptive Nonlinear Control of Discrete-Time Systems Containing a Deadzone. Proceedings of the 32nd Conference on Decision and Control, San Antonio, 15-17 December 1993, 2647-2653. http://dx.doi.org/10.1109/CDC.1993.325676
- 10. Zhou, J., Er, M.J. and Wen, C.Y. (2005) Adaptive Control of Nonlinear Systems with Uncertain Dead-Zone Nonlinearity. 44th IEEE Conference on Decision and Control, and the European Control Conference, Seville, 12-15 December 2005, 797-801.
- 11. Betancor-Martin, C.S., Montiel-Nelson, J.A. and Vega-Martinez, A. (2014) Deadzone Compensation in Motion Control Systems Using Model Reference Direct Inverse Control. 2014 IEEE 57th International Midwest Symposium on Circuits and Systems (MWSCAS), College Station, 3-6 August 2014, 165-168. http://dx.doi.org/10.1109/MWSCAS.2014.6908378
- 12. Jang, J.O., Chung, H.T. and Jeon, G.J. (2005) Saturation and Deadzone Compensation of Systems Using Neural Network and Fuzzy Logic. Proceedings of the 2005 American Control Conference, 3, 1715-1720. http://dx.doi.org/10.1109/ACC.2005.1470215
- 13. Chang, C.-Y., Hsu, K.-C., Chiang, K.-H. and Huang, G.-E. (2006) An Enhanced Adaptive Sliding Mode Fuzzy Control for Positioning and Anti-Swing Control of the Overhead Crane System. IEEE International Conference on Systems, Man and Cybernetics, 2, 992-997.
- 14. Kong, X.Z. and Zang, F.Y. (2009) Study on the Intelligent Hybrid Control for Secondary Regulation Transmission System. IEEE International Conference on Automation and Logistics, Shenyang, 5-7 August 2009, 726-729. http://dx.doi.org/10.1109/ICAL.2009.5262830
- 15. Bessa, W.M. and Barrêto, R.S.S. (2010) Adaptive Fuzzy Sliding Mode Control of Uncertain Nonlinear Systems. Revista Controle & Automacao, 21, 117-126.
- 16. Lewis, F.L., Tim, W.K., Wang, L.-Z. and Li, Z.X. (1999) Deadzone Compensation in Motion Control System Using Adaptive Fuzzy Logic Control. IEEE Transactions on Control Systems Technology, 7, 731-742. http://dx.doi.org/10.1109/87.799674
- 17. Jain, S. and Khorrami, F. (1995) Robust Adaptive Control of a Class of Nonlinear Systems: State and Output Feedback. Proceeding of the 1995 American Control Conference, Seattle, June 1995, 1580-1584. http://dx.doi.org/10.1109/acc.1995.529773














