Intelligent Control and Automation
Vol.5 No.1(2014), Article ID:43065,7 pages DOI:10.4236/ica.2014.51002
Hierarchical Structure of Multicriteria Problems
National Aviation University, Kiev, Ukraine
Email: alnv@voliacable.com, oberst@nau.edu.ua
Copyright © 2014 Albert N. Voronin, Yuriy K. Ziatdinov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Albert N. Voronin, Yuriy K. Ziatdinov. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 14, 2013; revised December 14, 2013; accepted December 21, 2013
KEYWORDS
Hierarchical Structure; Nested Scalar Convolutions; Multicriteria Approach; Decomposition; Composition
ABSTRACT
It is shown that any multicriteria problem can be represented by a hierarchical system of criteria. Individual properties of the object (alternative) are evaluated at the bottom level of the system, using a criteria vector. A composition mechanism is used to evaluate the object as a whole at the top level. The problem is solved by the method of nested scalar convolutions of vector-valued criteria. The methodology of the problem solving is based on the complementarity principle by N. Bohr and the theorem of incompleteness by K. Gödel. An example is presented that helps the reader digest some of the intricacies in the methodology.
1. Introduction
The problem of decision making in general view [1] can be represented by the scheme
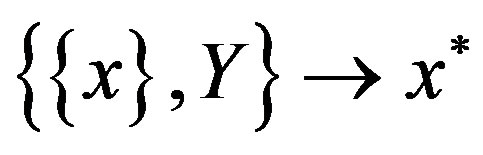 where
where 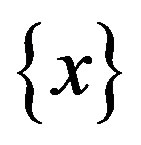 is a set of objects (alternatives);
is a set of objects (alternatives); 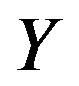 is the function of choice (rule establishing a prefer ability on a set of alternatives);
is the function of choice (rule establishing a prefer ability on a set of alternatives); 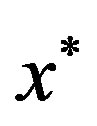 is the chosen alternatives (one or more). The set
is the chosen alternatives (one or more). The set 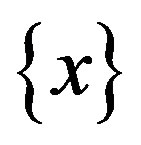 can be discrete (example: several aircraft projects from which it is necessary to choose the best) or continual (a range of radio regulator tuning from which the tuning is selected to the correct channel).
can be discrete (example: several aircraft projects from which it is necessary to choose the best) or continual (a range of radio regulator tuning from which the tuning is selected to the correct channel).
The function 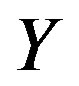 is used to solve the problem of analysis and evaluation of alternatives. On results of estimation, the choice of one or a few best alternatives from the given set follows. In decision theory, there are two different approaches to evaluating objects (alternatives) subject to choice. One of them is to evaluate an object as a whole and to choose an alternative by comparing objects as gestalts (holistic images of objects without detailing their properties). A notorious example is the estimation of an actor’s performance by K. Stanislavski: “I believe!” Obviously, a holistic approach is unabashedly subjective based on the individual preferences of the decision maker (DM) and is not quite added to formalization. There takes place a dichotomy in choosing alternatives: “like”—“do not like”. If you have a question—why do you like (or dislike), then you should use the second approach to the analysis and evaluation of alternatives.
is used to solve the problem of analysis and evaluation of alternatives. On results of estimation, the choice of one or a few best alternatives from the given set follows. In decision theory, there are two different approaches to evaluating objects (alternatives) subject to choice. One of them is to evaluate an object as a whole and to choose an alternative by comparing objects as gestalts (holistic images of objects without detailing their properties). A notorious example is the estimation of an actor’s performance by K. Stanislavski: “I believe!” Obviously, a holistic approach is unabashedly subjective based on the individual preferences of the decision maker (DM) and is not quite added to formalization. There takes place a dichotomy in choosing alternatives: “like”—“do not like”. If you have a question—why do you like (or dislike), then you should use the second approach to the analysis and evaluation of alternatives.
The second approach is detailed elaboration and assessment of various object vectors of properties and making decisions after comparing these properties. If a holistic approach implies choosing x* directly using choice function Y, the vector approach requires a mechanism to carry out decomposition of Y into a set (vector) of the choice functions y. By decomposition of the choice function, Y is understood its equivalent representation by a certain set of other functions y whose composition is the initial choice function Y.
The modern line in the theory of decision-making consists in use of the vector approach. It is explained by its objectivity and universality, and basic opportunity of application of the formalized methods. It is also taken into account concreteness and clearness of the approach, as on a narrow question there are less divergences in opinions, it is easier to collect the indisputable facts.
It is assumed that, in respect of an individual property, it is much easier to tell of which the alternatives is preferable for the decision maker. For example, in the task of selecting the best aircraft project, we can say much more confidently that the project A is better than the project B by the property of comfort, or reliability, or capacity, rather than the fact that the project A is better than the project B as a whole. Separation of properties of alternatives on the basis of the analysis is the decomposition leading to the hierarchical structure of properties. Properties of the first hierarchical level can be subdivided into the following sets of properties, etc. The dividing depth is determined by the desire to reach those properties, which are convenient for comparing with each other.
Indeed, in the example of the airplane to judge on comfort, of course, it is easier than on the airplane as a whole. But such a qualitative property is not very convenient for comparison and requires further decomposition for convenience and objectivity of properties comparison. Therefore, the comfort property, in turn, undergoes decomposition to: 1) the noise level in the cabin; 2) the level of floor vibration; and 3) the distance between the seats, etc. These characteristics are expressed in numbers and are objective.
Properties, for which there exist objective numerical characteristics, are called criteria. More rigorously: the criteria are called quantitative properties of the object, the numerical values of which are a measure of the quality assessment of the object in relation to this property. Getting a set of criteria—this is the final result of the hierarchical decomposition. The amount of levels depends on the desired depth of decomposition. The difficulty lies in the fact that, for each of the initial properties, the depth of the decomposition can be various. At each hierarchical level, it is necessary to normalize the sets of heterogeneous criteria.
The approach of comparison on separate properties, at all its attraction, derivates a serious problem of return transition to required comparison of alternatives as a whole. This problem involves the solution of the problem of criteria composition for levels of the hierarchy, which is quite difficult, especially at a considerable depth of properties decomposition. In the simplest and most widespread case (two-level hierarchy), the problem is solved in traditional form as a single scalar convolution of criteria; the numerical value of which appears as an estimate of the quality of the object (alternative) as a whole. But then in the presence of a three-level hierarchy, other approaches are required.
The foregoing gives reason to believe that any multicriteria problem can be represented by a hierarchical system, on the lower level of which the evaluation of individual properties of the object using a vector of criteria takes place, and on the upper level, through the mechanism of the composition an estimate of the object as a whole is obtained. Central here is the problem of the composition of criteria for levels of the hierarchy.
2. Statement of the Problem
Quality of an alternative is determined by hierarchical system of vectors
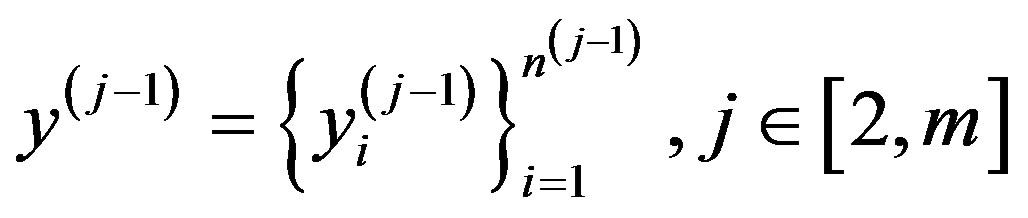 where
where 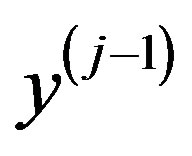 is the vector of criteria on the
is the vector of criteria on the 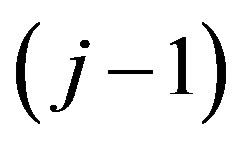 -th level of the hierarchy, by the components of which the quality of properties of alternatives for the j-th level is assessed; m is the amount of levels of the hierarchy;
-th level of the hierarchy, by the components of which the quality of properties of alternatives for the j-th level is assessed; m is the amount of levels of the hierarchy; 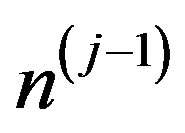 is the amount of estimated properties on
is the amount of estimated properties on 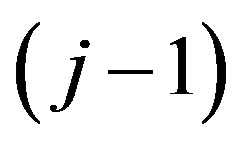 -th level of the hierarchy. The numerical values of
-th level of the hierarchy. The numerical values of 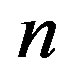 criteria
criteria 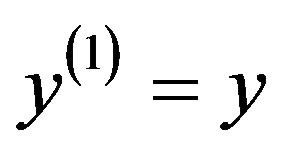 of the first level of the hierarchy for the alternative are given.
of the first level of the hierarchy for the alternative are given.
The same criterion on 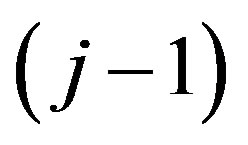 -th level can participate in the evaluation of several properties of the j-th level, i.e. in the hierarchy are possible cross-links. It is clear that
-th level can participate in the evaluation of several properties of the j-th level, i.e. in the hierarchy are possible cross-links. It is clear that
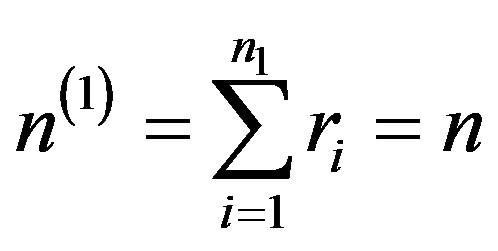 and
and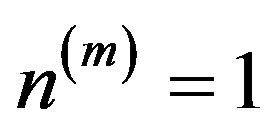 .
.
Importance (significance) of each of the components of the criterion of 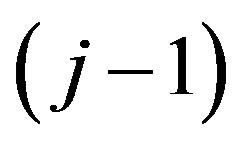 -th level in the evaluation of properties of k-th level is characterized by a property coefficient of the priority, their set forming the priority vectors system
-th level in the evaluation of properties of k-th level is characterized by a property coefficient of the priority, their set forming the priority vectors system
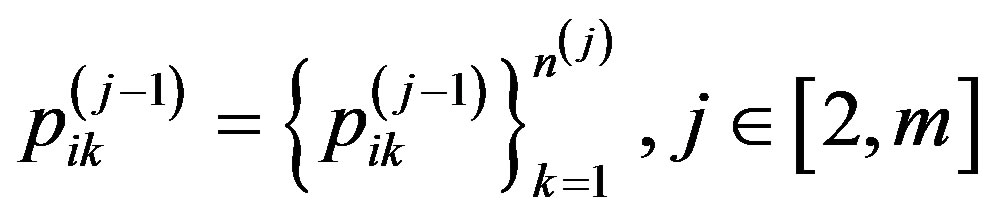 .
.
It is required to find an analytical evaluation  and qualitative evaluation of the effectiveness of this given alternative, and from the alternatives available to choose the best.
and qualitative evaluation of the effectiveness of this given alternative, and from the alternatives available to choose the best.
3. The Method of Solution
To solve this problem a systemic approach is used in which each of the alternatives (objects) is regarded as a set of elements with different (including contradictory) properties different from those of the whole system.
The complex systems situated in different conditions (situations, modes) exhibit different systemic properties, including not compatible with any of the other situations separately. At their study, the approach is used consisting in the creation and simultaneous co-existence of not one but many theoretical models of the same phenomenon, and some of them conceptually contradict each other. However, no one can be neglected, as each describes a property of the phenomenon and none can be taken as a single because it does not express the full range of its properties. Compare the said with the principle of complementarity, introduced into science by Niles Bohr: “... To reproduce the integrity of the phenomenon should be used mutually exclusive “complementary” classes of concepts, each of which can be used in its own, special conditions, but only when taken together, exhaust the definable information.” For a complete description of the object they are equally necessary and therefore do not contradict, but complement each other.
Multiple properties of a complex system in a given situation of its functioning are evaluated quantitatively by relevant partial criteria. In different situations, the rank “most important” acquires different properties and, consequently, different partial criteria. Thus, mutually exclusive “complementary” classes of concepts which appear as individual theoretical models are characterized by partial contradictory criteria, each of which is most useful in its own, special conditions. It is the principle of complementarity that allows for separating and then linking these criteria in multicriteria evaluation. Only a full set of individual criteria (vector criterion) enables an adequate assessment of the functioning of a complex system as a manifestation of the contradictory unity of all its properties.
However, this possibility represents only a necessary but not a sufficient condition for the vector evaluation of the entire alternative as a whole. Indeed, let it be that at the lower level of the hierarchy of criteria the numerical values of partial criteria of comfort properties of aircraft are known, such, as the distance between the seats, the noise level in the cabin, the amplitude of the vibration of the floor, etc. Does it mean that we, knowing these values, can estimate the property of comfort as a whole? No, we cannot.
It is appropriate to recall the old Indian parable about the blind men who wished to become familiar with an elephant. One touched the trunk and decided that the elephant is similar to a snake. The second picked up the ear and told that the elephant reminds to him a bed-sheet. The third felt the leg and declared that the elephant is a pole. These individual elephant “models” reflect the various properties of the object, but do not give the whole picture.
For a complete evaluation it is necessary to go out from the lower level of the hierarchy and to rise on the following tier, i.e. to carry out an act of criteria composition. Let’s compare this with the incompleteness theorem of Kurt Gödel “... In every complex enough not contradictory theory of the first order there is a statement, which by means of the theory is impossible neither to prove, nor to deny. But the self-consistency of a particular theory can be established by means of another, more powerful formal theory of the second order. But then the question of the self-consistency of this second theory arises, and so forth.” We can say that Gödel’s theorem is a methodological basis for the study of hierarchical structures.
With reference to our problem it means that for an adequate estimation of an alternative as a whole we should solve a task of the criteria composition on levels of hierarchy, consecutively passing from the bottom level up to top.
4. The Scalar Convolution of Criteria
A scalar convolution of criteria can serve as a tool for the act of composition. The scalar convolution—it is a mathematical technique for data compressing and quantifying its integral properties by a single number.
The most widely used is an additive (linear) scalar convolution
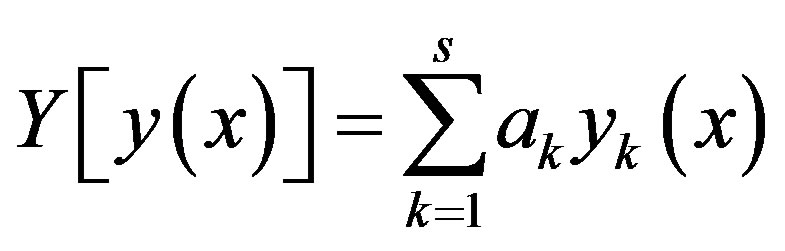 where
where 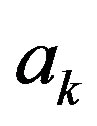 are the weight coefficients; s is the amount of individual criteria. The principle of Laplace in the theory of decision-making consists in extremization of linear scalar convolution. The shortcoming (specificity) of use of linear scalar convolution is the possibility of “indemnification” of one criterion at the expense of others.
are the weight coefficients; s is the amount of individual criteria. The principle of Laplace in the theory of decision-making consists in extremization of linear scalar convolution. The shortcoming (specificity) of use of linear scalar convolution is the possibility of “indemnification” of one criterion at the expense of others.
Multiplicative convolution
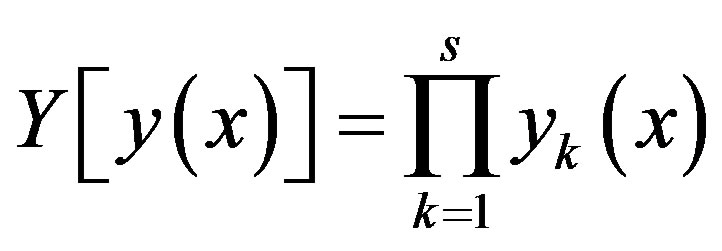
is free from these drawbacks. Pascal’s principle is an extremalization of the scalar multiplicative convolution.
Historically, the principle of Blasé Pascal’s first set out in the “Pensees”, published in 1670; it is believed that this work has laid the foundation of the whole theory of decision making. Here are introduced two key concepts of the theory: 1) the individual criteria, each of which assesses the effectiveness of one or another side of the decision, and 2) the principle of optimality, i.e., rule allowing on the values of criteria to calculate a single numerical measure of the effectiveness of the decision.
The disadvantage of use of a scalar multiplicative convolution is that a very expensive and very effective system may have the same score as a cheap and low effective system. Let’s compare such “weapons systems”, as the atomic bomb and the slingshot, which at low cost has a certain damaging factor. Guided by the multiplicative convolution, you have a risk to choose to equip the army with a slingshot.
The principle of guaranteed result leads to the Chebyshev scalar convolution
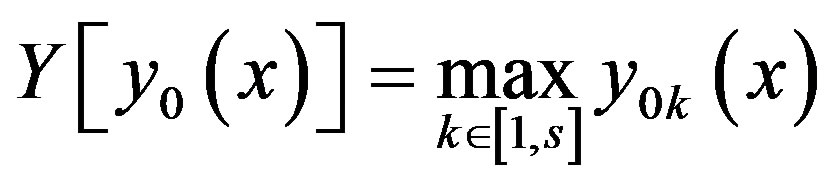 where
where 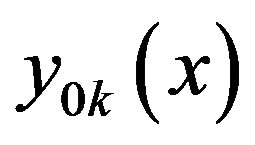 are normalized (reduced to unity) partial criteria. This convolution is used under conditions of uncertainty, and also in those cases when the subjects to minimization partial criteria are dangerously approaching their limiting values (restrictions).
are normalized (reduced to unity) partial criteria. This convolution is used under conditions of uncertainty, and also in those cases when the subjects to minimization partial criteria are dangerously approaching their limiting values (restrictions).
Convolution on the Charnes-Cooper concept. The concept is based on the principle “closer to the ideal (utopian) point”. In the space of criteria under specified conditions and restrictions an apriori unknown ideal vector 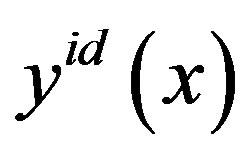 is determined, for which the optimization problem is solved s times (the amount of individual criteria), each time with one (just another) criterion, as if the others were not exist at all. The sequence of “onecriterion” solutions of the initial multicriteria problem gives the coordinates of the unattainable ideal vector
is determined, for which the optimization problem is solved s times (the amount of individual criteria), each time with one (just another) criterion, as if the others were not exist at all. The sequence of “onecriterion” solutions of the initial multicriteria problem gives the coordinates of the unattainable ideal vector
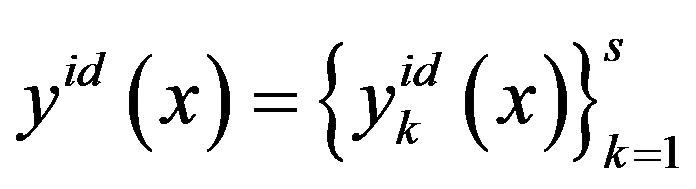 .
.
Thereafter, the scalar convolution 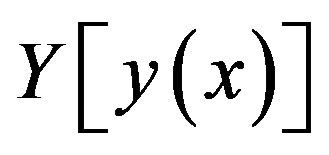 is introduced as a measure of approximation to the ideal vector in the space of criteria in the form of a non-negative function of the vector
is introduced as a measure of approximation to the ideal vector in the space of criteria in the form of a non-negative function of the vector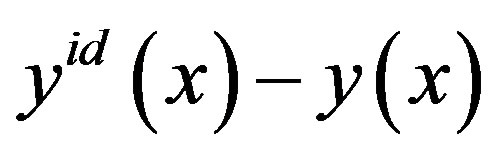 , e.g. in the form of a square of the Euclidean norm of the vector
, e.g. in the form of a square of the Euclidean norm of the vector
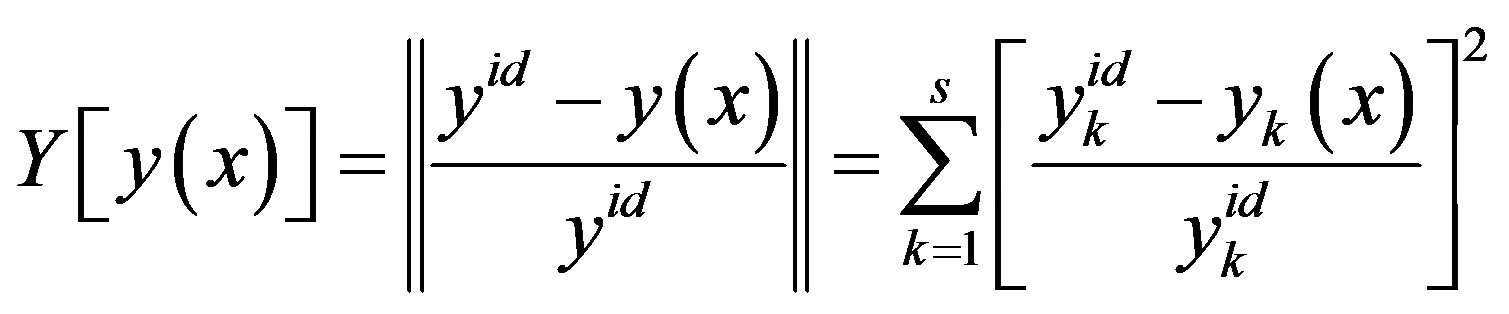 .
.
The disadvantage of this method is cumbersome procedure for determining an ideal vector coordinates.
In [2], a scalar convolution on nonlinear compromise scheme for the criteria subject to be minimized is proposed
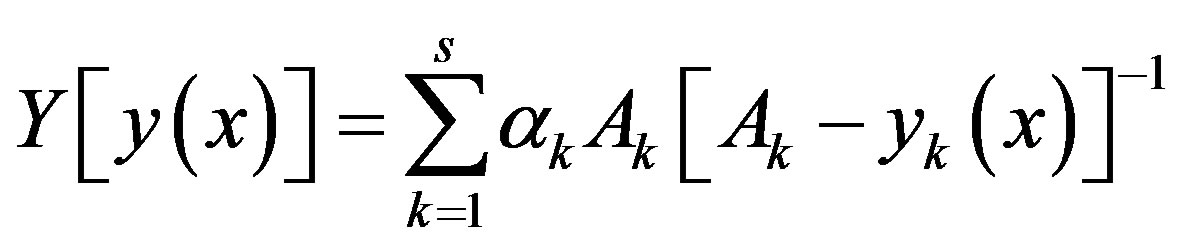 applied in cases where the decision-maker considers as the preferred those solutions in which the values of individual criteria
applied in cases where the decision-maker considers as the preferred those solutions in which the values of individual criteria 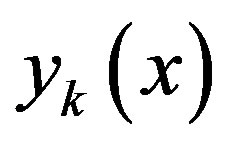 are farthest from their limit values,
are farthest from their limit values,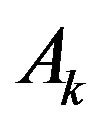 . This convolution has a number of essential advantages, which include flexibility, universality and analyticity.
. This convolution has a number of essential advantages, which include flexibility, universality and analyticity.
The choice of a compromises scheme is made by the DM and appears as explicitly conceptual.
In the problem of making the choice the amount of variants (alternatives) is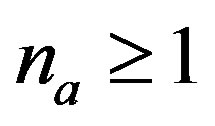 . Each variant is characterized by its own hierarchical structure. If
. Each variant is characterized by its own hierarchical structure. If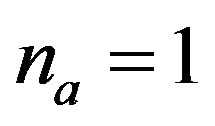 , the problem is transformed to the task of evaluation of this given hierarchical structure. If
, the problem is transformed to the task of evaluation of this given hierarchical structure. If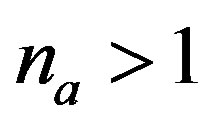 , each structure is estimated as a given and is chosen that option, the hierarchical structure of which obtained the best estimate. Therefore, when a discrete multiobjective optimization takes place, as a basic here the problem of estimating a given hierarchical structure is considered. However, we do so only in the case of a relatively small amount of alternatives
, each structure is estimated as a given and is chosen that option, the hierarchical structure of which obtained the best estimate. Therefore, when a discrete multiobjective optimization takes place, as a basic here the problem of estimating a given hierarchical structure is considered. However, we do so only in the case of a relatively small amount of alternatives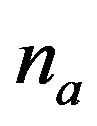 , when the method of simple enumeration does not cause significant computational difficulties. When large volumes of sets of alternatives take place, we should employ other methods of optimization, such as described in [2].
, when the method of simple enumeration does not cause significant computational difficulties. When large volumes of sets of alternatives take place, we should employ other methods of optimization, such as described in [2].
Evaluation of this given alternative is nothing else but a solution of the problem of analysis of the alternative quality under a given argument 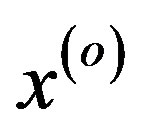 from the set
from the set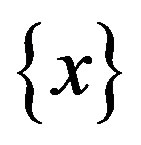 . This enables henceforth in the expressions of criteria to not include the values of the argument x.
. This enables henceforth in the expressions of criteria to not include the values of the argument x.
5. Nested Scalar Convolutions
It is proposed for analytical evaluation of hierarchical structures to apply a method of nested scalar convolutions [2]. The composition is performed on the “matryoshka principle”: the scalar convolutions of the weighted components of vector criteria of lower level serve as the components of the vectors of higher level criteria. Scalar convolution of criteria obtained at the uppermost level is automatically considered as the expression for the analytical evaluation of effectiveness of the entire hierarchical system.
The algorithm for nested scalar convolutions is represented by an iterative sequence of operations of the weighed scalar convolutions of criteria for each level of the hierarchy from the bottom up, taking into account the priority vectors, based on the selected compromise scheme
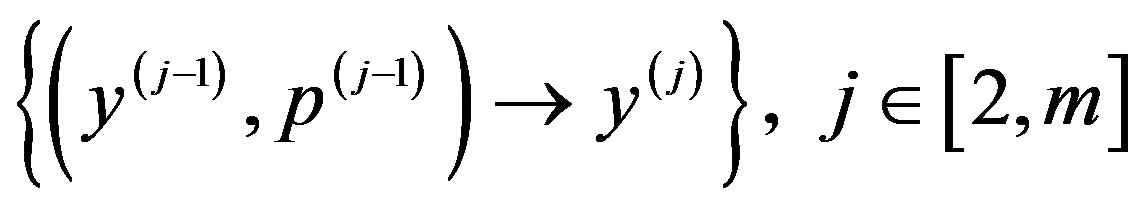 (1)
(1)
and the searching and evaluating of effectiveness of the entire hierarchical system (alternative) as a whole is expressed by the problem of determining the scalar convolution of criteria on the top level of the hierarchy:
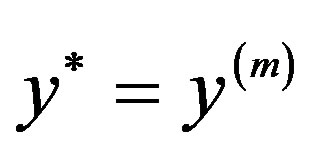 .
.
when using the recurrent formula (1) important is the rational choice of the compromise scheme. For the method of nested scalar convolutions the adequate is a nonlinear compromise scheme, as described in [2]. It is established that, without loss of generality, a premise for its use is that all the partial criteria were non-negative, were subject to minimization and were limited:
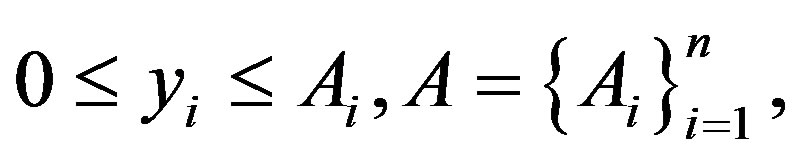
where A is the vector of restrictions on the criteria of the current level of the hierarchy; n is the amount of them.
Proceeding from (1) the expression to evaluate k-th property of an alternative for the j-th level of the hierarchy by using the nonlinear compromise scheme looks like
 (2)
(2)
where criteria of the 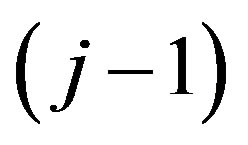 -th level are normalized (redu-ced to unity). Thus,
-th level are normalized (redu-ced to unity). Thus, 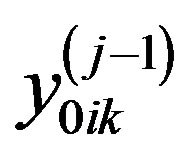 are the normalized vector’s
are the normalized vector’s 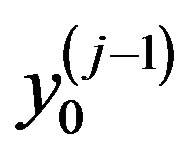 components involved in the evaluation of properties of the k-th alternative on the j-th level of the hierarchy;
components involved in the evaluation of properties of the k-th alternative on the j-th level of the hierarchy; 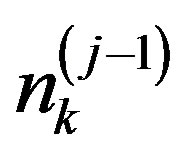 is their amount;
is their amount; 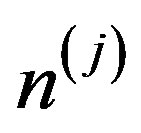 is the amount of evaluated properties of the j-th level.
is the amount of evaluated properties of the j-th level.
6. Calculation of the Priority Coefficients
Coefficients of priority 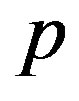 are the formal parameters with dual physical meaning. On the one hand, they are priority coefficients expressing the preferences of individual decision-makers concerning certain criteria. On the other – they are the regression coefficients of the model constructed on the basis of the concept of nonlinear compromise scheme. Determination of the coefficients
are the formal parameters with dual physical meaning. On the one hand, they are priority coefficients expressing the preferences of individual decision-makers concerning certain criteria. On the other – they are the regression coefficients of the model constructed on the basis of the concept of nonlinear compromise scheme. Determination of the coefficients 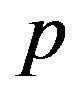 at each level of the hierarchy can be done by optimizing on the simplex (3) using a dual approach described in [2], or by expert analysis using an ordinal (serial) or a cardinal (interval) scale.
at each level of the hierarchy can be done by optimizing on the simplex (3) using a dual approach described in [2], or by expert analysis using an ordinal (serial) or a cardinal (interval) scale.
In the latter case, the decision maker or expert should assess the relative influence of each partial criterion of the lower-level of hierarchy on the overall assessment of the k-th alternative properties at the next level in the given conditions, and relate this assessment with the corresponding point on the rating scale, characterized by the number f. Experts can select the point between numbers or assign several criteria to one point on the scale.
The domain of the coefficients of priority 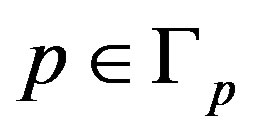 is a simplex
is a simplex
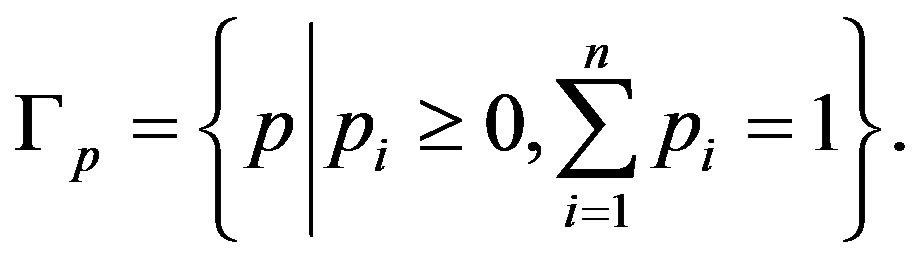 (3)
(3)
This normalization is performed, if the coefficients of priority are determined by the formula
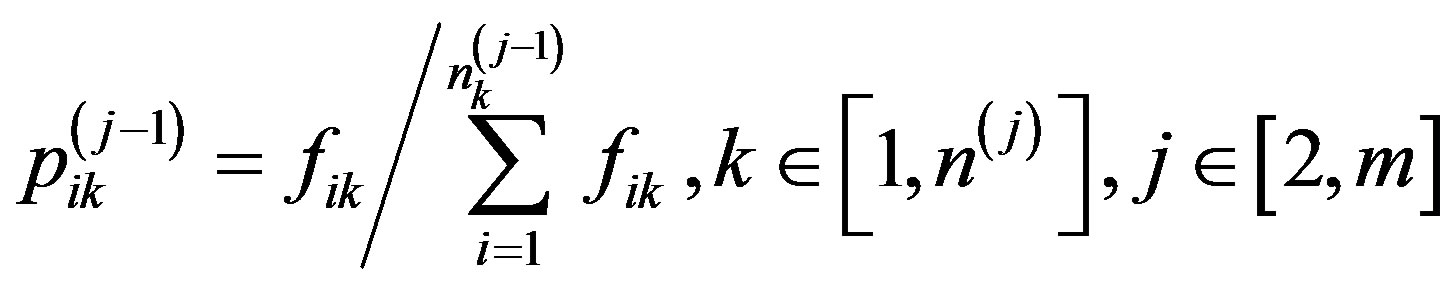
where 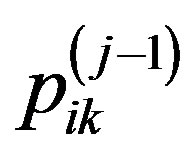 is the i-th component of the priority vector for
is the i-th component of the priority vector for  -th level of the hierarchy in the calculation of evaluation of the k-th property effectiveness on a j-th level;
-th level of the hierarchy in the calculation of evaluation of the k-th property effectiveness on a j-th level; 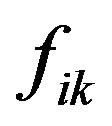 is assessment of the importance of i-th property on
is assessment of the importance of i-th property on 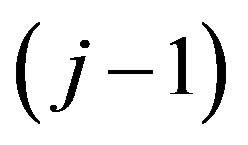 level for the k-th property on j-th level (is determined by experts or decision-makers on the rating scale). If several experts take part in the evaluation procedure, the estimates
level for the k-th property on j-th level (is determined by experts or decision-makers on the rating scale). If several experts take part in the evaluation procedure, the estimates  can be obtained either by a simple arithmetic averaging of experts estimates (when the level of expert’s competence is about the same), or according to their competence in this matter. The procedure for calculation of competence coefficients is described in [2].
can be obtained either by a simple arithmetic averaging of experts estimates (when the level of expert’s competence is about the same), or according to their competence in this matter. The procedure for calculation of competence coefficients is described in [2].
It’s more complicated procedure when an expert estimates the coefficients of the priority on ordinal scales, in other words, is ranking criteria in their order of importance. Rank—it is a natural number that characterizes the serial number of criteria. The result of the expert’s work is represented by a rank sequence of j-th expert:
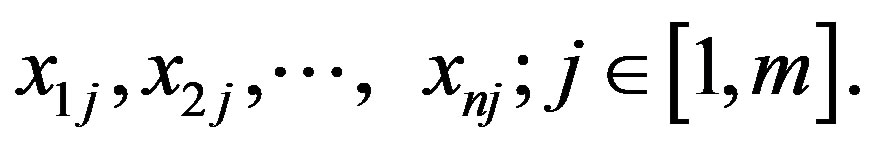
Here, 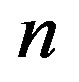 is the amount of criteria; m is the amount of experts.
is the amount of criteria; m is the amount of experts.
As the experts’ evaluations are given in ordinal scale, the arithmetic averaging method cannot be applied. To construct the group opinion of experts in this case a ranks finite-dimensional space is introduced and metrics in it. A ranking of the j-th expert is a point 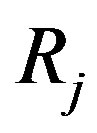 in ranks space. The metric
in ranks space. The metric 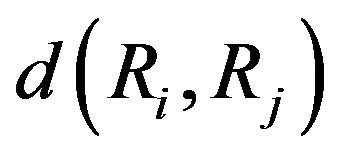 represents the distance between the rankings i and j.
represents the distance between the rankings i and j.
To calculate the rank of the i-th criterion the Kemeny median (group expert opinion) is used. This is such a point in the space of ranks, that the sum of distances between it and all other points is minimal:
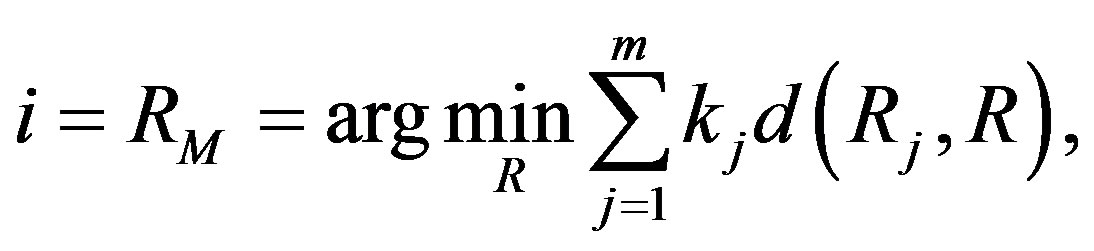
where 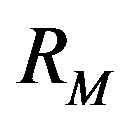 is the median or the generalized Kemeny ranking for the i-th criterion;
is the median or the generalized Kemeny ranking for the i-th criterion; 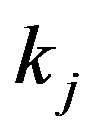 is the coefficient of competence of j-th expert (determined by known methods [2]); R is the current ranking, in which the minimization takes place. The metric
is the coefficient of competence of j-th expert (determined by known methods [2]); R is the current ranking, in which the minimization takes place. The metric 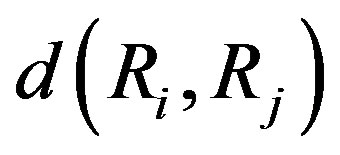 is chosen as
is chosen as
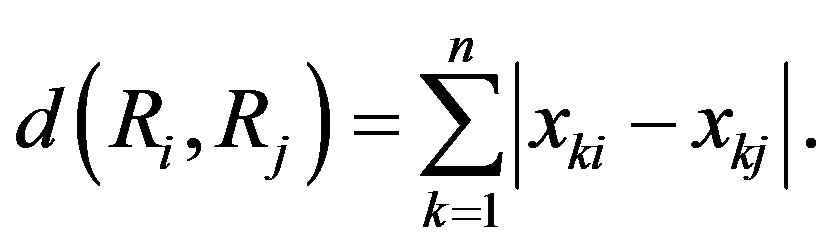
Calculating the Kemeny median—this is a problem of integer programming. To solve it the different algorithms of discrete mathematics are used, for example, based on the branch and bound method.
Based on the generalized ranking the weighting coefficient for each criterion can be determined, using a Fishburne scale [3]:
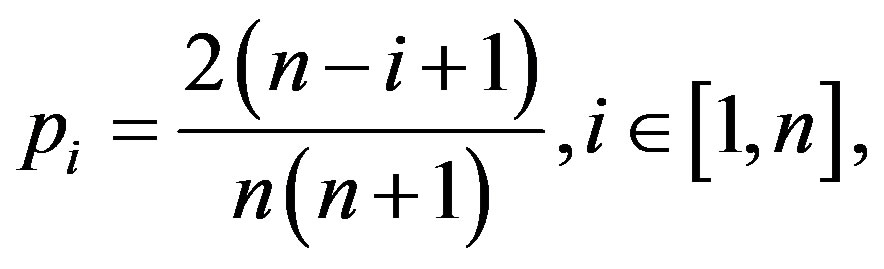
where 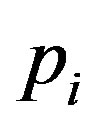 is the significance coefficient of i-th criterion;
is the significance coefficient of i-th criterion; 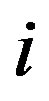 is the rank of the current criterion in the generalized ranking; n is the amount of criteria.
is the rank of the current criterion in the generalized ranking; n is the amount of criteria.
We can see that the priority coefficients calculation is a daunting task, especially when you use the ranking methods.
In the most simple and rather common case the multicriteria problem is formulated and solved without priorities, when decision-makers believe that all the importance parameters for all properties of alternatives are the same. In this case, a simple scalar convolution with the nonlinear trade-offs scheme in a unified form is used [2].
7. The Recurrent Formula for Calculating the Criteria
In order to formula (2) reflected the idea of the nested scalar convolutions method in accordance with the recurrent relation (1), this expression should be normalized, i.e., must be obtained a relative measure such that it were subject to be minimized, and it were the unit for it as the limit value.
The structure of the nonlinear compromise scheme enables normalizing the convolution (2) not to the maximum (which in this case is difficult), but to the minimum value of criteria convolution. Indeed, the ideal values for the criteria that are subject to be minimized are their zero points. Putting in (2)
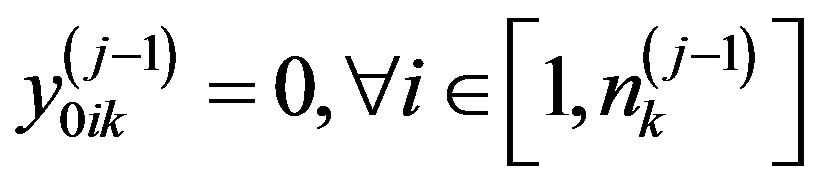
and taking into account the normalization (3), we obtain
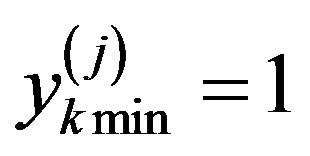 . After calculations [2], the final expression for the recurrent formula for calculating analytical assessments of the alternatives properties at all levels of the hierarchy becomes
. After calculations [2], the final expression for the recurrent formula for calculating analytical assessments of the alternatives properties at all levels of the hierarchy becomes
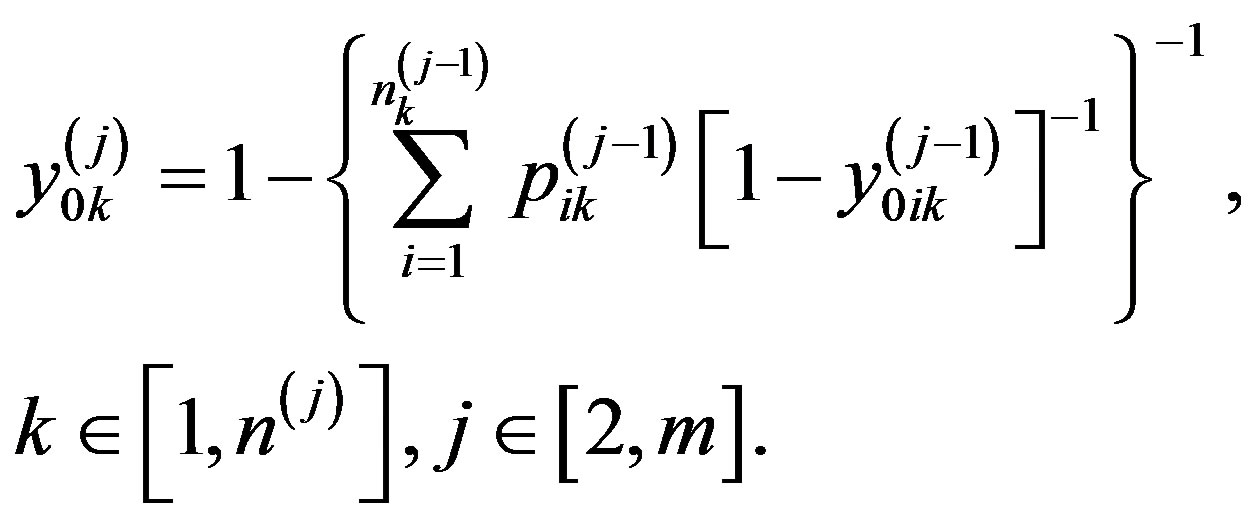 (4)
(4)
8. Qualitative Evaluation of Alternatives
A qualitative (linguistic) estimate is obtained by comparing the analytic evaluation of an alternative with the inverse normalized fundamental scale. The general concept of an ordinal fundamental scale is described in [4]. An interval normalized inverted scale is presented by the Table 1. It shows the relationship between qualitative gradations of properties of objects and the corresponding normalized quantitative estimates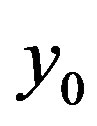 .
.
We can say that in terms of the theory of fuzzy sets [4], the fundamental scale acts as a universal membership function for the transition from the digital quantity to the appropriate quality grading and back. The transition from the linguistic variable estimate (“satisfactory quality, high quality, etc.) to the appropriate quantitative estimates on the rating scale is carried out, i.e. a transition from fuzzy quality grades to numbers and vice versa takes place.
Evaluating variants using a unified normalized fundamental scale makes it possible to solve multicriteria problems both in traditional formulations and in the case where an alternative should be selected from a set of inhomogeneous alternatives, for which a unified set of quantitative assessment criteria cannot be formulated, and to estimate the unique alternative [5].
9. Illustrative Example
Suppose you want to find a quantitative  and
and
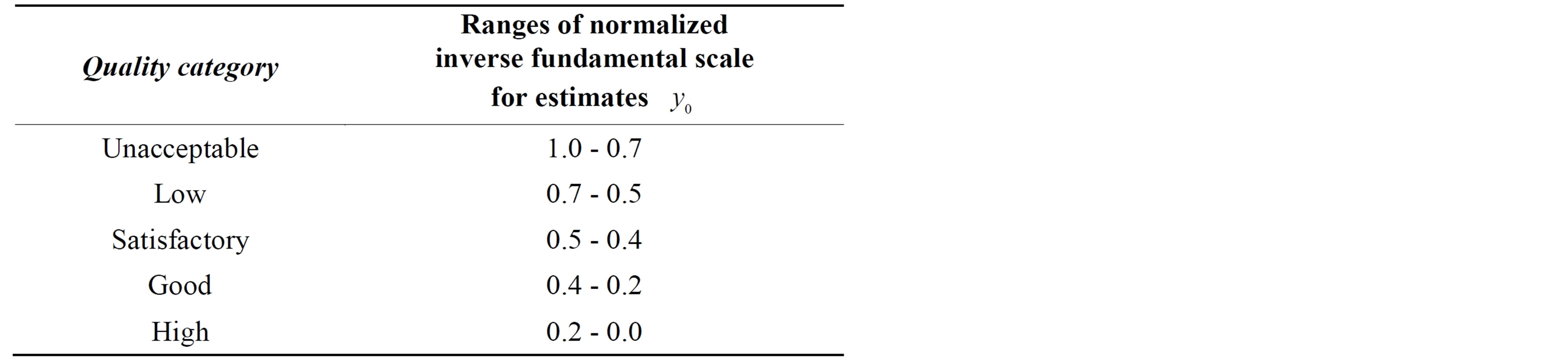
Table 1. A normalized inverted scale.
qualitative evaluation of aircraft project for two main characteristics: comfort, characterized by the as yet unknown evaluation criterion 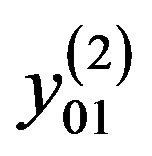 and reliability, which is mapped as yet unknown evaluation criterion
and reliability, which is mapped as yet unknown evaluation criterion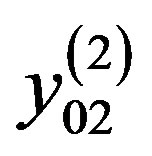 . Comfort property, in turn, is estimated according to three criteria: the distance between the seats in the passenger cabin
. Comfort property, in turn, is estimated according to three criteria: the distance between the seats in the passenger cabin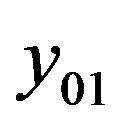 , the noise level in the cabin
, the noise level in the cabin 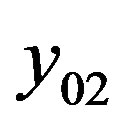 and the level of vibration in the cabin floor
and the level of vibration in the cabin floor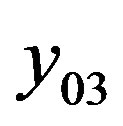 . Reliability is estimated by probability of equipment failures
. Reliability is estimated by probability of equipment failures 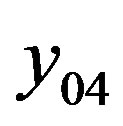 and structural strength
and structural strength . Apart from these two in the evaluation of the reliability criterion is involved the level of vibration in the cabin floor
. Apart from these two in the evaluation of the reliability criterion is involved the level of vibration in the cabin floor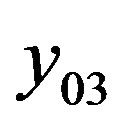 , i.e. there is a crossconnection. All the above criteria are normalized and reduced to the same method of extremization, namely, they are subject to minimization. The criteria of the lower level participate in the evaluation of the properties of the highest level, with priority coefficients
, i.e. there is a crossconnection. All the above criteria are normalized and reduced to the same method of extremization, namely, they are subject to minimization. The criteria of the lower level participate in the evaluation of the properties of the highest level, with priority coefficients
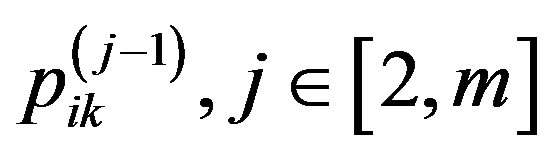 .
.
The following numeric values are given. Criteria of lower (first) hierarchy level:
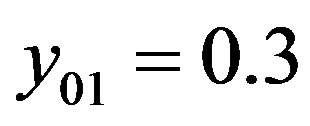 ,
, 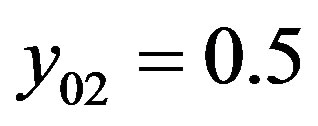 ,
, 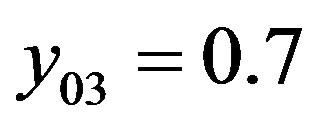 ,
, 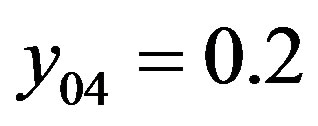 ,
,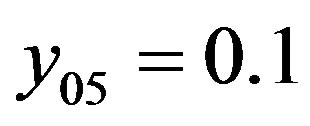 .
.
Priority coefficients:
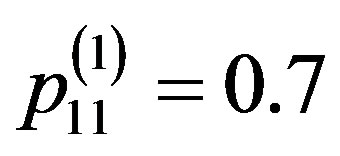 ,
, 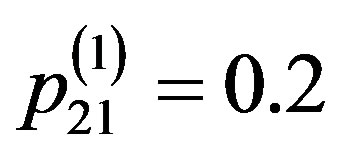 ,
,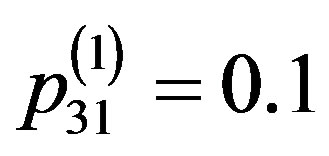 ,
, 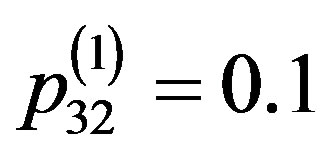 ,
,  ,
, 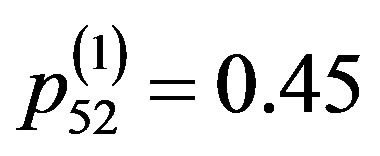 ,
, 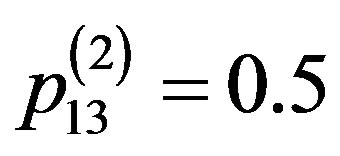 ,
,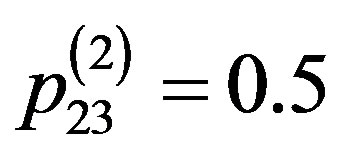 .
.
At the first stage of criteria composition, based on the recurrent formula (4), we obtain an expression for the analytic evaluation of comfort property (second level of the hierarchy):
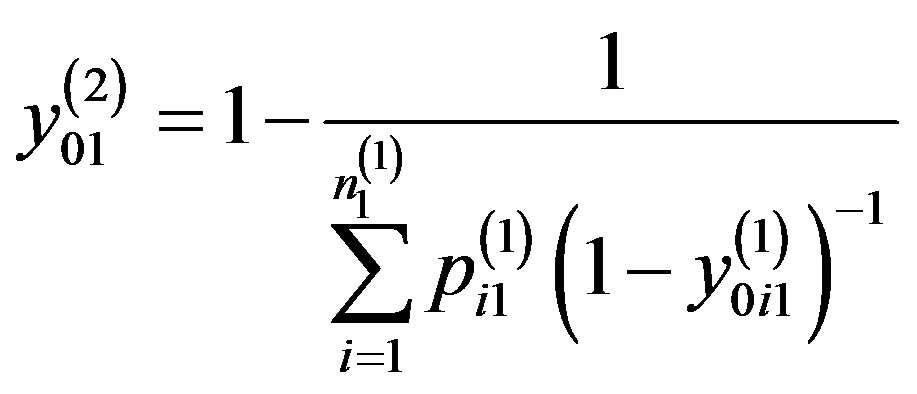 where
where 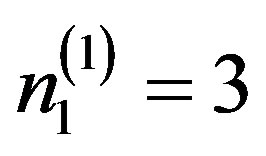 and
and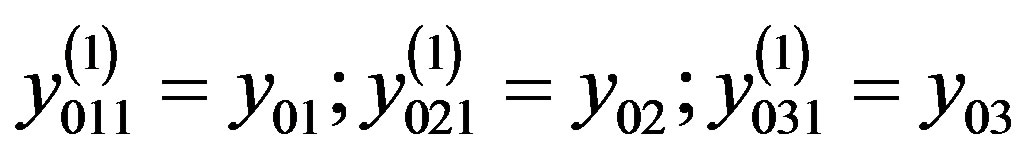 .
.
Substituting numeric values, we get
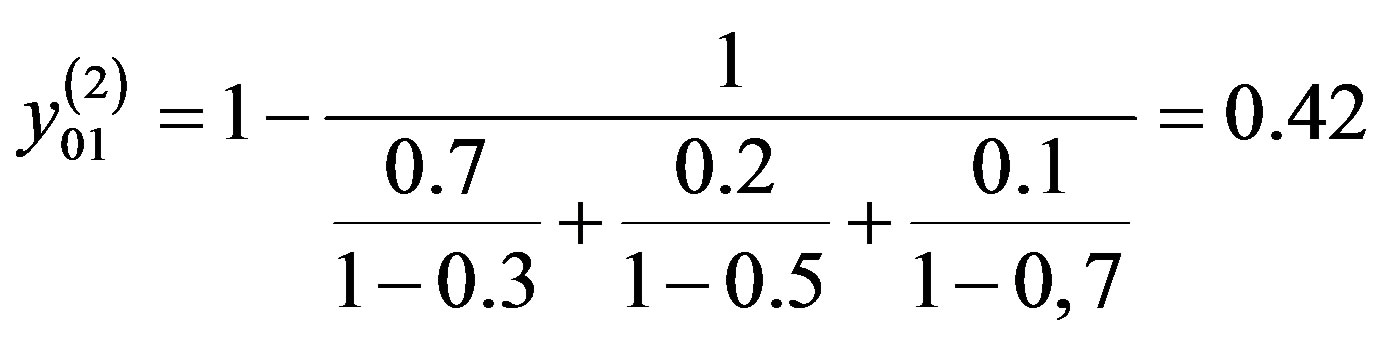
Comparing this with the analytic assessment of the Table 1, we find that the comfort property of the aircraft project quality is satisfactory.
An analytic expression for the evaluation the reliability property (also the second level of the hierarchy) has the form
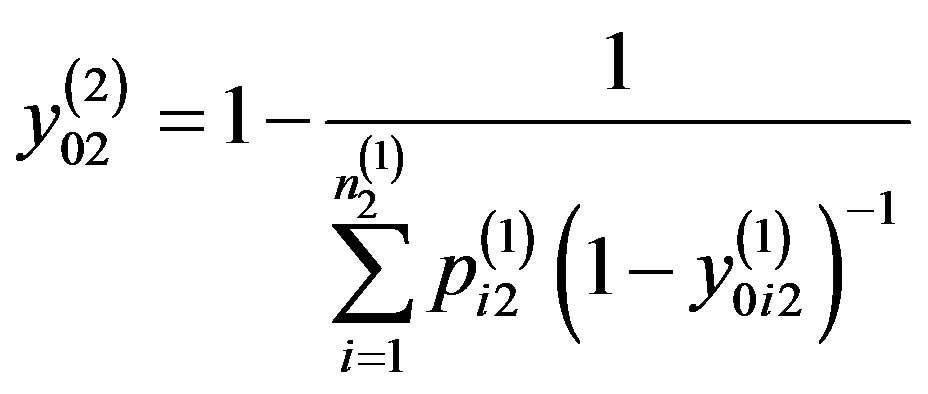 where in with the cross-connection
where in with the cross-connection 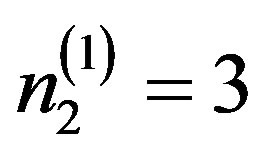 and
and
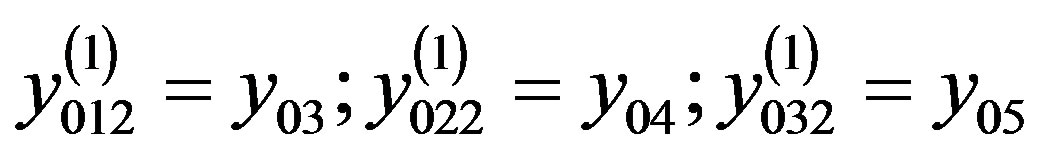 .
.
Priority coefficients: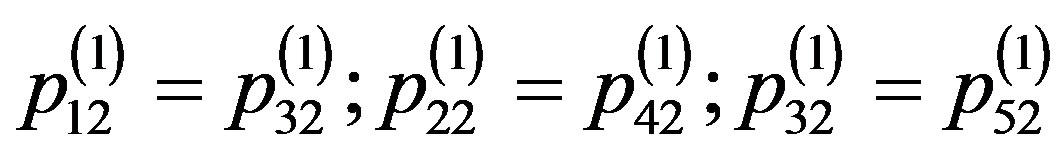 .
.
Substituting the numeric values, we obtain
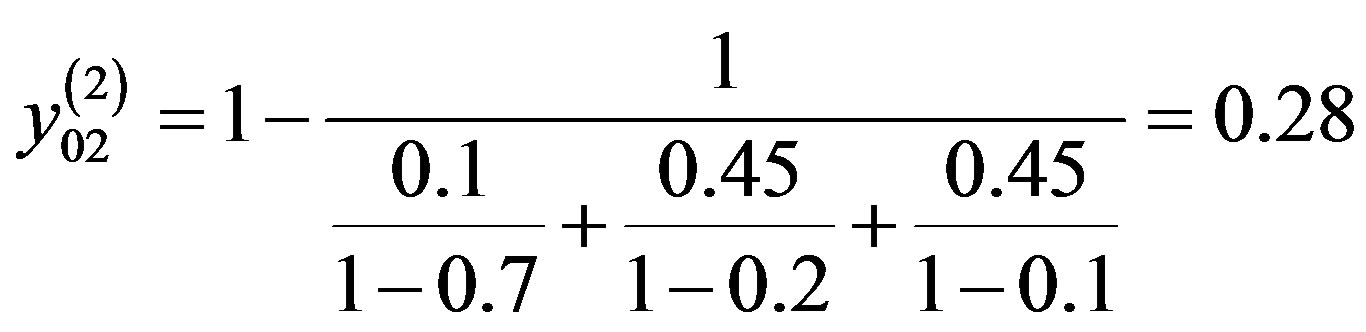 .
.
According to Table 1, the quality of the reliability property of this project is estimated as high.
At the final (second) stage of criteria the composition formula (4) takes the form
 where
where 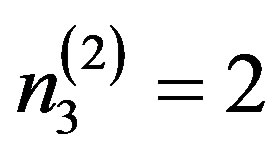 and
and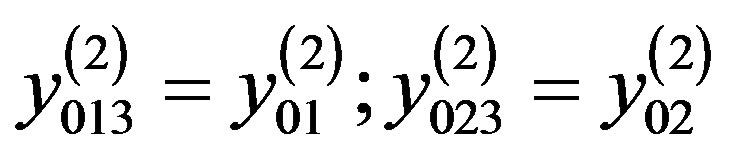 .
.
Substituting the numerical values, we get
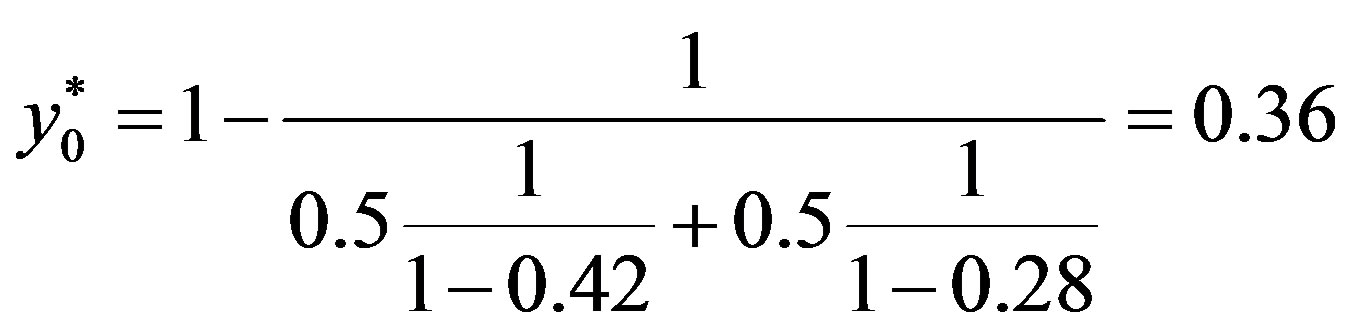
Table 1 shows that with this analytic assessment of the aircraft project its quality as a whole is evaluated as good.
10. Conclusions
The foregoing leads to the conclusion that any problem of the vector assessment of an alternative can be represented by a hierarchical system of criteria, resulting from the decomposition of an alternative property. The lower level of the hierarchy is an object (alternative) assessment on selected properties, using initial criteria vector. The upper level is obtained through the mechanism of the composition as a whole object evaluation. Central here is the problem of the composition of criteria for levels of the hierarchy to be solved by the method of nested scalar convolutions.
The methodological basis of an alternative properties decomposition to obtain the initial criteria vector is the Bohr’s principle of complementarity. This is a necessary condition for vector estimation of alternatives.
The methodology of a criteria composition for levels of the hierarchy is based on the Gödel’s theorem of incompleteness. This is a sufficient condition for vector estimation of alternatives.
We dare say that, above inferences about notions of criteria, decomposition and composition can be extended on the more general notions of analysis and synthesis.
REFERENCES
- V. A. Gubanov, V. V. Zakharov and A. N. Kovalenko, “Introduction to Systems Analysis,” [in Russian], Leningrad State University, Leningrad, 1988.
- A. N. Voronin, Ju. K. Ziatdinov and M. V. Kuklinsky, “Multicriteria Decisions: Models and Methods,” [in Russian], NAU, Kiev, 2011.
- P. Fishburne, “Utility Theory for Decision Making,” [in Russian], Nauka, Moscow City, 1978.
- T. L. Saaty, “Multicriteria Decision Making: The Analytical Hierarchy Process,” McGraw-Hill, New York, 1990.
- A. N. Voronin, “The Method of Multicriteria Evaluation and Optimization of Hierarchical Systems,” [in Russian], Cybernetics and Systems Analysis, No. 3, 2007, pp. 84-92.

