Intelligent Control and Automation
Vol.4 No.2(2013), Article ID:31732,4 pages DOI:10.4236/ica.2013.42017
ISPO: A New Way to Solve Traveling Salesman Problem
1College of Science, China University of Mining & Technology, XuZhou, China
2Foundation Departments, Xuzhou Air Force Academy, XuZhou, China
Email: plaxz@126.com
Copyright © 2013 Xiaohua Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 24, 2012; revised January 15, 2013; accepted January 23, 2013
Keywords: Mobile Operators; Particle Swarm Optimization; Traveling Salesman Problem
ABSTRACT
This paper first introduces the concepts of mobile operators and mobile sequence, with which it redefines the rate of particle swarm optimization algorithm and the formula of position updating. Combining this discrete PSO algorithm with neighbors, the paper puts forward Hybrd Particle Swarm Optimization Algorithm, whose effectiveness is verified at the end of this paper.
1. Introduction
The Particle Swarm Optimization algorithm [1] presented by psychologists Kennedy and Dr. Eberhart in 1995 is a new intelligent optimization algorithm which imitated the behaviors of birds. Compared with others, the PSO has shown its advantages. The PSO is intuitive and easy to realize and has high efficiency in complement. Nowadays, the PSO is widely used in many fields, such as functions optimization, training of neutral network, Fuzzy system control and so on.
Traveling salesman problem (TSP) is a typical combinatorial optimization problem, which may be described as follows. Given n cities and the distances between every two cities, which is the shortest path for travelling all the cities only once?
At first, PSO algorithm as an efficient method is mainly used to solve some continuous optimization problems. However, with the development of PSO algorithm, some experts and scholars began to think how to solve the discrete optimization problems, such as, Kennedy [2] proposed a discrete PSO algorithm used to solve binary problems in the year of 1997 and he proposed a dynamic probabilistic PSO in 2005 [3]. In addition, some scholars presented the discrete PSO algorithm for solving TSP problem. Clerc [4] re-explained the velocity and position equation through replacement sequence, and Huang [5] proposed swapping sequence. Others combined crossover and mutation of genetic algorithm with PSO algorithm [6], Zeng and Cui presented a new unified model of PSO [7] which can be used in solving combinatorial optimization problem. This paper proposed mobile operators and mobile sequence for solving TSP problem. The arrangement of this paper is as follows. In Section 2, mobile operators and mobile sequence were defined. In Section 3, the velocity and position equation of PSO were re-explained and PSO algorithm was improved base on simulated annealing algorithm. In Section 4, TSP examples were used to evaluate the improved PSO algorithm, and the conclusions are given in Section 5.
2. Mobile Operators and Mobile Sequence
Definition 1. Assuming the solution space of TSP with n nodes be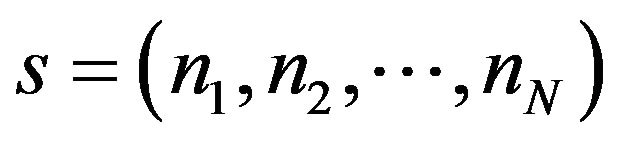 ,
,  , and the mobile operator sv(i,k) means the node ni of s moving k steps
, and the mobile operator sv(i,k) means the node ni of s moving k steps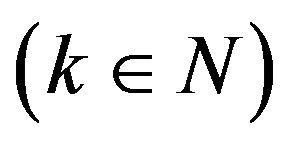 . If k is greater than zero, node ni moves backward, on the contrary, it moves forward, and it keeps unmovable if k equals to zero. The formula
. If k is greater than zero, node ni moves backward, on the contrary, it moves forward, and it keeps unmovable if k equals to zero. The formula 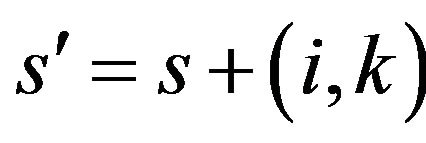 is a new solution after processing by the mobile operator sv(i,k). And the symbol plus is given a new meaning. Because the result of solving TSP is an h-cycle, and
is a new solution after processing by the mobile operator sv(i,k). And the symbol plus is given a new meaning. Because the result of solving TSP is an h-cycle, and 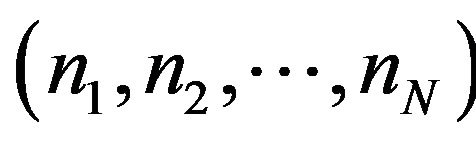 and
and  are the same solution actually.
are the same solution actually.
If k is greater than zero, node ni moves k steps anticlockwise, otherwise it moves |k| steps clockwise.
Example 1. Assuming there are five nodes in TSP, and s equals to (1, 2, 3, 4, 5), the mobile operator is sv(1,2), and s’ can be presented as follows:
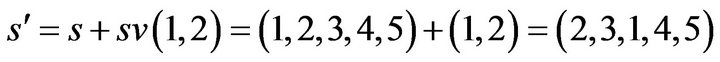
If the mobile operator is sv(3,3), thus
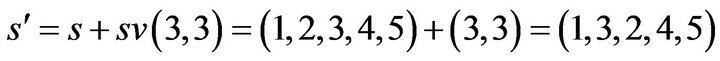
Definition 2. Mobile sequence is the ordered sequence of one or more mobile operators, and it can be expressed as follows:

where  are mobile operators, and the order of each operators has the rigorous significance.
are mobile operators, and the order of each operators has the rigorous significance.
A mobile sequence is running on a TSP’s solution which means all operators of the mobile sequence are running on the solution one by one.
Definition 3. Various mobile sequences running on one solution could bring same solution, all mobile sequences set with the same running result is called mobile sequences’ equivalent set.
Definition 4. More than one mobile sequence can be combined into a new sequence,  is defined as the combining operator of two mobile sequences.
is defined as the combining operator of two mobile sequences.
Definition 5. Assuming a mobile sequence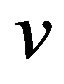 , which is made up of n mobile operators, equals to
, which is made up of n mobile operators, equals to  , the length of this mobile sequence
, the length of this mobile sequence  is defined as n, i.e. the number of mobile operators. If
is defined as n, i.e. the number of mobile operators. If  is one,
is one, 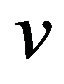 is called unit mobile sequence.
is called unit mobile sequence.
Definition 6. Let 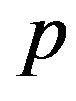 be a real coefficient on the interval (0,1) and v be a mobile sequence and it equals to
be a real coefficient on the interval (0,1) and v be a mobile sequence and it equals to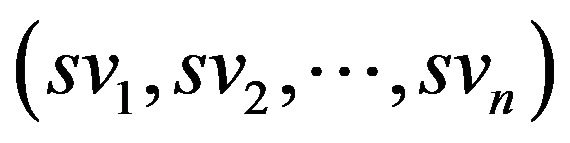 ,
, 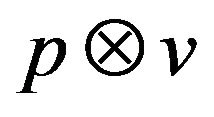 is defined by
is defined by
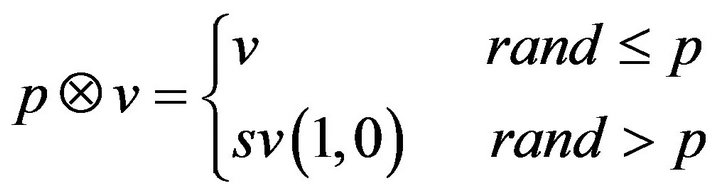
where rand is a random number between 0 and 1. It means, 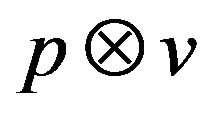 equals to
equals to 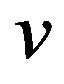 on probability
on probability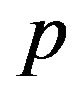 .
.
3. IPSO—Improved PSO Algorithm
Now, we can rewrite the iterative formula of PSO algorithm as follows:
 (1)
(1)
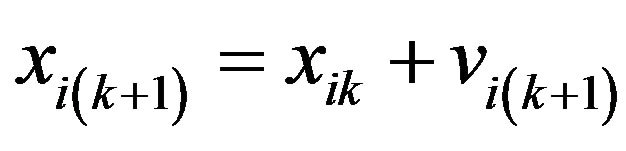 (2)
(2)
where
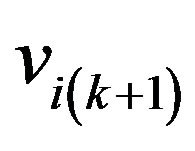 := velocity of particle i at time step k + 1,
:= velocity of particle i at time step k + 1,
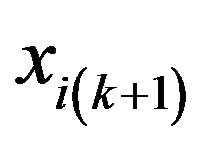 := position of particle i at time step k + 1,
:= position of particle i at time step k + 1,
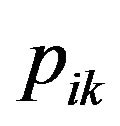 := best previous position of particle i, found so far, at time step k,
:= best previous position of particle i, found so far, at time step k,
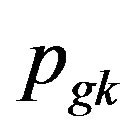 := best neighbor’s previous best position, at time step k ,
:= best neighbor’s previous best position, at time step k ,
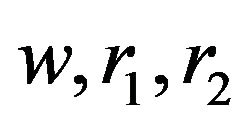 := social/cognitive confidence coefficients, and
:= social/cognitive confidence coefficients, and  are random numbers between 0 and 1.
are random numbers between 0 and 1.
As the PSO algorithm is easily trapped into local optimum in dealing with continuous problems, this paper applies the hybrid algorithm based on PSO to solve the TSP to avoid the same trouble. In each iteration, the PSO algorithm is running firstly, then produces l new positions in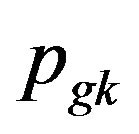 ’s neighborhoods by using the simulated annealing (SA) algorithm, compares the fitness of l positions’ and
’s neighborhoods by using the simulated annealing (SA) algorithm, compares the fitness of l positions’ and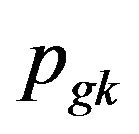 ’s, chooses the best position as
’s, chooses the best position as 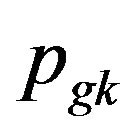 and assigns the new position of
and assigns the new position of  to a particle as the first particle which is randomly selected. If the same solution is got in m times of iterations, the velocity of all particles must be re-initialized.
to a particle as the first particle which is randomly selected. If the same solution is got in m times of iterations, the velocity of all particles must be re-initialized.
The specific process of the improved algorithm is shown as follows:
1. Initialize the position and velocity of particle swarm, define velocity of each particle as the mobile sequence, and calculate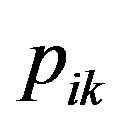 ,
,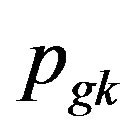 ;
;
2. Update particles’ velocity and position according to Formulas (1) and (2) shown before;
1) Calculate the difference between 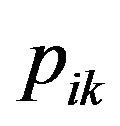 and
and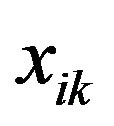 , and assign the result to A. A represent a mobile sequence which runs on
, and assign the result to A. A represent a mobile sequence which runs on  and obtain
and obtain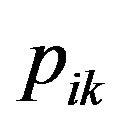 . Then calculate
. Then calculate  and renew A with the result;
and renew A with the result;
2) Calculate the difference between  and
and , and assign the result to B. B represent a mobile sequence which runs on
, and assign the result to B. B represent a mobile sequence which runs on  and obtain
and obtain . Then calculate
. Then calculate  and renew B with the result;
and renew B with the result;
3) Calculate 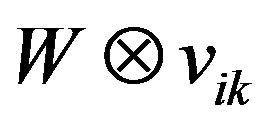 and plus with A and B, then renew particle’s velocity with the result;
and plus with A and B, then renew particle’s velocity with the result;
4) Update particle’s position according to Formula (2);
3. Renew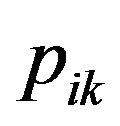 ,
,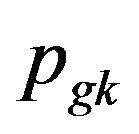 ;
;
4. Generate  new locations randomly in the neighborhoods of
new locations randomly in the neighborhoods of , compare the fitness of the new locations with
, compare the fitness of the new locations with . Renew
. Renew  and assign it to the first particle;
and assign it to the first particle;
5. Determine whether the algorithm has found the same optimal value after m times’ iteration, if the answer is yes, re-initialize all particle’s velocity.
6. Determine whether the stop condition is met. If it’s met, end the loop, otherwise, go to Step 2.
4. Experiments
The weight of inertia of PSO is linear, which can be expressed as follows:
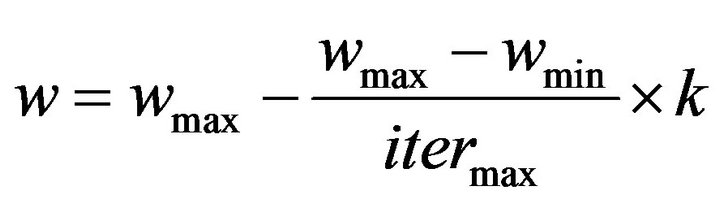
where
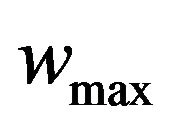 := Initial weight
:= Initial weight
 := final weight
:= final weight
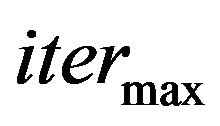 := the maximum number of iterations
:= the maximum number of iterations
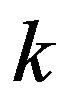 := the current number of iterations TSP with 14 nodes [4,8] is used to examine the effectiveness of the improved algorithm. Parameters setting: n-the number of particles is 40, the maximum times of iteration is 1000. The length of all particles’ velocity is initialized to 1 randomly, and the value of m is 10 as well as l. Weight initialization:
:= the current number of iterations TSP with 14 nodes [4,8] is used to examine the effectiveness of the improved algorithm. Parameters setting: n-the number of particles is 40, the maximum times of iteration is 1000. The length of all particles’ velocity is initialized to 1 randomly, and the value of m is 10 as well as l. Weight initialization: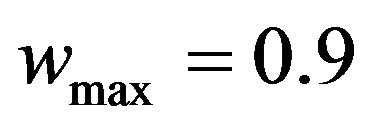 ,
,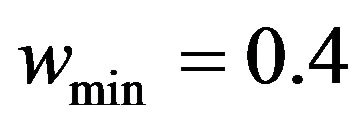 . All feasible solution sequence begins from the first node. We executed the algorithm randomly for 30 times, the results of the experiments are analyzed in the Table 1.
. All feasible solution sequence begins from the first node. We executed the algorithm randomly for 30 times, the results of the experiments are analyzed in the Table 1.
The maximum search space of the improved PSO algorithm is 50,000.The search space of [8] is 200000 and is 4 times of ours, which shows that our approach is more effective. And in all the 30 runs our approach has consistently found the optimal solution, which presents our algorithm convergence rate is 100 percent.
Swapping sequence 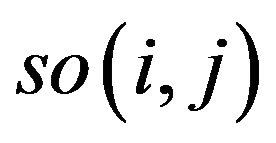 is proposed in references 4, which means exchanging
is proposed in references 4, which means exchanging 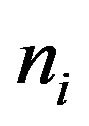 with
with 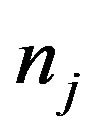 in the solution sequence
in the solution sequence . Now, compare swapping sequence
. Now, compare swapping sequence 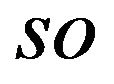 with mobile sequence
with mobile sequence . If A is (1 2 3 4 5 6 7), and B is (1 3 4 5 6 2 7), then
. If A is (1 2 3 4 5 6 7), and B is (1 3 4 5 6 2 7), then 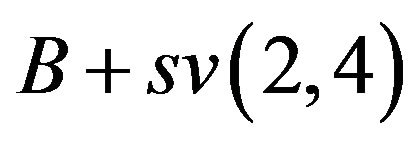 equals to A,
equals to A,

equals to A. Normally, unit mobile sequence 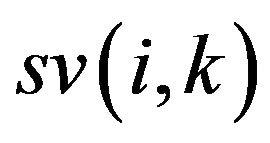 is equivalent to swapping sequence
is equivalent to swapping sequence

of length k when 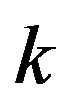 is greater than zero and
is greater than zero and 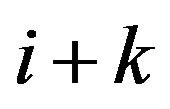 is not greater than N. On the contrary, if
is not greater than N. On the contrary, if 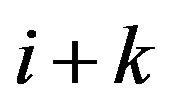 is greater than N, it can be converted into a swapping sequence
is greater than N, it can be converted into a swapping sequence  of length
of length . Furthermore, unit swapping sequence
. Furthermore, unit swapping sequence  (if j is greater than i) can be converted into a mobile sequence
(if j is greater than i) can be converted into a mobile sequence

of length two, if j equals to I + 1, it can be converted into the unit mobile sequence . All of these imply that all problems the swapping sequence solved can be solved by mobile sequence, too. According to the length of exchange, mobile sequence has the advantage on swapping sequence. Moreover, if we take the definition
. All of these imply that all problems the swapping sequence solved can be solved by mobile sequence, too. According to the length of exchange, mobile sequence has the advantage on swapping sequence. Moreover, if we take the definition

Table 1. Results of TSP (14 nodes).
of swapping sequence into consideration, it has no identical operator, which means there is no unit swapping sequence  can support the equation:
can support the equation: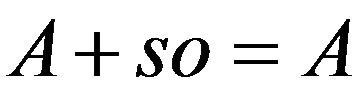 . However, the mobile sequence can overcome the shortcoming of swapping sequence with the equation
. However, the mobile sequence can overcome the shortcoming of swapping sequence with the equation  is satisfied in all solution sequence. Therefore mobile sequence is more effective than swapping sequence.
is satisfied in all solution sequence. Therefore mobile sequence is more effective than swapping sequence.
For further verification of performance of improved algorithm, we apply the improved algorithm to solving Bays 29 [9] and Oliver 30 [10]. The data come from TSPLIB, the weight decreases from 0.9 to 0.4 during the iteration and the maximum times of iteration is 1500, and other parameters are as same as TSP with 14 nodes. All experiments independently run 30 times and the results are shown in Table 2 and the best solutions of the two plans are shown in Figures 1 and 2.
From Table 2, it is obvious that the improved algorithm gets a high convergence rate either in Bays 29 or in
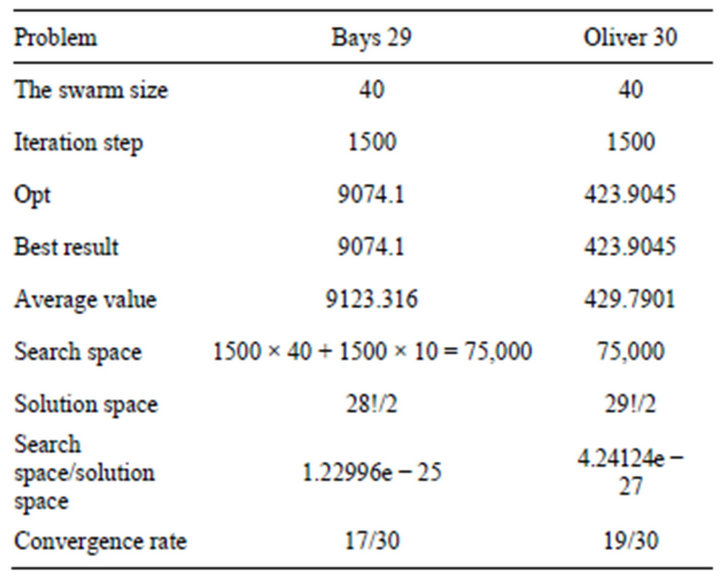
Table 2. Results of experiments Bays 29 and Oliver 30.
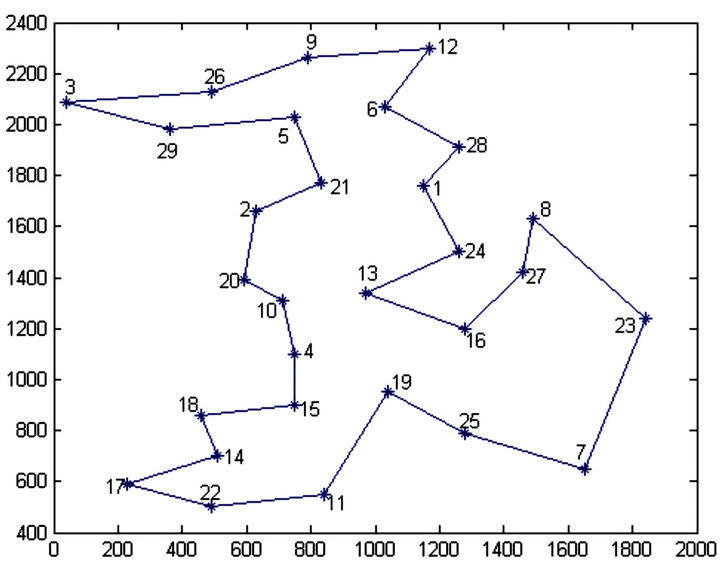
Figure 1. The best solution of experiment BAYS 29 with our algorithm.
Oliver 30, though the search space versus solution space is small (1.22996e−25, 4.24124e−27). It demonstrates that the improved algorithm has the advantages of small searching area and high convergence rate in solving the small TSP problems, and it is efficient.
For comparison, three other artificial algorithms including basic SA, basic GA and Basic Ant Colony Algorithm are used to solve the same TSP problem. All four algorithms are run 20 times for Oliver30, the results are shown in Table 3.
Form Table 3, it is clear that our algorithm is better than the other algorithms. For Oliver 30 problem, our improved PSO not only can achieve the best fitness value 423.7405 but also the average fitness value is better than the other algorithm’s. This means our improved PSO is a better and more effective means to solve TSP problem.
5. Conclusions
This paper has improved the PSO algorithm by introducing the concepts of mobile operator and mobile sequence. The improved algorithm can be applied to solve discrete

Figure 2. The best solution of experiment Oliver 30 with our algorithm.

Table 3. Results for Oliver30 problem.
problems. Through experiments in this paper, we can draw conclusions:
1) Using PSO algorithm with mobile operators and mobile sequence is an effective new way to solve TSP.
2) The improved algorithm has the advantages in small searching area and high convergence rate in solving the small TSP problems.
REFERENCES
- J. Kennedy and R. C. Eberhart, “Particle Swarm Optimization,” IEEE International Conference on Neural Network, Perth, 1995, pp. 1942-1948.
- J. Kennedy and R. C. Eberhart, “A Discrete Binary Version of the Particle Swarm Algorithm,” Proceedings of the World Multiconference on Systemics, Cybernertics and Informatics 1997, IEEE Service Center, Piscataway, 1997, pp. 4104-4109.
- J. Kennedy, “Dynamic-Probabilistic Particle Swarms,” Proceedings of the Genetic and Evolutionary Computation Conference, Washington DC, 2005, pp. 201-207.
- M. Clerc and J. Kennedy, “The Particle Swarm-Explosion, Stability and Convergence in a Multidimensional Complex Space,” IEEE Transactions on Evolutionary Computation, Vol. 6, No. 1, 2002, pp. 58-73. doi:10.1109/4235.985692
- L. Huang, K.-P. Wang and C.-G. Zhou, “Particle Swarm Optimization for Traveling Salesman Problems,” Journal of Jilin University, Vol. 41, No. 4, 2003, pp. 477-480.
- S. Gao, B. Han, X. J. Wu, et al., “Solving Traveling Salesman Problem by Hybrid Particle Swarm Optimization Algorithm,” Control and Decision, Vol. 19, No. 11, 2004, pp. 1286-1289.
- J. C. Zeng and Z. H. Cui, “A New Unified Model of Particle Swarm Optimization and Its Theoretical Analysis,” Journal of Computer Research and Development, Vol. 43, No. 1, 2006, pp. 96-100. doi:10.1360/crad20060115
- L.-P. Fang, P. Chen and S.-H. Liu, “Particle Swarm Optimization with Simulated Annealing for TSP,” Proceeding of the 6th WSEAS International Conference on Artificial intelligence, Knowledge Engineering and Data Bases, Corfu Island, 2008.
- Y. Marinakis and M. Marinaki, “A Hybrid Multi-Swarm Particle Swarm Optimization algorithm for the Probabilistic Traveling Salesman Problem,” Computers & Operations Research, Vol. 37, No. 3, 2010, pp. 432-442. doi:10.1016/j.cor.2009.03.004
- C. Wang, M. M. Zeng and J. Li, “Solving Traveling Salesman Problems with Time Windows by Genetic Particle Swarm Optimization,” 2008 IEEE Congress on Evolutionary Computation, 2008, pp. 1752-1755.

