Intelligent Control and Automation
Vol. 3 No. 1 (2012) , Article ID: 17564 , 4 pages DOI:10.4236/ica.2012.31002
Study on Complex System Evaluation Method Based on PCA and Grey Relative Degree
1Northwestern Polytechnical University, Xi’an, China
2Institute of Underwater Vehicle, Northwestern Polytechnical University, Xi’an, China
Email: jiangjun@nwpu.edu.cn
Received October 25, 2011; revised November 24, 2011; accepted December 1, 2011
Keywords: Complex System; Systemic Evaluation; PCA; Grey Relative Degree
ABSTRACT
The complexity and limited data samples in evaluation of complex system are obstacles for traditional evaluation method. Based on Grey relative degree theory and principal components analysis (PCA) method, a novel systemic evaluation method is put forward in this paper. Firstly, standardization method is modified for evaluation objective, and the method includes expression (2) and (3). Secondly, for few schemes of complex system, grey relative degree, expression (5), is substituted for relation coefficient. At last, validity of the method is verified by evaluating 3 schemes of a type of UUV.
1. Introduction
At present, along with the development of science and technology, most of objectives we deal with, whose fundamental properties include otherness, diversity, pertinence and whole property, are relative to lots of factors. So, complex system and relative theories and methods have been widely used in our society, commerce, research, and so on. At the same time, it is important to estimate and evaluate complex system, because there are many applications of complex systems ineffective, and some complex systems did not achieve the desired results and caused the user heavy losses, which had seriously affected the development of complex systems. As a result, it is necessary for the research of evaluation methods which could provide a theoretical basis for development of complex system. However, evaluation methods for complex systems have been greatly improved under the more attention of researchers, such as “integrated score”, “cost-benefit analysis”, “analytic hierarchy process”, “data envelopment analysis”, “fuzzy comprehensive evaluation”, “grey relative analysis” and so on. However, there are some shortages in the current evaluation methods, especially all of them do not consider the complexity and limited data samples of complex system [1,2]. The complexity of complex system includes multitudinous indices, nonlinear relationship among indices. Principal component analysis (PCA) has been widely used to evaluate complex system, and achieved good effect. But, due to relation coefficient method is based on quantity data, traditional PCA could not deal with limited data accurately, especially small sample data.
In this paper, a novel complex system evaluation method is put forward based on principal component analysis (PCA) and Grey relative degree. PCA is a method for reducing the space dimension of samples and delete redundant information. And grey relative degree is introduced to deal with small sample data instead of relative coefficient method.
2. Method of Evaluation
Principal component analysis is one of multivariate analysis techniques, and it is an efficient method for the high dimensional, correlated input space into the appropriate lower dimensional subspace. In the input data space, PCA searches for directions with the biggest data variations, provided that these directions are orthogonal, and uses them as a primary axis of a new coordinate system in which the input space is then projected [3]. Thereby PCA transforms correlated variables into the set of new uncorrelated variables which are called principal components (PCs).
2.1. Standardization of Data
By taking a number of the production process data at the normal operating conditions, a data matrix X(xij)  Sm×n can be created for the process variable. In which each column corresponds to a set of variables (as the sample point data at the same scheme), each row corresponds to a sample (as a variable values at different schemes). That is to say, m is the number of indices of complex system, n is the number of schemes of complex system.
Sm×n can be created for the process variable. In which each column corresponds to a set of variables (as the sample point data at the same scheme), each row corresponds to a sample (as a variable values at different schemes). That is to say, m is the number of indices of complex system, n is the number of schemes of complex system.
2.1.1. Score Method
Usually, for lots of data of a variable, the standardization method is based on Score method [4-6]. That is,
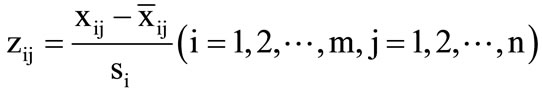 (1)
(1)
where, 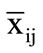 is the mean value of the ith variable data, and si is the covariance of the ith variable data.
is the mean value of the ith variable data, and si is the covariance of the ith variable data.
It is obvious that the accuracy of si depends on the numbers of data. However, for complex system evaluation, the number of system schemes is small, and, although expression (1) considers data of the variable, it is not concern of relationship between evaluation objective and the variable. So, it is not suitable for evaluating complex system.
2.1.2. Standardization for Objective
For the evaluation objective of complex system, the categories of indices are two kinds: cost and benefit type. So, considering the evaluation objective, a new standardization method is presented,
1) Cost type variable
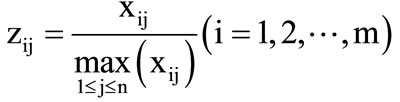 (2)
(2)
2) Benefit type variable
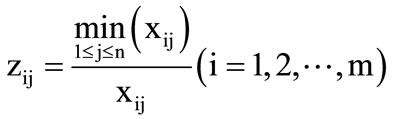 (3)
(3)
The standardization matrix is Z(zij) ∈ Sm×n.
2.2. Coefficient Matrix
2.2.1. Correlation Matrix
According to the standardization matrix Z, a correlation matrix R(rij) can be created. It has contained the correlation degree between all the measured variables. rij expresses the correlation degree between the ith variable and the jth variable. That’s,
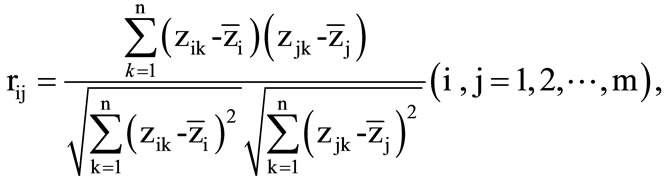 (4)
(4)
where,  is the mean value of the ith variable standard data.
is the mean value of the ith variable standard data.
It is obvious that the accuracy of correlation degree is direct to the amount of data. That is to say, the more is the amount of schemes, the more is accuracy of the evaluation result for complex system.
2.2.2. Grey Relative Degree Matrix
Grey relation analysis is considered to be an analysis of the geometric proximity between different discrete sequences within a system. The proximity is described by the grey relative degree, which is regarded as a measure of the similarities of discrete data that can be arranged in sequential order.
Assumption sequences:
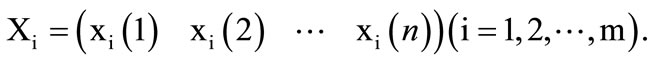
Then, the grey relative degree of Xi and Xj is (5):
where,  is of the distinguished coefficient. A value of
is of the distinguished coefficient. A value of  is the smaller and the distinguished ability is the larger,
is the smaller and the distinguished ability is the larger, 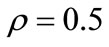 generally.
generally.
The eigenvalues of matrix R are 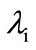
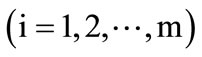 , and
, and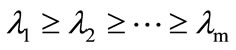 .
.
Thus, a transformation matrix P can be obtained by the following equation:
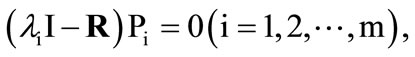
where, Pi is the eigenvector of the matrix R corresponding to the eigenvalue, .
.
2.3. Principle Components
The number of principal component should be determined by calculating the variance contribution rate. If the number of the principal component was selected as k, then the information which contain in the measured variables can be obtained by calculating the variance contribution rate.
 (6)
(6)
The principal component model can be defined as:
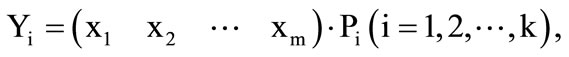 (7)
(7)
where, xi is the ith variable of complex system.
2.4. PCA Evaluation Model
PCA integrated output can be defined as:
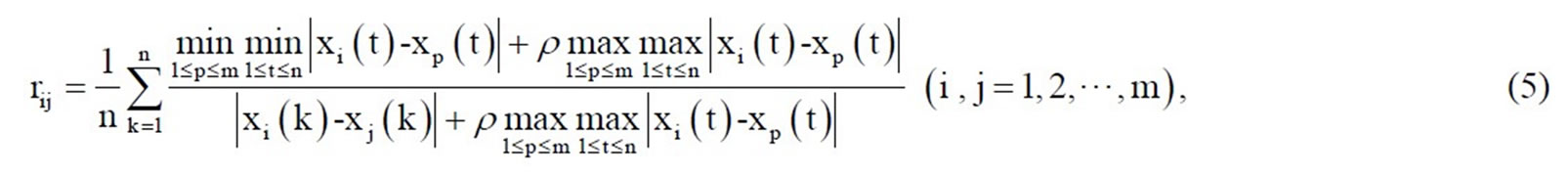
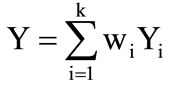 (8)
(8)
where, wi is the variance contribution rate of the princepal components in the PCA evaluation model, is given by
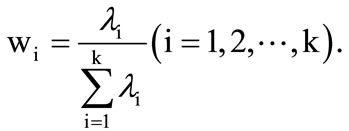
3. Application and Analysis
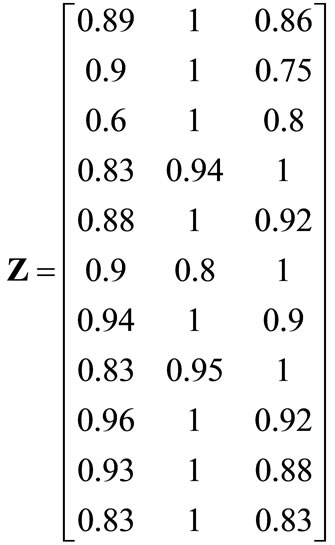
For example, there are 3 schemes (A1,A2,A3) of unmanned underwater vehicle (UUV) to be evaluated. 11 attributes should be considered, which are listed in Table 1. x1 is MTBF, x2 is range, x3 is navigation depth, x4 is navigation velocity, x5 is recognition angle, x6 is searching distance, x7 is anti-jamming probability, x8 is radius of load action, x9 is the load capability, x10 is gyroidal radius of trajectory, x11 is MTTR.
For the evaluation objective, x10 and x11 belong to cost type attribute, others belong to benefit type attribute.
According to expressions (2) and (3), the standardizetion matrix Z is:
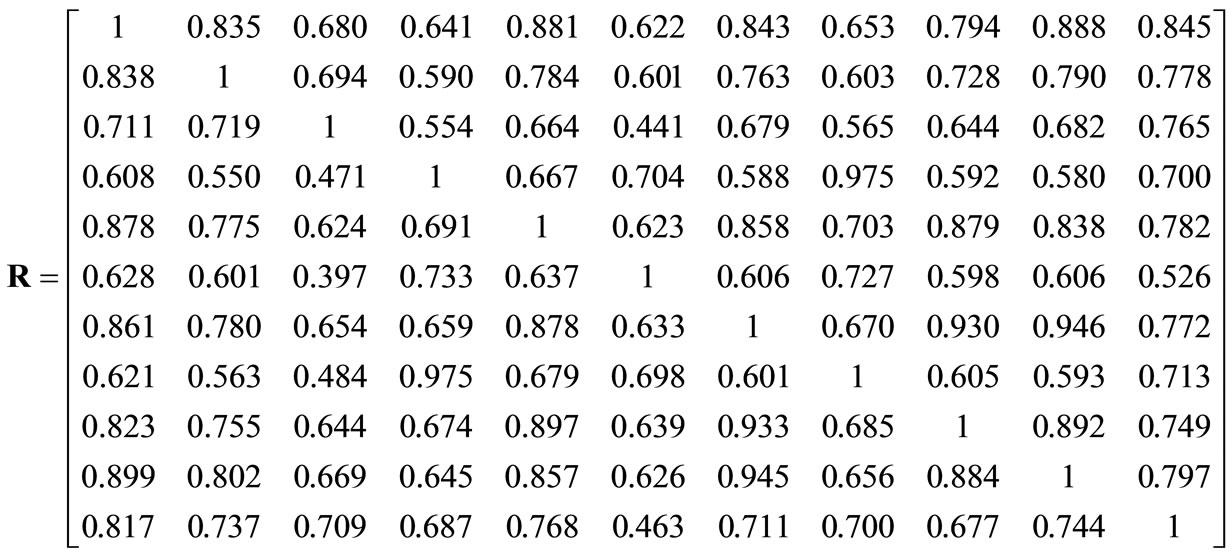
According to the expression (5), the coefficient matrix R is:
Eigenvalues of R are:
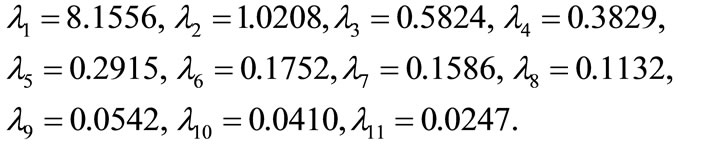

Table 1. Attributes of UUV.
And, 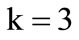 ,
, 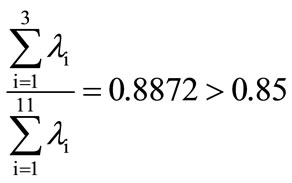 ,
,
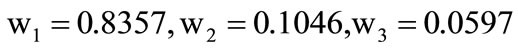

That is,
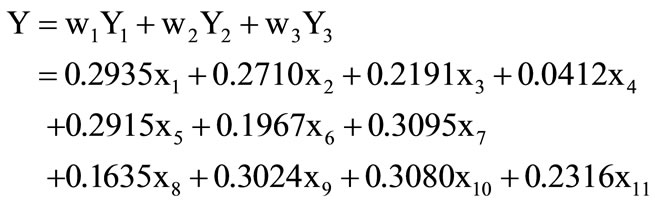
In the evaluation program, the standardization data should be taken as score of each variable. Then, the results of each scheme are,
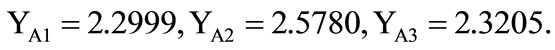
According to the evaluation results, the conclusion is that Scheme A2 is the best, Scheme A3 is better and Scheme A1 is the last. And the sequence is consistent with the evaluation result by classic PCA.
At the same time, in the eigenvector P2, coefficients of attributes x4, x6 and x8 are all less than zero. It means that the three attributes need to be improved, and it is true.
4. Conclusions
In this paper, a new method for evaluating complex system, especially in small sample case, is presented. The innovation points of the method include:
1) In small sample case, the relation coefficient is not accurate to the relationship between attribute. Relation coefficient is substituted for grey relative degree in PCA.
2) Standardization method of each attribute value is modified to aim at evaluating objective. In general, each attribute falls into cost type or benefit type.
3) According to analyzing a UUV schemes evaluation problem, the validity of the method is verified.
REFERENCES
- X. Bian, H. P. Tian and Y. J. Guo, “The Supplier Dynamic Evaluation Method with the Character of Stimulation,” Nankai Business Review, Vol. 7, No. 4, 2004, pp. 55-58.
- W. M. Hong and J. Liu, “A Survey on Supply Chain Performance Measurement,” Commercial Research, No. 8, 2006, pp. 17-21.
- M. Wise, “Adapting Multivariate Analysis for Monitoring and Modeling of Dynamic Systems,” Master Thesis, University of Washington, Washington DC, 1991.
- F. B. Jonathan and F. S. Stephen, “A Tradeoff Analysis for Rough Terrain Cargo Handlers Using the AHP: An Example of Group Decision Making,” IEEE Transactions on Engineering Management, Vol. 37, No. 3, 1990. pp. 222-228. doi:10.1109/17.104292
- K. Cengiz, C. Ufuk and U. Ziya, “Multi-Criteria Supplier Selection Using Fuzzy AHP,” Logistics Information Management, Vol. 16, No. 6, 2003, pp. 382-394. doi:10.1108/09576050310503367
- R. T. Umut, E. Arzum and A. Gőner, “Solving a Layout Design Problem by Analytic Hierarchy Process (AHP) and Data Envelopment Analysis (DEA) Approach,” Proceeding of SPIE: The International Society for Optical Engineering, Vol. 5262, Providence, 29 October 2004, pp. 232-239.

