Journal of Information Security
Vol.06 No.04(2015), Article ID:59938,6 pages
10.4236/jis.2015.64027
Enhanced Contrast of Reconstructed Image for Image Secret Sharing Scheme Using Mathematical Morphology
Yogesh K. Meghrajani, Himanshu S. Mazumdar
Department of Electronics & Communication, Faculty of Technology, Dharmsinh Desai University, Nadiad, India
Email: yogesh_engg2.ec@ddu.ac.in, hsmazumdar@ddu.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2015; accepted 22 September 2015; published 25 September 2015
ABSTRACT
Visual secret sharing (VSS) is one of the cryptographic techniques of Image secret sharing scheme (ISSS) that performs encoding of secret message image (text or picture) into noise like black and white images, which are called as shares. Shares are stacked together and secret message image is decoded using human visual system. One of the major drawbacks of this scheme is its poor contrast of the recovered image, which improves if computational device is available while decoding. In this paper, we propose to improve poor contrast of classical VSS schemes for text or alphanumeric secret messages and low entropy images. Initially, stacked image is binarized using dynamic threshold value. A mathematical morphological operation is applied on the stacked image to enhance contrast of the reconstructed image. Moreover, a method is proposed that allows the size of the structuring element to change according to the contrast and the size of a stacked image. We perform experiments for different types of VSS schemes, different share patterns, different share types (rectangle and circle), and low entropy images. Experimental results demonstrate the efficacy of the proposed scheme.
Keywords:
Contrast, Mathematical Morphological Operator, Image Secret Sharing, Visual Secret Sharing

1. Introduction
An image secret sharing scheme (ISSS) is a cryptographic technique to hide secret message image into meaningless images, which reveal no information about the secret message; called as shares. Typically, the secret message image contains text or picture where text is short alphanumeric message or password. Super- imposition of all shares reveals secret message. There are two major categories in ISSS: one is the visual secret sharing (VSS) scheme and the other is the polynomial-based ISSS (PISSS). VSS scheme is also known as visual cryptography scheme (VCS) [1] . Classical VSS reveals secret message without using any computational device and uses human visual system (HVS) only [1] - [8] . Typically, classical VSS schemes have recognizable recons- truction. Further, VSS schemes are also proposed for circular shares [6] [9] and cylinderical shares [13] . Contrarily, the PISSS can recover the secret image without any distortion, while it needs the computation [10] .
Another category of VSS scheme proposed with two decoding options, where the secret image is revealed both by stacking the shares and by computation. This scheme is called as Two-in-one image secret sharing scheme (TiOISSS) [10] [11] . TiOISSS can decode secret images for preview by HVS when computational device is temporarily unavailable. When the computational device is available during the decoding scene, a high quality image is obtained for high-end applications. Though above-mentioned schemes give two decoding options, they suffer from pixel expansion and their lossless reconstruction is specific to the share generation schemes. Additionally, Wu et al. [12] showed decryptions using OR and XOR which is another example of two options decoding. Here, OR is used for HVS and XOR is applied for computational system. Furthermore, Viet et al. [16] introduced additional operation, called reversing, which can be used by participants in the reconstruction phase to enhance contrast. However, their scheme has many drawbacks including pixel expansion.
In this paper, we propose a mathematical morphology based scheme to achieve almost ideal contrast of classical VSS schemes for text message image. Here, image after stacking at receiver is considered as an input. Otsu’s method is utilized to convert grayscale image into binary image. Further, image contrast enhances by mathematical morphological operation using appropriate size of square structuring element (SE). Notably, the proposed method computes size of SE from given input image itself.
Typically, for a given stacked text message image, impulse noise (pepper) is present. Briefly describing, few popular techniques to remove this impulse noise are isolated pixel removal technique, and adaptive median filter. Here, isolated pixel removal algorithm removes only isolated pixels, whereas probability of two or more pixels in a cluster is very high. Same way, adaptive median filter works well if the spatial density of the impulse noise is not very large. Hence, mathematical morphological opening operation is employed to remove impulse noise.
A possible application scenario of two options decoding as described in [12] , is as follows. When compu- tation resources are not available, stacking of shares decrypt the secret image though facing alignment issues. When computational device is available, contrast of the reconstructed image is enhanced up to almost ideal contrast by proposed method. Additionally, when computational resources are available during the decoding scene, a high quality image is obtained for high end applications [11] . It is noteworthy that the proposed scheme is independent of secret encoding and reconstruction, and works well for variety of image sharing schemes. The proposed scheme is like second step of TiOISSS [10] - [12] for VSS schemes for text secret message. Addi- tionally, our scheme can also employ to low entropy secret images.
The rest of this paper is organized as follows: Section 2 describes the proposed scheme. Section 3 shows experimental results and further discussion of the proposed scheme, and in Section 4, we conclude this paper.
2. Proposed Scheme
Analogous to second step of TiOISSS, stacked image is considered as an input image. Stacked grayscale image has mainly foreground message and noisy background. Primarily, image is required to be converted into binary using optimum threshold value. Though histograms of the different input images represent bi-modal behavior, resultant threshold values vary in wide range. Hence, Otsu’s method [17] evaluates optimum threshold value. Otsu’s method is employed to perform automatically clustering-based thresholding. Subsequently, a morpholo- gical opening operation is applied. In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:
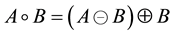 (1)
(1)
where  and
and 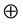 denote erosion and dilation, respectively.
denote erosion and dilation, respectively.
Set erosion and dilation are formulated based on structuring elements (SEs). SE is a small set or subimage, used to probe an image under study for properties of interest. Here, we employ standard symmetric square binary SE of value 1. However, optimum SE width (W) is required to select for generalized solutions, as higher W of SE eliminates message content whereas lower W of SE keeps noise elements. Therefore, probability of noise cluster is calculated for the optimum value of W. Here, input stacked result has typically white background (value 0) with pepper noise with black foreground message (value 1), whereas SE of width W eliminates W ´ W noise cluster. In stacked image, probability of black pixel is defined as,
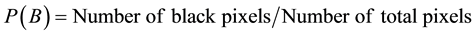 (2)
(2)
Whereas, probability of noise cluster of square W elements is,
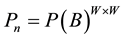 (3)
(3)
While, possibility of occurrence of such noise cluster in M ´ N size image is,
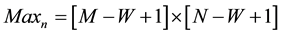 (4)
(4)
The probability of noise cluster in computed image reduces exponentially with increasing dimension of SE. This is explained as follows. Here, as image size increases,  increases which in turn, increases possibility of the noise cluster, whereas as W increases,
increases which in turn, increases possibility of the noise cluster, whereas as W increases,  decreases which in turn decreases the probability of noise cluster. Hence,
decreases which in turn decreases the probability of noise cluster. Hence,  and
and 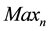 decide the W. Here, we consider high spatial resolution image, i.e. 1600 ´ 1200. For such high spatial resolution and typical lower value of W,
decide the W. Here, we consider high spatial resolution image, i.e. 1600 ´ 1200. For such high spatial resolution and typical lower value of W, 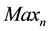 approximates to M ´ N times noise region. As a result,
approximates to M ´ N times noise region. As a result, 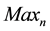 is
is , which is defined as number of trials. Hence,
, which is defined as number of trials. Hence, 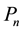 should be sufficiently small. Considering W = 9 and P(B) = 0.75 for VSS scheme,
should be sufficiently small. Considering W = 9 and P(B) = 0.75 for VSS scheme,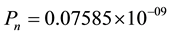 . This means, probability of occurrence of one noise cluster requires
. This means, probability of occurrence of one noise cluster requires 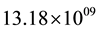 trials (1/Pn), which is very high compared to the
trials (1/Pn), which is very high compared to the
where k = number of attempts to generate noise cluster
Using Equation (3) and Equation (4),

If we solve Equation (5) for exact solution, we get 



Since P(B) is always < 1, denominator turns to positive value and as W is always positive integer, we do not consider the negative solution. Additionally, for float valued W, next odd value is selected. Here, small change in P(B) makes larger change in W, whereas numerator terms comparatively affects less. Logically, P(B), probability of black pixels, is related to contrast, so as it changes, W changes rapidly. Whereas for same P(B) value, size of image is not much effected comparatively. Practically, for highly noisy images, W has large values. Very large value of W erodes secret message. Hence, cut-off value of W is set to 9. This cut-off can be increased provided secret message width allows.
3. Experimental Results and Discussion
Experiments are conducted for different stacked messages [2] - [7] [12] [13] to demonstrate the feasibility of the proposed method. As a prerequisite step, we apply intensity thresholding using Otsu's algorithm followed by mathematical morphological opening operation. Table 1 shows the threshold value obtained from Otsu algorithm, SE size calculated using proposed algorithm, and SE size considered for experiments for different type and different size of images. In case the calculated SE size results into a float number, our algorithm takes next odd natural number as SE size.
Here, Figure 1(a), Figure 1(b), and Figure 1(d) show secret image, result of stacking two shares, and result of stacking three shares of (2, 3) VSS scheme [2] whereas Figure 1(c) and Figure 1(e) represent the result of proposed method applied on (b) and (d) respectively. One secret image and stacked image of (2, 2) VSS scheme for sharing multiple secrets [3] and result of our scheme are presented in Figure 2. Likewise, secret image, stacked images, and resultant images of our algorithm are exhibited for two patterns of (2, 2) VSS [4] in Figure 3. Further, Figure 4 demonstrates the results of (2, 2) and (3, 3) VSS using probabilistic method [5] . Additionally, outcome of (2, 2) VSS scheme using circular shares [6] for two secret images and VSS for cylindrical shares [13] are represented in Figure 5 and Figure 6 respectively.
Lastly, results showed for (2, 4) VSS using OR and XOR decryptions [12] where Figures 7(a)-(d) are secret image, result of stacking all four shares using OR, result of stacking all four share using XOR, and result of our method respectively. Experimental result for low entropy image [7] is presented in Figure 8, where (a), (b), and (c) show secret image, the stacked image, and the result for (b) using proposed scheme.
Results show that the proposed scheme works well for different types of VSS schemes, different share patterns, and different share types. Where Figure 1 highlights (2, 3), (3, 3) VSS schemes, Figure 4 shows effectiveness of the scheme for (2, 2) and (3, 3) VSS schemes. In [3] , due to sharing multiple secrets, contrast of stacked image is very poor (1/15) which is improved to almost ideal as shown in Figure 2. Similarly, Figure 3 represent efficacy of the method for different patterns. Besides rectangle shares, proposed scheme provides almost ideal reconstruction for circular shares as shown in Figure 5.
Table 1. Objective numerical parameters of Figure 1 to 8 for k = 1000.
Figure 1. Using Chen [2] (2, 3) VSS (a) Secret image; (b) result of stacking two shares of Chen’s (2, 3) VSS; (c) the result for (b) using our method; (d) result of stacking three shares of Chen’s (2, 3) VSS; (e) the result for (d) using our method.

Figure 2. Using Feng [3] (2, 2) VSS (a) secret image; (b) the result of stacking for one secret message [3] ; (c) the result for (b) using proposed method.

Figure 3. Using Yang [4] (2, 2) VSS (a) secret image; (b) the result of stacking for one pattern [4] ; (c) the result for (b) using our method; (d) the result of stacking for another pattern [4] ; (e) the result for (d) using our method.

Figure 4. Using Yang [5] ProbVSS scheme (a) secret image; (b) the result of stacking for Yang’s (2, 2) ProbVSS; (c) the re- sult for (b) using proposed method; (d) the result of stacking for Yang’s (3, 3) ProbVSS; (e) proposed method result for (d).

Figure 5. Using Shyu [6] multiple secret sharing in visual cryptography (a) secret image; (b) the result of stacking circle shares-


Figure 6. Using Salehi [13] VSS by cylindrical random grid (a) original secret image 1; (b) the result of stacking shares; (c) the result for (b) using proposed scheme.

Figure 7. Using Wu [12] VSS with OR and XOR decryptions (a) secret image; (b) the result of stacking using Wu’s OR decryption; (c) the result using Wu’s XOR decryption; (d) the result for (b) using proposed scheme.

Figure 8. Using Lin [7] flip visual cryptography (a) secret image; (b) the result of stacking using Lins block-based expanded version of scheme 1; (c) the result for (b) using proposed scheme.
Additionally, we compare proposed method with the Wu et al. [12] method when all four shares are stacked. Here, our method gives improved performance compared with Wu et al. [12] when computational device is employed. Finally, experimental results prove that our method works well for low entropy images also. However, mathematical morphological operation smooths the stacked image. Though our scheme assures improved contrast for classical VSS, size of SE plays a significant role. For a stacked image, secret message width should be higher than experimental SE size else secret message erodes in first step itself. Moreover, we have also verified the proposed scheme for results of other schemes [8] [14] [15] .
4. Conclusion
In this paper, we propose a generalized solution using mathematical morphological opening operation to remove noise clusters from the stacked message image of VSS. Stacked grayscale image is converted to binary image with distinct threshold value using Otsu’s algorithm. Mathematical morphological opening operation is applied on resultant image. Width of square SE is formulated from the stacked image with higher cut-off value of 9. Here, contrast of the stacked image plays significance role compared to size. Even small difference in contrast value makes large variation in SE size whereas for the similar contrast values, SE varies little. The removal of noise from the image improves the contrast and reconstructs received image from recognizable to almost ideal contrast. Here, secret message will be eroded if the width of the secret message is less than the experimental SE. The proposed method works well for the application scenario of two options decoding techniques. Additionally, proposed scheme can be implemented for handheld devices like mobile phone.
Cite this paper
Yogesh K.Meghrajani,Himanshu S.Mazumdar, (2015) Enhanced Contrast of Reconstructed Image for Image Secret Sharing Scheme Using Mathematical Morphology. Journal of Information Security,06,273-279. doi: 10.4236/jis.2015.64027
References
- 1. Naor, M. and Shamir, A. (1995) Visual Cryptography. In: Proceedings of the Advances in Cryptology— EUROCRYPT’94, Lecture Notes in Computer Science (Volume 950), 1-12. http://dx.doi.org/10.1007/bfb0053419
- 2. Chen, S.-K. and Lin, S.-J. (2012) Optimal (2,n) and (2, Infinity) Visual Secret Sharing by Generalized Random Grids. Journal of Visual Communication and Image Representation, 23, 677-684. http://dx.doi.org/10.1016/j.jvcir.2012.03.004
- 3. Feng, J.-B., Wu, H.-C., Tsai, C.-S., Chang, Y.-F. and Chu, Y.-P. (2008) Visual Secret Sharing for Multiple Secrets. Pattern Recognition, 41, 3572-3581. http://dx.doi.org/10.1016/j.patcog.2008.05.031
- 4. Yang, C.-N. and Chen, T.-S. (2005) Aspect Ratio Invariant Visual Secret Sharing Schemes with Minimum Pixel Expansion. Pattern Recognition Letters, 26, 193-206. http://dx.doi.org/10.1016/j.patrec.2004.08.025
- 5. Yang, C.N. (2004) New Visual Secret Sharing Schemes Using Probabilistic Method. Pattern Recognition Letters, 25, 481-494. http://dx.doi.org/10.1016/j.patrec.2003.12.011
- 6. Shyu, S.J., Huang, S.Y., Lee, Y.K., Wang, R.Z. and Chen, K. (2007) Sharing Multiple Secrets in Visual Cryptography. Pattern Recognition, 40, 3633-3651. http://dx.doi.org/10.1016/j.patcog.2007.03.012
- 7. Lin, S.-J., Chen, S.-K. and Lin, J.-C. (2010) Flip Visual Cryptography (FVC) with Perfect Security, Conditionally-Optimal Contrast, and No Expansion. Journal of Visual Communication and Image Representation, 21, 900-916. http://dx.doi.org/10.1016/j.jvcir.2010.08.006
- 8. Hou, Y.C. and Quan, Z.Y. (2011) Progressive Visual Cryptography with Unexpanded Shares. IEEE Transactions on Circuits and Systems for Video Technology, 21, 1760-1764. http://dx.doi.org/10.1109/TCSVT.2011.2106291
- 9. Wu, H.-C. and Chang, C.-C. (2005) Sharing Visual Multi-Secrets Using Circle Shares. Computer Standards & Interfaces, 28, 123-135. http://dx.doi.org/10.1016/j.csi.2004.12.006
- 10. Lin, S.-J. and Lin, J.-C. (2007) VCPSS: A Two-in-One Two-Decoding-Options Image Sharing Method Combining Visual Cryptography (VC) and Polynomial-Style Sharing (PSS) Approaches. Pattern Recognition, 40, 3652-3666. http://dx.doi.org/10.1016/j.patcog.2007.04.001
- 11. Yang, C.-N. and Ciou, C.-B. (2010) Image Secret Sharing Method with Two-Decoding-Options: Lossless Recovery and Previewing Capability. Image and Vision Computing, 28, 1600-1610. http://dx.doi.org/10.1016/j.imavis.2010.04.003
- 12. Wu, X. and Sun, W. (2013) Random Grid-Based Visual Secret Sharing with Abilities of OR and XOR Decryptions. Journal of Visual Communication and Image Representation, 24, 48-62. http://dx.doi.org/10.1016/j.jvcir.2012.11.001
- 13. Salehi, S. and Balafar, M.A. (2014) Visual Multi Secret Sharing by Cylindrical Random Grid. Journal of Information Security and Applications, 19, 245-255. http://dx.doi.org/10.1016/j.jisa.2014.05.003
- 14. Wu, X. and Sun, W. (2012) Random Grid-Based Visual Secret Sharing for General Access Structures with Cheat-Preventing Ability. Journal of Systems and Software, 85, 1119-1134. http://dx.doi.org/10.1016/j.jss.2011.12.041
- 15. Lee, K.H. and Chiu, P.L. (2011) A High Contrast and Capacity Efficient Visual Cryptography Scheme for the Encryption of Multiple Secret Images. Optics Communications, 254, 2730-2741. http://dx.doi.org/10.1016/j.optcom.2011.01.077
- 16. Viet, D.Q. and Kurosawa, K. (2004) Almost Ideal Contrast Visual Cryptography with Reversing. In: Proceedings of Topics in Cryptology—CT-RSA 2004, Lecture Notes in Computer Science (Volume 2964), 353-365. http://dx.doi.org/10.1007/978-3-540-24660-2_27
- 17. Otsu, N. (1979) A Threshold Selection Method from Gray-Level Histogram. IEEE Transactions on System Man Cybernetics, 9, 62-66. http://dx.doi.org/10.1109/TSMC.1979.4310076








