Materials Sciences and Applications
Vol.08 No.03(2017), Article ID:74613,13 pages
10.4236/msa.2017.83016
The Barrier Properties of Flake-Filled Composites with Precise Control of Flake Orientation
A. Tsiantis, T. D. Papathanasiou*
Department of Mechanical Engineering, University of Thessaly, Volos, Greece

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 7, 2017; Accepted: March 6, 2017; Published: March 9, 2017
ABSTRACT
Additive manufacturing, especially in the form of 3D printing, offers the exciting possibility of generating heterogeneous articles with precisely controlled internal microstructure. One area in which this feature can be of significant advantage is in diffusion control, specifically in the design and fabrication of microstructures which optimize the rate of transport of a solute to and from a contained fluid. In this work we focus on the use of flakes as diffusion-control agents and study computationally and theoretically the effect of orientation on the barrier properties of flake-filled composites. We conducted over 1500 simulations in two-dimensional, doubly-periodic unit cells each containing up to 3000 individual flake cross-sections which are randomly placed and with their axes forming an angle (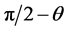 ) with the direction of macroscopic diffusion. We consider long-flake systems of aspect ratio (
) with the direction of macroscopic diffusion. We consider long-flake systems of aspect ratio (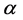 ) 100 and 1000, from the dilute (
) 100 and 1000, from the dilute (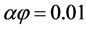 ) and into the concentrated (
) and into the concentrated (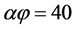 ) regime. Based on the rotation properties of the diffusivity tensor, we derive a model which is capable of accurately reproducing all computational results (
) regime. Based on the rotation properties of the diffusivity tensor, we derive a model which is capable of accurately reproducing all computational results (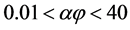 and
and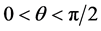 ). The model requires as inputs the two principal diffusivities of the composite, normal and parallel to the flake axis. In this respect, we find the models of Lape et al. [1] and Nielsen [2] form an excellent combination. Both our model and our computational data predict that at
). The model requires as inputs the two principal diffusivities of the composite, normal and parallel to the flake axis. In this respect, we find the models of Lape et al. [1] and Nielsen [2] form an excellent combination. Both our model and our computational data predict that at 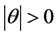 the quadratic dependence of the Barrier Improvement Factor (BIF) on (
the quadratic dependence of the Barrier Improvement Factor (BIF) on (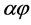 ) is lost, with the BIF approaching a plateau at higher values of (
) is lost, with the BIF approaching a plateau at higher values of (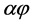 ). This plateau is lower as (
). This plateau is lower as (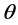 ) increases. We derive analytical estimates of this maximum achievable BIF at each level of misalignment; these are also shown to be in excellent agreement with the computational results. Finally we show that our computational results and model are in agreement with experimental evidence at small values of (
) increases. We derive analytical estimates of this maximum achievable BIF at each level of misalignment; these are also shown to be in excellent agreement with the computational results. Finally we show that our computational results and model are in agreement with experimental evidence at small values of (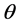 ).
).
Keywords:
Barrier Properties, Composite Films, Diffusion, Flakes, Platelets, 3D Printing

1. Introduction
Additive manufacturing, especially in the form of 3D printing, offers the exciting possibility of generating articles with precisely controlled internal microstructure. One area in which this feature can be of significant advantage is in diffusion control, specifically in the design and fabrication of microstructures which allow for minimization of the transport of a solute to/from a contained fluid. Flake-filled polymeric composites, incorporating mica, glass or metallic flakes have found many uses in this direction, as they offer significant processing and property advantages, namely high dimensional stability and low warpage in molding, uniform in-plane mechanical properties, corrosion protection, sound insulation as well as appearance and color control [3] [4] [5] [6] [7] . Micron-sized flakes of inorganic materials such as mica, nano-scale platelets of clay minerals such as hectrite, saponite and montmorillonite and more recently graphene-oxide platelets of aspect ratios well over 1000, have been used for this purpose [8] . It has been demonstrated that incorporation of such fillers aligned perpendicular to the direction of macroscopic diffusion can be very effective in increasing the tortuosity of the diffusion path of the diffusing species. When the flakes are randomly placed, as would be the case in a flake composite manufactured from the melt, the predicted improvement in barrier efficiency ranges from being ~(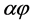 ) in dilute systems, where (
) in dilute systems, where (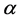 ) is the aspect ratio and (
) is the aspect ratio and (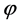 ) the volume fraction of the flakes, to being ~
) the volume fraction of the flakes, to being ~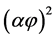 in more concentrated dispersions [1] [9] - [16] .
in more concentrated dispersions [1] [9] - [16] .
One notable disadvantage of traditional processing methods vis-à-vis flake- filled composites is the fact that flake orientation cannot be precisely controlled. In such operations (extrusion, compression or injection molding, thermoforming and others) flake orientation is achieved due to the propensity of the flakes to orient in accordance to the prevailing flow field―either in the main direction of flow when the flow is shear or transverse to it when the flow is extensional [17] . An additional shortcoming of traditional flow-processing routes is the inability to utilize high flake loadings since, in that case, the viscosity of the resulting melt becomes prohibitively high. Given the capability afforded by 3D printing to fully control flake orientation as well as generate articles with flake loadings approaching those at maximum packing, it is desirable to predict the effective diffusion coefficient (or its inverse, the barrier improvement factor, BIF) as an explicit function of the flake orientation angle and for very high, previously untenable, concentrations.
The two main approaches which have been used in the literature to-date for this purpose are (i) an ad-hoc incorporation of orientation metrics in existing models for the BIF [8] [18] and (ii) derivation of BIF models from diffusion path calculations [19] [20] [21] . In both cases, the proposed models have been derived for low or very-low flake concentrations and have not been extensively tested in the moderate to high-concentration regime, which will be of importance in any 3D printing application. In addition, by not respecting the rotational properties of the diffusivity tensor, these models are not grounded on a sound theoretical footing. This paper addresses the above issues both computationally and theoretically, by proposing a model based on the two principal diffusivities of a flake composite. We also show that the implications of our theoretical model are fully supported by extensive computational results.
2. Computational
We carry out steady-state diffusion computations in doubly-periodic unit cells containing up to 3000 individual flake cross-sections. These are added in the domain sequentially, using a Random Sequential Addition (RSA) procedure. Specifically, at each flake placement attempt, two random numbers are used to assign the coordinates of the flake center while its orientation angle (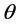 ) is fixed and the same for all flakes. If, after placement, no overlap with other flakes is detected, the process continues with the next flake, until the desired number of flakes has been placed, or, until no flake can be placed after 50,000 attempts; in this case no geometry is generated. In order to enable subsequent meshing of the computational domain, a minimum allowable distance between flakes is imposed; this is (
) is fixed and the same for all flakes. If, after placement, no overlap with other flakes is detected, the process continues with the next flake, until the desired number of flakes has been placed, or, until no flake can be placed after 50,000 attempts; in this case no geometry is generated. In order to enable subsequent meshing of the computational domain, a minimum allowable distance between flakes is imposed; this is (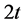 ) where (
) where (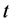 ) is the thickness of the flake. Since in this work we have dealt with flakes of high aspect ratio (
) is the thickness of the flake. Since in this work we have dealt with flakes of high aspect ratio (







In multi-particle simulations, use of doubly-periodic cells is essential when dealing with elongated particles so as to eliminate artifacts of oriented (or, depleted) layers which would otherwise appear adjacent to cell boundaries [11] [16] . The effect of the RVE dimensions on the computed effective diffusivity is also eliminated when using periodic unit cells. A sample unit cell, showing flakes oriented at an angle θ = 0.8 rad with respect to the horizontal (x) axis (extended slightly outside the limits of the unit cell to show the doubly-periodic geometry) is shown in Figure 1.
The boundary conditions are cyclic on the right and left boundaries, namely



Figure 1. Sample unit cell―doubly-periodic―containing 500 flake crossections, all oriented at an angle θ = 0.8 rad to the horizontal (x) axis.

placed flakes. The computational meshes are created by the mesh generating program Salome through an in-house automated procedure and contain ~106 triangular elements.
These meshes are then used by Open Foam to solve the steady-state diffusion equation

where the subscript (n) indicates numerically computed value, n is the outward unit vector and (L) is the width of the unit cell. Because of impermeable flakes crossing boundaries, which results in sudden local changes of the flux, care must be taken in performing this integration. In this work, we used adaptive intervals and only accepted values of the integral when these were convergent with refinement. Equating this flux with the one obtained from Fick’s law in a macroscopic equivalent cell (whose diffusivity is Deff) we obtain
where 



3. Results and Discussion
In the following we present the results of a comprehensive computational study of diffusion across doubly-periodic unit cells, each containing up to N = 3000 randomly placed impermeable flakes of rectangular cross-section. In such a system, the orientation of each flake is defined by the orientation angle (θ) formed between the vertical axis (y), which is taken to be the direction of macroscopic diffusion, and the outward normal vector on the flake surface. The horizontal axis is indicated as (







3.1. Effect of Flake Misalignment on Effective Diffusivity
Representative results of the distribution of (C), also showing the corresponding flake distributions, are shown in Figure 2 and Figure 3.
We define as D11 the diffusivity of such a system when q = 0˚ (all flakes oriented perpendicular to the direction of macroscopic diffusion) and D22 the diffusivity when q = 90˚ (all flakes oriented parallel to the direction of diffusion). D11 and D22 are the principal values of the two-dimensional diffusivity tensor, D. The diffusivity tensor 






Hence

Therefore, the effective diffusivity of this system in the direction (y) forming
Figure 2. Distribution of concentration in geometries with θ = 0 and
Figure 3. Distribution of concentration in geometries with 

an angle (

We will investigate the use of Equation (2) to determine
In the first instance we have compared the computational results for dilute cases (

Nielsen’s [2] , model has been used for D11 and D22, namely 

Extensive comparisons have shown that predictions of Equation (2) based on Nielsen’s model for D11 and D22 are close to the computational results only for the very dilute regime (

It is of course possible to use diffusivity models for D11 and D22 more suitable for concentrated suspensions. A review and evaluation of available models has been carried out by Chen and Papathanasiou [11] . Of the models discussed there, we single out those of Cussler and co-workers [1] [9] mainly because of their relevance to the systems modeled here (randomly placed flakes) as well as due to the small number of adjustable parameters needed in their implementation and their extensive use in the literature. Lape et al. [1] proposed that for diffusion across arrays of unidirectional randomly placed flakes it is
In deriving this model, the tortuosity factor was taken to be 1 + αφ/3 and it was further assumed that the ratio of the areas available for diffusion is
Implicit in the above derivation is the assumption that the diffusion paths around a flake form straight lines; therefore it is not unreasonable to treat the factor “3” in the expression above as a geometrical parameter that may be adjusted if so suggested by the data. Since that was found to be the case in analyzing our data, we use the model of Lape et al. [1] in the form:

in which (

where (
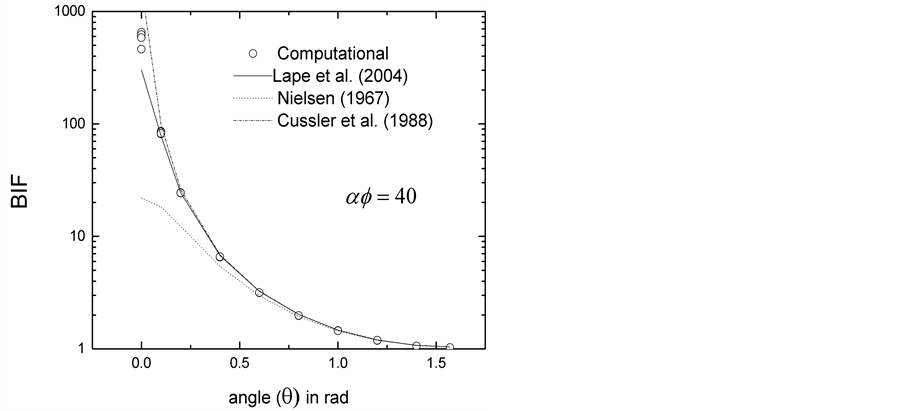
Figure 4. Comparison of computational results (points) with predictions of Equation (2) for 




comparison between the computational results, for flakes with 

















Additional comparisons for 



In summary, our computational results and the comparisons presented above have shown that the effective diffusivity Deff of a system of randomly placed flakes oriented at an angle (

Figure 5. Comparison of computational results (points) with predictions of Equation (2) for 


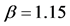

where

in which 

From Equation (2) it can be seen that the BIF implied by our model, (setting, without loss of generality or relevance, D22~D0~1) is

As shown in Figure 6, at each value of (





3.2. The Effect of Flake Concentration
In aligned systems, it is known [1] [9] [10] that the BIF scales with 




Figure 6. Predictions of Equation (7) (broken lines) showing its asymptotic approach to the experimental result represented by Equation (6) (solid line). Larger values of D11 correspond to more dilute systems.
Figure 7. Summary of computational results (circles) for 




plateau value; this plateau is lower the larger the misalignment angle (θ) is. The implication of this result is that for the full potential of large-
3.3. Limiting Behavior of the BIF at Very High (αφ).
In light of the excellent agreement between computational results and Equation (5) it is possible to use the latter to obtain analytical estimates of the leveling-off values of the BIF at each (θ), by observing that the first term of Equation (5) becomes negligible at high (

Figure 8 compares our computational results to the predictions of Equation (8) as well as the approach to that limit based on Equation (5). A conclusion is obvious―the quadratic rise of the BIF with (





The above comments and results are particularly pertinent to high aspect ratio
Figure 8. The approach to the BIF limit (as predicted by Equation (8), dotted lines) for θ = 0.1, 0.2 and 0.4 (in rad) as well as the predictions of Equation (5) (solid lines). Points are computational results. α = 1000.
Figure 9. Computed BIF at 
flakes, such as found in exfoliated nanoclay or graphene composites, for which even at low (





4. Conclusion
In this study we proposed a model for the Barrier Improvement Factor (BIF) of misaligned flake composites which is valid up to very high flake concentrations, as could be found in composites fabricated by 3D printing. The model requires as inputs the two principal diffusivities of the composite, normal and parallel to the flake axis. In this respect, we find that the models of Lape et al. [1] and Nielsen [2] form an excellent combination. The simple algebraic form of the proposed model makes it usable without recourse to special computing facilities. This model was tested exhaustively by comparing to predictions of 2D computer simulations which included up to 3000 randomly placed but uniformly oriented flake cross-sections in each RVE. Each cross-section forms an angle (





Cite this paper
Tsiantis, A. and Papathanasiou, T.D. (2017) The Barrier Properties of Flake-Filled Composites with Precise Control of Flake Orientation. Materials Sciences and Applications, 8, 234-246. https://doi.org/10.4236/msa.2017.83016
References
- 1. Panwar, A., Choudhary, V. and Sharma, D.K. (2013) Role of Compatibilizer and Processing Method on the Mechanical, Thermal and Barrier Properties of PS/ Organoclay Nanocomposites. Journal of Reinforced Plastics and Composites, 32, 998-1002.
https://doi.org/10.1177/0731684413477770 - 2. Pavlidou, S. and Papaspyrides, C.D. (2008) A Review on Polymer-Layered Silicate Nano-Composites. Progress in Polymer Science, 33, 1119-1198.
https://doi.org/10.1016/j.progpolymsci.2008.07.008 - 3. Pajarito, B. and Kubuchi, M. (2013) Flake-Filled Polymers for Corrosion Protection. Journal of Chemical Engineering of Japan, 46, 18-26.
https://doi.org/10.1252/jcej.12we133 - 4. Mohamadi, M., Garmabi, H. and Keshavarzi, F. (2016) An Investigation on the Effects of Organo-Modified Fluoromica on Mechanical and Barrier Properties of Compatibilized HDPE Nanocomposite Films. Journal of Plastic Film and Sheeting, 32, 10-33.
https://doi.org/10.1177/8756087915569097 - 5. Lagaron, J.M. and Nunez, E. (2011) Nanocomposites of Moisture-Sensitive Polymers and Biopolymers with Enhanced Performance for Flexible Packaging Applications. Journal of Plastic Film and Sheeting, 28, 79-89.
https://doi.org/10.1177/8756087911427756 - 6. Lee, K.-H., Hong, J., Kwak, S.J., Park, M. and Son, J.G. (2015) Spin Self-Assembly of Highly Ordered Multilayers of Graphene-Oxide Sheets for Improving Oxygen Barrier Performance in Polyolefins. Carbon, 83, 40-47.
https://doi.org/10.1016/j.carbon.2014.11.025 - 7. Cussler, E.L., Hughes, S.E., Ward, W.J. and Aris, R. (1988) Barrier Membranes. Journal of Membrane Science, 38, 161-74.
https://doi.org/10.1016/S0376-7388(00)80877-7 - 8. Lape, N.K., Nuxoll, E.E. and Cussler, E.L. (2004) Polydisperse Flakes in Barrier Films. Journal of Membrane Science, 236, 29-37.
https://doi.org/10.1016/j.memsci.2003.12.026 - 9. Lebovka, N., Khrapatiy, S., Vygornitskyi. and Pivovarova, N. (2014) Barrier Properties of K-Mer Packings. Physica A, 408, 19-27.
https://doi.org/10.1016/j.physa.2014.04.019 - 10. Chen, X. and Papathanasiou, T.D. (2007) Barrier Properties of Flake-Filled Membranes: Review and Numerical Evaluation. Journal of Plastic Film and Sheeting, 23, 319-346.
https://doi.org/10.1177/8756087907088437 - 11. Dondero, M., Cisilino, A.P. and Tomba, J.P. (2013) Experimental Validation of Computational Models for Mass Transport through Micro Heterogeneous Membranes. Journal of Membrane Science, 437, 25-32.
https://doi.org/10.1016/j.memsci.2013.02.039 - 12. Minelli, M., Baschetti, M.G. and Doghierri, F. (2011) A Comprehensive Model for Mass Transport Properties in Nanocomposites. Journal of Membrane Science, 381, 10-20.
https://doi.org/10.1016/j.memsci.2011.06.036 - 13. Tan, B. and Thomas, N.L. (2016) A Review of the Water Barrier Properties of Polymer/Clay and Polymer/Grapheme Nanocomposites. Journal of Membrane Science, 514, 595-612.
https://doi.org/10.1016/j.memsci.2016.05.026 - 14. DeRocher, J.P., Gettelfinger, B.T., Wang, J., Nuxoll, E.E. and Cussler, E.L. (2005) Barrier Membranes with Different Sizes of Aligned Flakes. Journal of Membrane Science, 254, 21-30.
https://doi.org/10.1016/j.memsci.2004.12.025 - 15. Papathanasiou, T.D. and Tsiantis, A. (2016) Orientational Randomness and Its Influence on the Barrier Properties of Flake-Filled Composite Films. Journal of Plastic Film and Sheeting, On Line.
- 16. Papathanasiou, T.D. and Guell, D.C. (1997) Flow Induced Alignment in Composite Materials. Woodhead Publishing, Cambridge.
https://doi.org/10.1201/9781439822739 - 17. Bharadwaj, R.K. (2001) Modeling the Barrier Properties of Polymer-Layered Silicate Nanocomposites. Macromolecules, 34, 9189-9192.
https://doi.org/10.1021/ma010780b - 18. Greco, A. (2014) Simulation and Modeling of Diffusion in Oriented Lamellar Nanocomposites. Computational Materials Science, 83, 164-170.
https://doi.org/10.1016/j.commatsci.2013.11.019 - 19. Greco, A. and Maffezzoli, A. (2013) Two-Dimensional and Three-Dimensional Simulation of Diffusion in Nanocomposite with Arbitrarily Oriented Lamellae. Journal of Membrane Science, 442, 238-244.
https://doi.org/10.1016/j.memsci.2013.04.038 - 20. Sorrentino, A., Tortora, M. and Vittoria, V. (2006) Diffusion Behavior in Polymer-Clay Nanocomposites. Journal of Polymer Science Part B: Polymer Physics, 44, 265-274.
https://doi.org/10.1002/polb.20684 - 21. Nielsen, L.E. (1967) Models for the Permeability of Filled Polymer Systems. Journal of Macromolecular Science Part A: Chemistry, 5, 929-942.
https://doi.org/10.1080/10601326708053745 - 22. Yang, C., Smyrl, W.H. and Cussler, E.L. (2004) Flake Alignment in Composite Coatings. Journal of Membrane Science, 231, 1-12.
https://doi.org/10.1016/j.memsci.2003.09.022 - 23. Eitzman, D.M., Melkote, R.R. and Cussler, E.L. (1996) Barrier Membranes with Tipped Impermeable Flakes. AIChE Journal, 42, 2-9.
https://doi.org/10.1002/aic.690420103