Materials Sciences and Applications
Vol.07 No.03(2016), Article ID:64787,9 pages
10.4236/msa.2016.73015
The Influence of Organo-Clay Ratio in the HIPS-OMMT Nanocomposites Analyzed by Proton Spin-Lattice and Spin-Spin Relaxation Times
Paulo Sérgio Rangel Cruz da Silva, Lívia Rodrigues Menezes, Maria Inês Bruno Tavares
Institute of Macromolecules Professor Eloisa Mano, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 January 2016; accepted 18 March 2016; published 21 March 2016
ABSTRACT
Spin-lattice and spin-spin relaxation times are one of the most attractive tools in the solid-state nuclear magnetic resonance spectroscopy to evaluate the level of clay dispersion in the nanocomposite matrices. The efficiency of the relaxation processes can be used to evaluate the nanoparticles intermolecular interactions and, consequently, the dispersion of them in the polymer matrix, the molecular dynamic of the hybrid compounds, as well as the molecular domains formation in an organic material. The determination of relaxation parameters was carried out to evaluate the organoclay exfoliation and intercalation process in the polymeric matrix, in addition to their dispersion and distribution in the matrix. The proton NMR relaxation data showed that the polymeric nanomaterials investigated presented good intermolecular interaction that promoted good nanoparticles dispersion and distribution in the hybrid materials. The proportion of 2% clay promoted a greater heterogeneity in the matrix compared to other ratios; 1% clay influenced only to the higher molecular rigidity phase; and 3% clay had a decrease in heterogeneity compared to 2% though still influenced the matrix as a whole. These results prove the efficiency of NMR technique in the evaluation of nanofillers interaction with polymer matrices, as well as their dispersion and distribution.
Keywords:
Polymeric Nanocomposites, Nanoparticles, Relaxation Times, NMR

1. Introduction
Solid-state nuclear magnetic resonance spectroscopy (NMR) provides powerful techniques for measurement of nuclear relaxation times, such as: spin-lattice relaxation time in the laboratory frame; spin-lattice relaxation time in the rotating frame, and spin-spin relaxation time in the laboratory frame. They differ in the following aspects: the first one promotes evaluation of the samples in the MHz scale; the second one is sensitive to the movements in the tens of kilohertz [1] - [5] ; and the third one comes from the loss of phase coherence among nuclei in the xy plane, which affects the relaxation of the component perpendicular to B0. The spin-lattice relaxation parameters involve changes in thermal equilibrium of spin systems and the responses of them are intrinsically related to the system’s molecular dynamic that is derived from the morphology of the systems [6] . Because of this broad coverage, the relaxation parameters are of great value to understand the dispersion of the nanoparticles in the polymer matrix, the interaction between nanocomposite components, the molecular dynamic of the hybrid compound, and the molecular domains formation in an organic material [7] . Therefore, these techniques are increasingly used to analyze the molecular dynamics of polymer systems, particularly polymeric nanocomposites [7] - [9] .
a) Spin-lattice relaxation time in the laboratory frame measurements
This parameter is also known as longitudinal relaxation and possesses a time constant T1; this is measured by the inversion-recovery pulse sequence (expression 1) [10] and the mechanism of this relaxation process occurs in the z-direction.
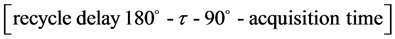 expression 1
expression 1
T1 relaxation corresponds to the process of establishing z component of the nuclear spin magnetization to its thermal equilibrium, and has a relaxation rate R1. The T1 values were determined by the Equation (1) [10] .
 . (1)
. (1)
T1 relaxation of spin 1/2 nuclei occurs in the absence of external influences. T1 relaxation is attributed to magnetic field fluctuations in the x, y direction. Such fluctuations are most effective when they occur at the Larmor precession frequency (νo). T1 relaxation is magnetic field dependent, since no varies with the magnetic field. The T1 parameter is sensitive to paramagnetic effect, thus the presence of paramagnetic metals (i.e. iron) influences the behavior of T1 values, making them decrease when the nuclei are near to this kind of metals.
b) Spin-lattice relaxation in the rotating frame measurements
The spin-lattice relaxation in the rotating frame (T1ρ) can be measured by the decay of the resolved carbons, during the variable contact time experiment (VCT) (Equation (2)) [4] , as a function of contact-time increment or under spin-lock conditions, which generates a rotating magnetic field near the resonant frequency perpendicular to the static magnetic field and, in this case, is observed in a small range of frequency compared to T1.
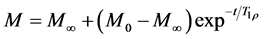 . (2)
. (2)
The variable contact time experiment allows determination of the T1ρ values for each resolved carbon, the efficiency in observing this relaxation time in the VCT experiment depends on the polarization transfer from the hydrogen nucleus to the carbon nucleus [4] [5] [11] . Therefore, one specific carbon, involved in the interaction process, can be selected to display the behavior of the molecular motions in the systems. As the T1ρ value is measured simultaneously with the NMR spectra during the relaxation of spin frequency after the pulse sequence, this parameter is not much influenced by paramagnetic metals. The mechanism to obtain the T1ρ values covers a limited range of molecular motion [4] : as much more is rigid the material, the value T1ρ is smaller. Furthermore, the measurement of this parameter is strongly dependent on the spatial proximity of the nanomaterial components due to spin diffusion of them. If the samples components are intimately mixed in the nanometer scale, they will have only one value of T1ρH [12] [13] .
c) Spin-spin relaxation time measurements
T2 represents loss of phase coherence among nuclei. T2 is normally smaller than T1 when we are analyzing solid samples, considering R = relaxation rate, R2 = 1/T2, R2 ³ R1; consequently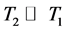 , due to the fact that the return of magnetization to the z-direction inherently causes loss of magnetization in the x-y plane (Equation (3)) [10] [14] [15] .
, due to the fact that the return of magnetization to the z-direction inherently causes loss of magnetization in the x-y plane (Equation (3)) [10] [14] [15] .
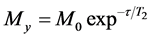 . (3)
. (3)
T2 relaxation is caused by fluctuations in any direction (xy plane) and the principal source of fluctuating magnetic fields in most molecules is molecular motion. There are several mechanisms by which molecular motions can influence nuclear relaxation processes: direct interactions with nearby magnetic nuclei (DD) and chemical shift effects (CSA), among others. Thus, according to the spin-spin relaxation mechanism this parameter is less influenced by paramagnetic metals.
These relaxation parameters have been used to analyze the molecular dynamic behavior in solids, such as polymers, and other kind of materials, and can be envisioned as good tools for the evaluation of polymer nanocomposites, as well.
In the present work, NMR relaxometry was used to evaluate the different nanostructured materials based on high impact polystyrene and organic modified montmorillonite with the objective of obtaining responses about the intermolecular interactions, as a consequence the dispersion and distribution of the nanoparticles in the polymer matrix. Particularly, proton spin-lattice and spin-spin relaxation times were measured using low-field nuclear magnetic resonance. The T1ρH was extracted from the series of 13C CPMAS decay intensities of C-1 carbon.
2. Experimental
2.1. Materials
Commercial organically modified montmorillonite (OMMT) was acquired from Bentec (Viscogel S7), which is modified with dimethyl benzyl hydrogenated. Commercial high-impact polystyrene in solid pallet form was purchased from Innova S.A. Chloroform and toluene were used as solvent pair, and they were received from Tedia Brazil.
2.2. Nanocomposites Preparation
The polymer was solubilized in a 250-mL Erlenmeyer flask with 50 mL of chloroform and 100 mL of toluene using mechanic stirring. The clay mass was added to the polymer mass at a concentration of 5%. The desired amount (1, 2 and 3% w/w) of OMMT was weighed and dispersed in 50 mL of chloroform using mechanic stirring. The polymer solution was stirred for 24 h. After obtaining a homogeneous mixture, the clay dispersion was stirred for 24 h, poured in the polymer solution and the resulting dispersion was stirred for another 24 h. After that period, the final dispersion was placed in a petri dish (150 mm diameter). The petri dishes were then placed in an oven at ~40˚C for 24 h to remove the solvents and allow the formation of the films. HIPS films were also obtained as described above without adding the OMMT in order to compare the characteristics of the different materials obtained [16] .
2.3. NMR Relaxation Measurements
The relaxation time was analyzed in a MARAN Ultra low-field NMR (LF-NMR) spectrometer (Oxford Instruments, Oxford, UK), using an 18 mm NMR tube, operating at 23 MHz for the hydrogen nucleus. The pulse sequence to obtain the spin lattice relaxation time data was inversion-recovery (recycle delay - 180˚ - τ - 90˚ - acquisition data) and the 90˚ pulse of 4.5 μs was calibrated automatically by the instrument’s software. The amplitude of the FID was sampled for twenty τ data points, ranging from 0.01 to 10,000 ms, using 40 data points and 4 scans for each point. The pulse sequence used to measure the spin-spin relaxation time was Carr-Purcell- Meiboom-Gil (CPMG) and the 90˚ pulse of 4.5 μs was calibrated automatically by the instrument’s software, and τ was 100 μs. The samples were analyzed at 27˚C. The relaxation values and relative intensities were obtained by fitting the exponential data with the aid of the WINFIT program. Distribution exponential fittings were performed using the WINDXP software, as a plot of relaxation amplitude versus relaxation time. Both WINFIT and WINDXP are commercial programs and come with the low-field NMR spectrometer.
All solid-state NMR spectra were obtained with a 7.4 Tesla spectrometer, operating at 75.4 MHz for 13C nuclei. The samples were packed in a 4 mm zirconia rotor that was spun in the magic angle at about 8 KHz for the 13C nuclei. The 13C cross polarization magic angle spinning (CPMAS) were first done to obtain the conditions to apply the variable contact time experiment (VCT), which were carried out using 3 seconds of recycle delay with the increase of contact-times varying from 100 to 8000 μs, the hydrogen decoupling field strength was 50 KHz. From this experiment it was also determined the values of proton spin-lattice relaxation time in the rotating frame (T1ρH), which is indirectly determined from the intensity decay of each resolved carbon.
3. Results and Discussion
The nanocomposites obtained were characterized by solid state nuclear magnetic resonance relaxometry. The determination of proton spin-lattice and spin-spin relaxation times was carried out to evaluate the clay exfoliation and intercalation.
a) Spin-lattice relaxation time―T1H
As described before, spin-lattice relaxation parameter, T1H, is very much influenced by paramagnetic effects from metals present in the clay structure (iron) as previously demonstrated by Vander Hart, 2001 and Almeida, 2010. It is known that the dominant mechanism of proton relaxation process is dipole-dipole interaction; however some contribution of chemical shift anisotropy and molecular translation-diffusion is also observed in the behavior of this parameter.
Table 1 shows the T1H values for HIPS and the nanostructured materials containing S7 in different ratio.
The decrease in the relaxation time values for all the samples containing clay, when compared to HIPS, is assumed to be related to the new structures formed after the nanoparticle addition and the influence of the paramagnetic metals present in the clay structure. The observed decrease was attributed to the predominance of exfoliation process, since in this structure the polymer chains are around the clay lamellae and they are intimately mixed to each other. For the samples with 2% and 3% of clay it was observed a sum of paramagnetic effect and the dominant mechanisms of relaxation process; we postulate that a short spatial proximity exists between the macromolecules and the metals in these samples. These observations are consistent with the organoclay being better dispersed and distributed in the polymer matrix of these samples.
b) Spin-lattice relaxation time in the rotating frame―T1ρ
It is known that T1ρH is measured directly in the cross polarization experiments by a series of 13C CPMAS spectra in which the contact time is incrementally increased. T1ρ depends on lattice motions to induce transitions the proton-proton dipolar coupling. The dominant relaxation mechanism, dipole-dipole, has a pronounced influence in the behavior of this parameter, consequently the influence of paramagnetic metals is minimal.
Figure 1 shows the decay of the C-1 carbon as a function of contact time for the HIPS and for the nanostructured materials containing 1-3% w/w of clay. The lines are fitted using the Ordinary Least Squares (OLS) model and all decays were fitted employing the Equation 2 with R2 ≥ 0.91 to obtain T1ρH values.
Knowing that the value of spin-lattice relaxation time in the rotating frame is obtained from the slope of the tangent curve to the decay, this parameter is predominantly sensitive to spectral density modulation dipole. A fast decay refers to a value of shorter time due to rigidity of the system. Examples (c) and (d) in Figure 1 display this behavior.
Table 2 shows the T1ρH values for HIPS and the nanostructured materials containing clay in different ratio.
The fluctuation in the T1ρH values could be explained by the morphology formed after the clay addition and the proportion of the nanoparticle in the systems. The major impact was observed in the sample containing 1%
Table 1.Values of spin-lattice relaxation, T1H, plotted with one exponential for HIPS and the nanostructured materials obtained.
Table 2. Values of spin-lattice in the rotate frame relaxation, T1ρH, plotted with one exponential for HIPS and the nanostructured materials.
of clay which could be related to the dispersion of the clay lamellae in the polymer matrix. This value suggests that the intercalation process, which would have lower amount of lamellae dispersed, allows for more degree of molecular freedom when compared with the other systems, possibly due to less interference of the clay lamellae in the rigidity of the matrix. However, the systems containing 2% and 3% of clay showed smaller variation in the value of T1ρH, albeit showing more degree of exfoliation. It is interesting that the system with 2% of clay




Figure 1. Decay obtained by the variation of the contact time for determining the value of T1ρH for HIPS (a) and for the nanostructured materials with 1% (b), 2% (c), and 3% (d) of clay.
displayed more degree of exfoliation than the one with 1%, suggesting a better interaction between the clay and the matrix. Nevertheless, the inhomogeneity of the T1ρH values points to the mixed composition of these systems, where intercalated, exfoliated, and polymeric phases coexist.
c) Spin-spin relaxation time―T2
In the T2 parameter the degree of relaxation is determined by the molecular motion, primarily rotation rates, of the dipoles compared to the Larmor frequency. In this case the predominant mechanism is dipole-dipole; therefore some contribution of chemical shift anisotropy and surface relaxation that assume a fast diffusion regime [17] .
Table 3 exhibits the spin-spin relaxation values, fitted with one exponential, for polymer matrix and the nanostructured systems.
In the T2 relaxation mechanism there is an energy change between spins. It is also observed that, for this relaxation the paramagnetic effect of the iron present in the clay structure causes very low or no interference in the spin-spin relaxation process. Analyzing the T2 values obtained from one exponential measurement, the addition of 1% of clay decreases the value of this parameter. An increase of dipole-dipole intermolecular interaction due to the increase in the spatial proximity, typical for a predominant intercalation process, could explain this behavior. However, the addition of 2% of clay behaves differently from 1%, the increase in the T2 value for this proportion suggestion that a surface relaxation process is occurring most likely due to the predominance of exfoliation process. As the amount of clay reaches 3%, the value of T2 drops again, indicating an increase of dipole-dipole intermolecular interaction, characteristic of a predominant intercalation process.
Figure 2 exhibits the domain curves of HIPS and the nanostructured materials.
Figure 2 implies the existence of two domains with distinct molecular mobility, pointing again to the heterogeneity of the materials obtained. One domain with higher values of T2 related to the mobile phase and other one related to the more rigid phase. The blank HIPS samples present two domains with distinct molecular mobility and near intensities. The nanocomposites samples show more heterogeneous systems with less intensity domains, with widened base lines in comparison to blank HIPS sample. The wideness of base line is interpreted as an increase in the heterogeneity. The 1% of filler shows a preference of clay to higher rigid phase. The 2% of clay
Table 3. Values of spin-spin relaxation fitted with one exponential.
Figure 2. Domain curves extracted from the T2 data of HIPS and the nanostructured materials.
Table 4. Values of spin-spin relaxation fitted with two exponential.
interfere more than the others ratios, probably because is better dispersed and distributed in the matrix, increasing the heterogeneity in both molecular mobility phases. Lastly, 3% of clay shows a decrease in the heterogeneity in the matrix. The contributions of these domains are displayed in Table 4 where the values of T2 were fitted with two exponential. The rigid domain (low T2 values―T2Hr) contributes with 98% of the domain sample, while the high molecular mobility domain (high T2 values―T2Hm) contributes with only 2% of the domain system.
The values of T2Hr, related to the rigid domains control the mechanism of relaxation process. They do not present significant changes in their proton T2 relaxation values, because they have low molecular mobility and the clay is probably not well dispersed in this phase. On the other hand, the T2Hm values of the high mobility domain change significantly compared with the matrix itself and each other. In this region the chains have more freedom to move and consequently are more susceptible to the influence of clay dispersion and distribution, as well as the surface relaxation process.
Analyzing the behavior of T2Hm, the decreased in this parameter value, for the samples containing 1% and 3%, indicates that there is predominance of intercalation process, due to the decrease in the molecular mobility, as the chains are intercalated among the clay lamellae they do not have freedom to move, being constricted among them. In contrast, with 2% proportion there is a predominance of exfoliation process, since in the exfoliated structure the chains have higher degree to move around the clay lamellae and this freedom increases the spin-spin relaxation data.
NMR relaxometry proved to be a good tool to evaluate polymer nanomaterials according to the changes in the relaxation time values comparing to the polymer matrix before the incorporation of the nanoparticles.
4. Conclusions
The nanomaterials of HIPS and OMMT were successfully obtained and the nanoparticle was dispersed in the polymer matrix, using the solvent cast method. It was also verified that the addition of 2% of OMMT showed a better dispersion and distribution in the polymer compared to the others proportions.
According to the relaxation time values, the best quantity of nanoparticle to be well dispersed and distributed in the polymer matrix is 2%. In this proportion, a higher degree of exfoliation process occurred, based on the decrease in the relaxation time, attributed to the relaxing effect of the paramagnetic metal present in the clay structure. These metals can display a direct influence in the proton relaxation by decreasing it, which is consistent with an exfoliation process.
The proton NMR relaxation data showed that the polymer nanomaterials investigated presented good organoclay dispersion and distribution in the polymeric matrix, promoting a formation of mixed nanocomposite structure containing part exfoliated and part intercalated.
Acknowledgements
We thank CNPq, CAPES, FAPERJ and Petrobras for financial support.
Cite this paper
Paulo Sérgio Rangel Cruz da Silva,Lívia Rodrigues Menezes,Maria Inês Bruno Tavares, (2016) The Influence of Organo-Clay Ratio in the HIPS-OMMT Nanocomposites Analyzed by Proton Spin-Lattice and Spin-Spin Relaxation Times. Materials Sciences and Applications,07,150-158. doi: 10.4236/msa.2016.73015
References
- 1. De Andrade, F.D. and Colnago, L.A. (2012) Uso da RMN como um sensor online em processos industriais. Quimica Nova, 35, 2019-2024. http://dx.doi.org/10.1590/S0100-40422012001000023
- 2. Inês Bruno Tavares, M., Freitas Nogueira, R., Aguiar da Silva San Gil, R., Preto, M., Oliveira da Silva, E., Bruno Rocha e Silva, M., et al. (2007) Polypropylene-Clay Nanocomposite Structure Probed by H NMR Relaxometry. Polymer Testing, 26, 1100-1102.
http://dx.doi.org/10.1016/j.polymertesting.2007.07.012 - 3. Kickelbick, G. (2007) Hybrid Materials: Synthesis, Characterization, and Applications. Wiley [Internet].
- 4. Stejskal, E.O. and Memory, J.D. (1994) High Resolution NMR in the Solid State: Fundamentals of CP/MAS. Oxford University Press.
- 5. McBrierty, V.J. and Packer, K.J. (2006) Nuclear Magnetic Resonance in Solid Polymers. Cambridge University Press.
- 6. Nogueira, R.F., Tavares, M.I.B., San Gil, R.A.S. and Da Silva, N.M. (2005) Solid State NMR Investigation of Polypropylene/Brazilian Clay Blending Process. Polymer Testing, 24, 358-362. http://dx.doi.org/10.1016/j.polymertesting.2004.10.005
- 7. Rodrigues, T.C., Tavares, M.I.B., Preto, M., Soares, I.L. and Moreira, A.C.F. (2008) Evaluation of Polyethylene/Or- ganoclay Nanocomposites by Low-field Nuclear Relaxation. International Journal of Polymeric Materials and Polymeric Biomaterials, 57, 1119-1123.
http://dx.doi.org/10.1080/00914030802428716 - 8. Merat, P.P., Tavares, M.I.B. and da Silva, E.O. (2011) Preparation of Polycarbonate/Clay Nanocomposite and Characterization by X-Ray, Thermal Analyzes and Low-Field Nuclear Magnetic Resonance. Journal of Materials Science and Engineering, 1, 671-677.
- 9. dos Santos Almeida, A., Bruno Tavares, M.I., da Silva, E.O., Cucinelli Neto, R.P. and Moreira, L.A. (2012) Development of Hybrid Nanocomposites Based on PLLA and Low-Field NMR Characterization. Polymer Testing, 31, 267- 275.
- 10. Komoroski, R.A. (1986) High Resolution NMR Spectroscopy of Synthetic Polymers in Bulk. VCH Publishers.
- 11. Levitt, M.H., Grant, D.M., Harris, R.K. and Wiley, J. (2002) Encyclopedia of Magnetic Resonance. Encycl. Nucl. Magn. Reson.
- 12. Schaefer, J., Sefcik, M.D., Stejskal, E.O. and McKay, R.A. (1984) Carbon-13 T1ρ Experiments on Solid Polymers Having Tightly Spin-Coupled Protons. Macromolecules, 17, 1118-1124. http://dx.doi.org/10.1021/ma00136a002
- 13. Parmer, J.F., Dickinson, L.C., Chien, J.C.W. and Porter, R.S. (1987) Polymer-Polymer Miscibility Determination via CP-MAS NMR in Blends of Deuteriated and Protonated Polymers. Macromolecules, 20, 2308-2310. http://dx.doi.org/10.1021/ma00175a042
- 14. Bovey, F.A. and Mirau, P.A. (1996) NMR of Polymers. Academic Press.
- 15. Casanova, F., Perlo, J. and Blümich, B. (2011) Single-Sided NMR. Springer. http://dx.doi.org/10.1007/978-3-642-16307-4
- 16. da Silva, P.S.R.C. and Tavares, M.I.B. (2015) Solvent Effect on the Morphology of Lamellar Nanocomposites Based on HIPS. Materials Research, 18, 191-195. http://dx.doi.org/10.1590/1516-1439.307314
- 17. Ronczka, M. and Müller-Petke, M. (2012) Optimization of CPMG Sequences for NMR Borehole Measurements. Geoscientific Instrumentation, Methods and Data Systems Discussions, 2, 507-538. http://dx.doi.org/10.5194/gid-2-507-2012




