Received 21 April 2015; accepted 26 May 2015; published 29 May 2015

ABSTRACT

Crystallinity refers to the degree of structural order in a solid and has a big influence on hardness, density, transparency and diffusion. Even within materials that are crystalline completely, the degree of structural perfection can vary, reflecting size and elastic strain of many independent crystalline regions (grains or crystallites) of which these materials are composed. In this work it was attempted to reduce the crystallinity of human enamel using a technique of mechanical grinding (MG) with an ultra-compact FRITSCH Mini-Mill PULVERISETTE 23 machine. Variation in the crystallinity through the MG was monitored by X-ray diffraction (XRD) by broadening of the diffraction peak and examined using the Williamson-Hall plot method. Crystallites in human enamel are regularly arranged and oriented (in the [001] direction) perpendicularly to the interface of enamel- dentin junction. The results showed an anisotropic feature in crystallinity. Reduction of the crystallinity along the a-axis is due to the crystal strain rather than to the refinement of crystal, and vice versa along the c-axis. After 230 h of the MG, the length of crystallites decreased from 100 nm to 30 nm and width from 40 nm to 37 nm approximately.

Keywords:

Human Tooth Enamel, Crystal Structure, Mechanical Grinding, X-Ray Diffraction, Crystallites

1. Introduction

Since the main mineral component of natural teeth, bone and hard tissues was identified as calcium phosphate, mostly in the form of hydroxyapatite [HAp: Ca₁₀(PO₄)₆(OH)₂ ], it has been widely synthesized and used as a biocompatible ceramic in many areas of biomedical applications. As it is well known, the biochemical properties and the crystal structure of biological apatite such as human tooth enamel are significantly different from those of synthetic apatite ceramics composed of pure HAp [1] -[4] . Moreover, synthetic HAp material can be prepared only as micro or nano crystalline powder. Therefore, powder X-ray diffraction (XRD) is an indispensable tool to gain a better understanding and characterization of the solid-state properties of these materials and a large volume of literature has been devoted, between all, to the measuring particle size of synthesized powders using XRD data [5] [6] . Therefore, it is possible to say that on this day, research of the crystallinity by XRD refers to crystal size and/or strain analysis more than to volume percentage of crystalline phase in a HAp material. Unfortunately, for obtaining an accurate crystallite size there is no a simple XRD method for not only human tooth enamel, but also synthesized powders. To achieve this goal, recent studies have been focused on modeling the crystal structure of synthesized powders using Rietveld refinement techniques and computer simulations no matter how difficult it is [7] .

For this purpose, diffraction theory predicts that the line broadening (peak width) of a powder XRD pattern will be very sharp for a crystalline material consisting of sufficiently large, randomly oriented, and strain-free crystallites [8] , thus, the inverse correlates with crystal size and lattice perfection. In the simplest case where the particles are stress-free, the crystallite size can be estimated from a single diffraction peak using the Scherrer equation [9] :

where λ is the wavelength of the monochromatic X-ray beam, B(θ) is the Full Width at Half Maximum (FWHM, in radians) of the peak at the maximum intensity, θ is the peak diffraction angle that satisfies Bragg’s law for the hkl plane and t is the crystallite size. It should be noted that the size of the crystallites measured using the XRD technique is a volume average of the crystal thickness in the direction normal to the reflecting planes and not an actual geometrical characteristic of the particles forming the mineral phase of material.

In those cases where stress may be present, a more robust method involving several diffraction peaks is required. The most common method of strain/size analysis utilizes the fact that the broadening from the two different sources has different angular relationships. For instance, the size broadening has a 1/cos(θ) relationship while the strain follows a tan(θ) function. The total broadening can be described using the Williamson-Hall equation [10] :

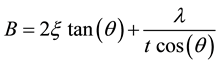
where ξ is the integral breadth of the strain distribution (corresponding to the broadening of the diffraction peak). Finally, the instrument and the temperature factors also contribute to the broadening. If we assumed that the observed peak profile is a convolution of the profiles from all of these contributions, where broadening functions have Gaussian distributions, the Williamson-Hall equation can be written as:

where e corresponds to microstrain (, d is the lattice spacing), K is a constant (»0.9) and Bt² is

an instrumental broadening due to α₁, and α₂, which depends on the 2(θ) value. For example, in the case of HAp,

for (002), Bt² » 0.03˚, whereas for (004), Bt² » 0.07˚. Plotting vs sin(θ), the crystallite

size t is extracted from the intercept with the ordinate N and the microstrain is determined by the slope of the line, as presented in Figure 1. It should be noted that this method requires at least two data points according to the index of its reflection, for example, several h00 reflections in the [100] crystal direction.

As it is well known, powder XRD is a destructive technique to study human enamel and all information of the natural tooth structure is lost because a sample must be previously milled into a fine powder. In addition, it requires a considerable amount of sample powder to generate diffraction patterns.

The newly developed microdiffraction equipment, such as the high resolution XRD equipped with a general area detector diffraction [11] , makes it possible to analyze a tooth in situ without destruction. Moreover, it has been possible to apply this non-destructive technique in carious and normal selected microzone areas [11] . Unfortunately, like all local techniques, crystal X-ray microdiffraction analysis has some disadvantage for characterization of the human tooth enamel due to two main reasons. First, each natural tooth has its own individual structure, which does not repeat itself in other zones of the same tooth. Second, as it is well known, the crystallites in human enamel are regularly arranged, so they produce an anisotropic X-ray intensity distribution (texture) [12] that gives the greatest possible source of error to the study of crystallinity with this method [13] .

With such simple method as the MG, the regular crystal arrangement in the human tooth enamel has been destroyed and studied its crystallinity by the powder X-ray diffraction methods. Before this, tooth enamel was also studied by the crystal X-ray diffraction methods. Some useful results in this paper are reported.

2. Experimental Procedure

2.1. Sample Preparation

Enamel powder was obtained from non-carious parts of four human molars and premolars, fully developed and extracted for orthodontic reason. These parts were ground with an agate pestle in a small agate mortar. After that, the enamel powder was sieved for quantitative particle size analysis using the 120 (125 µm) and 325 (44 µm) mesh-per-inch sieves. The sieved powder was later mechanically ground using the ultra-compact FRITSCH Mini-Mill PULVERISETTE 23 with two agate balls (10 mm in diameter) in a tempered steel container (volume 10 ml). About 600 mg (or about 0.5 ml of the sample volume) of enamel powder were charged in the container (stainless steel grinding bowl) and ground through impact between the grinding balls and the inside wall of the container by 2000 oscillations per minute at amplitude of 9 mm for an appropriate period, being 230 h as the longest time.

For crystal XRD studies, two enamel pieces (bulk samples) of about 2 mm thick with different orientations relative to the tooth’s surface (transversal, E, and longitudinal, Z) were obtained from a healthy human molar tooth using a low-speed diamond saw equipment (Isomet, Buehler). Surface’s samples were mirror-end polished with silicon carbide paper and alumina slurries in a grinder-polisher (Minimet, Buhler). A light microscope (Carl Zeiss model Axiovert 25) was used in this process.

2.2. X-Ray Diffraction Analysis

The crystal structure characterization and the texture maps were made using a Panalytical X’Pert PRO MRD diffractometer with Ni filtered CuKα radiation generated at 45 kV and 20 mA. The diffraction intensity as a function of the angle 2-theta was measured between 20˚ and 90˚, with a 2-theta step of 0.039˚. A CCD solid-state detector in scan mode was used. This mode allows making a single scan in 16 minutes averaging 10.8 seconds per point. The texture pole figures were made using the following: a Soller slit (0.04 rad), divergence slit (1/2˚), parabolic X-ray mirror in the incident beam path and a Soller slit (0.04 rad), parallel plate collimator (0.27˚), point detector with a large window in the diffracted beam path.

The powder X-ray diffraction patterns were measured with a Bruker D-8 ADVANCE diffractometer using the Bragg-Brentano 0 - 0 geometry with Ni-filtered CuKα radiation and a 1-dimensional position sensitive silicon strip detector (Linxeye, Bruker). The diffraction intensity as a function of the angle 2-theta was measured between 6.5˚ and 110˚, with a 2-theta step of 0.039˚, for 52.8 s per point.

3. Results and Discussion

3.1. Bulk Enamel Samples

The XRD patterns of bulk samples in transverse (sample E) and longitudinal (sample Z) directions are shown in Figure 2. This figure shows that for all diffraction lines, X-ray intensities of peaks with the same hkl indices are different and they are even different from those of synthetic HAp (PDF cards: 00-009-0432 or 00-024-0033). This result strongly suggests a regular arrangement in the HAp crystals of human tooth enamel, which is in well agreement with the results by other methods [14] . It should be noted that each natural tooth has its own individual enamel curvature, so all X-ray diffraction patterns for different zones of the same tooth will be different [11] , [15] . In our samples, the effect of texture produced an increment in height of the (002), (102), (112), (202), (213), and (004) peak intensities in the transverse direction (sample E), while the (002), (102), and (004) peaks are not observed in the longitudinal directions (sample Z).

For analyzing the textured order in the transverse and longitudinal directions of these samples, the (002), (112), (202) and (002), (121), (300) peaks were observed respectively. After correcting a “defocusing effect” for all pole figures, we detected that only the [002] direction is the main preferential direction in both samples, as seen in Figure 3 corresponding to the {0001} basal texture that is frequently presented in the hexagonal materials [16] . These results suggest the HAp crystallites in the bulk enamel samples are arranged regularly, with their c axis along the longitudinal direction of the tooth and perpendicular to the interface of the enamel-dentin junction.

Using the Williamson-Hall equation for the XRD pattern of the sample E, the particle size along the c-axis and the micro strain calculated from the width of (002) and (004) peaks were 88 nm ±1 nm and 0.93%, respectively.

3.2. Crushed and Sieved Powder Enamel Samples

Figure 4 shows two XRD profiles of the enamel powder after sieving with different mesh sizes but before mechanical grinding. As expected, all diffraction peaks appeared and their positions were observed completely similar to each other. However, not all peak intensities of these powders are similar. In fact, the powder consisting from particles sieved through the smallest mesh should give a diffractogram with broader peaks than the powder consisting from particles that were sieved through the largest mesh. In spite of this, Figure 4 shows that the intensity of the (002), (112) and (202) diffraction peaks for the powder obtained by the mesh #325 are higher than the powder obtained by the mesh #120. Moreover, for the powder obtained by the mesh #120 the intensity of the (300) peak is higher than the intensity of the (211) peak, which has 100% of peak intensity for all XRD synthetic HAp patterns. These results suggest that the effect of a regular arrangement in the enamel powder is conserved in particles having an average size from 44 to 125 micron.

As the crystallites of human tooth enamel have a “prism” likely shape, their size is reported to vary depending on the (002) and the (300) peak intensities. So, the FWHM of (002) and (004) reflections characterize the length

(c-axis) of these prisms and the FWHM of (100) or/and (200) and (300) reflections characterize its width (a-axis). They should be applied for the studies of crystallinity by the Williamson-Hall plot method.

Using the Williamson-Hall equation for XRD patterns of these powders, the particle size along the c-axis, along the a-axis and the microstrain of the crystallites were estimated. The two XRD patterns showed the same average length of the crystallites (about (102 ± 1) nm) and the same average width (about (42 ± 1) nm). The microstrains of the crystallites were different not only along the c-axis and along the a-axis but for the two powders. The values of the microstrain for the powder sieved by the mesh #120 was 0.78% along the c-axis and 0.18% along the a-axis while the microstrain for the powder sieved by the mesh #325 was 0.75% along the c-axis and 0.195% along the a-axis. This would explain the difference of peak intensities observed in the XRD patterns.

Figure 5 shows the Z-contrast-STEM image of an enamel powder grain after hand crushing. As seen in this figure, the particle is of about 600 nm in the size and it is composed of individual crystals of 100 - 150 nm along the c-axis and 20 - 40 nm along the a-axis, approximately. According to our analysis, and comparing these results with those commented in section 3.1, it is clear that the crystal XRD method gives values that differ from those obtained by the powder XRD method because of a regular crystal arrangement in the tooth enamel and, therefore, cannot be applied for the studies of crystallinity.

3.3. MG Powder Enamel Samples

The crystallinity of the human tooth enamel has been reduced by using the MG for 230 hours in total. Figure 6 shows the XRD patterns for 30, 60, 90, 200, and 230 h, respectively. After 200 hours of the MG (not shown) and 230 hours, the XRD patterns were practically the same. Figure 7 shows the SEM image of the powder after 230 h of the MG.

It has been found out that, depending on the form of individual crystallites, crystallinity of human tooth enamel varies with milling time. Figure 8(a) shows the Williamson-Hall plot for the (002), (004) peaks of the MG powders from where particle size along the c-axis and the microstrain of the crystallites were estimated. As shown in this figure, the crystal length decreased rapidly from 100 nm to 40 nm in the first 30 h of the MG, and then it slowly changed to 30 nm for 230 h. Therefore, after 30 h of the MG, the length of the crystallites changed from 100 nm to 30 nm, approximately. However, the growth of residual elastic strain is rather small: from 0.25% for 30 h and 0.48% for 230 h of the MG. Moreover, while the value of the microstrain along the c-axis for the powder consisting from particles sieved through the mesh #120 is 0.78%, its value after 30 h of the MG is only 0.25%. This explains the increase of the (002) and (004) peak intensities for the XRD pattern after 30 h of the MG (Figure 6).

On the other hand, the crystal width slowly decreased in the early stage of the MG from 40 nm to 37 nm in 30 h, and then practically did not change after 230 h (Figure 8(b)). However, growth of the residual elastic strain is rather large: from 0.27% for 30 h of the MG to 0.69% for 230 h.

Therefore, decrease in crystallinity in the a-axis is due to crystal strain rather than to the thinning of crystals. Figure 9 shows the change of the crystal strain in the MG powders along the a- and c-axes. This result strongly suggests an anisotropic feature of the human tooth enamel crystallinity, as it is predominantly determined by both of the two important factors: crystal size (its length and width) and residual elastic strain.

In addition, the results showed that texture in the tooth enamel plays an important role not only in the studies of the crystallinity by X-ray diffraction, but also improves the crystallinity itself.

4. Conclusion

This study pointed out the importance of the textured arrangement of human tooth enamel crystals. These crystallites are regularly arranged and oriented in the [001] direction, perpendicular to the interface of the enamel- dentin junction. The crystallinity of human enamel has the anisotropic characteristic and depends on the direction of the individual crystallites that compose the tooth enamel. With the Williamson-Hall plot, the average size of the individual crystallites (about 100 nm along the c-axis and about 40 nm along the a-axis) can be easily obtained by the powder XRD characterization. However, it is worth to mention here that these results cannot only be attributed exclusively to the particle size or only to the strain of the individual crystallites, but also to an effect of texture, crystallite boundaries, and amorphous hydroxyapatite contributing to the properties of human enamel to resist wear and fracture. This fact is an important input for synthesizing new biocompatible ceramics composed on synthetic HAp with better biochemical properties.

Acknowledgements

The authors acknowledge the technical assistance from P. Mexía Hernández, A. Morales, C. Zorrilla, and A. Tavira Fuentes. O. Koudriavtseva is grateful to the postdoctoral support from CONACYT. This work was supported by DGAPA-UNAM under project IN106710.

References

NOTES

^*Corresponding author.