Materials Sciences and Applications
Vol.4 No.8A(2013), Article ID:35815,6 pages DOI:10.4236/msa.2013.48A002
Evaluation on Feasibility of Sintered Cattle Bone Powder as a Heavy Metal Adsorbent
![]()
1Department of Environmental and Chemical Engineering, Seonam University, Namwon, South Korea; 2Korea Urban Regeneration Technology Institute, Jeonju, South Korea.
Email: kwak124@hanmail.net; mshankim@hotmail.com
Copyright © 2013 Dong-Heui Kwak, Mi-Sug Kim. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 14th, 2013; revised July 15th, 2013; accepted July 24th, 2013
Keywords: Adsorption; Cattle bone; Bone charcoal; Heavy metal; Isotherm
ABSTRACT
Quite some bones of cows and pigs are discharged from home and restaurant industry as food wastes after cooking by boiling. This study conducted adsorption experiment of heavy metals using waste bones as an absorbent for recycling the waste bone and evaluated its feasibility. Sintered cattle bone (SCB) was manufactured in powder form after sintering at 550˚C - 600˚C and pulverizing, and crystal structure examined by XRD was similar to synthetic hydroxyl apatite. Adsorption equilibrium of single component such as Pb, Cd, and Zn was able to be expressed by isotherm equations of Langmuir, Freundlich, and Sips. Among them, Sips isotherm was accorded best. Also, IAST (ideal adsorbed solution theory) was used to predict multi-component adsorption equilibrium and correlation between those predicted values and empirical values was satisfactory. Adsorption affinity on SCB was in order of Pb, Cd, and Zn and it was corresponded with cases of activated carbon or synthetic hydroxyapatite. Finally, this study confirmed feasibility of SCB as an adsorbent of the heavy metal in real field of wastewater treatment.
1. Introduction
Studies about estimating performance and designing an adsorption system are divided into mass transfer and selection of adsorption model. In separation operation by adsorption, a fundamental thing is adsorption equilibrium relationship [1]. However, the adsorption equilibrium theory underlying analysis of process optimization is still in a slight level, while separation and purification by an adsorption process are continuously developing. Also, adsorption models are required the theory related to more realistic adsorption phenomena. Most of studies on the adsorption process are considered for an ideal condition or non-ideal adsorption system with the ideal theory. Results indicate that many cases bear no resemblance to reality. In real, it is very difficult to apply directly for analysis of process even though the proper adsorption isotherm is existed in the non-ideal adsorption system.
The adsorption isotherm for a single component (mono-adsorption isotherm, hereafter) is formulized by experimental data and includes Langmuir isotherm [2], Freundlich isotherm [3], Sips isotherm [4], and so on. In general, Langmuir isotherm is suitable when surface of adsorption is uniform and Freundich isotherm or Sips isotherm is more proper when surface energy of the adsorption is not in uniform distributed [5]. The mono-adsorption isotherm in the adsorption system has been progressed not only the theoretical study but also the experimental works and lots of adsorption isotherm have been also developed. However, real adsorption processes are adopted for multi components. Therefore, more studies about adsorption equilibrium of multi components (multiadsorption equilibrium, hereafter) are very important. Various adsorption equilibrium theories of the multi component reported until now are potential theory [6], ideal adsorption solution theory [7], empty seat theory [8,9], and so on. Recently, plenty of theories as well as real adsorbed solution theory in print consider non-ideality but they cannot apply for analyzing the real processes. The proper multi component theory for the real process analysis is required its simplification and accurate prediction of the multi-adsorption equilibrium.
Langmuir isotherm, Freundlich isotherm, and Sips isotherm are selected as the mono-adsorption isotherm. Ideal adsorbed solution theory (IAST) was selected as the multiadsorption equilibrium model for predicting in this study.
Ultimate goals for the adsorption study are to simulate behavior of adsorbates in the adsorption process and to develop an analysis method of the adsorption process and to predict process efficiency and an absorbent life accurately based on previous studies related to material properties and characteristics of adsorbents, the adsorption equilibrium theory, transfer phenomena of adsorbates in the adsorption process, a mass balance equation of the adsorption process, and so on. Without laboratory experiments, the model is able to predict operation condition for change of the adsorbent’s properties and operating variables. Thus, this study considers the adsorption equilibrium characteristics for the waste livestock bone as a part of fundamental studies for development of the adsorption process and feasibility of waste livestock bone sintered at high temperature as an adsorbent.
2. Adsorption Isotherm Theory
In general, empirical adsorption isotherm is for estimating adsorption capacity, predicting the adsorbent’s life, using analysis of behavior and design of the adsorption system, and providing enough information including heat of adsorption. To predict adsorption equilibrium of the single component (mono-adsorption equilibrium, hereafter) is very important in studying interactions between the adsorbent and the adsorbate or adsorbates. The monoadsorption equilibrium is described in simple adsorption isotherm with two or three parameters and representative isotherms are as in the following:
Langmuir
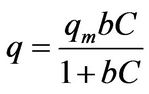 (1)
(1)
Freundlich
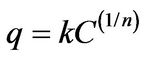 (2)
(2)
Sips
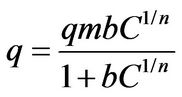 (3)
(3)
Langmuir isotherm is for uniform distribution of adsorption surface energy, Freundlich isotherm is more suitable than Langmuir isotherm for un-uniform surface of the adsorption, and Sips proposes adsorption isotherm combining Langmuir isotherm and Freundlich isotherm to explain most of adsorption equilibrium covering relatively broad concentration ranges.
On an assumption that phases adsorbed on adsorbent surface form an ideal solution, fundamental equations governing adsorption equilibrium of the multi components (multi-adsorption equilibrium) are as in the following.
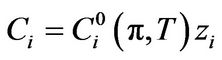 (4)
(4)
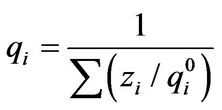 (5)
(5)
 (6)
(6)
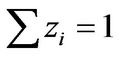 (7)
(7)
 (8)
(8)
where zi is mole fraction of i component in the adsorption phase, qT is overall adsorption quantity, and superscript 0 is concentration of the single component at spreading pressure. The spreading pressure of each component can be calculated as below,
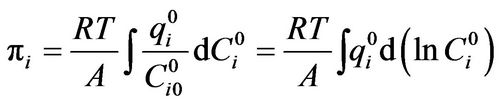 (9)
(9)
If the mono-adsorption isotherm is same as below, the spreading pressure can be obtained.
Lanmuir
 (10)
(10)
Freundlich
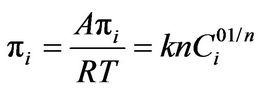 (11)
(11)
Sips
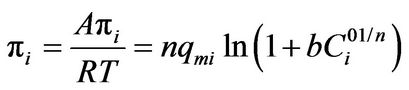 (12)
(12)
A condition when a base of IAST is reached is that all spreading pressures(πi) are equal. Given conditions, adsorption calculation of the multi components can solve simultaneous equations (5)-(9) [10,11]. An advantage of IAST is to seek the multi-adsorption equilibrium quantity without other conditions if parameters of the mono-adsorption isotherm. Also, many previous studies are reported that IAST can well explain the adsorption system of many multi components in modest heterogenity [12].
The purpose of the multi components adsorption process is to remove specific substances from a mixture solution more than the mono-adsorption process. Therefore, the multi-adsorption equilibrium theory needs to be organized. Because it consumes much time and a boring job in seeking the multi-adsorption equilibrium data in empirical way, attempts to predict the multi-adsorption equilibrium quantity have been continuously using the single or binary adsorption equilibrium data.
3. Materials and Methods
3.1. Adsorbent and Adsorbate
This study used waste cattle bones as an adsorbent. The waste cattle bone was treated as combusting for 3 hours at temperature 550˚C - 600˚C of an electric furnace after washing clearly with distilled water and sorted into 17 - 25 mesh sizes for using. Adsorption equilibrium experiments were performed with sintered cattle bone (SCB). SCB was prepared for experiments as combusted at high temperature to remove surface impurity and then removed all kinds of organic matters completely. SCB for the experiments was consisted of only bone tissues containing inorganic matter finally.
Three kinds of heavy metals, Pb, Cd, and Zn, were selected as the adsorbate. The selected heavy metals were washed with a solution prepared as diluting 1000 ppm Atomic Absorption Standard solution(in 1 mol/ℓ HNO3, Junsei chemical Co., JAPAN) with distilled water (over 18 mΩ). Also, concentration of each component was 3 - 5 mol/m3 for the mono-adsorption equilibrium experiments and overall concentration of each component was 2 mol/m3 for the multi-adsorption equilibrium experiments.
3.2. Experiment Methods
The mono-adsorption equilibrium experiment was progressed according to following procedure; the first step was to put a certain amount of the adsorbent (0.1 - 1.0 g) into a 50 ml tube contained 10 - 40 ml of a mixture solution, second step was to put a stopper on top of the tube, next step was to leave it in a constant temperature water tank keeping 20˚C with mixing for 3 hours, and then final step was to analyze residual concentration of filtrate. According to pilot experiment results, three hours were enough to reach the adsorption equilibrium. The heavy metal was analyzed by Inductivity Coupled Plasma Emission and details of instruments used for other analysis were indicated in Table 1.
4. Results and Discussion
4.1. Sintered Cattle Bone Powder
Figure 1 presented a X-ray diffraction analysis result for SCB. The X-ray analysis result corresponded roughly with hydroxyapatite Hap, Ca20(PO4)6(OH)2, and [libraray no. 9 - 432], and it showed similar peak types with the diffraction analysis result provided by Lee et al. [13] composing the sedimentation reaction method. According to Doi et al. [14], synthetic calcium apatite was dis-

Table 1. Instruments of analysis.
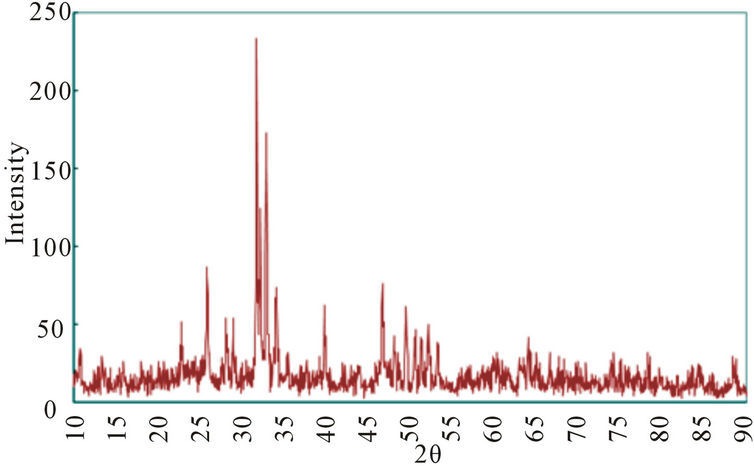
Figure 1. XRD peaks of SCB.
tinctively appeared the compressive strength, 211 and 112, at 31.8. 2θ and 32.0. 2θ. In comparison, SCB was about 210 and 125 at the same 2θ as shown in Figure 1. Those results confirmed that crystal structure and tissues had significant similarity between SCB and hydroxyapatite.
BET measurement results were average pore diameter (40.38 Å), surface area (35 m2/g), and pore capacity (2.73 × 10−2 cc/g) as shown in Figure 2.
4.2. pH Change
The change of pH indicated a growing trend gradually as SCB amounts were increased and Figure 3 presented pH change due to SCB doses. The previous pH growth was caused by increasing OH ion as dissolving hydroxyapatite in water partially.
However, pH of the solution was maintaining in acidity during the adsorption equilibrium experiment because the adsorbate, from the heavy metal st. sol to 1 mol/ℓ HNO3 stock sol, was strongly acid. If pH of the adsorbate solution is able to maintain in alkalinity due to using SCB in bulk when applying into the real wastewater treatment field, it may expect removal effect by sedimentation as well as adsorption.
4.3. Mono-Adsorption Equilibrium
The adsorption isotherm was decided depending upon the mono-adsorption equilibrium data. The selected adsorption isotherms were Langmuir isotherm and Freundlich isotherm for two parameters and Sips isotherm for three parameters. Parameters of the adsorption isotherms were determined by Less Square Method based on empirical data and results were appeared in Table 2.
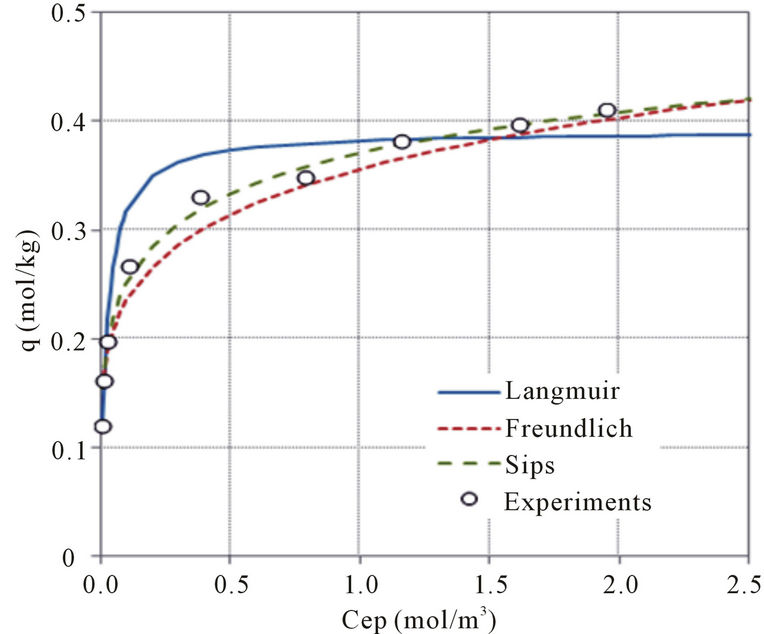
The adsorption isotherms obtained from each parameter were as shown in Figure 4. In the mono-adsorption equilibrium, Sips isotherm explained the mono-adsorption equilibrium data and it was more desirable than Frendlich isotherm or Langmuir isotherm. By the adsorption isotherm, the adsorption of Pb, Cd, and Zn also seemed to be very friendly. Adsorption affinity of the

Figure 2. Pore size of SCB (by BET).

Figure 3. pH change by SCB dosage.
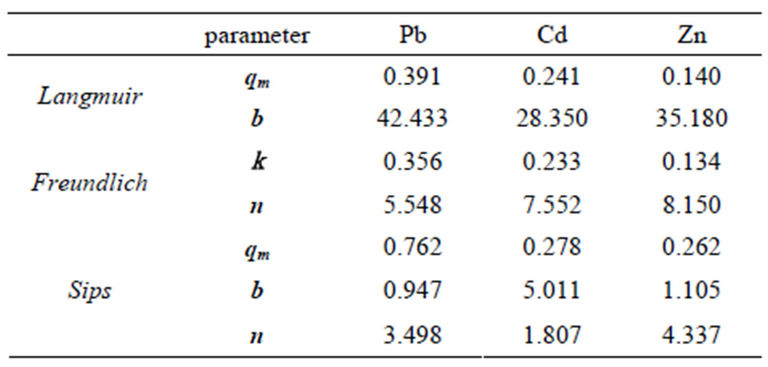
Table 2. Parameters of mono-adsorption equilibria data (Pb, Cd, Zn).
heavy metal on SCB was as in the following: Pb > Cd > Zn. This order was coincided with synthetic hydroxyapatite by the sedimentation reaction method in Lee et al. [13] and granular activated carbon in Doi et al. [14].
 (a)
(a)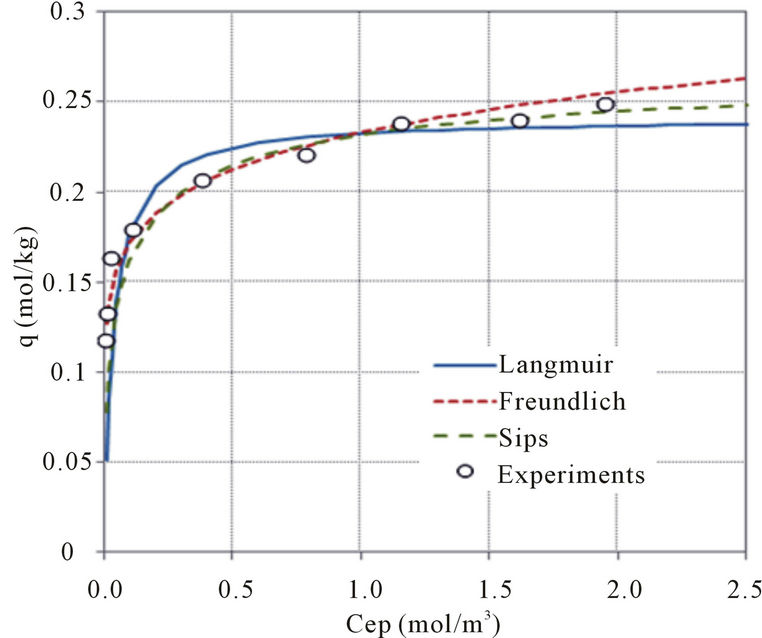 (b)
(b)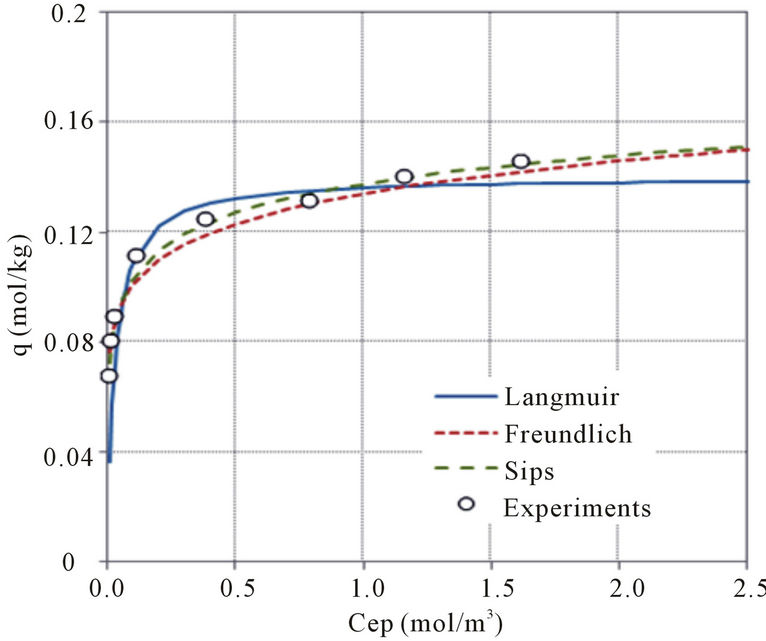 (c)
(c)
Figure 4. Adsorption isotherm of heavy metals on SCB. (a) pb; (b) Cd; (c) Zn.
4.4. Binary and Tertiary Adsorption Equilibria
The multi-adsorption equilibrium data as well as the mono-adsorption isotherm are required because the mixture solution containing more than two components is usually treated in removing pollutants using the adsorbent. However, it is not simple to obtain the multi-adsorption equilibrium data by the empirical way.
Based on numerous studies conducted until now, Ruthven et al. [12] report that IAST can explain well in the adsorption system composed with various heterogeneous multi components. This study estimated the multiadsorption equilibrium data based on IAST. An advantage of the selected theory was to get the multi-adsorption equilibrium quantity without any other conditions if the parameters of the mono-adsorption isotherm were known.
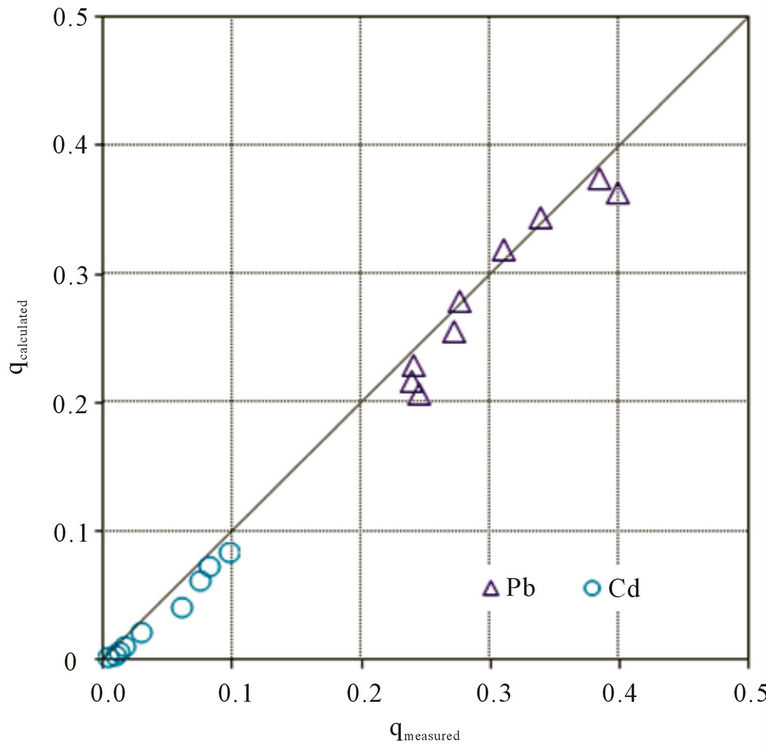
Three pairs (Pb-Cd, Cd-Zn, Zn-Pb) forming with three heavy metals (Pb, Cd, Zn) used in the mono-adsorption experiment and one trio (Pb-Cd-Zn) were performed competitive adsorption tests for the same adsorption time, 3 hours, as the mono-adsorption process. Also, Figure 5 compared between the empirical values and theoretical values, which were predicted from the selected IAST for the multi-adsorption equilibrium. In results, Pb indicated
 (a)
(a)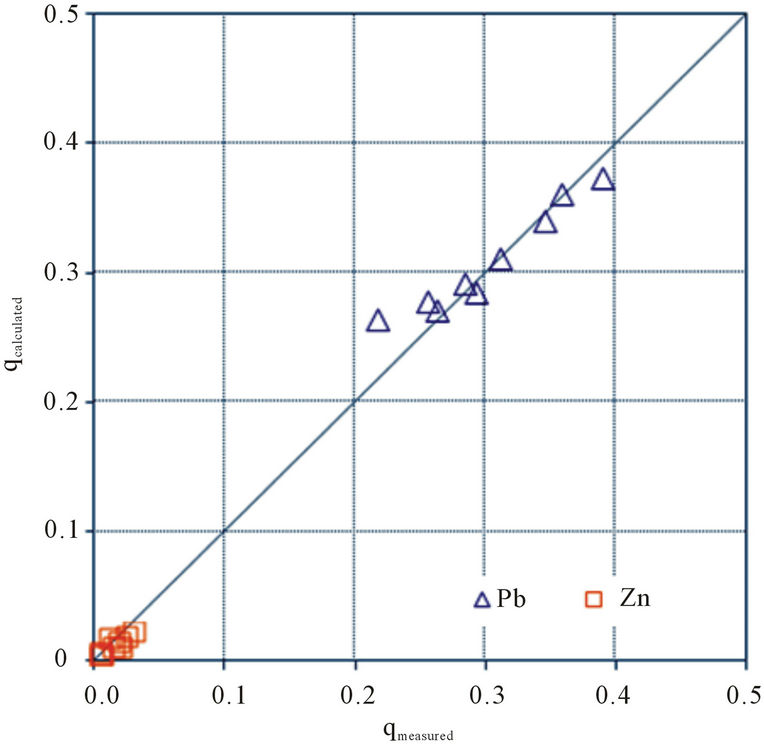 (b)
(b)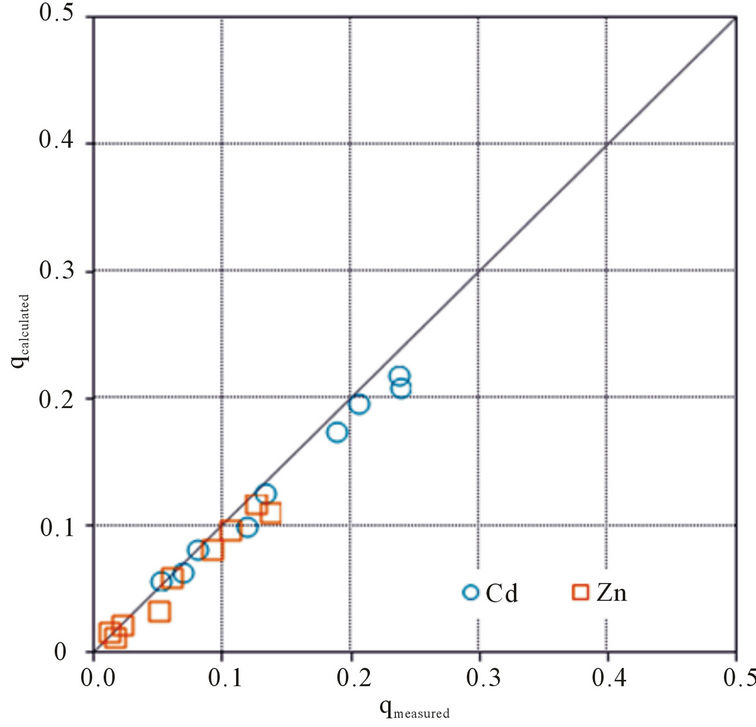 (c)
(c) (d)
(d)
Figure 5. Binary and tertiary adsorption equilibria of heavy metals on SCB. (a) Pb/Cd; (b) Pb/Zn; (c) Cd/Zn; (d) Pb/Cd/Zn.
large adsorption capacity and adsorption affinity in the mono-adsorption and also occupied lots of adsorption sites in the competitive adsorption. Therefore, Pb had stronger adsorption capacity than Cd or Zn, while Cd and Zn didn’t influenced by the competitive adsorption practically.
Also, great correlation between predicted and observed adsorption equilibrium was occurred and it proved the multi-adsorption equilibrium quantity could be determined with only parameters of the mono-adsorption isotherm.
5. Conclusion
This study conducted a series of experiments related to adsorption equilibrium for single component and multi components applying SCB sintered at 550˚C - 600˚C for 3 hours as an adsorbent. The adsorption equilibrium relation of each single component, Pb, Cd, and Zn on SCB was determined well by Sips isotherm and Langmuir isotherm or Freundlich isotherm also represented but not exact. This study obtained the great correlation between the empirical values and the predicted values by IAST, the multi adsorption equilibrium, for Pb, Cd, and Zn. The adsorption affinity of the heavy metal on SCB was in good order as following Pb > Cd > Zn and this order was coincided with cases of activated carbon and synthetic hydroxyl apatite. Therefore, this study emphasized feasibility of SCB as the adsorbent of the heavy metal in the real field of wastewater treatment.
6. Acknowledgements
This research (NRF-2012R1A1A4A01010342) was supported by the National Research Foundation of Korea (NRF) with grants from Ministry of Education in Korea, 2013.
REFERENCES
- W. G. Shim, J. W. Lee and H. Moon, “Performance Evaluation of Carbon Adsorbents for Automobile Canisters,” Korean Journal of Chemical Engineering, Vol. 15, No. 8, 1998, pp. 297-303. doi:10.1007/BF02707084
- I. Langmuir, “The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum,” Journal of the American Chemical Society, Vol. 40, No. 9, 1918, pp. 1361-1403. doi:10.1021/ja02242a004
- H. Freundlich, “Colloid and Capillary Chemistry,” 3rd Edition, Methuen, London, 1926.
- R. J. Sips, “On the Surface of a Catalyst Surface,” Journal of Chemical Physics, Vol. 18, No. 8, 1950, p. 1024. doi:10.1063/1.1747848
- H. Moon, S. K. Kook and H. C. Park, “Adsorption of Phenols onto a Polymeric Sorbent,” Korean Journal of Chemical Engineering, Vol. 8, No. 3, 1991, pp. 168-176. doi:10.1007/BF02706679
- W. Rudzinski and D. H. Everett, “Adsorption of Gases on Heterogeneous Surfaces,” Academic Press, London, 1994.
- R. T. Yang, “Gas Separation by Adsorption Processes,” Butterworths, Boston, 1987.
- A. L. Myers and J. M. Prausnitz, “Thermodynamics of Mixed-Gas Adsorption,” AIChE Journal, Vol. 11, No. 1, 1965, pp. 121-127. doi:10.1002/aic.690110125
- S. Suwanayuen and R. P. Danner, “A Gas Adsorption Isotherm Equation Based on Vacancy Solution Theory,” AIChE Journal, Vol. 26, No. 1, 1980, pp. 68-76. doi:10.1002/aic.690260112
- J. W. Lee, H. C. Park and H. Moon, “Adsorption and Desorption of Cephalosporin C on Nonionic Polymeric Sorbents,” Separation and Purification Technology, Vol. 12, No. 1, 1997, pp. 6-11.
- C. Tien, “Adsorption Calculation and Modeling,” Butterworth, Boston, 1994.
- D. M. Ruthven, “Principles of Adsorption and Adsorption Processes,” John Wiley & Sons, New York, 1984.
- M. S. Lee, C. K. Na, M. S. Lee, O. B. Kim and M. Y. Kim, “The Heavy Metal Adsorption Properties of Hydroxyapatite Powders Synthesized by Precipitation Reaction Method and Its Applicability for the Removal Agents of Noxious Metallic Ions in Wastewater,” Korean Journal of Economic and Environment Geology, Vol. 28, No. 3, 1995, pp. 231-241.
- Y. Doi, T. Shibutani, Y. Moriwaki, T. Kajimoto and Y. Iwayama, “Sintered Carbonate Apatites as Bioresorbable Bone Substitutes,” Journal of Biomedical Research, Vol. 39, 1998, pp. 603-610. doi:10.1002/(SICI)1097-4636(19980315)39:4<603::AID-JBM15>3.0.CO;2-7
Nomenclature
B—Langmuir constant;
C—Concentration in the fluid phase, mol/m3;
k—Freundlich constant, mol/kg;
m—Number of component;
n—Exponent;
N—Number of data points;
q—Amount adsorbed, mol/kg;
qT—Total adsorbed amount, mol/kg;
qm—Amount adsorbed for monolayer formation, mol/kg;
R—Gas constant, J/mol·K;
T—Temperature, K;
Z—Mole fraction in the adsorbed phase;
π—Spreading pressure.

