Circuits and Systems
Vol.5 No.3(2014), Article ID:44140,11 pages DOI:10.4236/cs.2014.53008
DAPSO and PSO-VAF in Linear Phase Digital Low Pass FIR Filter Design
Mudit Shukla, G. R. Mishra
Department of Electronics & Communication Engineering, Amity University Uttar Pradesh, Lucknow, India
Email: mudit.shuklaec@gmail.com, grmishra@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 4 January 2014; revised 4 February 2014; accepted 14 February 2014
ABSTRACT
Digital filters play a key role in the field of digital signal processing. This paper presents a linear phase digital low pass finite impulse response (FIR) filter design using particle swarm optimization and its two new variants, dynamic and adjustable particle swarm optimization (DAPSO) and particle swarm optimization with variable acceleration factor (PSO-VAF) and illustrates the superiority of the PSO-VAF method over PSO based methods. Two fitness functions are considered. The fitness1 is used to find the possible minimum ripples in pass band and stop band in case of PSO, DAPSO and PSO-VAF. Fitness2 is able to control the ripples in both bands separately. A comparison of simulation results demonstrates the performance of PSO and its methods in designing digital low pass FIR filters.
Keywords:Digital Filters Design; Low Pass FIR Filters; PSO; DAPSO; PSO-VAF

1. Introduction
In the modern age, digital signal processing (DSP) is the indispensable part of the human life, due to its numerous applications such as telecommunication, speech processing, consumer electronics systems, biomedical systems, image processing, military and defense electronics systems, aerospace and automotive electronics systems and industrial applications [1] . DSP has two major classes of systems. The first system is used to perform signal filtering in time domain and known as digital filter. The second system gives signal representation in frequency domain and known as spectrum analyzer. Digital filters are the most essential element of the DSP and classified into two types, finite impulse response (FIR) and infinite impulse response (IIR). FIR filters or non-recursive filters are those for which the output of the filter depends only on the present input. FIR filters are widely used due to its advantages like it is inherently stable since the poles lie within the unit circle and can be designed as linear phase filters, making them a better choice in phase sensitive application [2] .
There are many different techniques available for the design of digital filters, such as window methods, frequency sampling methods and Parks-McClellan equiripple algorithm. The simplest and most popular way to design FIR filter is by windowing. In this method, ideal impulse response is multiplied with different window functions, such as Butterworth, Chebyshev, Kaiser and Hamming etc., depending on the requirements of ripples on the pass and stop band, stop band attenuation and transition width. But this method does not allow controlling the approximation errors in different bands. In frequency sampling method, any kind of frequency response can be approximated. But in this method, there is no direct formula to calculate the filter order [3] . Parks-McClellan (PM) method based on Remez Exchange algorithm provides an optimum equiripple approximation to the desired frequency response. But in this method, the relative values of the amplitude error in the frequency bands are specified by weighting function and not by deviations themselves [4] . In these methods, designer always has to compromise on one or more of the design specifications.
The intelligent optimization techniques have been successfully implemented in the design of digital filters and provide better parameter control as well as better approximate the ideal filter. Simulated annealing, Tabu search, Differential evolution and artificial bee colony algorithm are some intelligent optimization techniques, which have proved their capability of designing digital filters. Simulated annealing (SA) was used to design linear phase digital filter, Nyquist filter and cascade form FIR filter. However, in this approach computation time is quite long (especially for higher order filter) and does not guarantee finding the global optimum [5] . The tabu search was applied to design approximation problem of FIR digital filter with quantized coefficients using a flexible realization of the filter taps, which allows getting higher accuracy [6] . Another population based algorithm, differential evolution (DE), was applied to design with different order FIR filter. However, this approach is computationally less expensive than Genetic algorithm [7] . A new design method based on artificial bee colony algorithm (ABC) was used to design IIR filters [8] .
The particle swarm optimization (PSO) is population based intelligent optimization technique that has proven to be effective in multidimensional nonlinear environment; all of the constraints of filter design can be effectively taken care of by the use of PSO. PSO and its several modifications have been successfully implemented in digital filter designing problems [9] -[14] . In this paper, we propose two new variants of PSO for designing linear phase low pass FIR (LP FIR) filter.
2. FIR Filter Design Issues
The transfer function of FIR digital filter is given by
 (1)
(1)
And the frequency response of FIR digital filter is given by
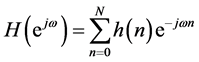 (2)
(2)
In this paper we design an even order, odd length and even symmetry low pass FIR filter. For this the symmetry condition is given as
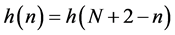 (3)
(3)
where N is the order of the filter and from (3) it is clear that the number of coefficients is to be optimized (N/2 + 1). The main objective of FIR filter design is to find the filter coefficients in optimized way that results in optimum filter. The filter is optimum, when maximum weighted error is minimized. In the PM algorithm [15] , an approximate error function is defined by
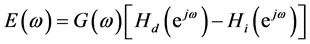 (4)
(4)
where 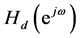 and
and  are the frequency responses of the designed approximate filter and ideal filter respectively. The weighting function,
are the frequency responses of the designed approximate filter and ideal filter respectively. The weighting function, 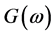 , is used to provide the approximation error differently in different frequency bands. For an ideal LP filter,
, is used to provide the approximation error differently in different frequency bands. For an ideal LP filter, 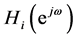 is defined as
is defined as
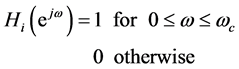 (5)
(5)
where 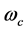 is the cutoff frequency. In this paper we consider two fitness functions for designing LP FIR Filter [16] . The first fitness function is used to design optimum filter, means finding the possible minimum ripples in both, pass band
is the cutoff frequency. In this paper we consider two fitness functions for designing LP FIR Filter [16] . The first fitness function is used to design optimum filter, means finding the possible minimum ripples in both, pass band 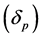 and stop band
and stop band . This fitness function is given as
. This fitness function is given as
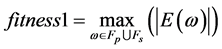 (6)
(6)
where Fp and Fs are the closed subsets 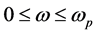 and
and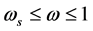 , respectively. The other fitness function is used to control the ripples in pass band and stop band separately, and is given as
, respectively. The other fitness function is used to control the ripples in pass band and stop band separately, and is given as
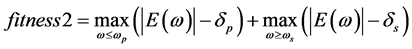 (7)
(7)
where  and
and  are the pass band and stop band normalized cutoff frequencies.
are the pass band and stop band normalized cutoff frequencies.
3. Intelligent Optimization Techniques
3.1. Particle Swarm Optimization (PSO)
PSO is inspired by the observation of social behavior of bird flocking and fish schooling. This powerful global optimization technique was first found by Kennedy (a social psychologist) and Eberhart (an electrical engineer) in 1995 [17] . PSO is simple, fast, requires less storage and can be coded in few lines. In PSO every particle remembers its best solution  as well as the group’s best solution
as well as the group’s best solution . It means that PSO have good memory. The PSO is worked on the concept of “constructive cooperation” between particles, so that it is easily able to solve multidimensional optimization problems. In PSO global optimum is achieved by an iterative procedure. The PSO technique is based on the five basic principles of the swarm intelligence [18] . These are, Proximity, i.e., the swarm must be able to perform simple space and time computations. Quality, i.e., the swarm should be able to respond to quality factors in the environment. Diverse response, i.e., the swarm should not commit its activities along excessively narrow channels. Stability, i.e., the swarm should not change its behavior every time the environment changes. Adaptability, i.e., the swarm must be able to change its behavior, when the computation cost is affordable.
. It means that PSO have good memory. The PSO is worked on the concept of “constructive cooperation” between particles, so that it is easily able to solve multidimensional optimization problems. In PSO global optimum is achieved by an iterative procedure. The PSO technique is based on the five basic principles of the swarm intelligence [18] . These are, Proximity, i.e., the swarm must be able to perform simple space and time computations. Quality, i.e., the swarm should be able to respond to quality factors in the environment. Diverse response, i.e., the swarm should not commit its activities along excessively narrow channels. Stability, i.e., the swarm should not change its behavior every time the environment changes. Adaptability, i.e., the swarm must be able to change its behavior, when the computation cost is affordable.
PSO starts with a population of random particles (potential solution) in a D-dimension space. A position ‘X’ and velocity ‘V’ are associated with each particle. The position and velocity of the  particle are given as
particle are given as
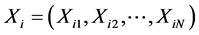 (8)
(8)
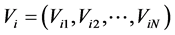 (9)
(9)
The velocity and position are updated according to the formula given as
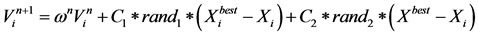
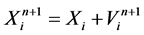 (11)
(11)
where  and
and 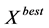 is the individual best and global best positions respectively,
is the individual best and global best positions respectively, 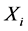 is the current position of the
is the current position of the  particle, n+1 and n denote the current and the previous iterations, rand1 and rand2 are random numbers in the range [0,1]. These random numbers are update every time they occur. C1 and C2 are the two positive constants, called cognitive and social acceleration factors respectively and
particle, n+1 and n denote the current and the previous iterations, rand1 and rand2 are random numbers in the range [0,1]. These random numbers are update every time they occur. C1 and C2 are the two positive constants, called cognitive and social acceleration factors respectively and 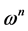 is the inertia weight in the
is the inertia weight in the 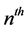 iteration. A linearly damped inertia weight is preferred for better convergence [19] .
iteration. A linearly damped inertia weight is preferred for better convergence [19] .
The PSO algorithm for filter designing is as follows:
1) Define the filter specifications, fitness function, and population size and set the boundaries, i.e. maximum and minimum value of coefficient.
2) Initialize a population array of particles with random positions and velocities in the problem space.
3) For each particle, Compare particle’s fitness evaluation with its 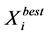 and
and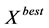 . If fitness(x) better than fitness
. If fitness(x) better than fitness 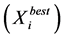 then
then  (current value) and if fitness(x) better than fitness
(current value) and if fitness(x) better than fitness 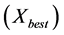 then
then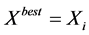 .
.
4) Update the velocity according to (10) and Move each particle to new position according to (11).
5) Loop from 2 - 4 until stopping criterion is satisfied.
6) Output is the coefficient of the desired filter (N/2 + 1).
3.2. Dynamic and Adjustable Particle Swarm Optimization (DAPSO)
In order to improve the performance of PSO and maintain the diversities of the particles, a novel algorithm called Dynamic and Adjustable Particle Swarm Optimization (DAPSO) is proposed [20] . The distance from each particle to the  position is calculated in order to adjust the velocity suitably of each particle by using following function
position is calculated in order to adjust the velocity suitably of each particle by using following function
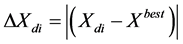 (12)
(12)
 (13)
(13)
where 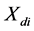 is the position of
is the position of 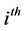 particle, and
particle, and 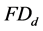 is the furthest distance from the particle to
is the furthest distance from the particle to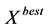 .
.
This algorithm follows the same steps as PSO but a little change at step 4. In this algorithm velocity is updated according to the formula given as
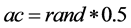 (14)
(14)
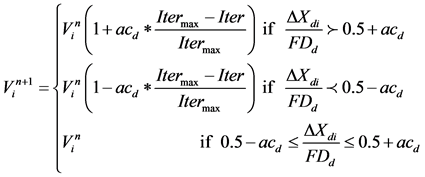
Then this new velocity value put into (11) and updates the position. Finally it gives the desired filter coefficients.
3.3. Particle Swarm Optimization with Variable Acceleration Factor (PSO-VAF)
A novel PSO with variable acceleration factor (PSO-VAF) has been proposed [21] . In this algorithm a modification has been made with C1 and C2, acceleration factors appears in (10). C1 has been allowed to decrease from its initial value of C1i to C1f while C2 has been increased from C2i to C2f using the following equation
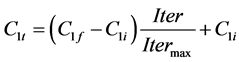 (16)
(16)
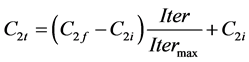 (17)
(17)
Then in this case velocity update formula is given by
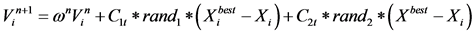
The rest of the algorithm follows the same steps as given in PSO.
4. Design Examples and Discussion
In this section, we demonstrate the use of the PSO, DAPSO and PSO-VAF to design a 20 order low pass FIR fitter. All the simulation results shown in this paper, has been made on MATLAB 7.10. The specifications of the filter to be designed using these algorithms are: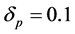 ,
, 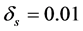 ,
,  and
and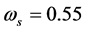 . Table 1 shows the parameters and its corresponding value consider during this work.
. Table 1 shows the parameters and its corresponding value consider during this work.
Figure 1 shows the frequency response in dB of the LP FIR filter designed using PSO, DAPSO, and PSOVAF in the case of fitness1. On the same plot, the same filter designed using the PM is also shown. The main purpose behind using the fitness1 is to find the possible minimum ripples in pass band and stop band in case of PSO, DAPSO and PSO-VAF. Figure 2 shows the frequency response in dB of the LP FIR filter in the case of fitness2. Fitness2 is able to control the ripples in both bands separately. Table 2 and Table 3 show the optimized coefficients of LP FIR using fitness1 and fitness2, respectively. Figure 3 shows the normalized plot of LP FIR using fitness2. Figure 4 and Figure 5 shows the normalized plot of pass band and stop band ripples, respectively in case of fitness2. The simulation results for fitness2 shows that PSO gives 30.90dB stop band attenuation and DAPSO gives 32.32dB stop band attenuation. PSO-VAF results in 33.07dB stop band attenuation. Hence result quality is improved as indicated in Table 4.
4.1. Convergence of PSO, DAPSO and PSO-VAF
Figures 6-8 shows the convergence behavior of PSO, DAPSO and PSO-VAF respectively. These plots provide the error fitness value of the algorithms with number of iterations. PSO converges to the minimum error fitness value of 0.9392 in 55.39 sec. DAPSO converges to the minimum error fitness value of 1.129 in 35.92 sec. PSOVAF converges to very low error fitness value of 0.0581 in 17.38 sec. PSO-VAF converges very fast as compare to the PSO and DAPSO in finding the desired filter coefficients.
Table 1. PSO, DAPSO, PSO-VAF Parameters.
Table 2. Optimized Coefficient of LP FIR using Fitness1.

Figure 1. Frequency Response of LP FIR using Fitness 1.

Figure 2. Frequency Response of LP FIR using Fitness 2.
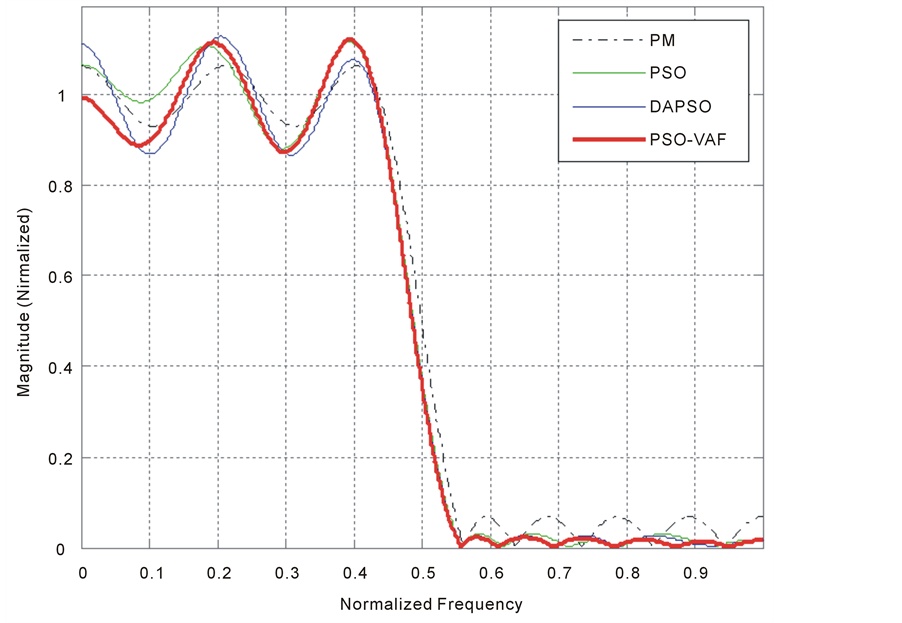
Figure 3. Normalized Plot of LP FIR using fitness 2.
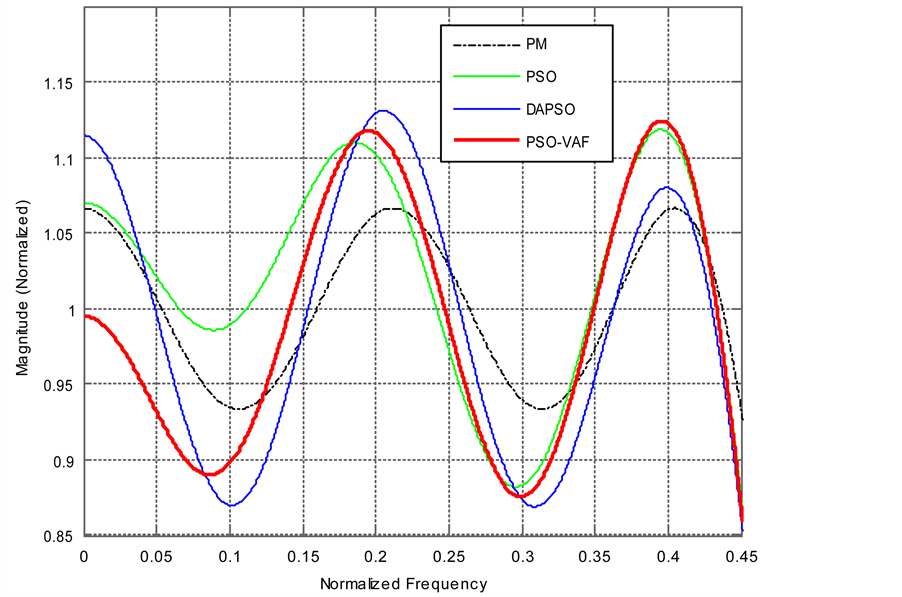
Figure 4. Normalized Pass Band ripples using fitness 2.

Figure 5. Normalized Stop Band ripples using fitness 2.
Figure 6. Convergence plot for PSO using fitness2.
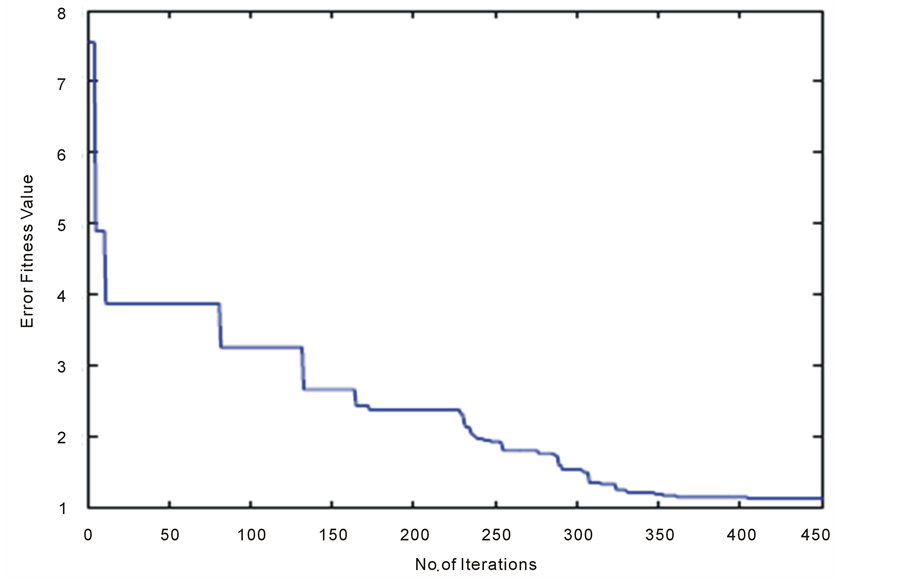
Figure 7. Convergence plot for DAPSO using fitness 2.
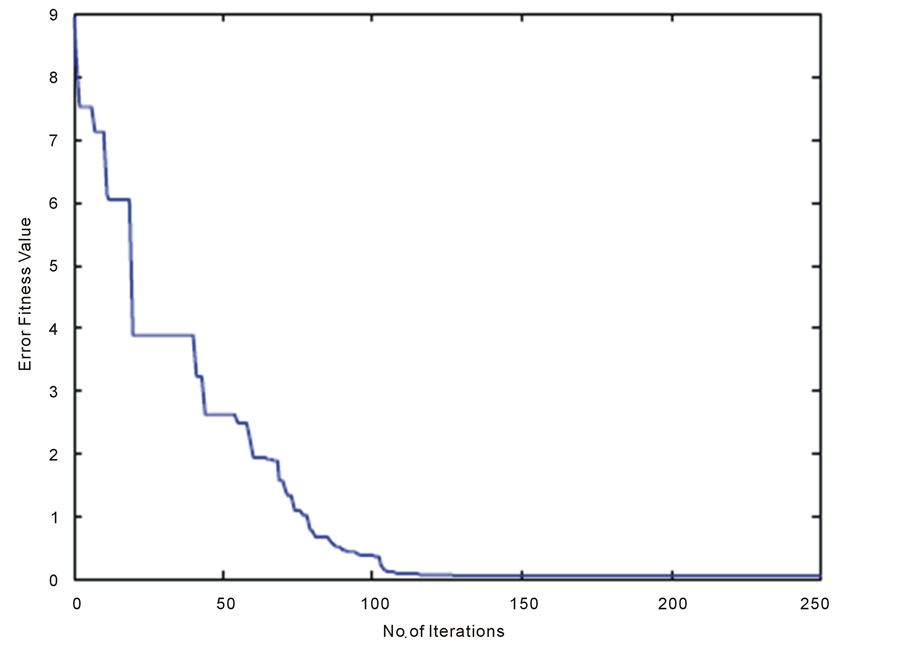
Figure 8. Convergence plot for PSO-VAF using fitness2.
Table 3. Optimized Coefficient of LP FIR using Fitness 2.
Table 4. Results statistics.
5. Conclusion
In this paper, the application of PSO and its two new variants, DAPSO and PSO-VAF, to design linear phase low pass FIR filter, have been carried out. Comparison of results of PM, PSO, DAPSO and PSO-VAF has been made. It is analyzed that the performance of DAPSO is better than PSO in context of stop band attenuation. On the other hand, PSO-VAF provides better stop band attenuation as compared to both, PSO and DAPSO. The convergence behavior of the algorithms is also compared and it is examined that PSO-VAF quickly converge with very low error fitness value. Two fitness functions are considered. The obtained results show that fitness2 is the better choice for designing optimal digital low pass FIR filter.
References
- Shenoi, B.A. (2006) Introduction to Digital Signal Processing and Filter Design. John Wiley & Sons, Inc., Hoboken.
- Oppenheim, A.V., Schafer, R.W. and Buck, J.R. (1999) Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs.
- Proakis, J.G. and Manolakis, D.G. (2007) Digital Signal Processing: Principles, Algorithms, and Applications. 4th Edition, Pearson Education, Inc., New Delhi.
- Parks, T.W. and McClellan, J.H. (1972) A Program for the Design of Linear Phase Finite Impulse Response Filters. IEEE Transactions on Audio and Electroacoustics, 20, 195-199. http://dx.doi.org/10.1109/TAU.1972.1162381
- Benvenuto, N., Marchesi, M. and Uncini, A. (1992) Applications of Simulated Annealing for the Design of Special Digital Filters. IEEE Transactions on Signal Processing, 40, 323-332. http://dx.doi.org/10.1109/78.124942
- Traferro, S., Capparelli, F., Piazza, F. and Uncini, A. (1999) Efficient Allocation of Power of Two Terms in FIR Digital Filter Design Using Tabu Search. Proceedings of the 1999 IEEE International Symposium on Circuits and Systems, Orlando, 30 May 1999-2 Jun 1999, 411-414.
- Nurhan, K. and Cetinkaya, B. (2006) Design of Digital FIR Filters Using Differential Evolution Algorithm. Circuits, Systems and Signal Processing, 25, 649-660. http://dx.doi.org/10.1007/s00034-005-0721-7
- Nurhan, K. (2009) A New Design Method Based on Artificial Bee Colony Algorithm for Digital IIR Filters. Journal of the Franklin Institute, 346, 328-348. http://dx.doi.org/10.1016/j.jfranklin.2008.11.003
- Mondal, S., Ghoshal, S.P., Kar, R. and Mandal, D. (2012) Novel Particle Swarm Optimization for Low Pass FIR Filter Design. 2012 IEEE Symposium on Humanities, Science and Engineering Research (SHUSER), Kuala Lumpur, 24-27 June 2012, 413-418.
- Mukherjee, S., Kar, R., Mandal, D., Mondal, S. and Ghoshal, S.P. (2011) Linear Phase Low Pass FIR Filter Design Using Improved Particle Swarm Optimization. 2011 IEEE Student Conference on Research and Development (SCOReD), Cyberjaya, 19-20 December 2011, 358-363.
- Archana, S., Mahapatra, R.K. and Panigrahi, S.P. (2011) DEPSO and PSO-QI in Digital Filter Design. Expert Systems with Applications, 38, 10966-10973. http://dx.doi.org/10.1016/j.eswa.2011.02.140
- Zhao, Z.K. and Gao, H.Y. (2009) FIR Digital Filters Based on Cultural Particle Swarm Optimization. Proceedings of 2009 International Workshop on Iriformation Security and Application (IWISA 2009), Qingdao, 21-22 November 2009, 252-255.
- Meisam, N. and Ayatollahi, A. (2008) A Comparison between Genetic Algorithm and PSO for Linear Phase FIR Digital Filter Design. 9th International Conference on Signal Processing, Beijing, 26-29 October 2008, 2134-2137.
- Luitel, B. and Venayagamoorthy, G.K. (2008) Particle Swarm Optimization with Quantum Infusion for the Design of Digital Filters. IEEE Swarm Intelligence Symposium, St. Louis, 21-23 September 2008, 1-8.
- Parks, T.W. and McClellan, J.H. (1972) Chebyshev Approximation for Non Recursive Digital Filters with Linear Phase. IEEE Transactions on Circuits Theory, 19, 189-194. http://dx.doi.org/1109/TCT.1972.1083419
- Ababneh, J.I. and Bataineh, M.H. (2008) Linear Phase FIR Filter Design Using Particle Swarm Optimization and Genetic Algorithms. Digital Signal Processing, 18, 657-668. http://dx.doi.org/10.1016/j.dsp.2007.05.011
- Kennedy, J. and Eberhart, R.C. (1995) Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks, Perth, 27 November 1995-1 December 1995, 1942-1948. http://dx.doi.org/10.1109/ICNN.1995.488968
- Kennedy, J. and Eberhart, R.C. (2001) Swarm Intelligence. Morgan Kaufmann, San Francisco.
- Robinson, J. and Rahmat-Samii, Y. (2004) Particle Swarm Optimization in Electromagnetics. IEEE Transactions on Antennas and Propagation, 52, 397-402. http://dx.doi.org/10.1109/TAP.2004.823969
- Liao, C.-Y., Lee, W.-P., Chen, X.H. and Chiang, C.-W. (2007) Dynamic and Adjustable Particle Swarm Optimization. Proceedings of the 8th WSEAS International Conference on Evolutionary Computing, Vancouver, 23-25 September 2008, 301-306.
- Tripathi, P.K., Bandyopadhyay, S. and Kumar Pal, S. (2007) Multi Objective Particle Swarm Optimization with Time Variant Inertia and Acceleration Coefficients. Information Sciences, 177, 5033-5049. http://dx.doi.org/10.1016/j.ins.2007.06.018.


