ABSTRACT

The Born-rule, which assigns probabilities to measurement outcomes, is one of the fundamental axioms of quantum physics. It dates back to the time of the establishment of the formalism of quantum physics in the first half of the 20^th century. From the beginning, and particularly in connection with the development of different interpretations of the theory, there has been a desire/need to better understand the true nature of the Born-probabilities. Are they classical/epistemic of origin or are they irreducible and of on tic stature as a kind of intrinsic propensities of physical systems? We show that, by only using the mathematical formalism of the original theory, we find a possible answer.

Keywords:

Quantum Measurement, Quantum Ontology, Density Operator

1. Introduction

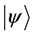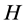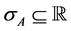The formalism of quantum physics has been developed during the first decades of the 20^th century. It describes a physical system as an element of some appropriate Hilbert space and physical, observable quantities as eigenvalues in the spectrum of self-adjoint operators 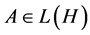on that Hilbert space. The eigenvalue-eigenstate postulate says that, whenever a system is found to have a value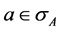, then it is in the corresponding eigenstate 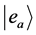of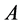. Inversely, if a system 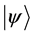is represented in the eigenbasis, 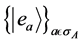, of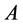, , then the system is experimentally found to have eigenvalue 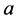with probability

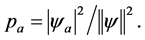(1)

This is the Born-rule [1] . The Born-rule together with the eigenvalue-eigens- tate link constitutes the measurement postulate. No violation of the Born-rule has ever been discovered experimentally. The measurement postulate is incompatible with a further postulate of quantum mechanics, namely the unitary evolution of the quantum state. Ever since the establishment of the theory there have been different interpretations and extensions of quantum physics in order to solve this incompatibility, known as the “measurement problem”.

There are some questions, which naturally arise with regard to the Born-rule. Firstly, why are there probabilities in the first place and secondly, what kind of probabilities are they? Both questions are intimately linked to interpretations of quantum mechanics and have in this context found various answers. Focusing on the second question we find the opinions, starting on the realist side, that the probabilities might be objective, irreducible properties of quantum systems, as in the GRW interpretations [2] or, passing to the epistemic/instrumentalist side, subjective degrees of belief [3] or, yet represent something else, like rational preferences in the decision-theoretic explanations of the many-worlds interpretation [4] [5] [6] [7] . Because the formalism of quantum physics shows the kind of ontological under determination it does, the Born-rule does as well. In this paper we follow the original, basic formalism and will give a possible answer to the question of the nature of the probabilities.

2. Some Formalism

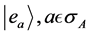Given the resolution of a state in the eigenbasis, of an operator, , we can form the corresponding density matrix with matrix-entries. This matrix is a self-adjoint operator, a projection operator in this case, satisfying. If is normalized, , then so is the trace of, , and the diagonal matrix-elements of happen to correspond to the numerical values in the Born probabilities. By the correspondence, , there is an alternative formulation of the postulates of traditional quantum physics in terms of density operators. If a density operator satisfies, i.e. is a projector, we say that is pure. Density operators can be thought to incorporate the known information about a state and this allows a generalization. Given a set of pure density operators and a set of probability weights, , we can form a new density operator

(2)

We say that the operator in (2) is a mixed state. Mixed states are formally self-adjoint operators with but no projectors, so. The interpretation of mixed states is entirely classical in the sense that the probabilities reflect a lack of knowledge and hence belief in the likelihood of elements of a set of possible preparations, done in a lab for instance. There is a theorem due to Gleason [8] , which basically says that the trace-function

is the unique probability measure, which is faithful to the postulates of quantum physics on Hilbert space¹. Gleason’s theorem tells us that we are looking at the right probabilities. But it is per se not helpful to better understand the nature of the Born-probabilities.

Measurement

Assume there is a density matrix and basis (eigen)-states, corresponding to some self-adjoint operator. Assume in addition that there is an additional system with orthonormal basis states, which we assume originally to be in the base state. A measurement of by the probe is an operation on the joint system

(3)

where is unitary ². A general unitary transformation on a tensor-product, expressed in the respective bases, can be written as a matrix

(4)

where the operators are given by. We denote the diagonal sub-block simply by. Since is unitary, we have

(5)

Conversely, we can choose any set of operators satisfying the resolution of the identity-condition (5) to define a measurement on an initial joint state. We now have the necessary elements in place to give the main argument.

3. The Born-Rule

Assume there is a quantum system in a, not necessarily normalized, pure state with representation, and corresponding density matrix with matrix elements

. We further assume all the postulates of traditional quantum physics as above, except the Born-rule, and ask ourselves where the probabilities come from.

Assume there is a second system with basis and an observer who would like to know in what state the system is in, by making an appropriate measurement on the joint system. If that is possible in the first place, then, having no additional knowledge, the observer does a priori not know in what state, the probe will be after the measurement and before observation.

³. The probe can be chosen appropriately coarse- grained⁴ such that We now introduce probabilities by Laplace’s principle of indifference. The observer is after the measurement and before observation in a situation where, by lack of further information, she will a priori attribute to each outcome equal probability

. This attribution is equivalent to maximizing the entropy function. The observer can therefore write down in the spirit of (2) an average of outcomes

(6)

For our purpose we now chose the operators to be the scaled projectors to the basis-states. Note that we have replaced the simple-index by the double-index. This choice is consistent with the demands of a measurement, since the satisfy (5)

(7)

Therefore we can write (6) in the following form

(8)

Comparing Equation (8) with Equation (2), we see that can be viewed as a mixed state with probabilities

(9)

which is the Born-rule.

4. Conclusions

We have in the above derivation not made use of any specific interpretation of quantum mechanics, but relied on two basic assumptions only. The first one is the formalism of density operators and generalized measurement with classical or epistemic probabilities arising in mixed states (2). The second one is Laplace’s principle of indifference in order to introduce the concept of probabilities and to assign concrete probability-values, to the mixed state in (6). This is the important step, which helps to avoid the kind of tautological argument based on the reduced density matrix and Gleason’s theorem. It bases on a kind of symmetry of the probe states, due to a lack of knowledge before observation.

We have found that, given any not necessarily normalized pure state, it is possible to define an observer with an appropriately coarse-grained probe-system⁵ who, by lack of further knowledge, will assign exactly the Born-probabilities, as classical probabilities in the sense of (2), to finding the system in one of the basis-states, after the measurement and before observation. In other words, there is the possibility to interpret the normalized amplitudes of an arbitrary state as epistemic probabilities for different possible measurement outcomes.

If a quantum state is given to us a priori, then it seems that the Born- probabilities are objectively given with it and there might be a reluctance to embrace Laplace’s principle as fundamental [9] . It seems to us that we can accept the principle as deeply rooted in our intuition and therefore to be a first principle. Authors, concerned with the many worlds interpretation in [6] [7] for instance, try to give more objective physical justifications for Laplace’s principle, mainly by describing the symmetry, which it bases on, in more physical terms. We are not sure that these ideas are really more fundamental or whether they are not the same intuition vested in different garments. We should in all this always remember that quantum states are practically given to us by making preparations, i.e. by correlating them with other systems in laboratories. It is a wonderful fact, however, that the Born-probabilities are confirmed by the corresponding frequencies, if repeated experiments are being done. This would probably not be further impressive, if quantum states would just be results of gathering measurement information. But they can also arise from an initial state by Schrödinger evolution. We at least can say that nature seems to “play the game”.

Cite this paper

Schlatter, A. (2017) On the Nature of the Born Probabilities. Journal of Modern Physics, 8, 756- 760. https://doi.org/10.4236/jmp.2017.85047

References

NOTES

¹Under condition that the dimension of the Hilbert space is at least three.

²This follows from the fact that a general interaction evolution is unitary.

³Since the rational numbers are dense in, the choice of is general enough.

⁴This coarse-graining is used first by [6] and then by [7] in the context of many-worlds.

Let the underlying pure state have coefficients

⁵The environment could serve as a probe-system for instance.