Journal of Modern Physics
Vol.08 No.03(2017), Article ID:74437,8 pages
10.4236/jmp.2017.83020
Bio-Soliton Condensation in Human Body
Qiao Bi
Department of Physics, Science School, Wuhan University of Technology, Wuhan, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 3, 2017; Accepted: February 25, 2017; Published: February 28, 2017
ABSTRACT
In this work, we try to build a model to describe the condensation through the couple of bio-solitons in a well based on the BCS theory extended by the nonlinear operator, which can be used to simulate the created process of the internal elixir in the middle of the abdomen of the human body. The goal of this work is to provide a mechanism to explain the effect of stored bio-energy in the bio-systems.
Keywords:
Bio-Soliton, Condensation, Nonlinear Oscillation

1. Introduction
The Davydov soliton is a fundamental nonlinear excitation in the bio-system of human being, which has been discovered by the Davydov in 1973 [1] [2] [3] . By improving his model, Pan Xiao-feng presented that the Davydov soliton is the basic transformed unit of energy and information in bio-system included human body [4] [5] . Many facts also reveal that the bio-solitons sometimes can be seen as electrically longitudinal vibrations travelling along proteins, microtubules and DNA, etc., including interfering with local resonant oscillations by excitation of neighboring molecules and macromolecules [6] , for example, C. W. Smith presented a model of ideal cell resonance [7] and Fröhlich presented the coherent oscillation of bio-system in 1978 [8] [9] , etc. However, is it possible that this kind of oscillation as a macro-quantum condensation can take place in our body? This problem is interesting because many theories of acupuncture (even including Qigong and Yoga) believe that the down Dan Tian, i.e. about the middle of the abdomen of the human body, is an important accupoint to store bio-energy, until an internal elixir appears [10] . For a long time the internal elixir is an imaginary matter with unclear physical meaning but still pursued by the thousands and thousands practicers, therefore studying this problem is significant for the investigation of mechanism of acupunctures and relative points for helping innumerable practicers.
So, in previous works we have presented that the Davydov solitons can condense in two or three potential wells for simulating the oscillation of quasiparticles in the accupoints [11] [12] . In this work, we try to further explore the relative micro-mechanism, namely the condensation through many couple of bio-solitons in a well based on the BCS (Bardeen―Cooper―Schrieffer) super- conductor theory extended by the nonlinear operator [13] [14] . Then this model can be used to simulate the creation of internal elixir in the middle of the abdomen of the human body. The meaning of this model is that it provides a mechanism to explain the micro-process of stored bio-energy in our body [15] .
2. Bio-Physical Model
The nonlinear excitations (solitons) are supposed to have a condensation in a well of the belly. This assumption is based on the Chinese medicine theories and Acupuncture theories, and also from the results of the thousands and thousands practicers of Qigong or Yoga over thousands years of the world [10] [15] . Then from mathematical and physical points of view we can find the conditions: 1) If the interactions between the solitons all have the same frequency of vibration; 2) If they all have the same moment (or opposite moment), then it can be proven that the numbers of solitons which take place interaction are more possible than other cases. So for simplicity, we consider a physical model describe this sort of condensation process, i.e. the two solitons with opposite moments are condensed into a couple of solitons by exchanging an imaginary phonon (or phonon soliton). In this case the Hamiltonian can be written by
 (1)
(1)
where  is defined as a coupling number for a couple of solitons, which is constant;
is defined as a coupling number for a couple of solitons, which is constant;  is a wave vector of a soliton,
is a wave vector of a soliton,
 (2)
(2)
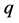 is a wave vector of a (solitonic) phonon, and
is a wave vector of a (solitonic) phonon, and 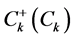 is a creation (annihilation) operator of a soliton with
is a creation (annihilation) operator of a soliton with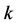 , respectively. Here the quasiparticle is defined as a soliton or a nonlinear excitation generally. So the interaction part of the Hamiltonian can be written as
, respectively. Here the quasiparticle is defined as a soliton or a nonlinear excitation generally. So the interaction part of the Hamiltonian can be written as
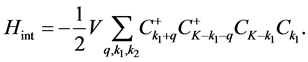 (3)
(3)
Then we can find when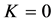 , the numbers of the solitons participating scattering process is more larger than other situations, hence the above
, the numbers of the solitons participating scattering process is more larger than other situations, hence the above 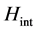 can be written approximately by
can be written approximately by
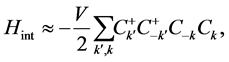 (4)
(4)
where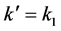 .
.
Therefore, by adding the terms of the energy part for the soliton, the total Hamiltonian can be expressed as
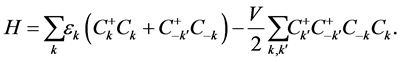 (5)
(5)
3. Diagonalization of Hamiltonian
The Hamiltonian 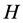 can be firstly simplified by using following forms
can be firstly simplified by using following forms
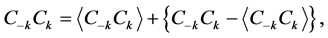 (6)
(6)
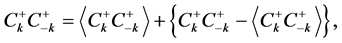 (7)
(7)
and supposing the difference of these operators of the couple of solitons is small value; we therefore can replace the above Equations (6) and (7) into
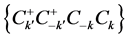 and take 1-order of approximation, so the Hamiltonian
and take 1-order of approximation, so the Hamiltonian 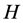 is changed as
is changed as

where we have used

Now, by defining

the 

where notice

By applying the Heisenberg equation, we get an equation for



For solving these two equations the so-called Bogoliubov transformation is applied,


where denote that 




and

For example, for the nonlinear operator


Then all properties of the linear operator can be applicable to the

So, Equations (15) and (16) can be inverted as


by replacing Equations (21) and (22) into the Hamiltonian (11), we get

where notice again that the Slach product has been introduced. So if let the off-diagnal term in 

then by use Equations (20) and (24) we can obtain

where

and

Hence, we have


These allow us to obtain the diagnalized Hamiltonian as

where the energy of basic state is expressed by

and the excitation energy is

so 


4. The Calculation of
When the system arrives at the lowest condensation temperature 

then we get

and

where denote

By considering Equations (28) and (29) replaced into Equation (36) to cancel

finally we can get

and

where 

for bio-solitons condensation in our body the temperature 

where the bio-system can regulate the







5. Big Soliton
Furthermore if we assume that 

then


then since 

and 



where defining

Then in the situation of no external field condition, which is just a suitable condition for the oscillation inside of the belly, we have the density of the free energy expressed as

then applying the principle of minium of the free energy we get

which allows us to have

This is just a kind of Ginzburg and Landau equation which can describe a soliton. For example in the three dimensional case we can have

where defining

Then the solution of Equation (48) can be gotten by

where notice 

This 
6. Conclusion
A couple of bio-solitons condensation has been presented. The two solitons with opposite moments are condensed into a couple of solitons by exchanging imaginary phonons. Then these couple of solitons can form a big soliton with oscillation. The process can be taken place in the room temperature, and the higher temperature makes the realization easier than lower temperature. This model can be used to simulate the bio-energy stored in our body such as the middle of abdomen of the human body, and also provides a kind explanation of mechanism for the internal elixir formation. This means that the so called internal elixir may be formed through the macro-quantum condensation of a couple of solions, and then the condensation plays a sort of oscillation as a big (or macro-) soliton.
Cite this paper
Bi, Q. (2017) Bio- Soliton Condensation in Human Body. Journal of Modern Physics, 8, 315-322. https://doi.org/10.4236/jmp.2017.83020
References
- 1. Davydov, A.S. (1979) Physica Scripta, 20, 387-396.
https://doi.org/10.1088/0031-8949/20/3-4/013 - 2. Davydov, A.S. and Kislukha, N.I. (1973) Physica Status Solidi (b), 59, 465-470.
https://doi.org/10.1002/pssb.2220590212 - 3. Davydov, A.S. (1973) Journal of Theoretical Biology, 38, 559-569.
https://doi.org/10.1016/0022-5193(73)90256-7 - 4. Pang, X.F. and Feng, Y.-P. (2005) Quantum Mechanics in Nonlinear Systems. World Scientific Publishing Co. Pte. Ltd., Singapore City.
https://doi.org/10.1142/5721 - 5. Pang, X.-F. (2000) Physical Review E, 62, 6989-6998.
https://doi.org/10.1103/PhysRevE.62.6516 - 6. Geesink J.H. and Meijer D.K.F. (2016) Bio-Soliton Model That Predicts Non-Thermal Electromagnetic Radiation Frequency Bands, That Either Stabilize or Destabilize Life Conditions. Bio. phys., arXiv:1610.04855.
- 7. Smith, C.W. and Best, S. (1989) Electromagnetic Man. J. M. Dent Ltd., London.
- 8. Fröhlich, H. (1988) Biological Coherence and Response to External Stimuli. Springer-Vering, Berlin.
https://doi.org/10.1007/978-3-642-73309-3 - 9. Fröhlich, H. (1982) Coherent Excitation in Biological System. Springer-Vering, Berlin.
- 10. Needham, J. (2015) Science and Civilisation in China. Vol. 5, Part 5, Chemistry and Chemical Technology, Cambridge University Press, London, New York.
- 11. Bi, Q. (2016) Information Soliton and Excitation from Nonlinearity. LAP LAMB-ERT Academic Publishing, Germany.
- 12. Bi, Q. (2016) Journal of Modern Physics, 7, 1811-1817.
https://doi.org/10.4236/jmp.2016.713161 - 13. Schwartz, C. (1997) Journal of Mathematical Physics, 38, 484-500.
https://doi.org/10.1063/1.531829 - 14. Schwartz, C. (1997) Journal of Mathematical Physics, 38, 38-41.
https://doi.org/10.1063/1.532070 - 15. Needham, J. (2011) Science and Civilisation in China. Vol. 5, Part 2, Chemistry and Chemical Technology, Cambridge University Press, London, New York.



