ABSTRACT

According to the Fowler theory and numerous experiments the quantum efficiency for photoemission from conductors increases with temperature. Here we show that an opposite temperature dependence is also possible, when the photoemission is from quasi-metallic surface accumulation layers of n-type semiconductors. This is due to the temperature dependence of the Fermi level energy in semiconductors. The Fermi level energy increases with decreasing temperature; this leads to a decrease of the semiconductor work function and consequently an increase of the quantum efficiency photoemission at constant value of absorbed light quanta of energy. We have calculated this effect for electron accumulation layer in n-GaN, induced by adsorption of positively charged cesium or barium ions. It is found that at low temperatures near liquid nitrogen, the quantum efficiency for photoemission increases to near 55%, which is comparable to the largest values, reported for any known photo-ca- thodes. This phenomenon may prove useful for efficient photo-cathodes operating at low temperatures.

Keywords:

Photoemission, Photocathode, Electronic Accumulation Layer, N-Type Semiconductor

1. Introduction

In 1931 Fowler developed a theory of photoelectron emission from metals using a simple Fermi-Dirac model for distribution of free electrons [1] [2] . The theory provided a simple and sufficiently accurate description of photoemission from metals, which still serves as a standard accepted model. In the model, electrons with high temperature, but below the level required to produce significant thermionic emission, emitted through the dominant thermally assisted photoemission process. Those electrons occupy states above the Fermi level, that enable photoemission induced by photons with energy 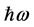below the photoemission threshold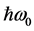. For 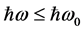the quantum efficiency (QE) spectral dependence is:

, (1)

at

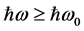
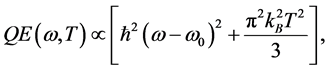(2)

where is the temperature, and 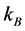is the Boltzmann’s constant. According to Eqs (1) and (2) the photoemission intensity increases with temperature, and this dependence is known as the conventional Fowler regime. Shortly after the publication of the Fowler theory, an experimental work by DuBridge et al. showed that the Fowler theory is not in complete quantitative agreement with experiment conducted for several metals [3] . The disagreement was observed for metals like molybdenum, niobium, zirconium and etc., in which the conductivity is not described by the free electrons model. 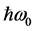However, in the cases where the photon energy is near threshold the model of Fowler-DuBridge, which does not take into account contribution of the band-effects, was found to be in a good agreement with experiment [3] .

Spicer et al. have continued to develop the theory, and in two seminal publications in 1958 and 1964, [4] [5] they proposed a three-step model, that took into account the excited electron momentum and Bragg reflections. In the first step of this model the incident photons are absorbed and excite electrons. The electrons then reach the solid surface of the solid undergoing electron-phonon and electron-electron scattering, and in the third step they escape to the vacuum through the surface barrier.

The free electron model may be satisfied not only for bulk metal but also for positively charged surface electron accumulation layer (AL) found in semiconductors. Such AL is formed at the positively charged surfaces of n-type semiconductors, when the conduction band edge at the surface is more than 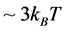below the Fermi energy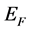. The AL can be induced by various factors such as high density of intrinsic cleavage defects on the free surface or donor-type surface states as well as by adsorbed alkali or rare-earth atoms. In such cases, a triangular shape potential well with a typical thickness of tens of nanometers and energy depth of up to ~1eV is formed in InN [6] . Due to the absence of quantization parallel to the surface, the electrons in such a well constitute a quasi-two dimensional metallic-like degenerated electron gas. Therefore, the electron concentration within the AL can be larger than the bulk concentration (as for example in InN) by 2 or 3 orders of magnitude and reach concentrations up to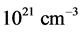, which is only around one order of magnitude lower the electrons concentration in metals [7] . In addition, it is known the photoemission intensity from quantum-well states in thin metallic films is considerably greater than the corresponding value of the bulk metal (see for example references [8] and [9] ). Therefore, it is not surprising that the photoelectron emission from the states of thin AL can make a significant contribution to the whole photoemission process.

Surface ALs were reported mainly for n-type narrow band gap semiconductors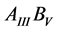, containing indium [7] [8] . However, in 2004 Benemanskaya et al. reported on the formation of surface ALs in n-GaN, induced by adsorption of sub-monolayers of positively charged cesium or barium ions [10] [11] [12] . It led to accumulation of electrons trapped in these 2D surface states. Analysis of these experiments suggests the existence of at least one filled band states at energy 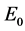below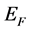, as shown schematically in Figure 2 in Ref. [11] .

In this work we analyze in details the photoelectron emission in the presence of surface electron accumulation layers in n-GaN. It is found that in such cases the electron emission possesses an opposite temperature dependence, which is due to the strong temperature dependence of the Fermi level energy in semiconductors. This phenomenon may be useful for increasing the photo emission from photo-cathodes operating at low temperatures.

2. Temperature Dependent Photoemission from Accumulation Layers in n-GaN

For clean n-GaN the photo-excitation threshold below 300 K lies in the near-ul- traviolet part of the spectrum in the wavelengths range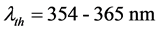, corresponding to the energy gap. In 2004 Benemanskaya et al found a sharp increase in photoemission from ALs n-GaN(0001) surface following adsorption of around half a monolayer of positive ions of cesium or barium [10] [11] [12] . The reported value of photoemission threshold from surface AL at room temperature, induced by cesium coverage with thickness of 0.5 ML is 1.4 eV, which corresponds to the infrared range with wavelength. The theory for photoemission from 2D metallic-like AL in semiconductor was considered in [10] [11] within the framework of the Urbakh-Brodsky theory for photoemission from metal surfaces [13] .

For calculating the photoemission we assume that the exciting light is S-polarized, where the square of matrix element of the optical transition is described by the following equation [12] :

(3)

Here is a half-width of the energy distribution of bulk states located around the Fermi level. The Fermi energy is measured from the vacuum level. In this case and therefore Equation (3) takes the form

(4)

From Eqs. (2) and (4) we extract the following expression for the spectral dependence of quantum efficiency photoemission from AL at:

(5)

The phenomenological constant C in Equation (5) can be obtained from photoemission measurements, if QE value is known for certain photon energy and temperature. However, the authors of Ref [10] [11] [12] do not report on the exact value of QE, but only report that the maximal QE of the Cs/n-GaN system is comparable and even exceeds the QE for highly- efficient source of electron GaAs photo-cathodes, which can reach 50% [14] . Therefore, we assume that the QE for the Cs/n-GaN system is also not less than 50% at room temperature for photon energy, which corresponds to the photoemission maximum, measured in Ref. [10] [11] [12] . Consequently, for ¹¹ and from Equation (5) we obtain the value of

We calculate below the temperature dependence of QE photoemission for surface AL of n-GaN for a photon energy corresponding to the intensity peak of the solar spectrum. The photoemission threshold energy at is assumed to be 1.4 eV. This spectrum at photon energy is of particular interest because Photon Enhanced Thermionic Emission (PETE) was recently suggested as an extremely efficient mechanism for solar energy conversion [15] [16] . It is based on emission of energetic electrons from a semiconductor cathode, which is illuminated and heated with solar radiation. For the PETE case Equation (5) shows that in the conventional Fowler regime for a temperature range from 300 to 500 K the QE value increases by only on 0.7%. In this temperature range, the QE value remains almost constant and does not exceed 35%. The proposed Anti-Fowler mechanism described below may improve the solar energy conversion only at low temperatures, therefore not practical for PETE based devices.

The Fermi level of thin metallic-like surface AL equilibrates with the bulk semiconductor Fermi level above around 100 K, therefore has a significant temperature dependence. As we show below, this leads to a sharp change of the temperature dependent photoemission threshold energy from surface AL, and affects significantly the QE photoemission dependence on temperature.

2.1. Room Temperature Threshold Energy of Photoemission for n-GaN

The threshold energy of photoemission is the difference between the energy of free electrons and the Fermi level. Therefore, the exact value of the Fermi and vacuum energy levels is a crucial parameter in the calculation of the threshold energy for photoemission. For a clean n-GaN (0001) surface the reported room temperature work function and electron affinity are 3.9 and 3.35 eV respectively [10] . In this case the Fermi energy is where is the energy of conduction band minimum. The value of E_F is in agreement with reported results [17] [18] obtained at room temperature, where the Fermi level was pinned by point defects near the n-GaN surface. At room temperature the work function of n-GaN covered by 0.5ML of Cs decreases to. Consequently, the position of the vacuum energy level in this case becomes

2.2. The Photoemission Threshold Energy at Arbitrary Temperatures

The position of Fermi level in semiconductors depends on the electronic structure, the concentration of donor and acceptor centers, and temperature [19] [20] . In n-type GaN the gallium vacancies are electron acceptors and thus play an active role in charge compensation, where the nitrogen vacancies act as shallow donors [21] . The dangling bonds of dislocations in n-GaN are acceptors which trap free electrons. A deep acceptor level located at the core of dislocations in n-GaN leads to an equivalent volume defect density of at a dislocation density of [22] . This density of acceptor states, practically coincides with the typical donor density measured for Si doped GaN; [10] [11] [12] hence the Si donors are practically fully compensated by the contribution of acceptors in GaN. The existence of the deeply pinned Fermi level is an additional evidence for the strong electron-hole compensation in n-GaN crystals.

This is in agreement with theories of electronic ALs in semiconductors that consider mainly the contributions of ionized shallow donors, while the contribution of deep acceptor centers is neglected [7] - [12] . This is a reasonable assumption because the deep acceptor states in GaN have weak interaction with the shallow donor states. The bandgap of GaN at room temperature is 3.4 eV. The measured energy levels of several deep acceptors found in GaN are

[23] : E(Li) = Ev + 0.75 eV for Li impurities which is around 0.95 eV lower than the Fermi energy E_F. The Be level around 1 eV lower than E_F, and Cs level is around 1.15 eV below E_F. These deep impurities have a characteristic size on the order of the lattice parameter; therefore their wave functions have a weak overlap with the wave functions of the shallow donor centers associated with ALs in GaN.

The analytical model for the temperature dependence of the Fermi energy in semiconductors is commonly derived assuming only one type of donors and one type of compensated acceptors [19] [20] . Following the discussion above, we adopt such an approximation for using the analytical model [19] for the Fermi level position in the partly compensated n-type semiconductor

(6)

here is the effective density of states in the conduction band, and are the donor and acceptor doped concentrations, is donor energy of thermal ionization, the degeneracy factor. In wurtzite GaN the effective density of states for electrons in the conduction band is For a typical concentration value of donor silicon atoms [10] [11] [12] , experimental ionization energy is [24] .

The Fermi level temperature dependence calculated according to Equation (6) is shown in Figure 1(a). In our calculations we assume that the bulk and surface accumulation are in equilibrium and the Fermi level is constant. However, at temperatures below 100K, it will take an infinite time for the accumulation to form. Therefore our calculations are valid only at temperatures above ~100K, as shown by the solid lines in Figure 1. This simplified picture is correct, if all the pinning defects have the same energy level and do not interact between themselves. However, in real crystals, defects are not identical. They interact with each other forming defect bands, which in n-GaN crystals have a width not less than 0.05 eV [25] . Therefore, we assume that with increasing temperature the Fermi energy level for the first time reaches the ceiling pinning band at the energy at temperature, and monotonically decreases with increasing temperature to around 300K. Further increase of temperature does not change the Fermi energy due to a strong pinning effect.

3. Results and Discussions

Based on the above calculations we present a simple and clear explanation for the increase of the quantum efficiency of low temperature photoemission, in comparison with the conventional Fowler regime. It is based on the Fermi level energy increase with decreasing temperature, and as a consequence the reduction of the photoemission threshold energy.

Based on the above calculation of the Fermi level, the temperature dependence of the photoemission threshold energy is calculated using the following expression:

(7)

The function is shown in Figure 1(b). According to Equation (7) the threshold energy decreases from at room temperature to at As seen from Figure 1(b) such a strong decrease of the photoemission threshold energy sharply in-

creases the QE with decreasing temperature (see Figure 1(c)). This behavior of photoemission at low temperatures we name the anti-Fowler regime. As known, from Fowler theory the QE photoemission in conventional photo-cathodes tends to suppress upon cooling, due to the sharp increase of internal resistance [26] . Our results show, that the anti-Fowler regime of photoemission can compensate this effect, and moreover can be used to create very efficient photo-cathodes at low temperatures. A sharp drop of the photoemission threshold energy at constant value of excitation energy explains the increase of QE photoemission (see Equation (5)) from 35 to about 55% in the transition from conventional Fowler regime at room temperature to anti-Fowler regime at low temperatures.

4. Conclusions

We have shown the physical mechanism for the increase of quantum efficiency photoemission from n-type semiconductors by formation of surface electron accumulation layers. The results report on increase of the QE from 0.35 to 0.55 when n-GaN is cooled from room temperature to around 100 K, which is in contrast to conventional Fowler regime. These results may allow highly efficient photo-cathodes operated at low temperatures.

Acknowledgements

This work was supported by the European Community FP7-Energy Project ProME³ThE²US² “Production Method of Electrical Energy by Enhanced Thermal Electron Emission by the Use of Superior Semiconductors”, Grant Agreement no. 308975, website: www.prometheus-energy.eu.

Cite this paper

Molotskii, M., Shimanovich, K. and Rosenwaks, Y. (2017) Anti-Fowler Temperature Regime in Photoemission from n-Type Semiconductors with Surface Accumulation Layer. Journal of Modern Physics, 8, 1020-1028. https://doi.org/10.4236/jmp.2017.87064

References