ABSTRACT

This paper follows the earlier paper Part I: Veringa, H. J. (September 2016), New Basic Theory of Gravity, Journal of Modern Physics 7 (1818-1828) in which a new model to describe the gravitational interaction between particles and its consequences on the attractive force between two masses is proposed. The basis for the analysis is a merger of Quantum theory and Relativity. Nowhere in the analysis, there is any need to deviate from well proven and successful concepts of both theories and rules of calculation, and no exotic new particles will have to be introduced. By doing so, it is demonstrated that, next to its local interactions of a multi-particle system, the Schrödinger equation leads to pairs of two and only two members. This solution is used as the invariant term in the quantized Dirac equation which gives gravitational interactions between members of the pairs. With this particular solution for the quantum-mechanical wave function, it is found that gravity is a second order effect operating over a long range. The emphasis of this paper is on the more precise justification of some of the basic assumptions made, on the historical context into which it should be placed, how it affects the ordering of our immediate environment and works on a cosmological scale. It is also found that the generator of gravity is contributing mass to particles that have gravitational interaction. This contribution is therefore related to cosmological parameters and will be further elucidated.

Keywords:

Gravity, Quantum Physics, Relativity, Cosmology

1. Introduction

This paper elaborates on the analyses made in an earlier publication published in September 2016 [1] . It was shown that the Schrödinger equation in free space and outside the influences of local interactions has a special solution for the wave equation of an ensemble of two particles. The two participants, or members, of this ensemble are shown to be connected into a pair which has to be seen as a pair potential, or a “generator” creating a sub-space, that manifests itself in the surroundings. Essential for this analysis is the assumed spherical symmetry. This pair potential is interpreted as the relativistically invariant mass density for a field described by the quantized Dirac equation. Quantization means that in the energy equation, as in this case the Dirac equation, the parameters like energy, momentum and the pair potential are replaced by their corresponding operators and are working on a wave function. This Dirac equation is then solved for an undefined number of pairs and it is found that a simple solution is possible which leads to an energy dedicated to the field for which the pair is responsible. It is most surprising that this solution, together with the appropriate boundary condition, gives precisely the right dependences for the gravity law as it has been discovered by Newtona few centuries ago.

The previous letter addresses the basic aspects, but some of the arguments can be expounded on and be put into a context of general insights into the micro-, as well as the macro cosmos. Then, later, some interesting clarifying analogies with daily life are offered. The analysis strongly connects with the famous debates between the founding fathers of Quantum theory and Relativity. Appreciation of these controversies shows that these historical, counter-intuitive, but at that time revolutionary, insights are all-important for the present development of the basic theory of gravity. When referring to formulas in the previous paper, Part I, the equations are indicated by (I. N).

2. Some Remarks on Pair Formation

2.1. Local and Non-Local Interaction

In Equation (I.1) of Part I, a pair forming quantum mechanical wave equation is postulated, but some further justification can be given.

The total wave function describing a particle under its local influences, 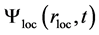, and its extension in free space, , is given by: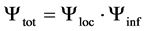. The coordinate is the position of the centre-of-mass of the particle inside the atom or nucleus or a solid object and the coordinate 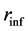is the position of the particle from the point of view of an outside observer. They therefore are mutually independent. In the same way we define the Hamilton operator as: 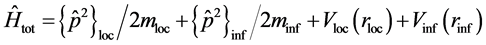. The masses and 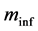are not necessarily the same. The 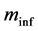is the mass to be identified for the particle as it can move freely around whereas 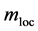is the mass of the particle under the influence of the local interactions, sometimes called “reduced mass”. It follows that:

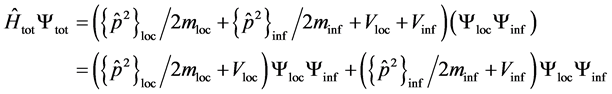(1)

Separating the local effect from the surroundings we can set:

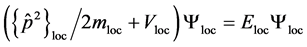(2a)

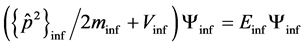. (2b)

The first Equation (2a) is the Schrödinger equation describing the behaviour of the particle in its local environment like in the nucleus or a solid where it has its individual interactions. The second Equation (2b) describes its movement or presence in the free space in which the particle or as part of a larger entity can move around. By taking 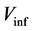as a constant it is assumed that the behaviour out of its local influences is taken into consideration. This second equation comes back as Equation (I.1) in part I. Further justification can be found in Section 4 of this letter.

The splitting up as in Equations (2a) and (2b) disconnects the local interaction of separate particles, as is normally done in quantum mechanics, from the movement or presence of the particle individually or as part of a larger entity. In what follows we will only consider the second equation as this gives the generator for the gravitational interaction. As we are interested in the effects of masses outside the local interactions we will from now on take for the mass 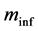the quantity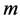, as it will also be the case for the coordinate.

2.2. Wave Functions

A general solution of a wave equation describing independent particles in spherical symmetry is initiated by the operator: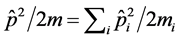, and reads:

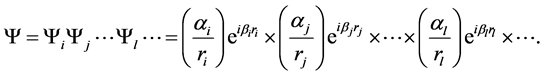(3)

But now we take the operator pair-wise with a pair identified by the set (ij) so that the operator becomes:

.

The factor 1/2 is to compensate for double counting and in the case of we set which represents the individual particle. With, as in Part I, we take and for the pair its own unique coordinate system with so that the solution becomes:

, (4)

The case of with and generates no gravitational interaction, but the operator does give gravitational interaction in the case of two, and only two, members in an ensemble with a solution (4) where the product is taken over all possible and unique pairs (ij). As the pairs are to be considered in their own unique coordinate system, there is no reason to consider all the pairs together but only the behaviour of a single pair and in the end to add up all the contributions of the pairs as long as co-variance, as in Equation (I.8), is preserved. As an illustration the wave function amplitude for a pair and independent particles as seen by one observer travelling along the line L is shown in Figure 1. From now on we will only

consider independent pair potentials of the pair ij, and we will replace the and by, and substitute the proposed solution into the base equation and get two separate conditions to be obeyed:, and .

It has been shown in part I that and so that for every value of the energy there will be a value for and the can adapt themselves. Therefore, whatever is the situation in which m_i and m_j find themselves, there is always a and a and they have no influence on the as long as. It means, finally, that the gravitational interaction is connected to an energy that is, apart from the separation between the members of the pair (R), independent of the situation these members are in. It is schematically shown in Figure 2, but it will need some further justification which will be given in paragraph 3.

There is freedom in the choice of the particles m_i, m_j, ・・・, m_l, ・・・. It can actuallly be anything like elementary particles, nuclei or even larger entities if, at least, we can describe such an entity by a single wave function in its own coordinate system and solve the equation to form a pair with another entity.

3. Microscopic Argument

Consider the atom with one outer electron of mass m that is circulating at some distance from the nucleus of mass M and experiencing a net charge Ze. The Schrödinger equation which incorporates both electrostatic interaction, given by and gravitational interaction, GMm/r reads as follows [2] :

(5)

from which it can be seen that the gravitational contribution is completely insignificant for any value of r. The general solution is:

, (6)

where is a polynomial, for instance for n = 1, , and . But now, as a “thought experiment” (Gedanken Experiment), we ignore the electrostatic contribution and take the general solution. It will be found that: and leading to: in the limit of n to infinity. According to the correspondence principle the electron, when moving in electro-statically determined orbits (s-, p-, d-states), has very high quantum numbers in the reference frame of gravity. Returning to the thought experiment we conclude that, if the atom is held together by gravitational forces only, the electron would have orbits at distances from the nucleus many orders of magnitude smaller than is actually the case. The argument above would however suggest that the electromagnetic force, although much larger than the gravitational interaction, manifests itself similarly in the entire space, but at some distance of the order of 1/a opposite charges start to compensate and electromagnetic forces will be suppressed and only gravitational forces start to dominate.

4. Solution of the Dirac Equation

In Part I, the quantized Dirac equation describes the interaction field in a pair ij which creates its own environment, or subspace, with coordinates and respectively. It ignores the movement of the individual particle.

This problem can simply be overcome by adding to the Dirac equation, while preserving co-variance, the energy operator, rest masses and the kinetic term which reads:

where l runs over all indices for individual particles, and r_l is the coordinate system of the observer.

These extra terms to the Dirac equation extends the solution to:

(7)

The number of pairs in the first product is numbered by ij if there are N particles numbered by l as in the second product. The term expresses a wave propagating in radial direction representing the moving of individual particles, but with reducing amplitude, or rather probability, as it progresses. If there is no interaction between members of the pairs we get the movement of the individual particles outside their local influence. This set-up has a very delicate interpretation. It shows that an observer from outside sees a pair creating a sub-space but cannot determine its structure inside. In the space inside, expressed by the coordinates r_ij and r_ji, gravitational interactions are occurring. Our observer only sees the separate interacting members of the pair with an energy due to this interaction as is shown schematically in Figure 3. It is as if we see two persons who have made a secret agreement (Schrödinger equation) and are, by acting as a pair, exchanging information (Dirac equation). We can see both persons but we cannot explain why they behave as they behave (Lorentz invariance). This latter invariance under Lorentz transformation has been shown to be the case in paragraph 7 of Part I.

5. Transfer of Energy

In the analysis in Part I going from Equations (I.12) to (I.14) terms are disappearing due to the solution proposed in Equation (1.11). But this has to be interpreted with caution. The pair probability density. in Equation (I.8) of part I represents a field carrying the gravitational energy. Therefore the disappearance of the generator at the right hand side of Equation (I.11), , involves exchange of energy from the pair to the surrounding space which is equal to the energy given in Equation (I.18). As a consequence, when the positive value for the energy is taken, the energy of the pair itself is reduced by the same amount. In that case the interaction between the members of the pair is attractive. The process is schematically shown in Figure 3. The transferred energy is the difference between the energy levels given in Figure 2.

The opposite situation in which the energy of the pair is positive, which in principle is allowed by the Dirac equation, is not possible when we assume that the energy of the vacuum, to be taken as the reference point, is zero. In this interpretation the interaction between mass and the surroundings is a means to transfer mass related energy (mc²) to gravitational energy. This transfer changes the rest masses of the pair but does not create new mass. The consequences at a larger scale are worked out in paragraph 10 of this letter.

If, however the vacuum state is, as it is generally believed, a non-zero energy state there might be energy available which increases with the interaction area, the white area in Figure 3, that can be transferred to the pair. The situation could be such that, when the distance between the members of the pair increases, the energy needed is reducing whereas the energy, or number of fluctuations carrying sufficient energy, is increasing. It means that at some separation distance of the members of the pair the interaction can become repulsive as the Dirac equation allows both negative and positive values for the interaction energy.

6. Transfer of Mass

In Part I a solution for the Schrödinger equation of a pair of particles for an observer at distances and from particle i and j. Now if we put our observer close by particle i, the second term in Equation (I.3) becomes negligible against the first term:

and:.

The Dirac equation in operator language now reads:

. (8)

Setting the right hand side to zero, a mass-less particle, we see an equation for a travelling wave at the speed of light. To get rid of the singularity we set for, and removing the first term on the left hand side gives the London Equation that explains the shielding of the inside of a type I superconducting material from the outside magnetic field: the “Meissner” effect. A similar thing can be imagined in this case with the -field for. The distance r_o can be identified as the distance from the centre to where local influences have no impact.

We can solve this equation, but it is not necessary as it can immediately be seen that it dedicates mass to the field in the vicinity of the particle which is equal to. As this is the mass to be attributed to the i-th particle due to another particle somewhere in the surroundings, we will have to add up over all particles which can make a pair with our particle, so with m₀ = m_i:

. (9)

The consequence is that either, a mass-free particle, or, with, as shown in Part I,:. First the equation allows that there are mass-free particles which make no pairs to generate gravity, like a photon. Second, the mass due to the effect under consideration becomes higher when increases and, most important, it is all the other mass in the surrounding that generates this mass in the field around the i-th particle. It is actually mass due to the field, but since the singularity moves with the particle the observer nearby can only interpret it as a mass contribution to the particle he is looking at. The conclusion taken here corresponds to Mach’s ideas about the effect of all physical entities in the universe.

It would be tempting to evaluate but, as we know already from observation, it is better to estimate the size or the extension of the particle only if this effect is responsible for the mass. The analysis concerns incredibly large and small numbers but leads to a surprising outcome.

Starting from and assuming that the mass of the universe is basically due to protons and neutrons with almost the same mass, so, and assuming there are N particles in the whole universe giving it a total mass of M we can set:

, (10)

Estimates of the universe on the basis of the analysis in section 10 give a total mass of the universe of 4 × 10⁵¹ kg, There are 6 × 10²⁶ protons in a kg; so we have 2 × 10⁷⁸ protons. is calculated in Part I at 2.3 × 10⁴ J×m/kg⁴ and the proton mass is 1.7 × 10⁻²⁷ kg. It leads to an estimate for the -value of 10⁻¹⁵ m, which is about the size of a proton (0.8 femtometers), [3] . An electron which is 1840 times lighter than the proton will, according to Equation (9), see the same surrounding as the proton, so its size would be smaller by the same factor.

Although the correspondence with measured data is surprisingly good, it is still a rough estimate and not without speculation. For instance, the sub-space due to the generator would be a quantum-mechanical reality, but it says nothing about its internal structure and interactions. The mass of the universe is rather uncertain in view of the discussion about dark matter, and the proton size, or how to define it, is not so obvious.

7. Macroscopic Analogy

Boys playing football next to a ditch are often unfortunate to find their ball in the water. Their usual course of action is to try throwing stones behind the ball from their point of view in the believe that the small water waves generated by the stones will, as they pass by the ball, push the ball a little bit towards them. A wise man passing by will tell them that it will not help as the only effect of the stones is moving the ball up and down.

However, it can be shown, after a lengthy calculation starting from the analysis of Mei [4] that when there are two balls at some distance apart in the water with a depth higher than the wavelength produced by the stones, and we throw stones between them and we keep on throwing these stones for a few thousand times, we will see the balls moving towards each other. The boys could therefore, by throwing stones in front of the ball, after a very long time get their ball back. In the analogy the ball dancing up and down is the mass that is attributed to the ball and the balls slowly meeting, little by little with the waves produced in between, is the attractive force due to gravity. Thus mass and gravity in this analogy are intimately connected which already followed from section 5 and 6.

8. Gravity as an Ordering Mechanism

It has been said before that the basic equation to form the pairs is valid at those locations where other influences like electromagnetic interactions are not important. In real life this means that gravitation interaction manifests itself where other forces are not the determining factor. Therefore in our real world we see that our direct vicinity has structures of forms that are changing over short distances like mountains, cities, sky scrapers, boats, forests etc. At larger distances, of the order of 100 kilometers the gravity becomes the dominant factor and bodies begin to take spherical shapes. Obviously the smaller the gravity is, as it is in smaller planets than earth, the structural variability will become larger. As has been said before, the electromagnetic interaction becoming insignificant in shaping the environment is not due to the form of the electrostatic interaction, which has basically the same shape as the gravitational interaction, but is due to the fact that positive and negative charges balance and compensate for their interaction starting already at short distances.

9. The Precession of the Mercury Perihelion Revisited

Consider a piece of matter m_o in a gravitational field generated by a larger mass M_o, and an observer far away out of this gravitational field, like on earth. This observer will interpret the real rest mass of m_o after he has taken it from a distance of R from the center of gravity to his free space. For the observer the rest mass is given by. Similarly the observer sees the other mass M₀, generating the gravity field, as. If the two masses M₀ and m₀ are encircling each other the observer will conclude that the force balance is given by:

. (11)

It is important to note here that, for the observer outside the gravity field of the two masses, the experience of equality of the gravitational mass and inertial mass is not valid anymore.

Also the observer sees that the time lapse T in the M₀-m₀ system is changed to and the length r is changed to .

When the observer on the planet Mercury, knowing that his mass is much smaller than the mass of the sun, sees that he has made one complete revolution around the sun, so:, the observer in outer space will see in accordance with Equation (11) that the planet Mercury has made a round trip of. Only the first order terms in with r = R at the end have been taken in the calculation. The outcome corresponds with the original analysis given by Einstein as the result of a more lengthy calculation.

10. Cosmological Consequences

The model presented here started from the Schrödinger equation where no boundary conditions are imposed on a system of particles. The subsequent finding of the pair formation as a result of this has consequences. First it means that the entire space, in which the particle pairs are embedded, is necessary for the interaction. Secondly, it is only the pairs that create the forces between them such that in Newton’s law the product of the masses gives rise to a total gravitational force. Also, the particular form of the solution of the Schrödinger equation, in which the wave function amplitude itself is used as an operator in the Dirac equation, leads to the R²-dependence. It is also important to remark that the gravitational interaction, leading to an interaction energy, is dependent on the product of the rest masses and independent of the speed in any direction in which one of the members of the pair or both are moving, even though the total mass of the pair changes relativistically.

We will calculate the energy balance of the universe assuming that, where matter is manifesting itself, the mass is distributed homogeneously. This assumption ignores any clustering of matter that will influence the energy, but it can be shown that this contribution is negligible against the energy that is dedicated to the relativistically defined masses (mc²).

To start with, relativistic masses are not taken into consideration. If the density of the rest mass is given by ρ₀ there are two contributions: potential energy, V, as the masses feel their gravitational pull to all other surrounding masses, and the kinetic energy, T, as the masses are moving relatively to each other [5] . Now:

(12a)

(12b)

where h is the so-called “Hubble constant”. It connects the expansion speed, v, of the matter with the distance, r, from the observer so that: v = hr.

We will take the sum as zero which means that, in the case of “flat, matter only” ultimately the universal expansion comes to rest, and we find:

(13)

This value of occurs as a proportionality constant in the Friedmann expansion equations which are based on the geodesic equations as derived from the Einstein field equation [5] . The last step is based on the assumption that the expansion speed is equal to the speed of light at the outer boundary of our cosmos.

It is interesting to evaluate this last equation, knowing that R/c is the radius of the universe in light seconds, that the average intergalactic density is about 1000 hydrogen atoms per cubic meter so that R/c = 0.3 × 10¹⁷ light seconds or about 10⁹ light years and that the generally accepted value of h is 2.3 × 10⁻¹⁸. These values are in the right order of the values assumed on the basis of telescopic observations.

Now we want to play the same game as above, but in a relativistic context. For this we should take the rest mass M₀ as the starting point in both calculations of the potential and the kinetic energy. First we will have to know what mass, M(R), is contained in a spherical volume with radius R:

(14)

In this equation the factor is connected to the mass increase due to the expansion speed. Just for the moment we can calculate the mass of the “observable” universe when and the apparent volume is: M/ρ₀. This is significantly larger than the non-relativistic number.

Making use of the fact that the interaction energy is dependent on the separation distance of the members of the pair and independent of the speed at which the members are moving, the potential energy is as above in Equation (15):

(15)

The kinetic energy cannot be evaluated by “Mv²/2” but more simply by:

(16)

Again, setting the sum equal to zero will give:

. (17)

This clearly differs from the non-relativistic value since the relativistic kinetic energy is so much larger than in the non relativistic scenario and it appears that the relativistic universe seen by our observer is “larger” by a factor of 2.1 or more heavy.

There is more than one way of interpreting this result. First we can say that from our observer’s point of view the energy due to expansion speeds in the outer areas is so high that it will never balance the gravitational energy, whereas for the observer in the outer areas, however, it could. From another point of view our observer sees that time is progressing more and more slowly in the outer areas and even, if the expansion speed will slow down, he will never be able to see it.

There have been speculations [6] [7] [8] that, by unknown mechanisms, the creation of mass is balanced by the loss in potential energy. In the present model this would mean that in Equation (16) we only use the Mc²-term:

(18)

In that case, surprisingly, the universe should be significantly larger, or heavier, than on the basis of the analysis of the “non relativistic” universe. But this latter argument should be considered with scepticism. Rest mass m₀ seen by an observer in free space changes from its value in a local gravity field by a factor of in which M is the mass with which m₀ is interacting and R the distance, but mass is not newly created. The argument suggests that there is a mechanism by which gravitational energy can be changed into new rest mass.

The factor mentioned is a small correction that plays no significant role in the analysis here, but it has been shown in paragraph 9 that it is of significance in calculating the precession of the perihelion of the planet Mercury around the sun.

11. The Bohr-Einstein Controversy

The model describing the gravitational interaction between particles has a some relation with the classical Bohr-Einstein dispute [9] . This dispute has been dealt with in many sessions between 1913 and 1930 as a subject of the Solvay conferences. The issue was Einstein’s belief that the quantum theory is an incomplete theory as he rejected the idea that positions in space-time could never be completely known. Einstein did not want to allow the uncertainty principle to necessitate an apparently random non-de- terministic mechanism by which the law of physics would be operating.

The controversy culminated in the well-known Einstein-Podolsky-Rosen Paradox, (EPR) of 1935 [10] which comes close to the ideas presented in this letter. Two particles have a common source, like two photons originating from one process in terms of space and time. From a quantum mechanical point of view the set of the two particles are represented by a joint wave function. One particle has orientation up (U) and the other down (D) and we do not know beforehand which of the two is up and which or down:

.

This is a superposition of two states of the ensemble. At some moment we do an experiment and find out that one of the particles is specified as “up”. From quantum theory we conclude that the other should be “down”. It might be that the system is influenced by the measurement so that the result “up” emerged, but the other particle is definitely not influenced and we know that it is characterized as “down”. It appears that the wave function has selected the option out of the superposition. From quantum mechanical point of view the process occurs independently of where in space and at which moment it takes place. For Einstein this was unacceptable and he suggested that the particle might have some “hidden variables” which we do not know and which decide the choice of the system. Niels Bohr could however justify his result by working out the situation in a more statistical way as quantum mechanics is basically a theory of probabilities which has been experimentally confirmed on several occasions. [11] .

We can now identify the solution for the pair potential in Equation (I.3) of Part I or, more generally, Equation (I.12), for a multi particle pair system, in a similar way as the “up/down” combination given above. As Max Born pointed out in a letter to Einstein: “There is a wholeness to a quantum events that persists over time and space and makes linkages possible”. These linkages, leading to the definition of the invariant in the Dirac equation, apparently, give rise to the gravitational interaction. So, nothing new proposed here, just a consequence of a classical debate between two scientists at the beginning of the previous century.

Apparently a single particle sees an environment and makes pairs with all of the particles around it. Suppose that at the other side of our galaxy two particles k, l annihilate. Suddenly the number of pairs reduces and this is seen by our particle. This change in the wave function:

generates a gravitational wave travelling through empty space at the speed of light and that adjusts to the new situation. But the information that the gravitational wave must start has already been exchanged between our particle with the observer and the annihilating pair. Again we end up in the same controversy as between Bohr and Einstein.

It is like a person somewhere far away sends me a message that something will be put into water so that I can go to the beach in The Netherlands and observe that there is some small rise of the sea level. If I will see anything, I have no idea where and when and in which way it originated, only that something has happened. Most likely the signal will be too small compared with the random disturbances. This analogy, however, is different from gravitational waves in that I have at least the sand of the beach as a reference level, whereas with gravitational waves such a thing does not exist.

12. Discussion

The present letter follows the previous one to illustrate some of the particular aspects of the theory of gravity developed, and which is based on well known and proven quantum mechanical- and relativity related aspects. Also some of the assumptions made would have needed justification and further working out. The first justification is the basic quantum mechanical wave equation describing the behaviour of particles without their direct short range interactions, which are usually taken care of in normal quantum mechanical considerations. An important first conclusion was that particles with a mass can be described as a single non interaction pair containing only two members. The individual members can make pairs with all other mass in its surrounding. This, already peculiar pair effect, is used in the Dirac equation which, in a quantum-mechanical representation, describes a field around these members. The second conclusion made is that energy is subtracted from the pair and gives rise to an attractive force between the two members of a pair. By setting this force equal to the well-known parameters of Newton’s third law, numerical values can be given to the main parameters found with the Dirac equation. It is then found that an observer watching the pair will see that the pair has two members, but he cannot see how they interact or exchange information, only that it leads to a force between them. This force is independent of the movement of the members.

The field that occurs due to the Dirac equation is not only present outside the particle but must also has its influence in areas where the particle mass manifests itself. Not much is known about what this field looks like and its local interactions, but the most simple approach would be to assume that the amplitude of the generator of this field is constant. The dependence on space coordinates of this field inside the outer boundary of the particle leads to the attribution of mass. This mass is then found to be a consequence of all the interactions which the single particle has with the surrounding mass in which the distance, apparently, plays no role. If we start from the values of the parameters derived from the gravitational interaction, and the known mass of a proton, its outer boundaries can be calculated which agree surprisingly well with the data found experimentally. However, it must be stressed that this last reasoning is speculative.

Going from small to large the theory that is developed has its consequences. One is that mass is to be attributed to a rest mass in a gravity field which in normal cases is merely negligible, but it has consequences on, for instance, the movement of the perihelion of Mercury during its encircling of the sun. It is also shown how mass and gravity are intimately connected and that the description of the cosmos at large distances is governed by the specific gravitational interaction between bodies constituting the universe.

One point, difficult to accept from logical point of view, is that members of a pair seem to have instantaneous contact no matter how far they are apart and therewith generate the interaction field that gives rise to gravity. Gravity waves move at the speed of light or slightly less, depending on the mass density it is moving through, but its generator works apparently without delay. The situation is the same as the classical debate in the previous century between Einstein and Bohr and have remained to be an issue which is hard to believe but more than once shown to be true.

Another point to remark here is the occurrence of a generator creating a subspace. It follows unambiguously from the Schrödinger equation but nothing can be said about its internal structure where particles are entangled and apparently exchange information. This might be close by the idea of Einstein about “hidden variables”.

Further causality is of importance to keep in mind. The model starts from the fact that there are masses, and it is seen that they can form pairs and generate gravity. It yields numerical data about the masses following gravitational parameters. The strength of the model is the consistency of the data with what we observe in reality.

13. Conclusion

A new theory about gravity is developed which explains the particular aspects Newton’s third law. It is found that nowhere in the development of the theory there was any need to deviate from well established existing concepts in quantum-mechanics and relativity and rules of calculation. Some of the debates that originated from these insights could be given a place in the concepts developed and helped in the interpretation of the results. According to the theory developed gravity is a relativistic quantum effect that manifests itself at both small scale, the scale of our daily life and also on a cosmological scale. Taking the gravity constant as starting point, both microscopic and cosmological parameters can be derived that correspond well with the observations.

Cite this paper

Veringa, H.J. (2016) Part II of New Basic Theory of Gravity. Journal of Modern Physics, 7, 2266-2280. http://dx.doi.org/10.4236/jmp.2016.716195

References

NOTES

^*The equation citations of Equations (I.1, I.3, I.8, I.11-I.14, I.18) are from the article in the following link: http://dx.doi.org/10.4236/jmp.2016.713162.