ABSTRACT

Basing on the energy conservation, an analysis method on the gravity of antimatter is proposed by investigating the change of potential energy during high energy photon transfers to electron and positron in earth gravity field. Potential energy equations are deducted and proved that the force between matter and antimatter is attractive, and then the force between antimatter and antimatter is proved to be attractive too. So the gravity is attractive without considering matter or antimatter.

Keywords:

Antimatter, Gravitational Potential, Gravity, Energy Conservation, Attraction

1. Introduction

The gravitational behavior of antimatter is still unknown since antimatter was first discovered in 1932. The equivalence principle is a cornerstone of General Relativity and all metric theories of gravity [1] . According to General Relativity, the inertial and gravitational masses are equality, both to matter and to antimatter. The Einsteinian view of gravity is a geometric phenomenon which means the curvature of curved space-time. By the equivalence principle, antimatter will attract both matter and antimatter at the same rate that matter attracts matter and antimatter.

In 1958, Morrison [2] considered the energy conservation of a matter-anti- matter pair created at the Earth’s surface. The pair is raised adiabatically to a height with no change of energy. Then the pair’s annihilation would produce a blue-shifted photonic energy in going back to the Earth’s surface if the gravity of antimatter is negative, thus energy conservation is violated, so the gravity of antimatter is positive. Schiff [3] [4] deduced that positrons and electrons have the same positive inertial mass and gravitational mass from Eӧtvӧs’s experiment and Newton’s third law. Dehnen and Ebner [5] indicated that the properties of an antiparticle system should be the same as those of a particle system by the theories of CPT symmetry which suggests that a pair of antiparticles should interact gravitationally in the same manner as a pair of particles. Among other consequences, CPT conservation implies that the inertial masses of a particle and its corresponding antiparticle are equal. But Tasson [6] summarized several possibilities and the implications of Lorentz and CPT violation for antimatter gravity in the context of the gravitational Standard-Model Extension (SME).

Mark Kowitt [7] based on an analogy with electron and hole dynamics in semiconductors, generalized Dirac’s relativistic electron equation to include a gravitational interaction using an electromagnetic-type approximation of the gravitational potential, extended Dirac’s deduction of antimatter parameters to include the possibility of gravitational repulsion between matter and antimatter with gravitational and inertial masses decoupled.

Santilli in 1994 [8] , Cabbolet in 2010 [9] , Villata in 2011 [10] , predicted antigravity based on classical isodual theory, elementary process theory and Villata’s theory respectively. Villata found that gravitational interaction between matter and antimatter is a mutual repulsion when CPT symmetry and General Relativity theory is applied. There are many arguments on antimatter gravity now.

In a large number of laboratory and astronomical tests, the gravitational interaction of antimatter with matter or antimatter has not been conclusively observed by physicists. It is difficult to directly observe gravitational forces at the particle level. There are many huge challenges on measuring the gravity of antimatter at present technology. The only direct experimental result [11] on antimatter gravity comes from Supernova 1987A which is in the Large Magellanic Cloud emitted both neutrinos and antineutrinos. Some neutrinos and antineutrinos took about 160,000 years to reach the Earth, and while traveling were bent from a “straight line” path by the gravity from our own galaxy. The bending with gravity changed the time needed to reach Earth by about 5 months, yet both the neutrinos and the antineutrinos reached Earth at roughly within the same 12 second interval. This shows that the neutrinos and antineutrinos “fell” similarly, to a very high level of precision [12] .

Although unlike ordinary matter, the behavior of antimatter particles in a gravitational field has never been directly measured experimentally, CERN try to test it with antihydrogen. Phillips [13] describes a possible measurement of this force by measuring the phase shift of neutral antimatter in a transmission-grat- ing interferometer caused by the Earth’s gravitational field.

Photons are observed to be attracted to matter, exactly in accordance with the theory of General Relativity [14] . But it is remained unanswered that the direction of gravitational force between antimatter and ordinary matter, antimatter and antimatter.

This paper discusses the gravitational property of antimatter and compares it with that of matter, eventually presents a different method to prove the sign of antimatter gravity is positive.

2. Antimatter Produce

Danielson [15] introduced the progress on producing low-energy antimatter such as positrons and antiprotons, and the development of new plasma-based techniques to accumulate, manipulate, and deliver antiparticles for specific applications.

So we can assume that high-energy 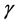ray photon becomes electron and positron through some mechanism. The formula that describes 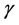ray photon transfers to electron and positron under special conditions is as follow:

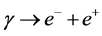(1)

where 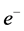is electron, 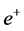is positron.

Generally, positron 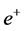can be produced from a Surko-type [16] source and accumulator. In early of 2016, Xu et al. [17] presented a method of experimental generation of ultrashort MeV electron and positron beams with high intensity and high density using a setup in which a compact laser beam above an argon gas jet emitted from a supersonic conical nozzle to produce electrons which are directed onto a high-Z solid target behind the gas jet to generate electron-posi- tron pairs. This means high energy 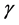ray photon can transfer into some kind of matter and antimatter, so the follow formula can be gained.

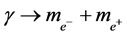(2)

3. Analysis on Gravity between Matter and Antimatter

According to Newton’s gravity theory, the attractive force between the Earth and matter is

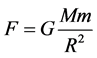(3)

where 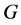is the universal gravitational constant, 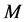is the mass of the Earth, 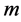is the mass of the matter, and 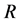is the distance of the matter from the center of the Earth.

The potential of gravity field of the Earth is

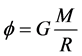(4)

The potential energy of the Earth gravity field is

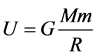(5)

Assume no energy dissipate to environment, due to energy conservation, the energy of photon before and after transformation into matter and antimatter is

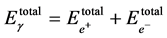(6)

So the mass of generated matter and antimatter satisfies the following equation

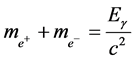(7)

Assume that the mass of matter and antimatter is approximately same, so we can get the following equation

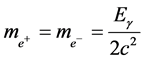(8)

Then the mass energy for moving matter and antimatter is

(9)

where c is the speed of light in vacuum. The rest mass energy of ray photon is

(10)

And according to Einstein’s mass energy equation, the potential energy of ray photon under the Earth gravity field is as follow,

(11)

where is Planck’s constant. The total energy of electron is as follow,

(12)

The total energy of positron is as follow,

(13)

So for energy conservation before and after ray photon transfer into electron and positron , follow equation is gained

(14)

Consider Equation (7), (11) and (14), the potential energy of ray photon before and after transfers into electron and positron is gained as follow,

(15)

So it can be simplified to

(16)

If the antimatter gravity is repulsive from matter, the Equation (15) becomes

(17)

So it can be simplified to

(18)

Above equation is paradox, it conflicts with that photon has potential energy in gravitational field, if the antimatter have no interaction with gravity field, Equation (15) becomes

(19)

The Equation (19) is paradox too, it also conflicts with that photon has potential energy in gravitational field and should be singularity at one place. So it can be concluded that the antimatter gravity must be positive, this means that the gravitational force between matter and antimatter is attractive and is same as that between matter and matter.

It is proved that the gravity between matter and antimatter is attractive, so with comparing the gravitational field produced by matter with the corresponding gravitational field produced by antimatter, some deductions can be made as follows:

1) The gravity field generated by antimatter is same as that generated by matter.

2) The gravity force is the interaction of matter with gravity field, according to Einstein’s theory that the space-time is changed in gravity field.

3) The interaction of antimatter with gravity field is same with matter.

Hence, the gravity force between antimatter and antimatter is attractive, as shown in Figure 1.

Assume there are matter and antimatter bodies with same mass. The Figure 1(a) shows the gravity potential field produced by matter body. The gravity potential on the surface of the matter body is maximum, it gradually reduces to zero from the surface to infinite distance. The gravity potential field is central symmetry. The Figure 1(b) shows the potential gravity field produced by antimatter body. It is similar with Figure 1(a). When two matter bodies at a certain distance, the gravity potential field produced by them is shown in Figure 1(c). The gravity potential is zero at the middle of two matter bodies and infinite distance. For one matter body in Figure 1(c), the gravity potential in the inner side is less than the outer side in same distance apart from each body. That the gravity force between two bodies is pointing to each other, it means the sign of the gravity force is positive. The direction of gravity force is consistent with the maximum gradient of gravity potential field. Even though the gravity potential field is central symmetry on the middle distance of two matter bodies, it is not central symmetry for each matter body. As shown in Figure 1(d), according to the deduction previously, when one matter body is replaced by a same mass antimatter body at one side, the gravity potential field will not change and the gravity force will not change also. It means the interaction of gravity field to matter and antimatter is same, so the gravity field can not distinguish matter and antimatter. So in other word, the gravity potential field can not make difference between matter and antimatter. If the matter body in Figure 1(d) is replaced by a same mass antimatter body. The gravity potential field will not change and the gravity force will not change also as shown in Figure 1(e). Eventually, it can be concluded that the sign of antimatter gravity is positive.

A strongly proof is that photons are their own antiparticles, and in all respects behave exactly symmetrically with respect to matter and antimatter particles. Another proof is that antiproton interaction is attractive, which means matter

and antimatter is symmetry [18] .

4. Conclusion

Based on energy conservation theory, an analysis is made on the gravity of antimatter. It is proved that the gravity between matter and antimatter is attractive to each other, which is same with the gravity between matter and matter. By using Einstein’s space-time theory, it is deducted that the gravity between antimatter and antimatter is same with the gravity between matter and matter also. In other words, the sign of antimatter gravity would be exactly the same as normal matter.

Cite this paper

Wang, Y.N. and Wang, Y.J. (2017) An Analysis on the Sign of Gravity of Antimatter. Journal of Modern Physics, 8, 156-162. https://doi.org/10.4236/jmp.2017.82014

References