ABSTRACT

This article proposes the potential energy function of nucleon in nucleus, derives the expression equation of nuclear force, shows that nucleus has the shell structure by the solving the Schrödinger equation of nucleon, obtains the magic numbers, and interprets the past experimental results in theory; for example the radius of nucleus is proportional to the cubic root of nucleon number, the nuclear force is repulsive in the depths of nucleus and attractive in the surface layer, and the variation of average binding energy of nucleons with the nucleon number.

Keywords:

Potential Energy of Nucleon, Nuclear Force, Shell Structure, Average Binding Energy

1. Introduction

The study on nuclear force and nuclear structure is the center subject of nuclear physics. Although the liquid drop model, the shell model and other models of nucleus had been put forward on the basis of experiments long ago [1] [2] , the models have been not united in theory due to the absence of the potential energy function of nucleon in nucleus by now. In the following we will propose the potential energy function of nucleon in nucleus, derive the expression equation of nuclear force, show that nucleus has the shell structure by the solving the Schrödinger equation of nucleon, obtain the magic numbers, and interpret the past experimental results in theory; for example the radius of nucleus is proportional to the cubic root of nucleon number, the nuclear force is repulsive in the depths of nucleus and attractive in the surface layer, the variation of average binding energy of nucleons with the nucleon number.

2. The Potential Energy Function of Nucleon

Since the nuclear force is independent of charge, the nucleons (protons and neutrons) could be considered as identical point particles, and the mass of free nucleon is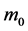. Suppose the number of nucleons in the nucleus is N, the radius of the nucleus is R, and the distance from the nuclear center to the nucleon is r, 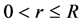, construct the potential energy function of the nucleon as follows

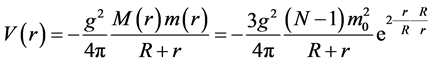(1)

where 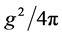is the strong interaction constant, the interaction mass of nucleon

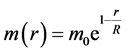(2)

and the interaction mass of the nucleus within the radius r

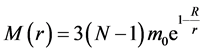(3)

the introduction of factor 3 is due to the strong interaction with the three colors [3] .

Substituting N for 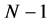in the equation above gives the mass density of nucleus:

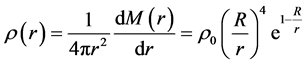(4)

where

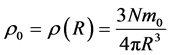(5)

is both the average mass density of nucleus and the mass density on its border. So

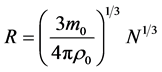(6)

this shows the radius of nucleus is proportional to the cubic root of nucleon number, this is consistent with the experiments [4] , and there is

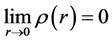(7)

3. The Nuclear Force and Nuclear Structure

The expression equation of nuclear force can be obtained from Equation (1):

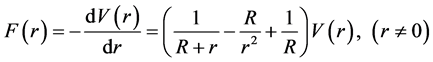(8)

Obviously, the nuclear force is short-range, and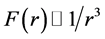. Take 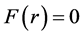gives

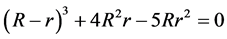(9)

So there is

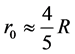(10)

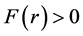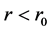There is when, the nuclear force is repulsive, and when, the nuclear force is attractive. According to the above analysis and notice

(11)

we can draw the function curve of the potential energy of nucleon and the nuclear structure diagram, as shown in Figure 1 and Figure 2. Therefore the nucleus could be considered as an incompressible “liquid drop”.

4. The Shell Structure of Nucleus

In the following we show that the nucleus has the shell structure and explain why the nuclear force changes from the repulsion to the attraction with the increase of the ra-

dius. Take, the potential energy of nucleon can be rewritten as

(12)

where, and the eigenvalue equation of the Hamilton operator of nucleon is

(13)

Write

(14)

the Equation (13) can be divided into the two equations as follows:

(15)

(16)

where. The Equation (15) is the eigenvalue equation of the angular momentum square as operator, and the solution is the spherical harmonic function:

(17)

where is the associated Legendre polynomial, is the normalized constant. The Equation (16) is called the radial equation. Write, the Equation (16) becomes

(18)

There is for the nucleon in bound state, write

, , , (19)

the Equation (18) becomes

(20)

Substituting the form solution into the equation above gives

(21)

Write, notice, the equation above can be rewritten as

(22)

According to the theory of ordinary differential equations the above equation has the series solution as follows:

(23)

where

is the associated Le Gail polynomial, , is the principal quantum number, and the energy eigenvalue is

(24)

Notice

, (25)

the radial wave function of nucleon is

(26)

where, and the normalized constant

(27)

where. So the wave function of nucleon is

(28)

Since the nuclear force is mainly in the radial direction we introduce the radial quantum number. The greater the radial quantum number, the farther the distance of nucleon from the nuclear center. Consider the coupling of spin and orbital angular momentum, Hamilton operator in Equation (13) should be rewritten as [5]

(29)

So the angular momentum quantum number is, and the degeneracy of

each subshell is. The implies the force on the nucleon is a bound force, and implies the force on the nucleon is a repulsive force, thereby, the energy

level corresponding to is below the energy level corresponding to. Thus we can write the quantum states and the allowable nucleon number in each shell [4] :

The first shell:; 2

The second shell:,; 6

The third shell:, ,; 12

The fourth shell:; 8

The fifth shell:, , ,; 22

The sixth shell:, , , ,; 32

The seventh shell:, , , , ,; 44

…,

So the total number of nucleons fulfilled the first shell equals 2, the total number of nucleons fulfilled the first two shells equals 8, the total number of nucleons fulfilled the first three shells equals 20, and so on, and these numbers are the called magic numbers: [4] . Thus we have shown the nucleus has the shell structure. And now we explain why the nuclear force changes from the repulsion to the attraction with the increase of the radius.

We know that nucleons are fermions, there is the repulsion between them according to the Pauli Exclusion Principle, at the same time there is the attraction due to the exchange of meson between them. The above calculation shows that the higher the shell level, the more the nucleons, except the fourth shell. In other words, the nucleon number increases with the increase of the radius, the attraction due to the exchange of meson between nucleons becomes stronger. In this way, the attraction is weaker than the repulsion when, the nuclear force is repulsive, but the attraction is stronger than the repulsion when, the nuclear force is the bound.

Since the distribution probability of nucleons is independent of the magnetic

quantum number m, the shape of fulfilled nucleus is spherical, and the shape of unfulfilled nucleus is ellipsoid [6] - [10] .

5. The Average Binding Energy of Nucleon

For simplicity, suppose every energy level is fulfilled by nucleons, the Equation (24) gives the average binding energy of nucleon as follows:

(30)

where k is the number of energy levels fulfilled by nucleons. From the equation above we see that the average binding energy of nucleons of the medium nucleus with major nucleons is greater than that of the light nucleus with fewer nucleons, this is consistent with the experiments. But, in the heavy nucleus whose nucleon number more than 100, some nucleons are located in the repulsive region of with the increase of nucleon number, and their energy levels are elevated, so, the average binding energy of the heavy nucleus becomes smaller. This is also consistent with the experiments [4] - [10] , as shown in Figure 3, which is an experimental curve.

6. Conclusion

The above analysis shows that a series of results consistent with the experiments can be

derived from the potential energy function of nucleon as shown in the Equation (1), therefore, the potential energy function of nucleon given by this article is reasonable.

Cite this paper

Liang, B. (2016) The Potential Energy of Nucleon and Nuclear Structure. Journal of Modern Physics, 7, 1866-1873. http://dx.doi.org/10.4236/jmp.2016.714165

References