ABSTRACT

The quantum metric tensor was introduced for defining the distance in the parameter space of a system. However, it is also useful for other purposes, like predicting quantum phase transitions. Due to the physical information this tensor provides, its gauge independence sounds reasonable. Moreover, its original construction was made by looking for this gauge independence. The aim of this paper, however, is to prove that the quantum metric tensor does depend on the gauge. In addition, a real gauge invariant quantum metric tensor is introduced. A related concept is the quantum fidelity, which is also shown to depend on the gauge in this paper. The gauge dependences are explicitly shown by computing the quantum metric tensor and the quantum fidelity of the Landau problem in different gauges. Then, a real gauge independent metric tensor is proposed and computed for the same Landau problem. Since the gauge dependences have not been observed before, the results of this paper might lead to a new study of topics that are believed to be completely understood.

Keywords:

Landau problem, Quantum Metric Tensor, Gauge Dependence, Quantum Fidelity

1. Introduction

The main purpose for constructing the quantum metric tensor (QMT) was to define a distance in the system’s parameter space [1] and recently it has been shown that this metric tensor can be obtained using the renormalization flow equations [2] . That is why it is not surprising that the QMT is related to the quantum fidelity (QF), which is also used for measuring the distance between states [3] , even though some studies have shown that the QMT can also be used to predict quantum phase transitions [4] [5] . In [6] , the critical exponents for systems that present continuous second order phase transitions are defined. Moreover, the geodesics induced by the QMT have been useful for analyzing the phase transitions [7] . In general, the Riemannian structure introduced by the QMT has been studied in some particular systems, seen for example [7] . The authors of [8] make an analysis of the Gaussian curvature induced by the QMT and describe the critical phenomena in relation with this curvature.

In general, there has been much interest in the geometrical properties of quantum systems. In [9] it is shown that the mass can be seen as a geometric effect in the Hilbert space. Reference [10] proposes a formalism of quantum space geometry for generalized coherent states and analyzes it with known results of the symmetry AdS/CFT. On the other hand, in Ref. [11] a numerical analysis of the fractional quantum Hall effect related with geometric stability is performed. Continuing with the numerical computation, in [12] , it is presented a method to compute the fidelity susceptibility (a particular case of the QMT) with the Monte Carlo method.

The QMT was constructed by looking for a gauge independence [1] and, in fact, it was partially done. However, when we consider some kinds of gauge transformations, the QMT is not invariant. Nevertheless, in current works the gauge dependence is overtly assumed. Since this gauge dependence has not been observed before, we explain its origin and propose a real gauge invariant quantum metric tensor. On the other hand, the QF is a similar concept that is also useful to measure a distance in the parameter’s space of a system, and as well as the QMT, it sounds reasonable that it does not depend on the gauge. However, it is proved that it is not always the case.

In this paper, we use the Landau problem to show the gauge dependence of the QMT and the QF. For this reason, in Section 2 we describe the Landau problem in the symmetric gauge. Section 3 shows the QMT for one of the ground states in different gauges. While Section 4 introduces a gauge independent definition of the QMT, Section 5 shows the calculation of this new definition for the Landau problem. On the other hand, Section 6 shows the gauge dependence of the QF and explains its origin. Finally, a discussion and our conclusions are written in Section 6.

2. The Landau Problem

The Landau problem [13] consists on a charged particle interacting with a constant and homogeneous magnetic field,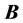. If we consider a particle of unitary mass and charge 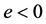the Hamiltonian of the system is given by

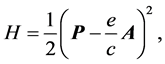(1)

where 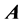is the vector potential, such that. If we assume that the magnetic field points in the z direction i.e. 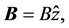then the movement in z will be constant, and we can ignore it. For the quantum case, the energy spectrum of the Landau problem is given by [13]

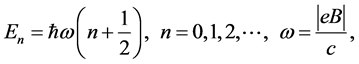(2)

these 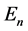are the well-known Landau levels. However, for the Landau problem each level is infinitely degenerated. Therefore, we need an additional Hermitian operator, which commutes with H, to label the states. If we choose the symmetric gauge, i.e.

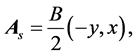(3)

we can select the angular momentum in the z direction, 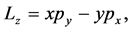as the second operator. In this gauge, the ground states are given by [14]

(4)

where m is a label for the angular momentum in the z direction, such that

(5)

In this case, we see that the wavefunction depends on the parameters space and the physical space x.

3. The Quantum Metric Tensor of the Landau Problem

The QMT, 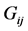, is useful to define a distance in the system’s parameter space [1] . If our quantum system depends on n parameters, 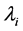, the QMT is given by

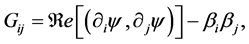(6)

where is the state of the system, and

(7)

with this definition, the corresponding distance will be [1]

(8)

It is proved that the QMT is gauge invariant [1] , nevertheless, this proof is not the most general. The demonstration assumes some specific features of the phase difference caused by a gauge transformation. In order to show the gauge dependence of the QMT, we need to compute it in different gauges. The first calculations will be in the symmetric gauge.

3.1. The Quantum Metric Tensor in the Symmetric Gauge

For the purpose of this paper, it is sufficient to consider only the variation of B, therefore the parameter space will be 1-dimensional, with, and setting is appropriate. We will compute the QMT of the ground state with, then, by using the state presented in Equation (4), the first term of the definition will be

(9)

whereas

(10)

therefore

(11)

3.2. Comparison of the Quantum Metric Tensor in Different Gauges

In order to prove the gauge dependence of the QMT, we make the calculation in different gauges. It is known [15] that when two gauges are related by

(12)

the corresponding wave functions obey

(13)

According to the theory [1] [16] , since the wave functions are related just by a change of phase, the QMTs should coincide. To explicitly show that this match does not always occur, we choose as the symmetric gauge and

(14)

This particular allows us to examine several gauges using g as a parameter. In particular, when we set, we obtain the Landau Gauge given by

(15)

and with we recover the symmetric gauge. In this case, depends on the parameter B and the physical space.

Now, in Equation (13), we set as the ground state in the symmetric gauge, then the ground state with in the new gauge will be

(16)

From Equation (16) and the definition of the QMT, we compute that

(17)

The presence of g in Equation (17) clearly implies gauge dependence. This gauge dependence is inherited by the distance in the parameter space. This means that we do not have a gauge independent distance in the parameter space. In the specific case of Equation (17) the distance is minimum when we work in the symmetric gauge (), and it increases indefinitely as we increase the absolute value of g. It is worth to notice, however, that the QMT diverges when for any value of g.

4. Real Gauge Invariant Quantum Metric Tensor

If we perform a gauge transformation in the parameter space, given by

(18)

then changes as

(19)

It has been assumed that the phase, as well as its derivatives, can be taken outside of the internal product. Therefore, we would be able to simplify Equation (19) to

(20)

when Equation (20) is valid, the tensor presented in Equation (6) is gauge invariant. This means that the QMT is gauge invariant when is independent of the measure of the internal product.

However, some phases, and its derivatives, may depend on the physical space, , or any other operators. See, for example, the phase in Equation (16). In these cases, Equation (19) cannot be simplified; thus, the tensor of Equation (6) is no longer gauge invariant. It is worth to notice that Equation (12) and Equation (20) seem to give the same transformation rule. However, in Equation (12) the derivatives are computed respect to the coordinates, while in Equation (20), one derives respect to the parameters.

Before constructing the real gauge invariant QMT, we note that Equation (6) can be written as

(21)

or, in the representation of coordinates

(22)

because is real. Then, by looking Equation (20), we realize that transforms like a connection when is independent of the internal product. This means that the QMT of Equation (21) is constructed with covariant derivatives, using as the connection. Nonetheless, in the general case transforms like it is shown in Equation (19), and it cannot be used as the connection.

For constructing the gauge invariant QMT, we need a function that transforms like

(23)

when we perform a change of gauge given by Equation (18). With this new connection, the gauge invariant QMT will be

(24)

or

(25)

In Equations (24) and (25), we recognize the covariant derivative, , given by

(26)

which transforms like

(27)

under a change of gauge. Using the covariant derivative, the QMT takes the form

(28)

Equation (28) defines a gauge invariant QMT. Since Equation (27) is valid, then Equation (28) will always be gauge independent. Here we can see that if, instead of Equation (27), we perform a no Abelian gauge transformation we would generalize the QMT to a no abelian QMT.

However, we need to find the correct connection that transforms like it is shown in Equation (23). The form of the new connection will depend on the specific problem to be analyzed. must reduce to in the case that can be taken outside of the internal product. Therefore, the new QMT must also reduce to the one presented in Equation (6) when is independent of the measure of the internal product. In the following section we present the for the example studied in this paper.

5. Gauge Invariant Quantum Metric Tensor of the Landau Problem

Continuing with the example presented in Section 3.2, the new QMT is given by

(29)

The fact that in the usual case, suggests that we must set

(30)

therefore, according to Equation (23), and using that, we find

(31)

thus, under the transformation of Equation (18), we get

(32)

Applying Equation (32) to the state given by Equation (16), we obtain

(33)

for any gauge. That is, the QMT proposed in this paper is gauge independent.

6. Gauge Dependence of the Quantum Fidelity

As it was mentioned in the introduction, the QF is also useful to measure the distance between states. If the quantum system depends on n parameters, the QF is given by [2]

(34)

where is the state of the system. Continuing with the Landau problem, if we compute the QF using the state given by (16), we obtain that

. (35)

In Equation (35) we can see dependence with the parameter g, therefore the QF also depends on the gauge chosen. This dependence occurs for the same reason that it appears in the QMT i.e. the phase difference is not independent of the internal product. If we start with a gauge whose state vector is the QF will be

(36)

if we now perform the gauge transformation given by Equation (18), the QF fidelity will take the form

(37)

again, when the phase can be taken outside of the internal product Equation (37) simplifies to

(38)

and the fidelities in different gauges coincide. However, for more general gauges, like the presented in the example studied here, we cannot take the phase outside and, therefore, the fidelities do not coincide.

7. Discussion and Conclusions

We explicitly showed that the QMT and the QF depend on the gauge. This dependence is directly related to the phase difference between the wave functions in different gauges: when the change of gauge introduces a phase whose derivatives can be taken outside of the internal product, both, the QMT and the QF are invariant. However, when general phases are considered, they depend on the gauge.

We also proposed a real gauge invariant QMT by defining a new connection that transforms according to Equation (23). Despite the gauge independence, the connection was not explicitly given, and the form of will depend on the specific problem to be studied. In the example shown in this paper, i.e. the Landau Problem, we successfully proposed the correct for obtaining a gauge invariant QMT.As it was pointed out before, the QMT and the QF have several applications in physics. The fact that the QMT and the QF depend on the gauge can give rise to new studies in the topics that apply this two tools. An important case is the applicability of the QMT for predicting quantum phase transitions. In the example studied in this paper, the gauge independent QMT, as well as the gauge dependent QMT, diverges for the same value of the field B in any gauge. This fact suggests that both QMTs are useful for predicting quantum phase transitions. However, the chosen gauge in this example is not the most general, and further studies are necessary.

Acknowledgements

This work was partially supported by DGAPA-PAPIIT grant IN103716; CONACyT project 237503, and scholarship 419420. We also wish to acknowledge Unidad de Posgrado, UNAM for the support and the workshop “Academic Writing” during the preparation of this paper.

Cite this paper

Alvarez-Jiménez, J. and Vergara, J.D. (2016) Gauge Invariance, the Quantum Metric Tensor and the Quantum Fidelity. Journal of Modern Physics, 7, 1627-1634. http://dx.doi.org/10.4236/jmp.2016.713147

References