Journal of Modern Physics
Vol.07 No.11(2016), Article ID:68150,4 pages
10.4236/jmp.2016.711115
Higgs-Like Boson and Bound State of Gauge Bosons W+W- II
F. C. Hoh
Retired, Dragarbrunnsg. 55C, 75320 Uppsala, Sweden

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 May 2016; accepted 8 July 2016; published 11 July 2016
ABSTRACT
The Higgs-like boson discovered at CERN in 2012 is tentatively assigned to a newly found bound state of two charged gauge bosons W+W- with a mass of EB ≈ 117 GeV, much closer to the measured 125 GeV than 110 GeV predicted in a paper with the same title earlier this year. The improvement is due to a shift from the earlier SU(2) representation assignment for the gauge bosons to the more realistic SU(3) one and that the computations are carried out with much greater accuracy.
Keywords:
Bound State of W+W-, Higgs-Like Boson, SU(3) Group

1. Introduction
This note is a further development of the recent paper [1] , in which the Higgs-like boson H(125) discovered in 2012 with mass 125.09 GeV [2] was tentatively assigned to a bound state of two charged gauge bosons W+W- with a mass of EB ≈ 110 GeV. The starting point is the action for gauge bosons ( [3] , 7.1.2),
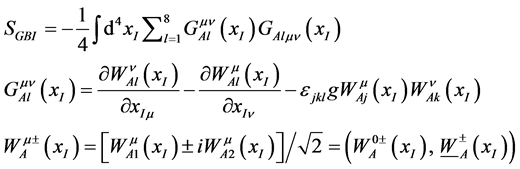 (1)
(1)
where 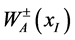 denotes the charged gauge bosons and the superscript 0 its time component. In ( [1] , 1), however, the flavour index l was limited to run from 1 to 3 to reflect the assumption that these gauge bosons W+W- belong to a SU(2) representation, the lowest ranked one of a SU group. In this representation, the other gauge bosons, the massive neutral Z and the massless A are absent.
denotes the charged gauge bosons and the superscript 0 its time component. In ( [1] , 1), however, the flavour index l was limited to run from 1 to 3 to reflect the assumption that these gauge bosons W+W- belong to a SU(2) representation, the lowest ranked one of a SU group. In this representation, the other gauge bosons, the massive neutral Z and the massless A are absent.
2. SU(2) vs SU(3)
Now, H(125) was generated in high energy proton-proton collisions in which all these 4 gauge bosons appear and a SU(3) representation is more appropriate. The 4 extra gauge bosons of the 8 gauge bosons in this representation degenerate to the 4 observed ones ( [3] , §7.2.3).
Further development is the same as that in [1] with the change of SU(2) to SU(3). This change only affects the running coupling constant ( [1] , 19) where the coefficient of the logarithmic term is proportional to the eigenvalue of the quadratic Casimir operator C2 which is 2 for SU(2) and 3 for SU(3) ( [4] , 18.106). The renormalized coupling constant ( [1] , 20) now reads
 (2)
(2)
which corresponds to ( [4] , 18.133) for C2 = 3 and is used here. The same computations that led to Table 1 in [1] will be repeated here using (2) and with much greater accuracy.
3. Detailed Computation
In the Fortran 77 “dverk” integration subroutine, denote the integration step length by ds. The inter gauge boson distance r that enter the computations is rc = kdds, where kd is the number of steps needed to reach rc. Only at these discrete rc values can the solutions be printed out. This subroutine only allows kd £ 210 = 1024. Since the backward integrations has to start from some large r value, taken to be ≈0.5 GeV-1 in [1] , ds has a minimum dsm = 0.5/1024 ≈ 0.000488 GeV-1. Let rci be the rc closest to ri and rci = kdids. Three step lengths, ds = dsm, 2dsm and 4dsm, corresponding to kdi, kdi/2 and kdi/4, respectively, for a given rci will be used.
A bound state solution exists when the three conditions of ( [1] , 17) is exactly satisfied. This requires that Dmax = 0. Among the three parameters that fix ( [1] , 17), Eb and b0 are continuous and can be specified to any degree of accuracy. But the third parameter ri is according to the last paragraph limited to the discrete rci which can differ from ri by
In [1] , only ds = 2dsm ≈ 0.001 GeV-1 was used. As was mentioned near ( [1] , 18), a criterion for the existence of a bound state solution has been taken to be Dmax < Derr, an error due to the finite integration step length; Derr = ds/rci = 2dsm/rci. As is seen in Table 1 of [1] and Table 1 below, only ri ≈ 0.032 - 0.033 are of interest. In [1] , Derr = 2dsm/ri ≈ 3% and the criterion Dmax < 3% was used. This criterion is not absolute or derivable but is regarded as a plausible first approximation. It is satisfied by the solution ( [1] , 18) with Dmax = 2.69% and the 2 underlined entries in Table 1 of [1] with Dmax = 2.71% and 2.23%.
Here, Derr = dsm/ri ≈ 1.5% and Derr = 4dsm/ri ≈ 6% are also considered. The corresponding criteria are Dmax < Derr ≈ 1.5% and Dmax < Derr ≈ 6%, respectively.
Table 1. This table is the same as Table 1 of [1] with ( [1] , 20) replaced by (2) here to reflect the change of the eigenvalue of the Casimir operator C2 from 2 to 3. Only the underlined two cases satisfy the extrapolated criterion Dmax < Derr ≈ 0.75% below and can be solutions. kdi is the number of integration steps needed to reach rci, the printout rc value nearest to the joint distance ri in ( [1] , 17), for three different integration step lengths, 4dsm, 2dsm and dsm. * denotes that kdi = 60 was excluded due the above kd £ 210 = 1024 limitation in the backward integration.
4. New Results
The computations in [1] are repeated using the more accurate specifications above. The changed results are Dmax = 2.69% → 2.67% in ( [1] , 18), and 2.71% → 2.52% and 2.23% → 1.44% in ( [1] , Table 1). But now the criterion becomes Dmax < 1.5% and is not satisfied by the solution ( [1] , 18) with bare g and MW values and such a bound state no longer exists. Using SU(2) representation, the Lf = 0.30 GeV-1 case in ( [1] , Table 1) with Dmax = 2.71% → 2.52% is also no longer a solution. The Lf = 0.35 GeV-1 case with Dmax = 2.23% → 1.44% is barely < 1.5% but will not survive the extrapolated criterion Derr → 0.75% below.
Now, employ (2) with SU(3) and the more accurate EB, b0 and rci values mentioned above, the results are given in Table 1.
For Lf = 0.20 and 0.30, kdi = 33 and 66 refer to the same rci. Since 33/2 = 16.5 is not an integer, kdi = 17 and 16 refer to this rci + and - 2dsm respectively. It is seen that Dmax is lower for the smallest step length dsm accompanying kdi = 66, as expected. The four cases with kdi = 17, 34 and 68 are accompanied by the step lengths ds = 4dsm, 2dsm and dsm, respectively, correspond to the same rci and yield the same integration results. This shows that the computer accuracy is independent of these step lengths; only printouts do. Extrapolating these cases by reducing ds one more step down to dsm/2, Derr → dsm/2ri. The so-extrapolated criterion becomes Dmax < 0.75% which is satisfied only by the two underlined cases in Table 1. A further reduction leads to Dmax < 0.375% which is only satisfied by the Lf = 0.35 case. If the step length is reduced by half once more, Dmax < 0.1875% and there is no solution for any case in Table 1 and also in Table 2.
The Lf = 0.35 case with Dmax = 0.35% in Table 1 using SU(3) representation is far more close to 0 than does the 2.23% from Table 1 of [1] . It may be regarded as a solution to the bound state and is tentatively assigned to H(125) instead. The calculated mass Eb = 116.845 GeV is much closer to 125.09 GeV [2] than does 110.02 GeV in [1] . The wave functions for these cases are close to that given by the dotted curve in Figure 1 of [1] .
Equation (2) shows that Lf is an infrared cutoff and represents the size of the normalization box for a W± boson. Its mass MW = 80.385 GeV is interpreted to have been determined when this boson is separated from other interacting particles by >Lf. Lf = 0.35 GeV-1 in Table 1 appears to be compatible to some of the experi- mental conditions determining MW. Also, Eb gets closer to the measured 125 GeV with increasing Lf. But why Dmax is small enough for the present bound state to exist only when Lf ≈ 0.35 GeV-1 is not understood.
Table 2. Deviations Dmax for different Casimir operator eigenvalues C2 for Lf = 0.35. The underlined values satisfy the above twice extrapolated criterion Dmax < 0.375%. C2 = 3 for SU(3) is preferred by the bound state.
5. Variation of C2
The calculations leading to Table 1 has been repeated for Lf = 0.35 GeV-1 using different C2 in (2). The results are shown in Table 2.
This table shows that solutions according to the twice extrapolated criterion Dmax < 0.375% exist only for 2.94 £ C2 £ 3.0. The bound state bosons W+W- prefer SU(3) and reject SU(2).
To obtain more precise prediction on the existence of bound state solutions, the Fortran 77’s “dverk” subroutine may be replaced by more modern routines including finite element method.
6. Consequences
If the 2012 H(125) is indeed a bound state W+W, it can no longer be the SM Higgs and at least the low energy end of SM is without foundation and has to be abandoned. No appreciable predictive power is lost; SM has not been able to account for basic hadron spectra and decays. SSI [3] is far more successful in this region. Mass generation of W± comes from pseudoscalar mesons when the relative time between the both quarks in the meson is taken into account.
Further, the presence of a Higgs condensate, disregarding the requirement that its isospin must be >0, will lead to a cosmological impasse ( [5] , p. 247). Such a condensate originated in the hypothesis (Nambu…) that vacuum contains a spin 0 background field that is spontaneously symmetry broken. It is reminiscent of the aether of the late 19th century that permeates the vacuum as a medium carrying light waves. Such attempts to put physics into the vacuum are against the historical examples that new physics come from some basic principles and mathematics ( [3] , Appendix G, Sec. 6). They do not work.
Cite this paper
F. C. Hoh, (2016) Higgs-Like Boson and Bound State of Gauge Bosons W+W- II. Journal of Modern Physics,07,1304-1307. doi: 10.4236/jmp.2016.711115
References
- 1. Hoh, F.C. (2016) Journal of Modern Physics, 7, 36-42.
http://dx.doi.org/10.4236/jmp.2016.71004 - 2. Olive, K.A., et al. (2015) Chinese Physics C, 38, 090001.
http://dx.doi.org/10.1088/1674-1137/38/9/090001 - 3. Hoh, F.C. (2011) Scalar Strong Interaction Hadron Theory. Nova Science Publishers, Hauppauge.
- 4. Lee, T.D. (1981) Particle Physics and an Introduction to Field Theory. Harwood Academic Publisher, New York.
- 5. Wilczek, F. (2005) Nature, 433, 239-247.
http://dx.doi.org/10.1038/nature03281


