Received 21 February 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

The Current Standard Model of the Universe asserts that the universe is generated from a single Big Bang event followed by inflation. There is no center to this universe, hence, no preferential reference frame to describe the motions of celestial objects. We propose a new, Shell Model of the Universe, which contends that the universe is created from multiple, concentric big bangs. Accordingly, that origin presents itself as a unique, preferential reference frame, which furnishes the simplest description of the motions of galaxies in the cosmos. This is similar in manner to how planetary motion is more straightforwardly described via a sun-centered Solar System rather than an earth-centered one. The appeal of the Shell Model of the Universe lies in its simplistic ability to resolve the paradox of quasars, explain the variability in Hubble’s Constant, and solve the problematic accelerated expansion of the universe.

Keywords:

Big Bang, Variability in Hubble’s Constant, Paradox of Quasars, Problematic Accelerated Expansion of the Universe

1. Introduction

1.1. Hubble’s Law and Constant

In 1929, Edwin Hubble discovered a linear relationship between the recession velocities of remote galaxies, , and the distances to those galaxies, d. His findings suggested that our universe was expanding. The relation,

(1)

is known today as Hubble’s Law, where Hubble’s Constant, 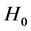, is a measure of the cosmic expansion rate. To obtain a definitive value for, it is necessary to be able to precisely measure and d. Astronomers are capable of accurately calculating a celestial body’s recession velocity by measuring the object’s spectral redshift, z, and utilizing the relativistic Doppler effect relation,

(2)

where z is defined to be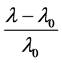, is defined to be the wavelength of a spectral band as measured in the rest

frame, and is defined to be the wavelength of the corresponding spectral band as measured in a moving frame. Determining intergalactic distances has always presented itself as the more difficult challenge, especially when gauging comparatively large ones. However, recent advances in technology, the aid of the Hubble Space Telescope, and the development of new measuring techniques have allowed astronomers to measure distances out to 400 Mpc [1] . Capitalizing on the recent progression, the Hubble Space Telescope Key Project to Measure the Hubble Constant has obtained a value of [2] . Presently, Hubble’s Law stands as one of the fundamental pillars of modern day astrophysics. Roughly 70 years later, this observation is still helping to shape the current theories in astronomy.

1.2. Standard Candle

Spurred by curiosity and concepts from Hubble’s Law, astronomers sought a means of probing into the early expansion history of the universe, which entailed studying relatively distant galaxies. The more remote an object is, the greater the amount of time required for the light to reach us, and thus the further one would be looking back into time. To conduct this probe into the past, it was necessary to find a means of measuring distances to extremely remote galaxies. This could easily be achieved by employing a “standard candle,” which is defined to be any distinguishable class of astronomical objects of known intrinsic brightness that can be defined over a wide distance range [3] . After determining a stellar object’s intrinsic brightness (or luminosity), L, its distance, d, can be straightforwardly calculated using the simple relation,

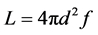(3)

where f is the apparent brightness of the celestial body. The quest to find such a “standard candle” was fulfilled with the suggestion to use the intensely studied type Ia supernovae.

1.3. Expectations

Astronomers jumped at the chance to employ this newly discovered astronomical tool, feverishly searching for distant type Ia supernovae to probe into the universe’s expansion history. By studying remote members of this class of stellar objects, scientists expected to find the expansion rate of the universe to be decreasing over time. Their expectations were largely influenced by the standard model of the universe at that time, which stated that our mass-dominated universe arose following the Big Bang and inflation [3] . Under that model, as time progressed, the mass generated during the birth of the universe should have served to slow the expansion of the universe, a consequence of the attractive, decelerating gravitational effects. Astronomers were hoping to confirm this theory by finding Hubble’s Constant of the past, 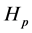, which is related galaxies further away from us, to be greater than Hubble’s Constant of the present, 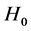, which is related to galaxies closer to us.

1.4. The Search and the Unexpected

After studying a number of distant type Ia supernovae, astronomers discovered these objects to be at greater distances, , than expected given their recession velocities,. This implied that these objects had moved further over time than had been anticipated. After applying Hubble’s Law to their analyses, they discovered Hubble’s Constant of present to be greater than Hubble’s Constant of the past, , signifying an accelerated expansion of the universe over time! This led astronomers to revise the standard model of the universe by the addition of “dark energy,” which presently dominates the decelerating effects of matter and serves to accelerate the expansion of the universe. Currently, the best fitting mathematical models used to simulate the universe show mass energy density to be within a factor of two of “dark energy” density, implying that we are witness to a unique era where the universe is transitioning from matter dominance to “dark energy” dominance. It seems almost unreasonably coincidental that mankind just happened to be studying the expansion of the universe and that technology had advanced just enough to be able to conduct this investigation, during this special transformation period. Many prominent astrophysicists believe this fortuitous set of events signify that there is some fundamental physics that is missing from the Current Standard Model of the Universe [3] .

1.5. Quasar Paradox

In addition to helping shape the Current Standard Model of the Universe, Hubble’s Law also has implications to many other aspects of astronomy. In particular, this simple concept has affected how astronomers view the nature of quasars. Quasars, often referred to as quasi-stellar objects or QSO’s for short, were first discovered in 1963¹. Their most intriguing aspect lies in their enormously high redshifts, which by Hubble’s Law implies that they are receding away from us at extremely high relative velocities. The exceedingly large recession velocities of quasars imply that they are at distances of 5 to 10 billion light years from the earth. Furthermore, the apparent brightness of a QSO at such enormous separations would imply an energy output of 100 times that of the entire Milky Way Galaxy generated by an object roughly the size of our Solar System! There is no simple explanation for these phenomena, and it is proposed that matter falling into very massive black holes is the mechanism whereby such enormous amounts of energy are energy.

1.6. The Shell Model of the Universe

The variations in Hubble’s Constant, the accelerated expansion of the universe, and the tremendous power output of quasars are all explained by the Current Standard Model of the Universe using rather complicated mathematical models. The Shell Model of the Universe was developed to provide a new, alternative framework for interpreting astronomical observations. This unconventional model asserts that the universe is comprised of numerous radially-expanding, concentric, galactic shells, each the result of a big bang. Figure 1, including Figure 1(a) and Figure 1(b), shows that all galaxies residing on the same shell are at a corresponding age. The contention is that our universe is conglomerate of numerous, unequally-matured shells created from multiple big bangs with a common origin and not simply a center-less collection of masses generated by a single Big Bang per the Current Standard Model of the Universe. Figure 1(a) represents the cross-sectional view of the Shell Model of the Universe.

1.7. Valuable Astronomical Observations

In order for the framework provided by the Shell Model of the Universe to be relevant and useful for discussing astronomical phenomena, it must be based on real observations. Because no galaxies observed have exhibited blueshifts, only redshifts, the multiple big bangs must have a common center. One piece of data that is crucial to the construction of this model is the largest observed redshift of, which belongs to a quasar discovered by the Sloan Digital Sky Survey [4] . Based on this information and a couple of simple assumptions, the expansion velocity of the concentric, galactic shells can be calculated to be 0.762c. Other applicable pieces of data emerge from observations that certain aged stars in our galaxy are approximately 12.5 billions years old and that the universe as a whole is roughly 14 billions years of age [5] [6] . This places the age of our galactic shell between 12.5 and 14 billion years. Note that a value of 13.5 billion years will be selected for discussion purposes. Because the universe was confirmed to be flat by evidence from the microwave background radiation [7] , interstellar distances can be gauged using straight lines with no need for non-Euclidean geometry. The Shell Model that will be used to analyze the quasar paradox, the variability of Hubble’s Constant, and the accelerated expansion of the universe will consist of five shells: 1) the shell containing our galaxy, which is at an age of 13.5 billion years, 2) a shell one billion years younger than ours at an age of 12.5 billion years, 3) a shell one billion years older than ours at an age of 14.5 billion years, 4) a shell six billion years younger than ours at an age of 7.5 billion years, and 5) a shell six billion years older than ours at an age of 19.5 billion years (see Figure 1(b)).

2. Constructing a Shell Model of the Universe

For simplicity, this model ignores the decelerating effects of gravitation and assumes that the five galactic shells all have the same, constant radial expansion velocity of.

2.1. Determining the Expansion Velocity of the Universe

This section will outline the methodology used to arrive at a value of for the expansion velocity of the universe. As was mentioned earlier, the largest observed redshift of ² belongs to a quasar. By substituting that value into the aforementioned Doppler relation stated in (2), we can determine that the quasar is receding away from us at the tremendous relative velocity of. Imagine a typical, spherical balloon being inflated. Perceptively, different points on the balloon’s surface will recede from the mouth of the balloon at unequal rates with the end located directly opposite the distention point retreating most rapidly. Of all celestial objects, quasars have the highest relative velocities with respect to us. The Shell Model of the Universe logically places them on the other half of the shell nearly completely opposite the Milky Way. Because all galactic shells are assumed to maintain the same expansion velocity, quasars could hypothetically reside on any of them, the crucial factor being that their movements are oriented in a direction completely opposite ours along the diagonal connecting our galaxy to the center (see Figure 2).

Utilizing this conception, the calculation of the expansion velocity of the galactic shells, i.e. the expansion velocity of the universe, becomes a straightforward task. Figure 3, including Figure 3(a) and Figure 3(b), shows the movements of Milk Way Galaxy and quasars with respect the reference frame located at the center of the big bangs. This computation employs the relativistic velocity transformations, which states that if an inertial reference frame M moves with a velocity of u relative to a reference frame S and an object moves with a velocity of v in S, then this object moves with a velocity of with respect to M, where

(4a)

(4b)

(4c)

In these formulae, u is oriented parallel to (see Figure 3(a)).

In this model, S will designate the reference frame located at the center of the big bangs. M will represent the Milky Way’s (our) reference frame, which travels along the positive x-direction at the expansion velocity of with respect to frame S. Because the aforementioned quasar with the highest redshift has a z-value of 6.4 discovered by the Sloan Digital Sky Survey, we will place this object directly opposite our galaxy. As a consequence, the velocity vector of the quasar with respect to S can be decomposed as follows: (see Figure 3(b)). Making the appropriate substitutions yields the resulting transformation:

(5a)

(5b)

(5c)

Thus, for a relative velocity of, the expansion velocity of the universe can be determined to be. This value will be utilized throughout the remainder of this discussion.

2.2. Determining the Age of the Galactic Shells

In this section, we focus our attention on determining the age and the number of galactic shells, correspondingly, the time in between and abundance of big bangs. Hubble’s Constant, , has been estimated to be between and, but for sake of simplicity a value of will be used. The traditional units used to express Hubble’s Constant can be converted to other units using dimensional analysis to yield an value of. Hubble Time or is often associated with the age of the universe, and a Hubble’s Constant value of translates to an age of approximately 14 billion years. Indeed, other methods have confirmed the age of the universe to be more or less that value [5] . Additionally, the age of old stars in our galaxy have been estimated at 12.5 billion years [6] , which places the age of our Milky Way Galaxy between 12.5 and 14 billion years. For discussion purposes, it would not be unreasonable to approximate the age of the shell containing our galaxy at 13.5 billion years. The other four shells in this working model of the universe were assigned ages of 7.5, 12.5, 14.5, and 19.5 billion years. These numbers have been chosen to provide a wide range of values for analysis. These figures and even the shell count will undoubtedly need to be refined to fit astronomical data, but as a first estimate, they will serve to provide valuable insight. With this, the foundation has been laid to begin construction of a working Shell Model of the Universe.

2.3. Constructing a Working Shell Model of the Universe

The model that will be employed later for discussion purposes asserts that the universe was created 19.5 billion years ago, when the first big bang generated the outermost of the five shells in our universe³. Accompanying the first big bang was the first inflation that sent the mass engendered flying radially outwards at very rapid speeds. As the effects of inflation subsided, the outermost shell settled at the current expansion velocity of.

Five billion years after that first cataclysmic event, another big bang generated the second to the outermost shell. Following a period of inflation, that shell also settled at its current expansion velocity of. This process was repeated again one billion years after the second big bang (six billion years after the first big bang) to produce the shell that would eventually give rise to our Milky Way Galaxy. The second to the innermost and the innermost shells were created by the same processes seven and twelve billion years, respectively, after the first big bang. Finally, 7.5 billion years after the most recent big bang, we arrive at the current state of our universe. All five shells have assumed a constant expansion velocity of following the relatively brief inflationary period that each separately underwent⁴.

Figure 4 depicts the generation of this 5 shelled model of our universe up until its present state. We have made numerous references to the ages of the galactic shells. However, at first glance, there seems to be no inclusion of a dimension in our figures to account for time. Here we contend that, indeed, time can be depicted in a single diagram concurrently with the three dimensions of space. Our assertions are founded upon one guiding principle: movement is the most fundamental quantity/unit; only when we have movement do we have the concepts of time

elapsing and space being occupied [8] . The first big bang generated a sizeable amount of energy in the form of light along with the cosmic mass it created. One of Einstein’s postulates of Special Relativity states that the speed of light is constant. Bearing that in mind along with the simple relation: distance = speed ´ time, then the distance traveled by the light generated during the first big bang is, in essence, a timepiece recording the age of the universe. The expansion velocity of the shells in our model of the universe maintains a one-to-one correspondence with that light by sustaining a constant value of with respect to an observer at the center of the universe. Hence, the distance traveled by the expanding shells can also be used to record the passage of time. It should be recognized that none of the galactic shells have sustained that constant expansion velocity throughout their maturation. This is especially true during inflation, when the expansion speeds far exceed that value [5] . However, the duration of the inflationary periods is comparatively small to the timescale we are working with, which makes the approximation within reason.

3. Interpreting Astronomical Observations Using the Shell Model of the Universe

Now that a working Shell Model of the Universe has been constructed, we will proceed to examine its utility in interpreting astronomical observations.

3.1. Relative Velocity of Galaxy X as a Function of ÐXSM

In the proceeding discussion, we will establish a geometric relationship for determining a galaxy’s relative velocity with respect to us. It may be helpful to make references to Figure 5 throughout this discussion. In this figure, our Milky Way Galaxy is designated by the letter M. Galaxy B lies on the same shell as us, while Galaxies A and C reside on a younger shell one and an older one, respectively. Additionally, Galaxies A, B, and C are all on the same radial vector, such that, and all assumed to expanding radially outward at the expansion rate of the universe, V. To calculate the relative velocity, , of any galaxy X with respect to us, the relativistic velocity transformations are again employed and summarized as follows:

(6a)

(6b)

(6c)

(6d)

As a concrete example, a value of 30˚ will be substituted for along with the previously calculated value for the expansion velocity of. From this, a value of is obtained for. This means that under this given model, all galaxies that form a 30˚ angle with the center of the universe and the Milky Way will be receding from us at a relative velocity of, a value that can be measured from the redshift. Indeed, the relative velocity of any galaxy with respect to our reference frame, remains solely a function of the expansion velocity of the universe and the angle formed by the body, the origin of the big bangs, and our galaxy.

3.2. Location of Galaxy X, Where Light Currently Being Received Was Emitted

To determine the location of Galaxy X, where the light we are currently receiving was emitted from, three general cases must be considered. There is the first case of a galaxy residing on the same shell as ours, the second case

of a galaxy residing on an inner shell with respect to ours, and the third case of a galaxy residing on an outer shell with respect to ours.

3.2.1. Case 1: Galaxy B Resides on the Same Shell as Our Galaxy

This section will draw upon numerous references to Figure 6. In this figure, our Milky Way Galaxy is designated by the letter M and is currently at an age of. Galaxy B, which is on the same shell as our galaxy, is also at an age of. Light presently emitted by B has not yet reach us at M, as light itself has a finite speed and B and M are spacially separated. We are, however, receiving light that is t years old from B′, from a time when Galaxy B was only at an age of. Time is accounted for by placing B’s at a radius of

(7)

and B and M at a radius of

(8)

consistent with principles stating that movement is the most fundamental quantity/unit; only when we have movement, we have the concepts of elapsing and space being occupied, discussed earlier in Section 2.3.

When we take a gander up at the night sky and see Galaxy B, we are not looking at Galaxy B at its present location. Rather, we are looking at Galaxy B of the past and light that is t years old from a time when Galaxy B was still at B′. Thus, when astronomers measure the distance to Galaxy B, they are actually measuring the distance to B′ and not to Galaxy B′s current location, which is presently unobservable. Here we make the distinction that the measured astronomical distances are actually the distances traveled by the light before hitting our eyes or instrument (the light-traveled distances, d) and not the actual distance to the celestial object’s current position. Computing d is straightforward, as it is simply a product of the speed of light and the time traveled by the light, i.e.

. (9)

This concept is extremely important, because it is this the accurate measurement of this value that sparked the search for a standard candle. It was also the employment of this value in calculating Hubble’s Constants of the past and present that led to the conclusion that our universe was undergoing an accelerated expansion.

Another important relation,

(10)

can be derived from this diagram using the law of cosines. Using this formula, we are able to calculate t, given the expansion velocity of the universe, the current age of our shell, and, which will correspond to a particular redshift. After obtaining a value for t, the Cartesian coordinates of B’ can be computed using the following relations.

(11a)

(11b)

As an example, if the age of our shell is, the expansion velocity of the universe is, and the angle formed by the trajectory vectors of Galaxy M and B is, then the time it has taken for the light to reach our eyes from B′ is from a distance of. Hence, in our survey of the sky, Galaxy B appears to be at B′from relation (11a-b) when in reality it has already moved to the position B. In Figure 7(a), the coordinates of B′ were determined for a variety of values and graphed as the blue line.

3.2.2. Case 2: Galaxy A Resides on an Inner Shell with Respect to Ours

It will be helpful to refer to Figure 8 during this portion of the discussion. Our Milky Way Galaxy, designated by the letter M, presently resides in a shell at an age of, while Galaxy A presently belongs to a younger, inner shell at an age of. Our galaxy, M, is presently receiving light emitted by Galaxy A, when it was at the point A′, while the shell containing the galaxy was at an age of. The radius to A′ is

, (12)

and the radius of the shell in which M is located is given by the same relation stated in (8).

Because it has taken the light emitted when Galaxy A was at position A’ a time of t to reach the observer at M, the light-traveled distance is. t can be calculated using a relation derived from the law of cosines:

(13)

Reasonable values for V and have already been established, and can be correlated to the object’s recession velocity. All that remains in solving for t is making reasonable estimates⁵ for T. The coordinates of A' are given by (11a-b).

If, , , and the inner shell that A resides on is younger than our shell, then the time it has taken for the light to reach us from A′ is t = 6.96 Gyr from a distance of d = 6.96 Glyr. This places A′ at the coordinates, although Galaxy A has long since moved to the position. Similar calculations were performed for a number of values and plotted as the green line in Figure 7(a). An identical set of computations were performed for and an array of’s. However, negative values were obtained for t, implying that no light from the 6 billion-year history of this younger shell has yet reached our galaxy.

3.2.3. Case 3: Galaxy C Resides on An Outer Shell with Respect to Ours

In this final case under consideration, it would be informative to refer to Figure 9. Again, our Milky Way Galaxy is designated by the letter M and presently resides on a shell at the age of, while Galaxy C presently belongs to an older, outer shell at an age of. Our galaxy is currently receiving light that is t years old from C′, from a time when Galaxy C was at an age of. Time is denoted by placing C′ at a radius of

(14)

and M at a radius given by (8).

It has taken the light emitted by Galaxy C when it was at C′ a total of t years to reach an observer at M. Hence,

the distance from M to C′ is, again, simply. Similar to the other two cases, a law of cosines relation:

(15)

can be derived to solve for t. Again, values for the expansion velocity of the universe (V) and the age of our shell () have already been reasonably determined, all that remains to solve for t is inputting appropriate values for T for a broad range of’s.

For example, if, , , and the outer shell that C resides on is older than our shell, then the time it has taken for the light to reach us from C’ is from a distance of. Although Galaxy C is now currently at the position , we perceive it to be at C’. Similarly calculated values were obtained for a variety of’s and diagramed as the red line in Figure 7(a). The magenta line in this figure represents similar computations performed for an outer shell older than ours.

Assuming that our universe can be modeled by a Shell Model of the Universe consisting of five shells: 1) the shell containing our galaxy, which is at an age of 13.5 billion years, 2) a shell one billion years younger than ours at an age of 12.5 billion years, 3) a shell one billion years older than ours at an age of 14.5 billion years, 4) a shell six billion years younger than ours at an age of 7.5 billion years, and 6) a shell six billion years younger than ours at an age of 19.5 billion years, Figure 7(a) represents the universe as presently seen by us, here in the Milky Way. This is to be contrasted with the actual state of the universe shown in Figure 7(b), which is from the vantage point of an observer sitting at the center of the big bangs, taking a record of motions of objects in the universe. Notice that from our perspective, we are unaware of the existence of the innermost galactic shell, whose light has yet to reach our eyes.

3.3. Hubble’s Law and the Ratio of

The previous sections provided us with the means of constructing a view of the universe based our limited, historically-based perspective (see Figure 7(a)). Additionally, it furnished us with the tools necessary to take a closer look at Hubble’s Law and the ratio of. Assuming the expansion velocity of the universe to be a constant, it was shown in relation (6a-d) that the relative velocity of any galaxy with respect to our reference frame, remains solely function of the angle, , formed between the velocity vectors of that galaxy and ours. Thus, assuming no change in the expansion rate, the relative velocity of all galaxies with respect to us should remain the same, because the angle formed by the velocity vectors does not change.

Additionally, we derived methods for determining the light-traveled distance, , which is the distance that astronomers are interested in measuring using standard candles, by examining the following three cases: 1) the light source is from a galaxy that presently resides on the same shell as us, 2) the light source is from a galaxy that presently resides on an inner shell relative to ours, and 3) the light source is from a galaxy that presently resides on an outer shell relative to ours. To solve for t, we employ the law of cosines relations stated in Equations (10), (13) and (15) respectively, for the three cases.

Suppose Galaxies A, B, and C are all expanding along the same line, such that their trajectory vectors make a 30 degree angle, , with our velocity vector. With respect to our galactic shell, Galaxy A presently resides on an inner shell and Galaxy B resides on the same shell, while Galaxy C resides on an outer shell (see Figure 5). The age difference between our shell and the inner and outer shells is 1 billion years, i.e.. Using the previously calculated values for expansion velocity of the universe, , and the age of our shell, t₀ = 13.5 Gyr, we can arrive at and compare the ratio of for the three cases. There are the first case of galaxy B residing on the same shell as our galaxy, the second case of galaxy A residing on an inner shell with respect ours, and galaxy C residing on an out shell with respect to ours. Because is the same for Galaxies A, B, and C, the recession velocities of these galaxies are all.

3.3.1. Case 1: Galaxy B, which Presently Resides on the Same Shell as Our Galaxy

Solving the first law of cosines Equation (10) for t and multiplying by c, we obtain a value of, which means that the source of light is 6.09 Glyr away. Dividing this galaxy’s recession velocity of by this d value, we obtain a ratio of

(16)

for Galaxy B at B′.

3.3.2. Case 2: Galaxy A, Which Presently Resides on An Inner Shell Relative to Our Galaxy

By solving for t in (13) and multiplying by the speed of light, we calculate the light-traveled distance to be. This corresponds to

(17)

for Galaxy A at A′.

3.3.3. Case 3: Galaxy C, Which Presently Resides on An Outer Shell Relative to Our Galaxy

Similarly, by deriving t from Equation (15) and multiplying by c, we arrive at a value of. Dividing the previously calculated value of by d, we obtain a ratio of

(18)

for Galaxy C at C′.

Because the recession velocity for all three of these galaxies is the same, the only factor in the variability of is the distance, d. There is trend in the ratios of, i.e. “Hubble’s Constant,” with those galaxies furthest away

yielding the smallest values and those at the closest proximity producing the largest numbers. These results imply that as we look further and further back into time, i.e. we look at more and more distant galaxies, “Hubble’s

Constant” decreases. Thus, as the universe has aged, the ratio of has increased. Under the Current Standard

Model of the Universe, the resulting increasing progressing in “Hubble’s Constant” with the passage of time implies an accelerated expansion of the universe. The ever elusive dark energy is purported to be the driving force behind this increase. However, throughout this discussion and the history of the Shell Model of the Universe, it has been assumed that the expansion velocity of the universe has remained a constant,. Thus, the varia-

tion in the ratio of can be attributed to the model under which the astronomical phenomena are interpreted.

Dark energy has no place in this new model.

The appeal to this new Shell Model of the Universe over the Current Standard Model of the Universe lies in its simplicity and its ability to straightforwardly address the quasar paradox, the variation in “Hubble’s Constant,” and the purported accelerated expansion of the universe. Consideration of this new model would seriously call to question not only the current model but more fundamentally, Hubble’s Law. Just from the example above, we see that there is no one-to-one correspondence between and d, as stated by “Hubble’s Relation”:. Undoubtedly, this new Shell Model of the Universe requires refinement. However, as a rough first model, it provides invaluable insight and seriously challenges current prevailing theories. For instance, the enormously large redshifts of quasars are a result of their orientation with respect to us and are not at the extensive distances implied by “Hubble’s Law.” Because those phenomena are not as far away as previously imagined, there is no enormous energy output to explain by matter falling into black holes.

4. Predictions of the Shell Model of the Universe

A useful model should not only be able to explain current phenomena but should also be able to make predictions.

4.1. Youngest, Hypothetical, Visible Shell

Previously, in Figure 7(a), it was shown that we are not able to see galaxies on an inner shell that is 6 billion years

younger than ours. We cannot calculate a ratio for from an inner shell at an age 7.5 billion years, because we

cannot gather data from things we cannot see. In the subsequent discussion, we will calculate where that cutoff is, i.e. what is the youngest a shell can be for us to be able to see it. Looking at Figure 8, two properties should be satisfied by this hypothetical inner shell: 1) the light that is just reaching us shows the shell right as it is being born, i.e.

(19)

and 2) that light has traveled the distance that we are from the origin of the multiple big bangs, i.e.

(20)

From equations (8) and (9), we saw that and, respectively. Hence, by substitution, we find that

. (21)

In our current working model and, therefore, we find that. Thus, we are only able to see a hypothetical shell that is younger than ours by a maximum of 3.2 billion years. The unobservable mass in younger shells could explain some of the lost mass necessary to reach the critical density for the Big Crunch. Likewise, if the galaxies in outer shells of our universe have died a very long time ago, we may also be unable to see them, because the last of the light they emitted has already passed us by, but they will still contributors, adding to the density required for the Big Crunch. Furthermore, additional mass could potentially be generated with more and more big bangs.

4.2. Maximal Redshift Value That Cannot Be Exceeded by Objects in Line of Sight

The final prediction that will be discussed will utilize Figure 10. The line connecting our galaxy M to the origin of the big bangs will be designated as the x-axis. Our mathematical model predicts that for any angle, we may

observe galaxies with redshifts less that or equal to but no larger than, where

(22)

and is given by (6a-d). It was proved earlier that recession velocity and analogously, redshifts, are only functions of the expansion velocity V and. Thus, with a value for V determined, this relation is true, because the upper ray of never intersects with the upper ray of. This ray only intersects with the rays of angles less than, which corresponds to redshift values less than. This means that if you observe the cosmos at a particular line of sight, , you should never see a galaxy with a redshift higher than. On a similar note under this Shell Model of the Universe, high redshift objects, i.e. quasars, should all be clustered around the same patch of sky, at.

5. Conclusion

This new Shell Model of the Universe has been constructed to provide simpler explanations to astronomical phenomena. This model has parsimoniously addressed the quasar paradox, the variability of “Hubble’s Constant,” and the purported accelerated expansion of the universe, something which the Current Standard Model of the Universe has had limited success with. In science, Ockham’s Razor reigns supreme.

Cite this paper

Tower Chen,Zeon Chen, (2016) The Shell Model of the Universe: A Universe Generated from Multiple Big Bangs. Journal of Modern Physics,07,611-626. doi: 10.4236/jmp.2016.77062

References

NOTES

^*Corresponding author.

¹The terms QSO’s and quasars are used interchangeably here. It should be noted that some astronomers define quasars, i.e. quasi-stellar radio sources, to be the radio emitting subset of QSO’s. Semantics should not be the focus.

²An even higher value may have been observed recently or maybe be observed in the future, but the conceptual basis for this calculation remains the same.

³Again, it should be recognized that this is an incomplete model that should be subjected to further refinement. Nevertheless, as a working model, it provides ripe ground for discussion.

⁴Again, for simplicity, the effects of gravity are not factored in. They should be considered in more refined versions of this model.

⁵Fitting values to actual data should provide better estimates for T.