Journal of Modern Physics
Vol.06 No.15(2015), Article ID:61794,20 pages
10.4236/jmp.2015.615220
The Ni’s Solution for Neutron Star and Outward Oriented Gravitational Attraction in Its Interior
Luboš Neslušan
Astronomical Institute, Slovak Academy of Sciences, Tatranska Lomnica, Slovakia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 2 October 2015; accepted 6 December 2015; published 9 December 2015

ABSTRACT
In 2011, Jun Ni published the solution of the Tolman-Oppenheimer-Volkoff equations describing the structure of stable neutron stars, which implies that 1) there is no upper mass limit of these objects, 2) their outer physical surface is always situated above the corresponding event horizon, and 3) the object is a hollow sphere with the inner physical surface and cavity inside. In our paper, we propose to “purify” the general relativity, as the geometrical theory, from the concept of mass. If we get rid of the concept of mass and Newtonian-type potential, then we obtain such the behavior of gravity which results in the above mentioned stable Ni’s object. It is farther pointed out that the distribution of matter, which is observed as spherically symmetric by the observer in its center, is not longer observed as spherically symmetric by an observer aside the center in a curved spacetime of general relativity. This fact implies, in contrast to the Newtonian physics, the non- zero and outward oriented gravitational attraction of upper layers of star. Ni considered positive energy density and pressure. In addition, gravity had everywhere attractive character. No “exotic” assumption was made. Hence, there is no reason why his concept of hollow sphere should not be applicable to the models of real objects.
Keywords:
Relativistic Compact Objects, Neutron Stars, General Relativity, Ni’s Solution

1. Introduction
In their famous work published in 1939, Oppenheimer and Volkoff [1] concluded that there is no solution for a stable configuration of dead star, without an internal source of energy, if the mass of the star exceeds a certain critical limit, which was later named by them. In the subsequent work, it was demonstrated that the star has to collapse below its event horizon [2] .
The conclusion about the non-existence of the stable configuration of very massive stars and the necessity of their collapse to become the black holes has been regarded as valid more than three quarters of century and is hard to believe that something could ever bring a doubt about this claim. In 2011, Chinese researcher Jun Ni [3] however published a solution, which forces us to deal again with the question on the stable configuration of very massive stars. Ni attempted to reproduce the creation of the Oppenheimer-Volkoff model of neutron star. He proceeded in the same way as the original authors of the model, except of the starting point of the numerical integration of the differential equations, which are relevant to the model. While Oppenheimer and Volkoff started the integration in the center of the object, Ni started it in a finite star-centric distance.
The inward proceeded part of the Ni’s integration always ended with zero pressure and energy density in a finite star-centric distance, i.e. he obtained a model with an inner physical surface of the object. In addition, he concluded that there is no upper-mass limit. And, the outer physical surface appears to be always situated above the corresponding event horizon.
In this paper, we attempt to analyze the reason why Ni was successful in the creation of the stable model for very massive compact object. Clearly, the Ni’s result evokes some fundamental questions on the principles and postulates within the general relativity, especially those, which were originally established within the Newtonian physics and appeared in general relativity after their formal generalization.
2. TOV Model of Neutron Star
2.1. The Original Basic Equations
The first model of the star that spent all its storage of nuclear fuel was worked out for the spherically symmetric, non-rotating objects by Oppenheimer and Volkoff [1] . They used the description of gravity almost simultaneously published by Tolman [4] . Hence, this kind of model is named as the Tolman-Oppenheimer-Volkoff or TOV model. This model includes the equation of state (EoS, hereinafter) published by Chandrasekhar [5] who derived this EoS considering some ideas from the previous work by Landau [6] . The Chandrasekhar’s EoS describes the state of a pure neutron, extremely cold and, thus, degenerated gas. Hence, the objects of this kind started to be named as neutron stars (NSs), although there are known, today, also their models consisting of a more complex, not only neutron, matter.
To describe the gravity, Tolman [4] considered the Einstein field equations (EFEs) [7] [8] . He simplified these equations for the case of spherical symmetry. (The EFEs for the spherical symmetry were already published by Eddington [9] earlier. Tolman specified more some details.)
In our paper, we also aim to construct the TOV simple model of non-rotating and, therefore, spherically symmetric NS. So, we use the already mentioned form of the EFEs for the spherical symmetry explicitly given by Eddington [9] and Tolman [4] . We remind these equations:
 (1)
(1)
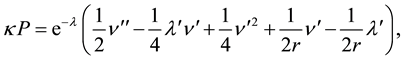 (2)
(2)
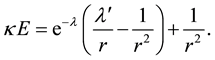 (3)
(3)
The meaning of used symbols is following. P is the pressure, E is the energy density, and
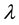 and
and
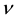 are the auxiliary functions related to the components of metric tensor
are the auxiliary functions related to the components of metric tensor
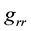 and
and
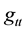 as
as
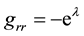 and
and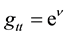 . In the static case,
. In the static case,
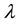 and
and
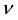 are only the functions of the star-centric radial distance r. The prime indicates the derivative with respect to r. Because of a better transparency we need in our explanations, the equations are given in the form assuming the usage of the SI units. In this system of units, constant
are only the functions of the star-centric radial distance r. The prime indicates the derivative with respect to r. Because of a better transparency we need in our explanations, the equations are given in the form assuming the usage of the SI units. In this system of units, constant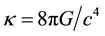 , where G is the gravitational constant and c is the speed of light. Using Equations (1)-(3), it is possible to derive the equation for the gradient of pressure balancing the gravity in the form
, where G is the gravitational constant and c is the speed of light. Using Equations (1)-(3), it is possible to derive the equation for the gradient of pressure balancing the gravity in the form
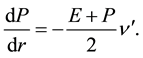 (4)
(4)
Oppenheimer and Volkoff [1] replaced function
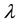 by another auxiliary function, u, defined by
by another auxiliary function, u, defined by
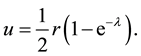 (5)
(5)
Subsequently, the gradient of pressure can be given in the form

To describe the internal state of gas we also use the EoS of the cold Fermi-Dirac neutron gas, which was found by Chandrasekhar [5] . According to this equation, the energy density and pressure equal


where constant






Using the functions




For energy density and pressure given by relations (7) and (8), quantity





where

According to the Birkhoff theorem [10] , the metrics of vacuum in a vicinity of an arbitrary, but spherically symmetric distribution of matter is described by the solution of the EFEs, which was found by Schwarzschild [11] and is well-known as the outer Schwarzschild solution (OSS). The Birkhoff theorem must be also valid in the exterior of each spherically symmetric NS. In the physical surface of NS, the metrics found as the solution of Equations (11)-(13), i.e. the interior metrics, must be smoothly tailored to the metrics described by the OSS, i.e. the exterior metrics.
In the following, let us outline the derivation of the OSS from the Equation (12) and Equation (13) written with the help of auxiliary quantity u. In the vacuum in a vicinity of NS body, there is everywhere valid that






For v and

which can be analytically integrated. The integration yields

where



We denoted
Integration of Equations (11)-(13) for the stellar interior yields the values of quantities u (then





















Relation (14), which is valid inside the NS body (







The metrics in the physical surfaces of NS is actually continuous, if not only interior and exterior




in the outer surface and analogous conditions have to also be obeyed in the inner surface.
In a large distance from the NS, the gravitational field is weak and we expect its convergence to that described by the Newtonian physics. It is known that this demand is obeyed when



We further remind that the rest mass (sum of the rest masses of all neutrons constituting the object),


where


Because of relations (7) and (8), the maximum energy density and maximum pressure occur in the same distance as the maximum of auxiliary function




Analyzing relation (11), the condition







2.2. Some Constraints in the Traditional Representation
It appears that the Ni’s hollow-sphere model of NS can be constructed after ignoring some constraints, which are demanded, explicitly or implicitly, according to the traditional concept of compact objects. Below, we briefly point out to these constraints.
The demand, that the metrics of vacuum in a vicinity of spherical distribution of matter must be that given by the OSS, yields






A consequence of postulate P1 is that the non-rotating NS must be a full sphere, without any inner physical surface. If there was such a surface and postulate P1 valid, the metrics could not be continuous in the radius of this spherical surface,
Postulate P2 has never be explicitly stated in the literature. It was implicitly established by Oppenheimer and Volkoff [1] , when they started the numerical integration to construct the first NS models from the center of the object. Such the processing is possible only if the mass of the star is distributed down to the center and this is possible only if the gravity is oriented inward in the entire stellar interior.
The Ni’s solution of TOV equations is possible if the postulates P1 and P2 are abolished. In the following sections, we try, beside other, to provide a reason for their abolition within the GR.
3. An Example of Neutron-Star Model Constructed by Using the Ni’s Solution
In this section, let us introduce the basic properties of the NS model constructed by using the Ni’s solution of Equations (11)-(13) in more detail. We numerically integrate these equations starting, for example, in the star-centric distance 10 km. We identify this distance to the distance







The input value of auxiliary function



The behaviors of density (calculated as the ratio of







The metrics in the external vacuum is described by relations (15) and (18) with








Figure 1. The behavior of the density (plot a), components



In Figure 1, one can see that this metrics is perfectly tailored with that valid for the NS’s interior. It means that the metrics is perfectly continuous in both outer and inner physical surfaces. Not only the values of


The negative derivative of



The stable configuration of matter in the interval from






4. Spherical Symmetry and Gravity of Outer Layers
In course to explain the outward acting gravitational attraction, let us, firstly, to deal with an important consequence of spherical symmetry in the Newtonian physics. In this theory, the space is Euclidean regardless the amount, compactness, and radial distribution of matter in the spherically symmetric object. Every such the object can then be divided into a large number of thin concentric material layers. The net gravitational force from every layer can be calculated separately and the total net force is simply the sum of the partial forces from every layer.
Let us consider an infinitesimally small material element of a thin, spherically symmetric layer in a distance









In other words, the force from the element in the given direction is eliminated by the force from the element in the opposite direction. For every element, it is possible to find the element in the opposite direction, exactly eliminating the force of the first element, therefore the total net gravity of the thin spherical layer on the test particle wherever inside it is exactly zero. Consequently, there can be whatever number of outer concentric layers, with the radii larger than the object-centric distance of given test particle, their net gravitational force is the sum of zeros and, hence, zero.
However, it is important to realize that this calculation, with zero result, can be made only in the Euclidean space of Newtonian physics. Only in this case, it can be exactly and generally proved (analytically calculated) that the net gravity of the outer layers of spherically symmetric object is zero.
If we consider a curved spacetime or curved space in a static problem in the GR, there occur two differences, which yield problems. At first, the GR is not linear, therefore we cannot divide any spherical object into a number of thin concentric layers, calculate their partial gravitational actions separately, and obtain the net action by adding the partial results. At second, the distribution of matter, which is seen as spherically symmetric by the observer in its center, is not longer seen, in general, as spherically symmetric by an observer aside the center. The curved space changes the distance to a material element when seen by the observers in different places, in general.
In a calculation of gravitational acceleration of a test particle inside a spherical layer, the element volume is not longer proportional to the quadrate of distance in the curved space. And, the gravitational acceleration cannot be expected to be reciprocally proportional to this quadrate, either. Unless the gravity of outer layers is postulated to be zero, it cannot be expected to be zero, except of some special cases, perhaps. The Ni’s solution implies that this gravity is actually non-zero and oriented outward from the center of the object, which is seen as spherically symmetric by the observer in its center.
5. Analysis of Gravitational Potential
The EFEs are solved via integrations, which produce the integration constants. In an application of the solution of EFEs to a real object, we need to physically represent these constants and find their values. In this process, the fact that the GR must converge to its Newtonian approximation in the limit of weak field was utilized.
Sometimes, it seems that the representations of both these theories are not distinguished, properly. The rules being valid within the classical Newtonian physics are used in an argumentation within GR. Consequently, the GR is, in fact, constrained by these rules if one requires their validity in both theories. Below, we discuss this problem in more detail in the context of the Ni’s solution and demonstrate the consequences in the case when the GR is completely deliberated from the Newtonian physics, in this case. It appears that the most important quantity in this discussion is the gravitational potential, its understanding and definition.
5.1. Potential in Newtonian Physics
When we speak about the gauging of the constants produced by the integrations of the EFEs, the most common example is, likely, the gauging of the constants in the OSS, which describes the vacuum metrics shaped by a point-like particle. This metrics is identical to the metrics of vacuum above the outer surface of the spherically symmetric object. From the integration of the corresponding EFEs, we obtained the components of metric tensor











In the limit of weak field, the gravitational acceleration of a test particle is oriented toward the center of the acting object and, therefore, toward the origin of the coordinate frame considered. In this limit, it is calculated as (e.g., [13] )

Sign minus respects the fact that gravity is attractive force and the acceleration is oriented against the direction of coordinate r-axis. The analogous formula in the Newtonian physics is

in the considered radial case.



This is the “classical” gauging, which implies that there must always be valid


We know that






In the classical Newtonian physics, the gravitational potential used to be defined as the negative of the integral of corresponding gravitational acceleration from a given radial distance r to infinity. In the inverse calculation, the acceleration is calculated as the negative of the gradient of potential. Because the reference point in infinity is the matter of convention, some authors prefer to consider rather a change of the potential when a test particle is moved from a point of space to other point. So, they define the change of potential, which is related to the corresponding change in the potential energy of the particle. This definition is unique, no reference point is necessary.
For example, if the test particle is ejected radially outward from the surface of spherically symmetric object, having its upper radius





5.2. Two Concepts of Potential in General Relativity
To describe the motion of a test particle moving in the vacuum in the static spacetime shaped by a stable concentration of matter, the so-called “effective potential”,
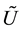



In the metrics described by the OSS, the effective potential is given as



On the other-hand side, we used, in the previous section, the classical Newtonian potential to gauge the auxiliary metric and, therefore, GR quantity u. Thus, this is the second potential sometimes figuring in the GR as the ordinary quantity.
There is no problem, if this is done only in the weak field (and
Notice that while there is demanded


nian potential,


The effective potential was established for the vacuum outside the material object. To generalize the effective potential for whole space, i.e. from r = 0 to infinity, in the case of the Ni’s model of NS, we establish a new gauging of the constant term of this quantity. So, let us now to repeat the well-known derivation of the GR effective potential using the definition that the potential is the integral of corresponding gravitational acceleration. Thus, the first task is the determination of the acceleration. We again consider the spherical coordinate system, r,



The four-vector of acceleration is related to the metrics as

where







Further, we consider exclusively the radial acceleration of a static test particle. It means,


Hence, relation (36) can be simplified and four-acceleration can be given as

Of the Christoffel symbols




Therefore, only the component





The corresponding gravitational potential is integral of this quantity. In the integration, we have to remember the GR contraction of length and, thus, to integrate through the proper element of length
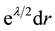

5.3. New GR Gravitational Potential
The potential energy is the negative of the work done against the gravity. In a full-sphere object with the gravitational action everywhere oriented inward, the force to do the work has to be oriented outward. When we calculate the change of the potential energy, the integration is made from a point nearer to the full-sphere object center to a point, which is in a larger distance.
In a hollow-sphere object, the above mentioned direction of the integration to calculate the potential energy and corresponding potential is relevant only in the interval of radial distance from


If one wishes to give a reference point for the calculation of potential generated by hollow-sphere object, the most appropriate is a point just in distance



If








If








In the last formula, term





of view, because it disappears, when we calculate a difference of potential in two points. We know that there is also a difference in the constant term between the Newtonian potential,





The behavior of the new potential in the example of Ni’s hollow sphere presented is Section 3 is shown in Figure 2. We can observe that it acquires only positive values in the entire interval of radial distance (and zero in
To establish the new potential, which is mathematically expressed by Formula (41), we propose to rule out the physical quantity “mass” from the GR and regard the quantity u, established originally by Oppenheimer and Volkoff [1] , as only an auxiliary metric quantity. In accord with its original definition (see relation (5)), this quantity replaces the auxiliary metric quantity



If we regard the negative values of u as physically acceptable, we accept, in fact, that the size of

of metric tensor,

equality

Figure 2. The behavior of the newly defined gravitational potential in the GR in the example of the Ni’s hollow sphere presented in Section 3. The blue thick solid curve shows the potential inside the object’s body. This potential is calculated within the numerical integration of the EFEs by using relation (41). The dashed green (dashed violet) curves shows the potential in the region of radial distance


Within the GR, the concepts of energy (of all kinds) and potential remain. Since it has been empirically found that constant

When the quantity u is regarded as the auxiliary quantity characterizing the metrics, the new gravitational potential can be proved as always positive quantity, even in the region where
5.4. Remarks Concerning the Mass Elimination
To support our suggestion from the previous subsection about the ruling out the mass as the physical quantity from the GR, we remind the suggestion, published in our earlier paper (arXiv: 1206.0405v1 [physics.gen-ph]), to eliminate not only the mass from the physics, but the electric charge and some fundamental physical constants as well.
We know, the fundamental laws, like the Newton force law, Coulomb law, or law of inertia, can exclusively be experimentally verified in a combination of one, e.g. Newton, force law and the law of inertia. In other words, we can verify the prediction made by the solution of the corresponding equation of motion. So, the real physical theory is never represented by a single law, but by an equation (or a set of equations).
Let us explain the principle of the application of fundamental physical laws in the example of two electrically charged, static particles. In this example, the laws are used to describe their dynamics. We determine the acceleration of the first, “test” particle (TP), when influenced by the second, “acting” particle (AP). The TP has mass





where



We assume that the AP and TP are composed of matter consisting only of elementary particles of k kinds, whereby the mass of j-th kind is






Further, if the AP consists of










The dimensional analysis enables combining the fundamental physical constants to obtain special length, time, and mass, which are known as the Planck length,




where




In quantum physics, a wave is associated to every elementary particle. The angular frequency,




If we use this relation to convert masses


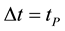

In the last term, the fraction





We can see that the last equation is dimensionless and the fundamental constants G,


The fundamental equations yielding the TOV model (11)-(13) can also be re-written to the dimensionless form. If we denote the wavelength of the wave associated with neutron by









Because this is the static problem, the equations contain only the ratios of lengths and derivatives with respect to length.
The GR was originally intended to be formulated as a geometric theory and Equation (49) as well as Equations (50)-(52) indicate the way toward the GR as the pure geometric theory. Mass does not seem to be any component of such a theory. Hence, our proposal to rule out this quantity from any GR description and argumentation appears to be reasonable.
We note that such the units as meter, second, or kilogram were defined by man and, thus, cannot be regarded as the “natural” physical units. As well, the quantities as mass or electric charge, which were also established by man, can be, in fact, only the artificial quantities not really existing in the nature. Instead, the quantities as length, frequency, their change, and change of their change seem to be natural. And, concerning the physical units, the above mentioned Planck length, Planck time, and speed of light are, likely, the “natural” units.
In the two schematic examples presented above, we could see that if the man-established quantities are replaced by the natural quantities, expressed in the natural units (with the help of Planck length and speed of light) then the fundamental constants, as the gravitational constant, permittivity of vacuum, and Planck constant, simply disappear from the equations describing a physical problem. This circumstance implies that these constants are, most probably, only the transformation constants between the artificial, man-established and natural quantities.
6. Full-Sphere versus Hollow-Sphere Models
In practice, every inward-proceeded part of the numerical integration of Equations (11)-(13), when it is started in a distance larger than zero, ends with the implication of the inner physical surface. (In principle, the numerical integration from a finite distance can end in the center with finite energy density and pressure. This is, however, only a single of infinite variety of possibilities. If there is no special attention to the choice of initial conditions, the probability of its occurrence approaches zero.) Such the property can be also expected for some other equations of state, not only the Chandrasekhar’s Equation (7) and Equation (8). (Actually, the same qualitative behavior occurs using, e.g., the polytrope. And, the energy-density and pressure maximum in a finite distance also occurs for the equation state of radiation,
The realistic solution of the Equations (11)-(13) in the TOV problem has to satisfy the following demands. The pressure and energy density inside the object must acquire only finite positive values and have to decrease to zero at the object’s physical surface. In the full-sphere model, these quantities must be finite in the center. The last requirement implies the asymptotic behavior

















When


















We note that a difference between the full-sphere and hollow-sphere models can be practically negligible. In Figure 3, there is an example of such two similar models. In the hollow-sphere model, the distance of zero net gravity,




Since



We can conclude that the border between the traditionally unacceptable and acceptable models seems to be only formal: the model with exactly zero


7. A Wider Variety of the Ni’s Models of Neutron Stars
In this section, we introduce several sequences of the NS models constructed by using the Ni’s solution of the TOV equations in course to map some properties of them. To obtain the models, we again start the numerical integration of Equations (11)-(13) in the distance of zero net gravity,



Figure 3. The comparison of almost identical TOV full-sphere and Ni’s hollow-sphere models of NS. The top, middle, and bottom plots show the behavior of density, component

we integrate the sequence of models considering the series of input values of Fermi impulse from 0.2 to


The result for some considered values of

Figure 4. The size of NSs of various mass. Each pair of circles linked with a solid horizontal line shows the position of inner (left circle),



distance
For a relatively small value of







For a relatively large value of








Using the Ni’s solution, it appears that there is a variety of NSs constituted by the same number of neutrons. In other words, we can construct a variety of models for a given rest mass, but with the different other characteristics. In Table 1, we present several such the models for the NS with the same rest mass as in the example shown in Figure 3. This rest mass is


8. On the Central Singularity
In the past astrophysical applications of GR, there was well-known the existence of the true singularity in the center of black hole. Because this singularity was situated below the event horizon, it was regarded as having no concern to any observer residing in our universe, i.e. outside of the black hole. Because of this reason, there is the convention that this kind of singularity is not problematic and the metrics containing it can be accepted for a description of real objects. (The singularity is not “naked” singularity.)
On contrary, some solutions of the EFEs yield a true singularity that is not situated inside the event horizon and that can be, in principle, “experienced” by an observer. This kind of singularity is known as the “naked singularity” and its acceptability in a realistic description was ruled out by so-called “cosmic censorship” theorem [16] . According to the latter, no naked singularity, other than the Big-Bang singularity, can exist in the universe and, hence, in the theory, when all the considered conditions are realistic. We note, the naked singularity, other
Table 1. Some characteristics of the models of NSs consisting of the same number of neutrons, i.e. with the same rest mass,
than that of Big-Bang type, would cause a collapse of matter into a point in the center, in which the density would increase above all limits.
In the model of NS based on the Ni’s solution, the metrics inside the internal cavity, which is bordered by the sphere of radius




We note, there is not, either, the local Lorentz frame in the central point, with
It was empirically found that always













Since it is found that the outer radius is always larger than the Schwarzschild gravitational radius and all components of metric tensor are continuous (and everywhere finite) functions of radial distance in every distance
Since the Ni’s solution implies the models of compact objects without any singularity other than the above-mentioned Big-Bang type singularity, it enables us to accept a more strict than the original cosmic censorship. Specifically, we can demand that “no singularity other than the Big-Bang type singularity can exist in the universe and, hence, in the theory, when all the considered conditions are realistic”. It means that adjective “naked” can be omitted in the theorem.
In conclusion, the main reason to postulate the Minkowski metrics in the vacuum inside a spherical shell is abolished in the Ni’s concept of hollow sphere.
9. Conclusion Remarks
The GR was originally created as the geometric theory. Since the geometry of spacetime is determined by stress-energy tensor, the quantities as energy and (effective) gravitational potential are the integral part of the theory, except of the geometrical aspects.
Meanwhile, an alternative to the original intent of truly geometrical theory started to be used, especially in the theory of NSs: the concept of mass within the Newtonian concept of potential was regarded as the integral part of the GR. This concept of the potential differs from the approximation of the GR effective potential for a weak field by an absence of constant term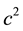

Consequently, the traditional model of spherically symmetric NS, as firstly found by Oppenheimer and Volkoff [1] , is only the single of infinite variety of realistic NS models in GR. A further, infinite set of models appears when we permit that the size of the

In the Euclidean space of Newtonian physics, the net gravity of upper layers is proved to be exactly zero in the case of spherical symmetry. However, the conception of spherical symmetry in the curved spacetime of GR is more complicated. A concentric layer, which is observed as spherically symmetric by the observer in the stellar center, is not longer observed, in general, as spherically symmetric by an observer aside the center. Hence, its gravitational action on a particle situated inside the layer but aside its center is generally non-zero. The solution of the EFEs found by Ni [3] implies that it is actually finite and oriented outward from the center.
Inside the NS, the outward oriented net gravity of upper layers increases with the decreasing radial distance, since the mass of upper layers increases. The behavior of net gravity of lower layers is opposite, of course. In the NS’s interior, there is a critical distance in which the partial gravitational actions of both upper and lower layers equal each other. Below this distance, the net gravity of upper layers becomes dominant and, thus, the total net gravity is oriented outward. In the stable configuration, this gravity is again balanced by the gradient of pressure, which is always oriented against the gravity, according to the equation for the gradient derived from the EFEs. The inner physical surface is formed by the same mechanism as the outer surface.
So, the NS model constructed by using the Ni’s solution of the EFEs is the hollow sphere with a cavity in its interior. The existence of this cavity is enabled by the fact that the metrics inside it is again described by the OSS, but with sign plus in front of the fraction

The negative values of u become physically acceptable, when this quantity is no longer represented in the term of Newtonian-type gravitational potential, but is simply regarded as the metric quantity (alternative form of



The concept of hollow sphere is able, as already claimed by Ni [3] , to create a model of stable compact object of whatever large mass. Such that the conclusion can seem to be in a contradiction with that by Oppenheimer and Snyder [2] who described the collapse of every compact object with a mass larger than a certain upper limit. As well, it contradicts to the conclusion published by Rhoades and Ruffini [17] about the maximum mass of NSs. These works were, however, implicitly based on postulate that the total net gravity must be oriented inward inside the whole NS. Thus, they are valid only for the full-sphere concept of NS.
With the concept of hollow sphere, we can moreover avoid any singularity, other than the central Big-Bang type singularity, in the astrophysics of real objects. Thus, it seems that we can eliminate several serious problems in the current astrophysics with the help of the Ni’s solution of EFEs.
Acknowledgements
The work was supported, in part, by the VEGA―the Slovak Grant Agency for Science, grant No. 2/0031/14, and by the Slovak Research and Development Agency under the contract No. APVV-0158-11.
Cite this paper
LubošNeslušan, (2015) The Ni’s Solution for Neutron Star and Outward Oriented Gravitational Attraction in Its Interior. Journal of Modern Physics,06,2164-2183. doi: 10.4236/jmp.2015.615220
References
- 1. Oppenheimer, J.R. and Volkoff, G.M. (1939) Physical Review, 55, 374-381.
http://dx.doi.org/10.1103/PhysRev.55.374 - 2. Oppenheimer, J.R. and Snyder, H. (1939) Physical Review, 56, 455-459.
http://dx.doi.org/10.1103/PhysRev.56.455 - 3. Ni, J. (2011) Science China: Physics, Mechanics, and Astronomy, 54, 1304-1308.
http://dx.doi.org/10.1007/s11433-011-4350-9 - 4. Tolman, R.C. (1939) Physical Review, 55, 364-373.
http://dx.doi.org/10.1103/PhysRev.55.364 - 5. Chandrasekhar, S. (1935) Monthly Notices of the Royal Astronomical Society, 95, 207-255.
http://dx.doi.org/10.1093/mnras/95.3.207 - 6. Landau, L. (1932) Physikalische zeitschrift der Sowjetunion, 1, 285.
- 7. Einstein, A. (1915) Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, 844-846.
- 8. Einstein, A. (1916) Annalen der Physik, 354, 769-822.
http://dx.doi.org/10.1002/andp.19163540702 - 9. Eddington, A.S. (1922) Relativitätstheorie in Mathematisher Behandlung. Alexander Ostrowski and Harry Schmidt, Göttingen and Cöthen. (In German)
- 10. Birkhoff, G.D. and Langer, R.E. (1923) Relativity and Modern Physik. Harvard University Press, Cambridge, Mass.
- 11. Schwarzschild, K. (1916) Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Classe, 1, 189-196.
- 12. Misner, C.W., Thorne, K.S., and Wheeler, J.A. (1997) Gravitation. 20th Printing, W. H. Freeman et Comp., New York.
- 13. Tolman, R.C. (1969) Relativity, Thermodynamics, and Cosmology. Clarendon Press, Oxford.
- 14. de Broglie, L. (1925) Annales de Physique, 3, 22.
- 15. de Broglie, L. (1925) Comptes Rendus de l’Académie des Sciences, 180, 498.
- 16. Penrose, R. (1969) Nuovo Cimento, 1, 252-276.
- 17. Rhoades, C.E. and Ruffini, R. (1972) Physical Review Letters, 32, 324-327.
http://dx.doi.org/10.1103/PhysRevLett.32.324






