Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60302,5 pages
10.4236/jmp.2015.613179
Ferromagnetic Calculation of Terbium Dysprosium and Holmium with Polyhedron Electron Shell
Zilong Kong
Wufangfa Computer Technology Service Department, Guangzhou, China
Email: kongzl@oceanmining.org
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 September 2015; accepted 12 October 2015; published 15 October 2015
ABSTRACT
Based on the regular polyhedron model of multi-electronic atom combined with the Bohr hypothesis, the following supposition is put forward: the electron momentum multiplied by the inscribed sphere radius of edges of each regular polyhedron is equal to the Planck constant. The relationship between saturation magnetization rates and Planck constants is determined, and the ferromagnetism of atoms is obtained from regular dodecahedron and regular hexahedron. Then, terbium, dysprosium, and holmium saturation magnetization rate are obtained from electronic regular polyhedron configuration. Derivation of matter wave formula is from thermodynamics, avoiding over speed of light.
Keywords:
Atomic Structure, Regular Polyhedron Electron Shell, Ferromagnetism of Terbium Dysprosium and Holmium, Matter Wave Formula

1. Introduction
Niels Bohr presented three assumptions in 1913: steady state assumption, quantized track hypothesis, and Bohr frequency condition [1] -[3] . Thus, the model of the hydrogen atom was established, and hydrogen spectrum was explained. The literature [4] presented and established the regular polyhedron model of multi-electronic atom, and the magnetism of iron, cobalt and nickel was explained with regular dodecahedron. This article combines quantized track hypothesis and regular polyhedron model, presents an assumption, and explains the ferro- magnetism of terbium, dysprosium, and holmium.
2. Electronic Angular Momentum on Edge of Regular Polyhedron
Page 7 of literature [4] presents the velocity of electron  on regular dodecahedron shell of iron atom, c is velocity of light. The atom radius of iron, namely, the circumscribed sphere radius of regular dodecahedron, is
on regular dodecahedron shell of iron atom, c is velocity of light. The atom radius of iron, namely, the circumscribed sphere radius of regular dodecahedron, is .
. 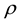 is the radius of inscribed sphere of edge,
is the radius of inscribed sphere of edge, 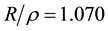 , and
, and 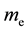 is electron mass. After the calculation,
is electron mass. After the calculation, 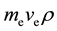 , which is equal to Planck constant
, which is equal to Planck constant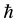 . is similar to Bohr postulates. This con- clusion can be extended to all regular polyhedron electron shells by regular dodecahedron. Thus, the following assumption is presented:
. is similar to Bohr postulates. This con- clusion can be extended to all regular polyhedron electron shells by regular dodecahedron. Thus, the following assumption is presented:
 (1)
(1)
In this study,  is the inscribed sphere radius of edge of various regular polyhedron.
is the inscribed sphere radius of edge of various regular polyhedron.
3. Magnetic Moment of Regular Dodecahedron
Formula (13) on page 6 of literature [4] demonstrates that in terms of regular dodecahedron, 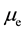 is the magnetic moment of each electron, and
is the magnetic moment of each electron, and 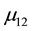 is the magnetic moment of each electron shell:
is the magnetic moment of each electron shell:
 (2)
(2)
Formula (2) on page 3 of literature [4] demonstrates that 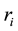 is the radius of the circular electric current, which is the radius of electron circular motion, e is quantity of electric charge:
is the radius of the circular electric current, which is the radius of electron circular motion, e is quantity of electric charge:
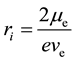 (3)
(3)
For regular dodecahedron, a is the edge length of regular dodecahedron, which is the side length of regular pentagon:
 (4)
(4)
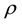 is the inscribed sphere radius of edge of regular dodecahedron:
is the inscribed sphere radius of edge of regular dodecahedron:

By using Formula (1) to Formula (5) in this paper, the following is obtained:


4. Magnetic Moment of Regular Hexahedron
For regular hexahedron, a is the edge length of regular hexahedron, which is the side length of square:



For regular hexahedron (see Figure 1), only A and B two face contribute to magnetic moment, 

By using Formulas (1), (3), (7), (8), and (9), the following is obtained:
Figure 1. Motion of electron on regular hexahedron, electrons in both A and B two face directions are same.


5. Saturation Magnetization Rate of Terbium, Dysprosium, and Holmium
The following is presented from Formula (6):

Table 19.5/1 from literature [5] provides the experimental values of the saturation magnetization rate of ferromagnetic elements, in which, the effective magneton number 
where 




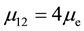
Page 18 of literature [4] indicates that the electronic configuration of dysprosium is 2, 8, 12, 6, 12, 6, 12, 6, 2, whereas holmium is 2, 8, 12, 6, 12, 6, 12, 6, 3. Regular dodecahedron and regular hexahedron contribute to ferromagnetic. Three regular dodecahedrons and three regular hexahedrons exist, and the magnetic moment of each atom is

According to Section 26.3 of literature [5] , Bohr magneton can be expressed as follows:

By using Formula (11) to Formula (14), the theoretical value of 

The electronic configuration of terbium is 2, 8, 12, 6, 12, 6, 12, 4, 3. Three regular dodecahedrons and two regular hexahedrons exist, and the magnetic moment of each atom is

By using Formulas (11) to (14) and Formula (16), the theoretical value of 

In addition, the electron shell of iron only has one regular dodecahedron. By using Formula (12) and Formula (14), the theoretical value of 

The comparison of the value of each theory value and the above experimental value indicates that the difference is small. If the paramagnetic or diamagnetic effect of other electron shell is considered, error will be smaller.
6. Derived Matter Wave Formula from Thermodynamics
In Bohr Theory, the quantum number of each electron shell is increasing, 


From the formula of thermodynamics, 

See page 10 of literature [4] , the magneton do the work is



From the above two formula, get

For multi shell of electrons, s is the number of shell, the energy 

Electronic is a wave, also 


Resonance condition

When the number of electron shell is equal to the number of the main quantum number, 

The numerical range of degrees of freedom:

7. Conclusion
In the regular polyhedron, the inscribed circle of regular polygon of edges is the electronic orbit. The radius of inscribed sphere of edges is the distance of edges to the center and is the electrons to the nucleus distances but not electronic circular motion radius. By assuming that the electron momentum multiplied by the inscribed sphere radius of edges of each regular polyhedron is equal to the Planck constant, the relationship between the saturation magnetization rates and Planck constants is obtained. The ferromagnetism of atoms is from regular dodecahedron and regular hexahedron. Then, according to the electronic regular polyhedron configuration, ter- bium, dysprosium, and holmium saturation magnetization rate are obtained. Matter wave formula can be derived from the thermodynamics.
Cite this paper
ZilongKong, (2015) Ferromagnetic Calculation of Terbium Dysprosium and Holmium with Polyhedron Electron Shell. Journal of Modern Physics,06,1776-1780. doi: 10.4236/jmp.2015.613179
References
- 1. Bohr, N. (1913) Philosophical Magazine, 26, 1-25.
http://dx.doi.org/10.1080/14786441308634955 - 2. Bohr, N. (1913) Philosophical Magazine, 26, 476-502.
http://dx.doi.org/10.1080/14786441308634993 - 3. Bohr, N. (1913) Philosophical Magazine, 26, 857-875.
http://dx.doi.org/10.1080/14786441308635031 - 4. Kong, Z.L. (2013) Journal of Modern Physics, 4, 1-19.
http://dx.doi.org/10.4236/jmp.2013.410A1001 - 5. Stöcker, H. (1996) Taschenbuch der Physik, 2. Auflage. Verlag Harri, Deutsch, Frankfurt am Main.
- 6. de Broglie, L. (1924) Recherches sur la t théorie des quanta (Researches on the Quantum Theory). Thesis (Paris).
- 7. de Broglie, L. (1925) Annales De Physique (Paris), 3, 22.



