Received 31 August 2015; accepted 2 January 2016; published 6 January 2016

ABSTRACT

It is largely believed (or strongly assumed) that photons are massless particles and the most compelling evidence there―it is said―is found in the manifestations of photons being long ranged and long lived particles. As we have done before, albeit, with a much better and clear insight in the present than before; we argue herein that massive photons can still enjoy the special and rare privilege of travelling at the speed of light c while being long ranged, long lived and most of all, obey- ing the much desired gauge symmetry. This we achieve by breaking the traditional Lorenz gauge and in its place, we introduce a new Special Gauge Condition (SGC) that does the work of assuring the photon its longevity, long range-ness and that it [photon] propagates at the speed c. However, the most melancholic outcome of our investigation is that if the present scheme is what subtle Nature has chosen to endow the photon a non-zero mass so that it [photon] still obeys gauge invariance, is long ranged, long lived and travels at the sacred speed c; then, this non-zero photon mass may be very difficult, if not impossible to measure. We use the equations developed to investigate Lorentz violation in g-ray bursts.

Keywords:

Lorentz Violation, Lorenz Gauge: Violation, Stueckelberg: Field, Mechanism-Proca: Massive Photon, Long Range Photon, Long Lived Photon

“My religion consists of a humble admiration of the illimitable superior spirit who reveals himself in the slight details we are able to perceive with our frail and feeble mind.”

--Albert Einstein (1879-1955)

1. Introduction

Despite the inconclusive experimental evidence (see e.g., Refs. [1] - [10] ), photons are largely believed to be massless and the most compelling of all evidence there―it is said―is found in their physical and natural manifestation as long ranged and long lived particles (e.g., Refs. [11] - [13] ). As we have done before (in Ref. [14] ), albeit, with much better insight in the present than before [14] ; we argue herein that massive photons can still travel at the usual speed of light, 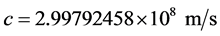, while being long ranged, long lived and in complete observance of the much desired gauge symmetry. That is to say, as occurs in the Natural World, photons strongly appear to be stable (i.e. long lived) and long ranged; a short ranged photon can not travel the vast expanse of the Universe for it will be limited in range and additionally, it will have to decay (i.e. transform into a new particle or particles) because it is short lived (cf. Refs. [15] [16] ). In accordance with prevalent wisdom (cf., Ref. [2] ), the only explanation there is as to why photons should be able to travel the vast expanse of the Universe from as way back as thirteen billion years ago and at the speed c is if and only if they are massless. This view is questioned herein.

In our earlier works (presented in Refs. [14] [17] ), we have argued that in principle, it should be possible to have massive photons travelling at the speed c while at the same time these photons are long ranged, long lived and in complete observance of the gauge symmetry. In the present reading, we present this same line of reasoning, albeit, with much better and convincing insight into the matter. In the aforementioned earlier works [14] [17] , we made use of the idea that one can in principle, as revealed in the proposed Unified Field Theory [17] , treat physical observables as 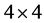matrices and with this idea, we selected (in Ref. [18] ) matrices that allow us to achieve our desired objective. However, as we continued to excogitate and ponder on these matters, it became manifest to us that one can actually use the elegant, beautiful, brilliant, neat and more convincing Stueckelberg [19] - [21] mechanism to achieve the same goal without the need for the rather strange and draconian use of matrices―which we must confess: “we where uncomfortable to use, but merely accepted them [observables as 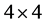matrices] as a means to a much desired end”.

Apart from the aforesaid introduction of the Stueckelberg [19] - [21] mechanism, as is the case in our earlier works [14] [17] , we herein achieve long range, long lived, gauge invariant massive photons that travel at the speed of light by breaking the traditional Lorenz [22] gauge and replacing this with a new special gauge condition. In order to make our ideas as translucent as we possibly can and as well for latter instructive purposes, we shall give an exposition of Maxwellian Electrodymanics, Maxwell-Stueckelberg Electrodymanics, Maxwell- Proca Electrodymanics and finally Maxwell-Proca-Stueckelberg Electrodymanics. Thereafter, we present our novel contribution. After making clear our contribution, we discuss the issue of Gamma Ray Bursts (GRBs) in connection with massive photons. This discussion on GRBs is not the prime focus of the present reading but an offspring of it, albeit, an offspring that requires serious attention in future readings. That is, the present reading merely sets the foundations for these future readings and nothing more. Lastly, we give a general discussion and the conclusion drawn thereof.

2. Maxwellian Electrodymanics

In its classical form, Maxwellian Electrodynamics (MED) is described by two pristine and condensed tensor equations-namely, the source coupled and source free field equations. The source free field equations are given by the equation:

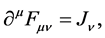(1)

where:

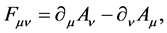(2)

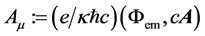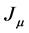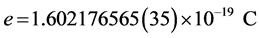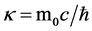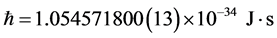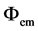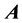is the MED field tensor, is the four MED vector potential and is the four current: is the electronic charge, is mass term that we here have inserted for convince, is Planck’s normalised constant, and are the electrical

potential and the magnetic vector potential respectively. In the present reading, the electromagnetic four vector potential is a dimensionless quantity. The four current 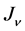has dimensions of per unit square of length and in-terms of electrical charge density (with SI Units) and current (with SI Units), we shall write, where, is the permit- tivity of free space.

The source free field equations are given by the equation:

(3)

where is the Levi-Civita tensor. Of particular interest in the present reading is the source coupled Equation (1), and not not (3) and as such, we shall not-after the present section-come back to this Equation (3). From these two tensor Equations (1) and (3), we can write down the four Maxwell’s equations which we are used to, and, much readily identify with, i.e.:

(4)

(5)

(6)

(7)

where, is the permeability of of free space; and B are the electric and magnetic fields respectively, and, is the electric charge density.

Now, substituting (2) into (1), we will have:

(8)

where is the usual D'Alembert operator. Introducing the Lorenz [22] gauge condition i.e.:

(9)

it follows that Equation (8) will reduce to:

(10)

Given the Lorenz gauge (9) and using the following definitions and, one can write from (3) and (10) the usual four standard Maxwell’s Equations (4, 5, 6 & 7) of electromag- netism.

By applying the methods of least action, the source coupled Equation (1) is derived from the Maxwellian Electrodynamic Lagrangian:

(11)

by submitting this Lagrangian (11) into the Lagrangian equation of motion, namely:

(12)

The Lagrangian (11) is invariant under the following gauge transformation:

(13)

where is a dimensionless, arbitrary well behaved smooth function (i.e. differentiable, integrable and uniform continuous function), is a constant with the dimension of inverse length and this constant has been inserted for dimensional consistency (remember we have chosen to be a dimensionless quantity).

Now, it may not be immediately clear that the Lagrangian (11) is invariant under the gauge transformation (13) because this transformation leads to this Lagrangian (11) now becoming:

(14)

As is well known, the MED tensor field is obviously invariant under the gauge transformation (13); the issue which-at a prima facie level of analysis may make the Lagrangian (11) appear to be not invariant under the gauge transformation (13) is the new term appearing in (14). However, this term can be “whisked” away by showing it to be equal to zero.

For example, Srednicki [23] has argued that because is conserved quantity (i.e.,), the term can be written as i.e.. With now written as, it is now the divergence of the four vector. As Srednicki [23] argued, one can always find suitable boundary conditions that will always make, so that this “gauge-spoiling” and “nagging” extra-term appear-

ing in (14) vanishes identically. In this way, the Lagrangian (11) is clearly invariant under the gauge transforma- tion (13). So far, so good, let us proceed to Maxwell-Stückelberg Electrodymanics and let us call the photon(s) described by MED as presented here-MED photon(s).

3. Maxwell-Stückelberg Electrodymanics

Another way to make the Lagrangian (11) invariant under the gauge transformation (13) without having to relay on a judicious process and selection of boundary conditions is to add a Stückelberg scalar field to the Lagrangian (11) so that they obtain a new modified MED Lagrangian which is best called the Maxwell- Stückelberg Electrodynamic (MSED) Lagrangian; this Lagrangian is such that:

(15)

The Stückelberg scalar field shall be assumed to be dimensionless quantity-the reader needs to keep this in mind. The addition of such a scalar field into the equations of electrodynamics was conducted for the first time in 1938 (see Refs. [19] - [21] ) by the brilliant but less known Swiss mathematician and physicist-Ernst Carl Gerlach Stückelberg (1905-1984).

This MSED Lagrangian (15) is invariant under the following pair of gauge transformations [24] :

(16)

To obtain the MSED field equations from this Lagrangian (15), via the method of least action, we substitute this MSED Lagrangian into the following Lagrangian equation of motion:

(17)

from which one obtains the usual massless photon MED field Equation (1) and the Stückelberg scalar field disappears completely from the midst of the resulting field equations. Its job [Stückelberg scalar field] here is the restoration of the much desired gauge symmetry. In the Standard Model, it can also be used to get ride of the Higgs boson [25] - [27] in just about the same manner. Again, so far so good, lets proceed to present an exposi- tion of Maxwell-Proca Electrodymanics and let us call the photon(s) described by MSED as presented here- MSED photon(s).

4. Maxwell-Proca Electrodymanics

As is well known, Maxwellian Electrodynamics (MED) is based on the hypothesis of a massless photon. If at all, what evidence there is to this, experience is yet to furnish us with a solid answer. As regards the quintessence of a zero-mass photon is the resulting gauge invariance of MED i.e., to those that seek beauty in a physical theory, one appealing feature of MED is that it quantum mechanical version i.e. Quantum Electrodynamics (QED) is constructed from a gauge invariant Lagrangian which does not need either the Stückelberg scalar field nor the special boundary conditions to attain gauge invariance. From an Ockham Razor’s stand-point the QED would be the most preferred Lagrangian.

Gauge invariance was first introduced by the great German mathematician, mathematical physicist and philosopher-Professor Herman Klaus Hugo Weyl (1885-1955) [28] - [32] ; it plays a central role not only in field theory but in physics as a whole-it is a principle without which, modern field theories could not be. However, if one abandons this (gauge symmetry), they can as the great Romanian physicist Professor Alexandru Proca (1897-1955) did (in the works [33] - [41] ); construct an electrodynamic theory were the photon has a non-zero mass via the Proca Lagrangian, that is:

(18)

The resulting source coupled Maxwell-Proca field equations are:

(19)

This Equation (19) is the classical Maxwellian Electrodynamic field equation with it added the Proca mass term,.

In one of the early Solar system investigations of Maxwell-Proca electrodynamics, the great Austrian physicist-Erwin Rudolf Josef Alexander Schrödinger (1887-1961) was perhaps the first [42] [43] to write down the source coupled Maxwell-Proca equations in the form they are written in (20) and (21), namely:

(20)

and:

(21)

In seeking a photon mass, both laboratory and astronomical observations focus on the two extra terms and. As shall be seen in the proposal that we make herein, in the case of, the special gauge condition that we are going to introduce is going to whip away these two terms (and) leaving the

usual Maxwell’s source coupled equations with a vanishing mass term. What this means is that if once tried to use MPED to decipher a non-zero mass for the photon, they will not detect a non-zero mass but a vanishing mass because it has been `whipped' away despite it being non-zero. Therefore, the special gauge condition that we shall introduce renders it difficult if not impossible to detect a non-vanishing photon mass-this put the question of a non-zero mass into a serious anti-juxtaposition because, in the end, laboratory and astronomical observations that employ MPED to detect a non-vanishing photon mass via the terms and, these are here made inadequate to discern if the photon truly has a vanishing mass. In-closing, let us call the photon(s) described by MPED as presented here-MPED photon(s).

5. Modified Maxwell-Proca-Stückelberg Electrodymanics

Contrary to physical and natural reality, Proca’s massive photon theory leads to short-lived and short ranged photons and this is one of its greatest setbacks insofar as Electrodynamics of massive photons is concerned. Short-lived and short ranged photons would do well for the Standard Model, but not for the seemingly long- lived and longed ranged electromagnetic interaction. Additionally, the resulting Lagrangian of massive photons is not readily gauge invariant. In a very simple and trivial manner-as did Stueckelberg [19] - [21] , we will modify the Maxwell-Proca Lagrangian by introducing a Stückelberg scalar field and in addition, we shall introduce

a special gauge condition. The modified MPED Lagrangian, which we shall call the Maxwell-Proca-Stückelberg (MPSED) Lagrangian is given by:

(22)

This Lagrangian is the same MPED Lagrangian albeit with the four electrodynamic now replaced with. Just as the MPED Lagrangian (15) is invariant under the gauge transformations (16), this

Lagrangian (22) is also invariant under the same gauge transformations. So, the issue of gauge invariance is no issue at all. The real issue is that the resulting MPED equations requires that photons must be short-lived and short ranged because the mass-term exists in the resulting equations. We will see this in the subsequent subsection.

Special Gauge Condition

To obtain the resulting field equations from the Lagrangian, we have to substitute this Lagrangian into the the Lagrangian equation of motion (17) (i.e.,) and then apply the methods of least action, in which event one will obtain the following field equations:

(23)

Because of the existence of the mass-term, this Equation (23) leads to short ranged and short lived (massive) photons-something that is at odds with physical and natural reality as we currently understand. The good news is that this can be overcome by introduction a special gauge condition. To see this, we shall first unpack the field tensor so that this Equation (23) is now written equivalently as:

(24)

The Special Gauge Condition (SGC) that we shall introduce so as to attain the desired theory of massive photons that are gauge invariant, long ranged and long lived is to set the terms in the under-brace [in (24)] so that these terms are identically equal to zero, i.e.:

(25)

The resulting equation after the introduction of the SGC, is:

(26)

and this equation is the same as Equation (10) for a massless photons in MED theory. At this point we are done with what we intend to achieve insofar as long range, long lived and gauge invariant massive photons are concerned. However, if we are to leave it at this point, a lot of questions about the Stückelberg scalar field will remain unanswered. To avoid clamping too many issues in one reading, we shall try and answer these questions but not with the level depth that is required because this would require a separate reading (or maybe readings) altogether, therefore, the reader with a strong taste for thoroughness must surely forgive us in this instance. In-closing, let us call the photon(s) described by MPSED under the proposed SGC (25) as presented here-MPSED photon(s).

6. Stückelberg Scalar Field

We have shown that massive photons can exist without the three major problems that are normally associated with massive photons, that is, the problems of them being short ranged, short lived and non-gauge invariant. This achievement has come at a severe cost, namely that the Lorenz gauge is to be done away with. We now move one step further by resetting this gauge so that it is now given by:

(27)

where is dimensionless constant-this constant is a fundamental and universal constant just as is the Planck constant, Newton’s universal constant of gravitation G etc. If this constant is equal to zero,

then we are back to the usual Lorenz gauge [22] and this leads us to the normal MPSED theory. With (27) as given (i.e.,), it follows that taking the four divergence of the new gauge condition (25), one will have:

(28)

and given (27), it follows that the resulting equation is an equation for the field and this equation is:

(29)

which is the Klein-Gordon equation for the Stückelburg scalar. If, then, the Stückelburg scalar is a tachyon-the meaning of which is that it moves at the a speed greater than the speed of light; and if,

then, despite it having a non-zero mass, the Stückelburg scalar will either move at a speed less than, or, equal to the speed of light. We need to explain the latter-for the present purposes, we will ignore the tachyon solution.

If, it is expected from Einstein's Special Theory of Relativity (STR) [44] that this massive Stückelburg scalar will propagate only at a speed less than the speed of light. The STR will certainly have

problems with such a particle propagating at the speed of light since it is massive-for massive particles, are, according to the STR incarcerated to travel only at speeds less than the speed of light. Against this background, we have argued in an earlier reading [14] that if the mass is a function of the wavelength (or wave-number k) i.e., it should in principle be possible for a massive particles to propagate at the speed of light c.

Now, since the massive Stückelburg scalar is coupled to the photon, it must propagate at the same speed with the photon-it must propagate at the speed c. This is the assumption that we shall adopt, the meaning of which is that we shall assume for the Stückelburg scalar that.

The Stückelburg scalar is not-in general-expected to have the same energy and momentum as the photon, its energy and momentum can be different and we shall take this assumption that the photon and Stückelburg scalar

have different energies and momentum. In general, the wavefunction of a free Stückelburg scalar is, where N is a dimensionless normalization constant and where and are the momen- tum and energy of the Stückelburg scalar. Substituting into (29), one will obtain the energy- momentum equation for the Stückelburg scalar which is:

(30)

where. For the purposes of this reading, we shall assume. Further, we shall assume that the energy and momentum of the Stückelburg scalar is extremely tiny, so tiny that is nearly equal (but not equal) to zero i.e. and respectively. This naturally means that. As will be seen in the next section, if the quantities are significantly large, there would exist significantly large cosmological electric fields.

7. Orbital Angular Momentum of the Stückelberg Scalar

It turns out that the rate of change of orbital angular momentum of the Stückelberg scalar can be fixed and this fixture is so as to conform with observations. To do this, we have to re-look at the way the electrical field is defined. The magnetic field will remain defined as but the electric field takes a new definition in the face of the new Lorenz gauge (27), it (electric field) will have to be defined as:

(31)

where a new electrical field, , enters the fold, this electrical field we shall call the Stückelberg Electrical Field (SEF) because it is as a direct result of the Stückelberg scalar field. To see how this comes about, we have

to take the -component of (26), i.e.. We know that:

(32)

and this can be rewritten as:

(33)

From the new Lorenz gauge (27), we have:

(34)

and given that:

(35)

where, together with its integral-this functions is defined at, then, the second term on the right hand-side of the above equation, can be rewritten so that we have:

(36)

and further:

(37)

hence:

(38)

and from this, we obtain the first of Maxwell's field Equation (4), namely,. This is how the new definition of comes about.

Notice that the Stückelberg field will exist even for an electrically neutral particle with a static magnetic vector potential i.e.. In MED, these condition will lead to. What this means is that

this field must be present in all matter, including the electrical neutral neutrino. Because no significant electrical field has been measured around a neutrino, this field must be extremely small. It must be so small that it is only significant on cosmic scales. If this field exists in all matter, then, the Universe must be filled with a tiny all- pervading and permeating cosmic electrical field.

Now, given that, it follows that Equation (31) will reduce to:

(39)

Further, taking the curl of, it follows from (39) that we will have:

(40)

Evaluating-in rectangular Cartesian coordinates-the expression, we will have:

(41)

From (41), it is clear that in-order for us to obtain the complete set of the usual equations that we are used to know, i.e., Maxwell’s Equations (4, 5, 6 & 7), the Stückelberg scalar field will have to have a non-changing orbital angular momentum i.e.; therefore, once set, its orbital angular momentum never changes-it is fixed from antiquity to eternity.

Clearly, if, this would lead to a testable prediction of the existence of the Stückelberg scalar field because the new extra-term would constitute the much sought for and desired measurable prediction. To keep matters as simple as possible at this stage, we will assume. This keeps us well within the confines of our present boundaries of knowledge.

8. Time Delays in Gamma Ray Bursts Events

One of our real motives [14] in the investigation of the possibility of massive photons has been to make an endeavour at an answer to the problem of time delays observed in Gamma-Ray Burst (GRB) events where it has been observed that g-rays of different energies emanating from the same event arrive at the telescope at different times. These g-rays are supposed to propagate at the speed of light c. GRBs where accidentally discovered and first reported in 1973 by Klebesadel et al. [45] and these GRBs seem to hold potent seeds to probe Lorentz invariance via the observed time delays in the arrival times of g-rays of different energies from these GRBs events. Lorentz invariance is a very important fundamental symmetry in physics and its violation-if confirmed by experiments; can have serious reverberations across all disciplines of physics.

8.1. Lorentz Invariance

As is well known, a cornerstone of Einstein’s STR [44] is Lorentz invariance, i.e., the postulate that all observers in the Universe measure exactly the same speed of light c, in vacuum, independent of the photon’s energy. The different arrival times of photons of different energies emanating from the same GRB event suggests (amongst other possibilities) a violation of this seemingly sacrosanct Lorentz invariance predicted by the STR.

A great effort is currently under-way to investigate possibilities of Lorentz violations [46] - [51] on both the quantum and macro-scale. These violations are being sought in laboratory experiments [10] [52] , in the Solar system, on the galactic [53] [54] and cosmological scales. At present, one can safely that, more than in any field of scientific endeavour, Lorentz violations are a major derive for those seeking to tie together Einstein’s General Theory of Relativity (GTR) and Quantum Theory (QT) into a Quantum Gravity (QG) theory. The majority of

these quantum gravity efforts seek to find deviations in the Einstein energy-momentum relation. Any deviations, will even in the case, lead to an energy dependant speed of the photon.

One such deviation that has been proposed and continues to enjoy a great deal of attention is the proposal by the Italian physicist-Professor Amelino-Camelia et al. [55] - [58] , namely:

(42)

where are free parameters to be determined by experiment and is the invariant energy scale where quantum gravity effects are expected to dominate. The QG energy scale, , is expected to coincide with the Planck energy scale, i.e.: where, here, the constant, , is Newton’s universal constant of gravitation. Assuming that is a constant quantity, then, Equation (42) leads to an energy dependent speed of light [55] - [58] .

Against this background, if the outcome of the present investigations are to accepted, then, it is no longer tenable (for us-at least) to ascribe this time delay in the arrival times of these g-rays of different energies to the mass of the photon as the present ideas are translucently clear in that massive photons will-in a vacuum, travel at the speed of light, c. That is to say, in a vacuum, the present ideas predict that, and, which is just the same as in MED theory. Apart from resorting to exotic ideas such as those being championed in attempts of QG, our only hope-if we are to explain these time delays as being caused by wavelength dependence of the speed of light, is to drop the assumption that the intergalactic space may not be a perfect vacuum as we suppose, i.e., the great expanse of cosmic space is not the supposed perfect vacuum that allows photons to propa- gate at the speed c, it [cosmic space] may very well be a conductive medium allowing photons to propagate not at the speed c. We shall make a pedestrian exploration of this idea in the subsequent subsection.

8.2. Conductive Cosmological Medium

Photons will propagate at the speed c only in a perfect vacuum where the refractive index (n) is unity. On that note, it is worthy asking if the Intergalactic Medium (IGM) is a perfect vacuum. Are the intestacies of the spaces between galaxies truly empty to constitute a perfect vacuum? A frank and honest answer to this important question would be-“No, the IGM is certainly not a perfect vacuum and there are a number of reasons for this. Stars, pulsars, the Active Galactic Nuclei (AGN) etc are constantly pouring out and into the IGM charged particles.” Therefore, the IGM ought to comprise (albeit tiny) electrical currents due to the moving protons, electrons and elementary particles.

Actually, the IGM is known to be a rarefied plasma [59] [60] consisting mostly of ionized hydrogen; i.e. a plasma consisting of statistically equal numbers of electrons and protons. Therefore, the refractive index of the IGM and cosmological space in general can not be identically equal to unity because of this cosmological, galactic and astronomical rarefied plasma and the interstitial magnetic fields. In a such a medium, the speed of propagation of a photon will certainly dependent on its wave-length as it does here in earth laboratories in the different mediums such as glass, water, salt solutions etc. Apart from the rarefied plasma, there exists in the IGM the Intergalactic Magnetic Fields (IGMFs) [61] [62] and as-well cosmological Primordial Magnetic Fields (PMFs) [63] [64] . Logically, it therefore makes sense to imagine or assume that the vastness of all the cosmological space of the observable Universe must be filled with a rarefied plasma. This is the assumption that we shall take.

If the SEF is all around and filling the cosmological space as hypothesised, then, the rarefied cosmological plasma must have non-random electrical currents but electrical potential driven currents. If-as is the case in Earth based laboratories-these electrical currents obey Ohm’s Law where is the conductance of this cosmic plasma, then, the wave equations for and which in a perfect vacuum (where) are given by and, these equations will now be modified and will become:

(43)

(44)

Assuming for and the wavefunctions and where and are constant vectors and is the four wavenumber, then, these two wave Equations (43) & (44) yield the following dispersion relation:

(45)

Given that the group velocity of a wave is given by, it follows that the refractive index (n) of this medium will be given by:

(46)

Further, if, then, to first order approximation (46) will reduce to:

(47)

We can rewrite (47) as:

(48)

where is the energy of the photon under probe and is a property of the rarefied cosmic plasma; the value of is a measure of rarefied cosmic plasma's electrical conductance.

From this Formula (48), if; and we have two photons such that and and are their group velocities respectively, then,; and on the same pedestal, if; then, for the same photons, we will have. Observations indicate the latter is the case, that is:.

High-energy g-ray photons from GRB events arrive at Earth only after lower-energy g-ray photons have arrived. Accepting this reality, this means that we must have, the meaning of which is that the conductance of the cosmic plasma is a positive.

At this point, let us digress a little and ask the question “What does a positive (or negative) conductance?” To answer this question, we need to realize that in the derivation of Equations (43) and (44), we assumed Ohms Law. In Ohms Law, it is assumed that the electrical current is due to the motion of electrons, that is negative electrical charges. These (electrons) propagate in the direction of increasing electrical field. This is the reason why. If electrical currents where due to the motion of positive electrical charges, the electrical conductivity will have to be negative because positive charges will propagate in the direction of decreasing electrical field. The fact that for the cosmic plasma we have, this means that negative electrical charges dominate this cosmic plasma instead of positive electrical currents. This is more of what one would expect from logic, intuition, common sense and experience.

Now, after the above digression, let us proceed with the main business of the present section. We want to derive a formula that will allow us to compute the time lag per unity energy difference. For this, we need first to compute. From (48), it follows that:

(49)

Let D be the actual physical distance from Earth where with GRB has occurred and let t be the time taken for this flush to travel from the moment of emission to when it is observed on Earth. We know that, from

which it follows that. If is the measure of the change of the speed of light from its vacuum speed c, then, the meaning of which is that:

(50)

so that:

(51)

The distance D is the light-travel distance or the look-back time. Assuming a Friedman Universe-

i.e., the expanding Universe within the framework of the standard Cosmological-Constant Cold-Dark-Matter (LCDM)-model; and that the redshift is solemnly due to the expansion of the Universe, then, this distance D is given by:

(52)

where and are the matter-density and the darkenergy-density parameters as currently measured, respectively; [65] is present day Hubble parameter.

The result (51) is an exact result which can be put to the test if all the parameters are known. What is required are four parameters, namely the time lag, the two energies of the photons and the distance D to the GRB. Of these four parameters, the distance D is most uncertain and in-doubt. This distance is usually measured by inferring it from the redshift of the GRB. These GRB redshifts typically exceed unity (i.e.,) and assumed to be Hubble redshift. The assumption that these redshifts are Hubble redshifts (i.e., cosmological in nature) means that these redshits are solemnly due to the expansion of the Universe and nothing else, there exists no extra-redshift component such as perhaps the gravitational redshift etc. To illustrate our uneasiness at interpreting these high redshifts as been purely cosmological in nature, we shall briefly talk about the so-called Quasar Redshit Controversy (QRC).

The majority of known quasars have very high redshifts, sometimes as high as. The so- called QRC, is the issue of whether or not these redshift of Quasars are of a cosmological nature (cf., Refs. [66] - [70] ), that is, are they solemnly due to the expansion of the Universe or there exists other additional non- cosmological mechanisms giving rise to a significant portion of these redshifts? In the May 1967 issue of the Astrophysical Journal, Prof. Halton Christian Arp (1927-2013) identified a number of instances in which the data available from observations indicated-in his vested opinion-that pairs of objects-radio galaxies or quasars had been ejected in opposite directions as a result of explosive events taking place in large central galaxies [71] . Prof. Arp went on the identify a number of Quasar-Galaxies association [72] [73] . If Prof. Arp’s hypothesis is correct, it would mean that quasars are not at the cosmological distances i.e., at distance that correspond to their full redshifts, but are at ordinary galactic distances. Prof. Arp’s hypothesis has received support from a significant number of astrophysicists (see e.g., Refs. [67] [74] ), but the majority of his colleagues in the astronomical profession have preferred that quasars be at their cosmological distances [66] and this is so largely because any departure from the standard redshift distance relation raises a very awkward question as to the nature and origin of the excess redshift and possible a need to rethink the the current Standard Cosmology Model-the so-called Big Bang Model.

Because of the above said, it is our strong opinion that there is need for one to seriously consider the issue of how to interpret high redshifts because distances are very important in astronomy and cosmology. If we get them wrong, all our beautiful results that we currently obtaining are like castles built in the air high above the clouds, for soon and very soon, when truth finally catches up with us, our castles will not be spared by the ever present “gravitational force”, these beautiful castles will just crash on touching the ground. We must say; we are only comfortable working with low redshifts. With these low redshifts, the error in the distance estimation is obviously much smaller than in the case of very large redshifts. The high redshifts of GRBs may just suffer the same fate as quasar redshifts. There is need to verify beyond most doubt whether or not high redshift objects-in this case high redshift GRB; are at their cosmological distances.

Therefore, in the crude calculation that we are going to make below, we shall consider two low redshift GRBs. In this case of low redshifts GRBs, we know that to first order approximation D is such that (this is the Hubble distance). This means that for such GRBs-for the quantity, we will have:

(53)

Now, by considering two low redshift GRBs, we shall use Equation (53) to compute a “rough” estimate of the conductance of the cosmic plasma. From the data of the GRB PKS 2155-304 [75] - [77] , where, , , , , one obtains, and; from the data of the GRB Mrk501 [78] [79] , where, , , , , one obtains. From these two values i.e., one obtains that. Metals have conductances

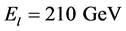
whose magnitude is of the order (e.g., [80] - [82] ). Clearly, from this rather quick “back-of-the- envelope” calculation, we see that the rarefied cosmic plasma (if it really exists, it) is a poor conductor of electricity, its conductance is about seven times orders of magnitude smaller than that of ordinary metals.

If the idea that we have just proposed of an all-pervading and permeating rarefied cosmic plasma and the SEF is acceptable, and the time delays of g-rays of different energies are to be measured accurately for most if not all the GRBs, then, a sky-map of the conductance of this plasma can-in-principle, be made. A test of the correctness of this idea would be if the same value of is measured along the same line of sight independent of the GRB and the energy regime under probe; this is so because, logically, one does not expect the same space to have two (or more) different values of. We hope that other researchers will take up this challenge. Surely, producing an all-sky map of must give importance to these time delays.

9. General Discussion

For good reasons largely to do with aestheticism, physicists have nursed a “phobia” against massive photons. They have laid three very strong charges against them; the first of which is that, such photons will have be short ranged-the meaning of which is that they would not be able to traverse―as they do―the vast expanse of the observable Universe; the second being that such photons should not be able to live long and last and most of all, against the desideratum of the purest soul of the theoretical physicist, such photons would sacrilegiously violate the sacrosanct and embellished symmetry of gauge invariance.

Of these three serious charges laid against them, we have demonstrated herein that massive photons (i.e., MPSED massive photons) can be acquitted―there really is no case against them. These charges come about if we assume MPED and as-well that the electromagnetic four vector potential obeys the Lorenz gauge [22] . By doing away with the Lorenz gauge [22] and introducing a special gauge condition (25), all these charges against massive photons can be dropped forthwith.

In the framework of MPED (which is our current best model for massive photons), if photons really did have a non-zero mass and they travelled from one end of the observable Universe to the other―as they do in Nature, then, the vast size of the observable Universe (given by) sets a stringent lower

limit of for the mass of the photon. Their lifetime must be much larger than the current estimate of the age of the observable Universe i.e.. Laboratory and observational measurements find upper limits (see e.g., Ref. [2] ); this is many orders of magnitude compared to the stringent cosmic limit required to account for photons that we observe coming from the very edge of the observable Universe at ~13.6 billion light years.

Insofar as the present findings are concerned regarding these measurements in all their range of diversity, novelty and ingenuity, what is deeply disturbing about the present acquittal is that, if photons really did have a non-zero mass and these photons are MPSED photons, then, this mass may be concealed from any kind of revelation by Nature to such an extent that scientific experiments may not be capable of positively detecting this non-zero mass. Anything that is not measurable surely is outside of the realm of science since science concerns itself with matters that can be put before the Grand Jury of Science via the inviolable and embellished methods of scientific experimentation and enquiry.

We can not help but express our greatest and deepest disappointment at the result that we have obtained herein. Yes the result maybe very important-and perhaps beautiful; but the very fact that it can not be put to the test is not only disturbing and ugly but repugnant to the purest soul of the searching theoretical physicist. How are we to take of it? That the issue of the mass of the photon is a metaphysical issue? How does a scientist accept this? This result is akin to that of the great Austrian mathematician, logician and philosopher-Kurt Gödel (1906-1978)’s incompleteness theory of 1931. That is, to have an idea that tells you of the shorting comings, in this case, we have this idea that is telling us that yes, the photon may or may not have a mass, but, whatever the case, it will be very difficult is not impossible to discern. Surely, how does one handle such matters in experi- mental or even abstract philosophy?

Apart from the the said three charges, physicists have held another diabolic charge against massive photons- namely, that they can not possibly travel at the speed of light c as this would lead to a serious and chronic problems with Einstein’s widely accepted STR [44] which now is taken by a majority of physicists as not just a theory but an indelible fabric and garment of the Law of Nature. This charge physicists have not actively brought it against photons, but merely pointed out that this serious charge can be levelled against massive photons should these massive photons be acquitted of the three paramount charges against them. The present acquittal not only clears massive photons of these three charges, but also of this reserve charge as it is clear from ideas presented herein that these massive photons will travel at the speed of light c in vacuum.

Another less publicised problem associated with massive MPED photons is that such photons will have three extra degrees of freedom [2] [83] because, apart from their transverse degrees, there would have an extra set of degrees of freedom from longitudinal degree of freedom that comes about due to the fact that a mass photon does have state of rest/rest frame. The total energy E of a “normal” massless photon at a temperature T is

. According to the equipartition theorem, adding three degrees of freedom will result in the photon gaining an extra amount of energy namely, leading to its total energy being.

If one where to take this into account in deriving Planck's radiation law-then, in complete contradiction with results from experimental philosophy, this would alter the Planck’s radiation law by a factor of 3/2. Such a paradigm shift would be measurable [83] , thus constitutes a clearly testable prediction of “any” massive photon theory.

On that note, i.e. existence of extra degrees of free for a massive photon, one will have to ask how these extra degrees of freedom come about? The answer is that they come about because these massive MPED photons do have a rest frame. They have a rest frame because of the very fact that-their having a non-zero mass, allows them to be brought to rest or at least to have in principle a rest frame. Normal massless MED photons have no rest frame whether in-principle or in practice, they always are travelling. The SGC (25) that we have introduced assures massive MPSED photons of this special state of not having a rest frame as they will always travel at the speed of light c in vacuum. They do not have a rest frame as is the case with massive MPED photons. Therefore, these massive MPSED photons are not longitudinal photons, they will result in the Planck's radiation law that we are always used to know.

The scheme that we have proposed herein to endow MPED photons with mass while at the sametime concealing it, this mechanism can not in-principle applied it to the Standard Model without any new modifications; it can not possibly be used in its bare form to endow the quantum gauge bosons of the Standard Model with mass, since these quantum gauge bosons of the Standard Model are short lived and short ranged because the SGC that we have introduced will-against physical and natural reality―make them long lived, long ranged.

For example, Sonoda & Tsai [25] , constructed a Higgs free (i.e., without the Higgs boson) generalized Stückelberg mechanism for the Electroweak gauge theory and his proposed mechanism preserves all the successful low energy predictions of the standard Glashow-Weinberg-Salam model albeit, with no physical scalar particle―the Higgs boson. The same is true with the Stückelberg mechanism of the present reading; it introduces no Goldstone boson which requires a mechanism to “eat-up” this Goldstone boson as happens in the popular Higgs mechanism [84] - [86] believed to be the mechanism by which fundamental and elementary particles are thought to acquire their mass. In this model of Sonoda & Tsai [25] , the SGC that we employed is not used by Sonoda & Tsai [25] . If one invokes it (in Sonoda & Tsai [25] ’s model), they will surely obtain long

ranged and long lived bosons.

In closing, allow us to say that the idea that we have presented here, i.e., the idea of massive long range, long lived and gauge invariant photons is an exact idea, while the consequences thereof are only exploratory in nature. These consequences are this idea’s implications on GRB with regard to the observed time delays in the arrival times of g-rays of different energies. There certainly is need for a detailed exploration on this matter. All we can say is that these ideas surely look promising and worthwhile for further investigations if we are to understand Nature at a much deeper level than at present.

10. Conclusions

Assuming the acceptability of the thesis presented herein, we hereby lay down the following as our inescapable conclusion.

1. As has been demonstrated herein, the misgivings physicists have of massive photons―i.e., misgivings derived from the assumption of Proca Electrodynamics and the Lorenz gauge [?], namely that against physical and natural reality as we experience it, massive photons are expected to be short ranged, short lived and in contempt of the sacrosanct symmetry of gauge invariance; these misgivings can easily be “whisked” away by (a) the introduction of a Stückelberg scalar field, (b) the dropping of the Lorenz gauge [as herein done at the instance of Equation (27)] and the subsequent introduction of a new special gauge condition [as herein conducted at the instance of Equation (25)].

2. Apart from the pleasant outcome mentioned above, the most melancholic outcome of our achievement is that if the present scheme is what Nature has chosen to endow the photon with a non-zero mass so that this massive photon obeys gauge invariance, is long ranged and long lived; then, this photon mass may be very difficult if not impossible to measure because the terms involving its mass are concealed from the dynamic equations by the SGC. There seems to be no way to detect this non-zero mass except perhaps by directly detect- ing the Stückelberg scalar field which may very well be inseparable from the massive photon field thus making it impossible to detect. Separation of the massive photon from the Stückelberg scalar field must result in the decay of the photon into a stable particle-antiparticle pair (i.e.). The fact that photons have never been observed to decay into a stable particle-antiparticle pair, is evidence that the Stückel- berg scalar field (if it exists to begin with) may very well be inseparable from the massive photon field hence impossible to detect.

3. The scheme that we have proposed herein to endow the photon with mass while in principle one can apply it to the Standard Model, albeit, with new modifications; it can not possibly be used in its bare form to endow the quantum gauge bosons of the Standard Model with mass, since these quantum gauge bosons of the Standard Model are short lived and short ranged because the SGC that we have introduced, despite the preservation of the much desired gauge symmetry, this will―against physical and natural reality―make them long lived, long ranged.

4. If Lorentz Invariance is an exact and inviolable symmetry of Nature, then, as we have suggested herein, namely that, the apparent Lorentz violation measured in GRB events, this can in principle be explained (amongst a set of possibilities) if the great expanse of cosmological space is filled with a rarefied cosmic plasma which is itself dominated by non-random currents due to negative electrical charges. These negative charge electric currents lead to; if these currents where to be positive charges, then. As happens here on Earth in our laboratories where the speed of electromagnetic radiation is dependant on the photon’s energy, the observed g-rays of different energies from these different GRBs events, will likewise, travel at different speeds due to the non-unity refractive index of the rarefied cosmic plasma leading to time lags for g-rays of different energies. In our view, this is a possibility that requires serious attention than has been conducted herein. All we have done in this regard is to make a perdurable suggestion that, this is a possible and viable explanation to the observed time lags in the arrival times of g-rays of different energies. This possibility upholds Lorentz invariance as an exact and inviolable symmetry of Nature.

Cite this paper

Golden GadzirayiNyambuya, (2016) Long Range, Long Lived and Gauge Invariant Massive Photons via Stückelberg Scalar Coupling. Journal of Modern Physics,07,7-24. doi: 10.4236/jmp.2016.71002

References