Journal of Modern Physics
Vol.06 No.11(2015), Article ID:59526,3 pages
10.4236/jmp.2015.611149
Chemical Affinity and the Density of Energy Levels
M. B. Saikhanov
Complex Research Institute, Russian Academy of Sciences, Grozny, Chechen Republic, Russia
Email: saikhanov_musa@mail.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 August 2015; accepted 8 September 2015; published 11 September 2015
ABSTRACT
It is shown that the state of chemical equilibrium of a closed system corresponds to the minimum density of its energy levels.
Keywords:
Chemical Affinity, Closed System, Chemical Equilibrium, Density of Energy Levels, Total Entropy Production, Lyapunov Function

1. Introduction
The concept of chemical affinity (A) was introduced into thermodynamics by Belgian physicist Théophile de Donder in 1922 to represent the driving force of a chemical reaction considered as the irreversible process [1] . Later, it has been found that this concept is very useful for the description of kinetic processes in surface layers, in particular, for investigations of the adsorption and chemisorption processes and the appearance and stable existence of coherent structures in chemical and biological systems [2] [3] . This is indicative of a fundamental character of the concept of chemical affinity as a new intensive thermodynamic parameter determining variation of the number of particles in the system.
The present work is an attempt to understand this important concept on the microscopic level, proceeding from the definition of entropy in quantum statistics (as proposed by Planck in 1925) and the notion of the density of energy levels of a closed system, which plays an important role in modeling the kinetics of nonequilibrium systems [4] -[6] .
2. Main Results and Discussion
The chemical affinity is defined as the algebraic sum of chemical potentials of the initial reactants and products multiplied by the corresponding stoichiometric coefficients:
 , (1)
, (1)
where 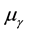 and
and 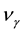 is the molar chemical potential and stoichiometric coefficient, respectively, of component
is the molar chemical potential and stoichiometric coefficient, respectively, of component 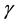 participating in a chemical reaction [1] . Taking into account that the stoichiometric coefficients of reactants are negative quantities, while those of products are positive, expression (1) can be rewritten as
participating in a chemical reaction [1] . Taking into account that the stoichiometric coefficients of reactants are negative quantities, while those of products are positive, expression (1) can be rewritten as
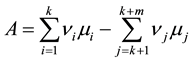 . (2)
. (2)
Here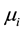 ,
, 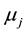 and
and ,
, 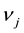 are the molar chemical potentials and stoichiometric coefficients of the reactants and the reaction products, respectively. In the state of equilibrium, the chemical affinity is zero; for a reaction proceeding in the forward direction (in excess of reactants), this value is positive, while the reverse reaction (in excess of products) has a negative affinity.
are the molar chemical potentials and stoichiometric coefficients of the reactants and the reaction products, respectively. In the state of equilibrium, the chemical affinity is zero; for a reaction proceeding in the forward direction (in excess of reactants), this value is positive, while the reverse reaction (in excess of products) has a negative affinity.
Being an intensive variable (thermodynamic force), the chemical affinity determines an irreversible process related to a change in the composition of a system. In thermodynamics, this variable is considered jointly with the conjugated chemical variable 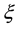 that is called the degree of completion of the reaction and is defined by the following relation [7] :
that is called the degree of completion of the reaction and is defined by the following relation [7] :
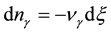 , (3)
, (3)
where 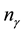 is the amount (number of moles) of component
is the amount (number of moles) of component . Upon dividing both parts of relation (3) by time increment
. Upon dividing both parts of relation (3) by time increment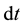 , we obtain an expression for the rate of variation of the number of moles
, we obtain an expression for the rate of variation of the number of moles 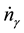 and the reaction rate
and the reaction rate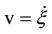 :
:
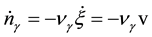
Introduction of the chemical affinity and the chemical variable into consideration allows one to reduce the number of variables 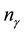
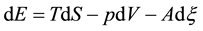
and the variation of entropy S is expressed as
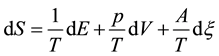
Here, the sum of the first and second terms on the right-hand side represents a reversible change in the entropy 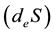
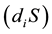
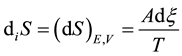
and the corresponding positive definite entropy production [7] :
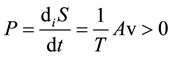
It turns out that, in the state of chemical equilibrium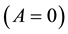
First, let consider the definition of the density of energy levels of a closed system in quantum statistics [5] . According to this, parameter D is defined as the ratio of the energy interval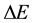
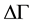
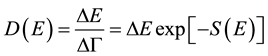
where 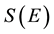
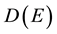
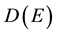
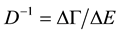
Since the chemical affinity is a linear combination of chemical potentials 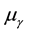
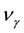
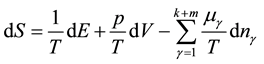
From Equation (9) we obtain the following expression for the chemical potential:
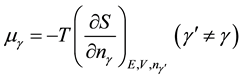
Using the quantum-statistical definition of entropy on the energy scale of temperature [5] ,
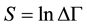
and taking into account expression (10), we obtain the following relation:
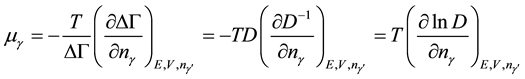
Not that, in deriving relation (11) at the stage of replacement of the statistical weight 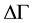
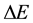
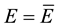
Now let us proceed to calculations of the chemical affinity (A) and total entropy production (P) using the quantum-statistical expression for the chemical potential (11) and formulas (4) and (7). For the chemical affinity, this yields
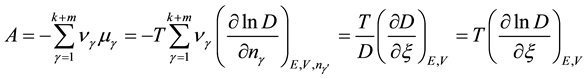
Note that, in deriving relation (12) at the stage of passing from variables 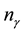
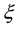

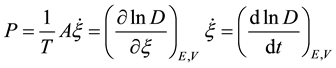
Since the chemical affinity of a system upon attaining the state of equilibrium is A = 0, relation (12) with allowance for nonzero absolute temperature T shows that
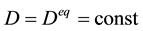
3. Conclusion
It follows from formula (13) that the positive constant parameter D, as expressed by Equation (14), corresponds to zero total entropy production and (in view of its being non-negative) to the absolute minimum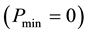

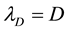
Cite this paper
M. B.Saikhanov, (2015) Chemical Affinity and the Density of Energy Levels. Journal of Modern Physics,06,1452-1455. doi: 10.4236/jmp.2015.611149
References
- 1. De Donde, Th. and Van Rysselberghe, P. (1936) Thermodynamic Theory of Affinity. Stanford University Press, Stanford University, Stanford.
- 2. Defay, R., Prigogine, I. and Bellemans, A. (1966) Surface Tension and Adsorption. Longman, London.
- 3. Prigogine, I. (1980) From Being to Becoming: Time and Complexity in the Physical Sciences. Freeman.
- 4. Planck, M. (1925) Sitzungsber. Acad. Wiss., Berlin.
- 5. Landau, L.D. and Lifshitz, E.M. (1980) Course of Theoretical Physics. Vol. 5, Statistical Physics, Butterworth-Heinemann, Oxford.
- 6. Saikhanov, M.B. (2012) International Journal of Modern Physics B, 26, Article ID: 1241005.
- 7. Prigogine, I. (1961) Introduction to Thermodynamics of Irreversible Processes. Interscience, New York.
- 8. Saikhanov, M.B. (2006) Russian Journal of Physical Chemistry A, 80, 1170-1171.
http://dx.doi.org/10.1134/S0036024406070314

