Journal of Modern Physics
Vol.06 No.08(2015), Article ID:57860,20 pages
10.4236/jmp.2015.68107
Photon Structure Function Revisited
Christoph Berger
I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
Email: berger@rwth-aachen.de
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 June 2015; accepted 7 July 2015; published 10 July 2015
ABSTRACT
The flux of papers from electron positron colliders containing data on the photon structure function
 ended naturally around 2005. It is thus timely to review the theoretical basis and confront the predictions with a summary of the experimental results. The discussion will focus on the increase of the structure function with x (for x away from the boundaries) and its rise with
ended naturally around 2005. It is thus timely to review the theoretical basis and confront the predictions with a summary of the experimental results. The discussion will focus on the increase of the structure function with x (for x away from the boundaries) and its rise with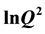 , both characteristics being dramatically different from hadronic structure functions. The agreement of the experimental observations with the theoretical calculations is a striking success of QCD. It also allows a new determination of the QCD coupling constant
, both characteristics being dramatically different from hadronic structure functions. The agreement of the experimental observations with the theoretical calculations is a striking success of QCD. It also allows a new determination of the QCD coupling constant
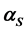 which very well corresponds to the values quoted in the literature.
which very well corresponds to the values quoted in the literature.
Keywords:
Structure Functions, Photon Structure, Two Photon Physics, QCD, QCD Coupling Constant

1. Historical Introduction
The notion that hadron production in inelastic electron photon scattering can be described in terms of structure functions like in electron nucleon scattering is on first sight surprising because photons are pointlike particles whereas nucleons have a radius of roughly 1 fm. Nevertheless the concept makes sense, not because the photon consists of pions, quarks, gluons etc., but because it couples to other particles and thus can fluctuate e.g. into a quark antiquark pair or a
 meson. These two basic processes are distinguished by the terms pointlike and hadronic throughout the paper. The idea of a photon fluctuating into a
meson. These two basic processes are distinguished by the terms pointlike and hadronic throughout the paper. The idea of a photon fluctuating into a
 meson or other vector mesons was soon applied to estimate the inelastic
meson or other vector mesons was soon applied to estimate the inelastic
 scattering cross section in the vector meson dominance model [1] [2] . Calculating the structure function in the quark model [3] then opened the intriguing possibility to investigate experimentally a structure function rising towards large x and showing a distinctive scale breaking because of the proportionality to
scattering cross section in the vector meson dominance model [1] [2] . Calculating the structure function in the quark model [3] then opened the intriguing possibility to investigate experimentally a structure function rising towards large x and showing a distinctive scale breaking because of the proportionality to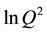 .
.
Excitement rose after the first calculation of the leading order QCD corrections, because Witten [4] not only calculated the markedly different x dependence of the structure function in QCD but demonstrated that the QCD parameter
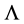 could in principle be determined by measuring an absolute cross section quite in contrast to lepton nucleon scattering, where small scale breaking effects in the
could in principle be determined by measuring an absolute cross section quite in contrast to lepton nucleon scattering, where small scale breaking effects in the
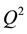 evolution of the structure function have to be studied. This “remarkable result” [5] initiated intensive discussions between theorists and experimentalists and passed the first experimental test [6] with flying colors. QCD calculations at next to leading order [7] [8] allowed to give
evolution of the structure function have to be studied. This “remarkable result” [5] initiated intensive discussions between theorists and experimentalists and passed the first experimental test [6] with flying colors. QCD calculations at next to leading order [7] [8] allowed to give
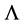 a precise meaning in the
a precise meaning in the
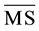 renormalization scheme, but also revealed a sickness of the absolute perturbative calculation, producing negative values of
renormalization scheme, but also revealed a sickness of the absolute perturbative calculation, producing negative values of
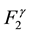 near
near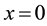 .
.
In an invited talk at the 1983 Aachen conference on photon photon collisions [9] , the audience was warned that the implications of these discoveries for the experimental goal of a direct determination of
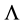 from
from
 were not altogether positive despite “the almost incredible advances on the experimental side”. Instead it was recommended to utilize the
were not altogether positive despite “the almost incredible advances on the experimental side”. Instead it was recommended to utilize the
 evolution like in deep inelastic scattering, a program which was also pursued by other groups [10] .
evolution like in deep inelastic scattering, a program which was also pursued by other groups [10] .
Ten years later an algebraic error in the original calculation [7] was discovered. Correcting this error [11] [12] squeezed the negative spike near

A new approach to follow the original goal [14] showed promising results. However, based on the results of [15] [16] the structure function for virtual photons was calculated [17] in next-to-next-to-leading-order (NNLO). The findings of this investigation forces one to the conclusion that an absolute prediction for the structure function of real photons is unstable at the three loop level. The concern of the 1980’s is thus still valid, albeit at a higher order in the perturbative series.
2. Basics
Deep-inelastic electron-photon scattering at high energies

is characterized by a large momentum transfer Q of the scattered electron and a large invariant mass W of the hadrons. The electron energies







are the essential variables for discussing the dynamics of the scattering process as can be seen from the cross section formula corresponding to Figure 1

which depends on the two structure functions







(with



For QED processes

Figure 1. Electron-photon scattering [generic Feynman diagram]. The incoming target photon g splits into a nearly collinear quark-antiquark pair. In QCD, the momentum of the internal quark line is reduced by gluon radiation. The impinging electron is scattered off the quark to large angles, the scatter pattern revealing the internal quark structure of the photon. Quark, anti- quark and gluons finally fragment to hadrons.
direction of the incoming photon and the other is scattered at large angels (balancing the transverse momentum of the outgoing electron) the structure function


with





For heavy quarks with three colors, fractional charge eq and masses







where






as the quark model or zero order QCD expression1 for the photon structure function if only light quarks are considered.
Using the general quark model relation

connecting structure function and quark densities


with

The factor 2 in Equation (12) accounts for the fact that the photon contains quarks and antiquarks with equal densities but the sum runs over quarks only.
3. QCD Predictions
3.1. Introduction, Leading Order Calculations
The first QCD analysis of the photon structure function [4] based on the operator product expansion (OPE) gave a unified picture of the hadronic and pointlike pieces including gluon radiation in leading order. It was shown that the x and





The nth Mellin moment of a function


For example, the quark model function


Like in DIS the quark densities are grouped into two classes described by different evolution equations, flavor non-singlet ( NS) and singlet (S):

where








analogous but not identical to the convention defined by Equation (12). Because of the factor x in Equation (18) the moments of the structure function are related to the moments of the quark densities by

or


We start with a discussion of the LO result for the pointlike

with

and


with


and










Similar (albeit more complicated) relations hold for

with

and


The dependence of




All splitting terms






with

A very useful combination of the results obtained so far is given by

where



Setting




with

The splitting functions





where m is now a continuous complex variable and the contour c has to lie on the right hand side of the rightmost singularity in
In practice, instead of inverting



were chosen because the shape of the corresponding valence and sea distributions in x-space is quite different. The pointlike LO solution in x-space is then given by

We focus on the asymptotic solution




pressions for

for








The results of both inversion methods agree very well, which is demonstrated in Figure 2, where




The coefficients necessary for calculating the asymptotic functions






Obviously the LO QCD calculation (37) preserves the



Figure 2. Asymptotic pointlike solutions for f = 3. Upper curve

Table 1. Coefficients needed to calculate the pointlike asymptotic contribution to



Figure 3. Red line: quark model (11) in units of



is compared to the evaluation of Equation (37) in units of
The fact that the





To complete the picture, Figure 3 also contains a QED like variant of the quarkmodel (10) with a log factor








Finally a careful inspection of the LO QCD result in Figure 3 reveals a small upward kink beginning at







any finite value of L the quotient


3.2. Next to Leading Order Calculations
In next to leading order the moments of the parton densities are changed, for example Equation (20) reads now

All NLO effects are contained in


(22). A similar relation holds for

densities, in NLO the quark model like relation Equation (19) between structure function and quark densities is also changed. Depending on the factorization scheme used, products of quark densities and the so called Wilson terms have to be added to the right hand side. The lengthy expressions needed to calculate the moments of the structure function in the


containing all NLO contributions in the last three terms on the right hand side.
For the numerical evaluation we prefer again to regroup all terms according to the valence and sea scheme. After inverting the moments the final equation describing the pointlike solution

is obtained. The strong coupling constant now has to be evaluated in NLO

with









Like in the LO case the structure of Equation (41) does not change if non asymptotic solutions are considered. One has then, however, for each pair of


Due to the negative correction













Figure 4. Comparison of the asymptotic pointlike structure func- tion in units of α at leading (green curve) and next to leading order (red curve) QCD for


A further example is studied in Figure 5 choosing





by the green curve. Due to an unfortunate algebraic error [7] the moments

1992 were not correct and resulted in a strongly negative sea term (black curve in Figure 5) which in turn led to a negative pointlike structure function already for

3.3. Master Formula and the Problem of Singularities
As already shown by Witten [4] the moments of the photon structrure function contain besides the pointlike
piece an additional term which in lowest order is written as




determines the moments of the structure function for





The pointlike terms can be rewritten as
Figure 5. Red curve: Asymptotic pontlike structure function in units of






The terms proportional to



be combined with the first term in (43) into a new hadronic contribution
with the



In this sum of hadronic terms and the asymptotic solution


We have shown this assumption to be valid for the LO and the NLO calculations. However in NNLO a completely different situation is to be faced. The most dangerous singularities originate now from NNLO terms





which leads in x-space to a divergent term





The principal problem of the poles of


luation of



3.4. Modelling the Hadroncic Piece of
The coupling of the photon to the final-state hadrons is mediated by quarks and antiquarks. If the transverse momentum




which is identical to the vector meson dominance (VMD) ansatz describing the hadronic nature of the photon

if the photon vector meson couplings




The result for







4. Two Photon Kinematics
Experiments measuring the photon structure function have until now only been performed at


is dominated by the so called two photon diagram shown in Figure 7 which also includes some kinematical definitions. Originally these reactions have been considered only as a background to

Figure 6. Shown is the x dependence of



Figure 7. Kinematics of the two photon process.


The incoming leptons in Figure 7 radiate virtual photons with four momenta

system X with an invariant mass


by a complicated combination of kinematical factors and six in principle unknown hadronic functions (four cross sections and two interference terms) depending on
In the limit


with


and

where the definition

The two photon cross sections


















Replacing the cross sections


we arrive after a change of variables at

which corresponds to Equation (4) multiplied by the spectral density of the incoming photons. Under actual experimental conditions, y is quite small in general, so that




The standard expression (53) has first been derived by Kessler [34] . In the spirit of the leading log appro- ximation it can be replaced by

useful for rough estimates of the counting rate. One has, however, to keep in mind that neglecting the cutoff







The basic experimental procedure is thus given by investigating the reaction






5. Experimental Analysis
Following the pioneering work of the PLUTO collaboration [6] many experiments have been performed at all high energy






After the 1980 crisis of the perturbative calculation most QCD analyses were performed like in deep inelastic scattering by comparing the data to models obtained by evolving the parton densities from a starting scale








Here we follow a more radical approach and fit the whole sample of 109 data sets to a model whose three components have been discussed in the previous sections:
1) The pointlike asymptotic NLO QCD prediction for 3 light flavors in the


2) A quark model calculation of the charm and bottom quark contribution using Equation (7) multiplied by




3) A detailed parameterization (VMD) for the hadronic part of the structure function [30] including the


Fitting the data with this model results in a value of


Following the method explained in [55]











which agrees nicely with the DIS average


In order to visualize the impressive agreement between data and theory two examples are presented. In Figure 8 the PLUTO data [31] at 4.3 GeV2 (black crosses) and the OPAL data [48] at 39.7 GeV2 (blue crosses) are compared with our model. The data clearly do not follow the typical mesonic


Next the










piece the theoretical model can in LO be written as
Figure 9 according to this ansatz yields


Figure 8. Dependence of

Figure 9. Dependence of






6. Virtual Photon Structure
The perturbative calculations have been extended to the region




Gluon radiation is efficiently suppressed for virtual photons, thus moving

model result. Analytically this can be proven easily [57] by investigating the LO order solution, e.g.



Using




i.e. the quark model formula (34) with the log factor replaced by





Regarding the determination of

that the virtual photon photon scattering is in general described by four cross sections and two interference terms
Figure 10. Dependence on x of the virtual photon structure function




Figure 11. Shown is the x dependence of




(see Section IV). After proper integration over the interference terms the cross section formula of [18] can be written as

where the factor




The relation between structure functions and cross sections is more complicated than discussed above for electron scattering off real photons. In the limit


using



one gets finally

Experimental data is scarce. The first results of the PLUTO collaboration [60] at




For comparison with theory




LO and NLO [17] [58] . Here we combine the LO result with the NLO calculation of the pointlike and hadronic terms. The charm quark contribution for



part was added multiplied by a form factor



form factor the VMD term is reduced by a factor 2.5 and thus for the sake of simplicity the straight line model

7. Conclusions
Measurements of the photon structure function









New experimental input can only be expected from a new high energy

Acknowledgements
First of all, I want to thank P.M. Zerwas for his constant support and the many discussions concerning the theoretical basis. I am very grateful for the help I got from R. Nisius. Useful conversations with M. Klasen are also gratefully acknowledged.
Cite this paper
ChristophBerger, (2015) Photon Structure Function Revisited. Journal of Modern Physics,06,1023-1043. doi: 10.4236/jmp.2015.68107
References
- 1. Walsh, T.F. (1971) Physics Letters B, 36, 121-123. http://dx.doi.org/10.1016/0370-2693(71)90124-9
- 2. Brodsky, S.J., Kinoshita, T. and Terazawa, H. (1971) Physical Review Letters, 27, 280-283.
http://dx.doi.org/10.1103/PhysRevLett.27.280 - 3. Walsh, T.F. and Zerwas, P.M. (1973) Physics Letters B, 44, 195-198.
http://dx.doi.org/10.1016/0370-2693(73)90520-0 - 4. Witten, E. (1977) Nuclear Physics B, 120, 189-202.
http://dx.doi.org/10.1016/0550-3213(77)90038-4 - 5. Llewellyn-Smith, C.H. (1978) Physics Letters B, 79, 83-87.
http://dx.doi.org/10.1016/0370-2693(78)90441-0 - 6. PLUTO Collaboration, Berger, C., Genzel, H., Grigull, R., Lackas, W., Raupach, F., et al. (1981) Physics Letters B, 107, 168-172. http://dx.doi.org/10.1016/0370-2693(81)91174-6
- 7. Bardeen, W.A. and Buras, A.J. (1979) Physical Review D, 20, 166-178.
http://dx.doi.org/10.1103/PhysRevD.20.166 - 8. Duke, D.W. and Owens, J.F. (1980) Physical Review D, 22, 2280-2285.
http://dx.doi.org/10.1103/PhysRevD.22.2280 - 9. Duke, D.W. (1983) Photon Photon Collisions. In: Berger, C., Ed., Proceeding of the Fifth International Workshop on Photon Photon Collisions, Lecture Notes in Physics 191, Springer Verlag, Berlin, 251-269.
- 10. Glück, M. and Reya, E. (1983) Physical Review D, 28, 2749-2755.
http://dx.doi.org/10.1103/PhysRevD.28.2749 - 11. Glück, M., Reya, E. and Vogt, A. (1992) Physical Review D, 45, 3986-3994.
http://dx.doi.org/10.1103/PhysRevD.45.3986 - 12. Fontanaz, M. and Pilon, E. (1992) Physical Review D, 45, 382-384.
http://dx.doi.org/10.1103/PhysRevD.45.382 - 13. Antoniadis, I. and Grunberg, G. (1983) Nuclear Physics B, 213, 445-466.
http://dx.doi.org/10.1016/0550-3213(83)90230-4 - 14. Albino, S., Klasen, M. and Söldner-Rembold, S. (2002) Physical Review Letters, 89, Article ID: 122004.
http://dx.doi.org/10.1103/PhysRevLett.89.122004 - 15. Moch, S., Vermaseren, J.A.M. and Vogt, A. (2004) Nuclear Physics B, 688, 101-134.
http://dx.doi.org/10.1016/j.nuclphysb.2004.03.030 - 16. Vogt, A., Moch, S. and Vermaseren, J.A.M. (2004) Nuclear Physics B, 691, 129-181.
http://dx.doi.org/10.1016/j.nuclphysb.2004.04.024 - 17. Ueda, T., Sasaki, K. and Uematsu, T. (2007) Physical Review D, 75, Article ID: 114009.
http://dx.doi.org/10.1103/PhysRevD.75.114009 - 18. Budnev, V.M., Ginzburg, I.F., Meledin, G.V. and Serbo, V.G. (1975) Physics Reports, 15, 181-282.
http://dx.doi.org/10.1016/0370-1573(75)90009-5 - 19. DeWitt, R.J., Jones, L.M., Sullivan, J.D., Willen, D.E. and Wyld, H.W. (1979) Physical Review D, 19, 2046-2052.
http://dx.doi.org/10.1103/PhysRevD.19.2046 - 20. Frazer, W.R. and Gunion, J.F. (1979) Physical Review D, 20, 147-165.
http://dx.doi.org/10.1103/PhysRevD.20.147 - 21. Buras, A.J. (2006) Acta Physica Polonica B, 37, 609-617.
- 22. Floratos, E.G., Kounnas, C. and Lacaze, R. (1981) Nuclear Physics B, 192, 417-462.
http://dx.doi.org/10.1016/0550-3213(81)90434-X - 23. Peterson, C., Walsh, T.F. and Zerwas, P.M. (1980) Nuclear Physics B, 174, 424-444.
http://dx.doi.org/10.1016/0550-3213(80)90293-X - 24. Zerwas, P.M. (2014) Private Communication.
- 25. Peterson, C., Walsh, T.F. and Zerwas, P.M. (1983) Nuclear Physics B, 229, 301-316.
http://dx.doi.org/10.1016/0550-3213(83)90334-6 - 26. Berger, C. and Wagner, W. (1987) Physics Reports, 146, 1-134.
http://dx.doi.org/10.1016/0370-1573(87)90012-3 - 27. Rossi, G. (1983) Physics Letters B, 130, 105-108; http://dx.doi.org/10.1016/0370-2693(83)91073-0 Rossi, G. (1984) Physical Review D, 29, 852-868. http://dx.doi.org/10.1103/PhysRevD.29.852
- 28. Moch, S., Vermaseren, J.A.M. and Vogt, A. (2002) Nuclear Physics B, 621, 413-458.
http://dx.doi.org/10.1016/S0550-3213(01)00572-7 - 29. Glück, M., Reya, E. and Schienbein, I. (1999) Physical Review D, 60, Article ID: 054019.
http://dx.doi.org/10.1103/PhysRevD.60.054019 - 30. Glück, M., Reya, E. and Schienbein, I. (1999) The European Physical Journal C, 10, 313-317.
http://dx.doi.org/10.1007/s100529900124 - 31. PLUTO Collaboration, Berger, C., Deuter, A., Genzel, H., Lackas, W., Pielorz, J., et al. (1984) Physics Letters B, 142, 111-118. http://dx.doi.org/10.1016/0370-2693(84)91145-6
- 32. Schienbein, I. (2002) Annals of Physics, 301, 128-156. http://arxiv.org/abs/hep-ph/0205301
- 33. Berger, C. and Field, J.H. (1981) Nuclear Physics B, 187, 585-593.
http://dx.doi.org/10.1016/0550-3213(81)90477-6 - 34. Kessler, P. (1960) Il Nuovo Cimento, 17, 809-829. http://dx.doi.org/10.1007/BF02732124
- 35. Nisius, R. (2000) Physics Reports, 332, 165-317. http://dx.doi.org/10.1016/S0370-1573(99)00115-5
- 36. ALEPH Collaboration, Barate, R., Decamp, D., Ghez, P., Goy, C., Lees, J.-P., et al. (1999) Physics Letters B, 458, 152-166. http://dx.doi.org/10.1016/S0370-2693(99)00559-6
- 37. ALEPH Collaboration, Heister, A., Schael, S., Barate, R., Bruneliere, R., De Bonis, I., et al. (2003) The European Physical Journal C, 30, 145-158. http://dx.doi.org/10.1140/epjc/s2003-01291-4
- 38. AMY Collaboration, Sahu, S.K., Ebara, S., Nozaki, T., Behari, S., Fujimoto, H., Kobayashi, S., et al. (1995) Physics Letters B, 346, 208-216. http://dx.doi.org/10.1016/0370-2693(95)00092-Y
- 39. AMY Collaboration, Kojima, T., Nozaki, T., Abe, K., Fujii, Y., Kurihara, Y., Lee, M.H., et al. (1997) Physics Letters B, 400, 395-400. http://dx.doi.org/10.1016/S0370-2693(97)00349-3
- 40. DELPHI Collaboration, Abreu, P., Agasi, E.E., Augustinus, A., Hao, W., Holthuizen, D.J., Kluit, P.M., et al. (1996) Zeitschrift für Physik C, 69, 223-233. http://dx.doi.org/10.1007/s002880050022
- 41. JADE Collaboration, Bartel, W., et al. (1984) Zeitschrift für Physik C, 24, 231-283.
- 42. L3 Collaboration, Acciarri, M., Adriani, O., Aguilar-Benitez, M., Ahlen, S., Alcaraz, J., Alemanni, G., et al. (1998) Physics Letters B, 436, 403-416. http://dx.doi.org/10.1016/S0370-2693(98)01025-9
- 43. L3 Collaboration, Acciarri, M., Achard, P., Adriani, O., Aguilar-Benitez, M., Alcaraz, J., Alemanni, G., et al. (1999) Physics Letters B, 447, 147-156. http://dx.doi.org/10.1016/S0370-2693(98)01552-4
- 44. L3 Collaboration, Acciarri, M., Achard, P., Adriani, O., Aguilar-Benitez, M., Alcaraz, J., Alemanni, G., et al. (2000) Physics Letters B, 483, 373-386. http://dx.doi.org/10.1016/S0370-2693(00)00587-6
- 45. L3 Collaboration, Achard, P., Adriani, O., Aguilar-Benitez, M., Alcaraz, J., Alemanni, G., Allaby, J., et al. (2005) Physics Letters B, 622, 249-264. http://dx.doi.org/10.1016/j.physletb.2005.07.028
- 46. OPAL Collaboration, Ackerstaff, K., Alexander, G., Allison, J., Altekamp, N. and Ametewee, K. (1997) Zeitschrift für Physik C, 74, 33-48. http://dx.doi.org/10.1007/s002880050022
- 47. OPAL Collaboration, Ackerstaff, K., Alexander, G., Allison, J., Altekamp, N., Anderson, K.J., Anderson, S., et al. (1997) Physics Letters B, 411, 387-401. http://dx.doi.org/10.1016/S0370-2693(97)01023-X
- 48. OPAL Collaboration, Abbiendi, G., Ainsley, C., Åkesson, P.F., Alexander, G., Allison, J., Anagnostou, G., et al. (2002) Physics Letters B, 533, 207-222. http://dx.doi.org/10.1016/S0370-2693(02)01560-5
- 49. PLUTO Collaboration, Berger, C., Genzel, H., Lackas, W., Pielorz, J., Raupach, F., Wagner, W., et al. (1987) Nuclear Physics B, 281, 365-380. http://dx.doi.org/10.1016/0550-3213(87)90410-X
- 50. TASSO Collaboration, Althoff, M., Braunschweig, W., Gerhards, R., Kirschfink, F.J., Martyn, H.U., Rosskamp, P., et al. (1986) Zeitschrift für Physik C, 31, 527-535.
http://dx.doi.org/10.1007/BF01551073 - 51. TOPAZ Collaboration, Muramatsu, K., Hayashii, H., Noguchi, S., Fujiwara, N., Abe, K., Abe, T., et al. (1994) Physics Letters B, 332, 477-487. http://dx.doi.org/10.1016/0370-2693(94)91284-X
- 52. TPC/2γ Collaboration, Aihara, H., et al. (1987) Zeitschrift für Physik C, 34, 1-13.
- 53. Cornet, F., Jankowski, P. and Krawczyk, M. (2004) Physical Review D, 70, Article ID: 093004. http://dx.doi.org/10.1103/PhysRevD.70.093004
- 54. Particle Data Group, Beringer, J., et al. (2012) Physical Review D, 86, Article ID: 010001.
http://pdg.lbl.gov/2012/listings/contents_listings.html - 55. Marciano, W.J. (1984) Physical Review D, 29, 580-591. http://dx.doi.org/10.1103/PhysRevD.29.580
- 56. Bethke, S. (2012) http://arxiv.org/pdf/1210.0325.pdf
- 57. Uematsu, T. and Walsh, T.F. (1981) Physics Letters B, 101, 263-266.
http://dx.doi.org/10.1016/0370-2693(81)90309-9 - 58. Uematsu, T. and Walsh, T.F. (1982) Nuclear Physics B, 199, 93-118.
http://dx.doi.org/10.1016/0550-3213(82)90568-5 - 59. Laenen, E., Riemersma, S., Smith, J. and van Neerven, W.L. (1994) Physical Review D, 49, 5753-5768.
http://dx.doi.org/10.1103/PhysRevD.49.5753 - 60. PLUTO Collaboration, Berger, C., Deuter, A., Genzel, H., Lackas, W., Pielorz, J., Raupach, F., et al. (1984) Physics Letters B, 142, 111-118. http://dx.doi.org/10.1016/0370-2693(84)91145-6
- 61. ILC Collaboration, Bagger, J., et al. (2014) The International Linear Collider, Gateway to the Quantum Universe Committee. http://www.linearcollider.org/pdf/ilc_gateway_report.pdf
- 62. Muhlleitner, M.M. and Zerwas, P.M. (2006) Acta Physica Polonica B, 37, 1021-1038.
http://arxiv.org/abs/hep-ph/0511339 - 63. Sasaki, K., Ueda, T., Kitadono, Y. and Uematsu, T. (2007) PoS RADCOR2007, 035.
http://arxiv.org/abs/0801.3533
NOTES
1A solution which formally requires very high



2This formula also demonstrates drastically how the introduction of a second scale destroys the sensitivity to






















