Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57049,5 pages
10.4236/jmp.2015.67090
How Does Wave Packet of a Free Particle Yield?
Tianhai Zeng
School of Physics, Beijing Institute of Technology, Beijing, China
Email: zengtianhai@bit.edu.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 April 2015; accepted 8 June 2015; published 11 June 2015
ABSTRACT
Preparing a particle in a superposition or a wave packet of eigenstates of a physical quantity is to let it interact with a large object. The composite system composed of the particle and the large object evolves into an entangled state. When the state of the large object is considered to be approximately unchanged, the entangled state can be approximately considered as a product state, and then the particle is prepared in an approximate superposed state. We consider the Schrödinger equation for a composite system with interactions between subsystems as a fundamental postulate and a single particle’s Schrödinger equation must be approximately obtained from it. We argue that superposition of states exists only in composite systems. Interaction exchanging some quantities between subsystems makes conservation laws strictly hold, and no wave packet of a free particle yields. With this point, we can also understand the double-slit experiment and the tunnel phenomenon.
Keywords:
Superposition of Eigenstates, Interaction, Entangled State, Conservation Law, Double-Slit Experiment, Tunnel Phenomenon

1. Introduction
According to the measurement postulate in quantum mechanics [1] -[3] , if a free particle is initially in a superposition or a wave packet of energy (that is kinetic energy) eigenstates and its energy is measured, its state will collapse into an energy eigenstate. In accordance with the Schrödinger equation for a free particle, an energy eigenstate never automatically evolves into a superposition or a wave packet of energy eigenstates, though an energy eigenstate and a superposition of eigenstates (SE) of energy are both solutions of the Schrödinger equation. This can be explained in Figure 1.
For a pair of incompatible observables for a free particle, the corresponding operators do not commute with each other and have not shared eigenstates (or eigenfunctions). An eigenstate of one observable seems naturally to be the SE of the other since it is easily expanded in other eigenstates mathematically, but the general way in physics is to let it interact with other large object (LO, explained in Section 2), for example, a particle interacting with a double-slit, a photon interacting with a beam splitter, an electron interacting with a Stern-Gerlach apparatus. According to the viewpoint of Einstein et al. [4] , the interaction (INT) makes a particle and a LO evolve into an entangled state, which was termed by Schrödinger [5] . The entangled state maintains its entanglement even after the INT ceases in the viewpoint of non-locality [6] . Strictly, the particle is not in a SE.
The example of quantities momentum 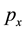 and coordinate x is different from the above cases. When a free particle is in an eigenstate of
and coordinate x is different from the above cases. When a free particle is in an eigenstate of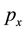 , x always changes; the eigenstate seems to be a SE of x. We argue that if we consider the eigenstate to be a SE of x, then a macro-object in motion with
, x always changes; the eigenstate seems to be a SE of x. We argue that if we consider the eigenstate to be a SE of x, then a macro-object in motion with 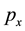 is also in a SE of x. However, a macro-object is not in any SE. Hence, an eigenstate of
is also in a SE of x. However, a macro-object is not in any SE. Hence, an eigenstate of 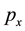 of a free particle should not be considered as a SE of x, that is, an eigenstate of one observable should not be considered as the SE of the other.
of a free particle should not be considered as a SE of x, that is, an eigenstate of one observable should not be considered as the SE of the other.
We ponder how a state of a free particle can return to its initial SE of a physical quantity after the SE has collapsed into an eigenstate following a measurement. To our knowledge, there is little information available in literature about this. Here, we discuss this issue. We think when the state of the LO is considered in some approximation to be unchanged, the entangled state can be approximately considered as a product state, and then the particle is prepared in an approximate superposed state. We explain this in Figure 2.
In Section 2, we introduce two examples to explain the way to prepare a superposition of atomic ground and an excited states starting from one of them. Conservation laws are explained in the Section. In Section 3, we consider the Schrödinger equation for a composite system as a fundamental postulate and approximately obtain a single particle’s Schrödinger equation. Section 4 gives out our understandings about some quantum phenomena. Conclusions are in the Section 5.
2. Prepare Superposition of Atomic Ground and Excited States
Haroche and his colleagues [7] prepared a superposition of two energy eigenstates of an atom starting from its ground state 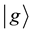 or its excited state
or its excited state . They let the atom interact with a beam splitter (a microwave pulse in a coherent state
. They let the atom interact with a beam splitter (a microwave pulse in a coherent state 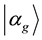 or
or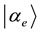 ), and created a combined atom + beam splitter state as an entangled state, which cannot be expressed in factored form, i.e.,
), and created a combined atom + beam splitter state as an entangled state, which cannot be expressed in factored form, i.e.,  of a new state
of a new state 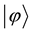 of the atom and a new state
of the atom and a new state 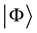 of the
of the
beam splitter. Specifically, this entangled state is expressed by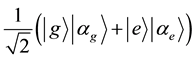 , and the mean number
, and the mean number
of photons for the two coherent states satisfy  , signifying that the atom exchanges a single photon with the beam splitter by the INT. Haroche et al. considered
, signifying that the atom exchanges a single photon with the beam splitter by the INT. Haroche et al. considered 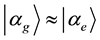 in the classical limit [7] , but they did not give the following approximate Equation (1). We write the entangled state as
in the classical limit [7] , but they did not give the following approximate Equation (1). We write the entangled state as
 (1)
(1)
Figure 1. An energy eigenstate never automatically evolves into a superposition of energy eigenstates according to Schrödinger equation for a free particle.
Figure 2. One, who made the mathematical expansion, easily omits the real physical process.
The entangled state can be approximately considered as a product state and thereby the approximate SE or the
simplest wave packet of the levels, 
In quantum optics, when an atom initially in the ground state 
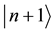



means the atom exchanges a photon with the single-mode field by the INT. When n is large enough, then

The entangled state can also be approximately considered as a product state and the atom is said to be in an approximate SE and is not free either.
If the atomic state collapses into the state 


energies are different from each other. Therefore, energy conservation does not hold for this atomic process and the state is only considered to carry statistical information. When we consider that the entangled state of the CS collapses into the state 

We consider the INT between a particle and a LO (strong field, a large or macro apparatus) is a reasonable and helpful way to understand why particles may be in SEs. This is familiar in two instances; one is momentum exchange, considered by Bohr [6] , where an exchange of momentum takes place between a particle passing through a slit in a diaphragm and the diaphragm, and the other is decoherence [9] , in which a quantum system is entangled with the environment and the unavoidable INT between them then destroys the coherence among its states. We suggest the mass ratio for a proton and electron, ~1836, or, depending on a specific case, some other constant, as a determining criterion in deciding when to neglect the change of a state of one object in a CS. For example, if the mass, energy or magnitude of momentum, of the object is 1836 times that of the particle, as for the proton in a hydrogen atom, we may then treat such an object as a large object (LO).
3. Consider the Schrödinger Equation for a Composite System as a Fundamental Postulate
We consider the Schrödinger equation for a CS with INTs between subsystems as a fundamental postulate. There always exists the INT between a considered particle and other object. A free particle does not exist. Single particle’s Schrödinger equation must be approximately obtained from that of a CS composed of the particle and other LO with INT between them. The Schrödinger equation of the CS is

where 


(potential) energy belonging to the CS. The CS state 
We can use kinetic energy eigenstates of the LO to expand the CS state

4. Understandings of Some Quantum Phenomena
When an electron in a spin state 


where 









A similar inference can be said for a photon polarized state or a photon path state. When a photon interacts with a beam splitter and the state of the beam splitter is approximately considered to be unchanged, its state may be resolved approximately into a superposition of polarized states or path states.
The most typical of quantum phenomena is considered to be the double-slit interference of material particles. Feynman [10] said that no one has found any machinery to explain it and no one will give you any deeper representation of the situation. We try to explain the interference in the following. We can set aside the idea of a particle passing through the two slits as a wave and suppose that a single particle passes through one slit of the double-slit (the time


where 









In the symmetric case, 

where two coefficients (1/2) express a particle passing through each slit with a half probability. Since


evolve approximately into the same superposed state
the particle source or double-slit perpendicular to the slits and the line of the source to the “center” of slits, we guess that the density operator should be as

where
In [11] , the authors describe weak measurements of single photons passing through a double-slit apparatus and obtained ‘trajectories’ which represent the average behavior of the ensemble of measured photons. Their results showed that when the distance of the screen to the double-slit increases, the interference pattern changes from being two bright fringes to one having several bright fringes symmetrically arranged about a central bright fringe. We can employ the above Equation (7) to explain the interference pattern changes better than employing
the single superposition
and is used to explain double-slit interference patterns in general, because the latter cannot be used to explain well the interference pattern (not appearing one bright fringe in center, but appearing two bright fringes symmetrically) near double-slit.
If the path of a particle passing through a slit is measured, the initial path state of a particle passing through slit 1 (2) is not 


In recent papers [12] -[17] , the authors considered the INT between a particle and a micro-object forming the double-slit in their calculations, and obtained the results agreeing with their experimental ones. The first case [12] -[15] is that the double-slit is larger than the projectile particle (electron). Their calculations include the INT between a projectile particle and the double-slit in Schrödinger’s equation or Hamiltonian, and neglect the kinetic energy operator of the double-slit. The second case [16] [17] is that the double-slit is even smaller than the projectile particle, so their calculations must include the kinetic energy operator of the double-slit, and the projectile particle cannot be approximately in a SE. Therefore, it is reasonable that we consider the INT between a particle and a macro-double-slit and the CS evolving into an entangled state.
The tunnel phenomenon can be explained as following. The barrier potential is actually the INT energy between a particle and a large object, the CS evolves into an entangled state, the energy of a particle may surpass with a probability the barrier potential due to INT exchanging energy between the particle and the large object. Therefore we can understand that the particle passes over with a part of the probability, the particle maintaining the incident direction, the barrier naturally, and does not penetrate the barrier.
5. Conclusions
The principle of superposition of states (one state may be an eigenstate or a SE) in quantum mechanics [1] -[3] [18] is that a superposition with two or more different states of a particle (or a system) is still its state, and the principle is independent of INT. However, we believe that SEs exist only in CSs with INTs between subsystems and are entangled states. INTs and conservation laws should also be restrictive conditions on the entangled states. The physical meaning of conservation laws is that the corresponding physical quantities are exchanged by INTs between subsystems, such as energy and momentum, and the quantities (scalars or vectors) are conserved no matter into what state the entangled state collapses, as explained in the examples, Equations (1) and (2). If the INT ceases, then we think that no quantities are exchanged between subsystems, so the entangled state is disentangled and no such superposition, right hands of Equations (1) and (2), of a free particle can be obtained.
The SE may be considered as a core feature of the wave. If there is no INT, a free particle will not be in a SE, and hence will not display wave-like properties. A de Broglie wave-vector and frequency can only be considered as parameters corresponding to a definite momentum and energy of a free particle, respectively. In the original concept of wave-particle duality in quantum mechanics, the wave and particle properties of a particle are intrinsic and the wave property is not related to any INT. Because INTs exist everywhere, our proposed concept¾that the wave property of a particle and the principle of superposition of states are related to INT¾may be a better choice than that encountered in conventional quantum mechanics.
Acknowledgements
I thank Shou-Yong Pei, Jian Zou, Bin Shao, Feng Wang, Xiu-San Xing, Jun-Gang Li, Xiang-Dong Zhang, Yu-Gui Yao, Jin-Fang Cai, Rui Wang, Chang-Hong Lu, Wen-Yong Su and Fan Yang for enlightening discussions and comments, Hao Wei, Li-Fan Ying, Gui-Qin Li and Yong-Jun Lu for help, and Pei-Zhu Ding and Shou-Fu Pan for encouragement. The work was partly supported by the National Natural Science Foundation of China (Grant Nos. 11075013, and 11375025).
References
- Dirac, P.A.M. (2008) The Principle of Quantum Mechanics. Science Press, Beijing.
- Griffiths, D.J. (2005) Introduction to Quantum Mechanics. Prentice-Hall, Inc., Upper Saddle River.
- Shankar, R. (1994) Principles of Quantum Mechanics. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4757-0576-8
- Einstein, A., Podolsky, B. and Rosen, N. (1935) Physical Review, 47, 777-780. http://dx.doi.org/10.1103/PhysRev.47.777
- Wheeler, J.A. and Zurek, W.H. (1983) Quantum Theory and Measurement. Princeton University Press, Princeton. http://dx.doi.org/10.1515/9781400854554
- Bohr, N. (1935) Physical Review, 48, 696-702. http://dx.doi.org/10.1103/PhysRev.48.696
- Bertet, P., Osnaghi, S., Rauschenbeutel, A., Nogues, G., Auffeves, A., et al. (2001) Nature, 411, 166-170. http://dx.doi.org/10.1038/35075517
- Walls, D.F. and Milburn, G.J. (1994) Quantum Optics. Springer-Verlag, Berlin Heidelberg. http://dx.doi.org/10.1007/978-3-642-79504-6
- Zurek, W.H. (2003) Reviews of Modern Physics, 75, 715-775. http://dx.doi.org/10.1103/RevModPhys.75.715
- Feynman, R.P. (2004) The Feynman Lectures on Physics. Vol. 8, Pearson Education Asia Limited and Beijing World Publishing Corporation, Hong Kong, Beijing.
- Kocsis, S., Braverman, B., Ravets, S., Stevens, M.J., Mirin, R.P., Shalm, L.K. and Steinberg, A.M. (2011) Science, 332, 1170-1173. http://dx.doi.org/10.1126/science.1202218
- Akoury, D., Kreidi, K., Jahnke, T., Weber, T., Staudte, A., Schoffler, M., et al. (2007) Science, 318, 949-952. http://dx.doi.org/10.1126/science.1144959
- Liu, X.J., Miao, Q., Gel’mukhanov, F., Patanen, M., Travnikova, O., Nicolas, C., et al. (2014) Nature Photonics, 9, 120- 125. http://dx.doi.org/10.1038/nphoton.2014.289
- Kushawaha, R.K., Patanen, M., Guillemin, R., Journel, L., Miron, C., Simon, M., et al. (2013) Proceedings of the National Academy of Sciences of the United States of America, 110, 15201-15206. http://dx.doi.org/10.1073/pnas.1306697110
- Cherepkov, N.A., Semenov, S.K., Schöffler, M.S., Titze, J., Petridis, N., Jahnke, T., et al. (2010) Physical Review A, 82, Article ID: 023420. http://dx.doi.org/10.1103/PhysRevA.82.023420
- Schmidt, L.P.H., Lower, J., Jahnke, T., Schößler, S., Schöffler, M.S., Menssen, A., et al. (2013) Physical Review Letters, 111, Article ID: 103201. http://dx.doi.org/10.1103/PhysRevLett.111.103201
- Schmidt, L.P.H., Schössler, S., Afaneh, F., Schöffler, M., Stiebing, K.E., Schmidt-Böcking, H. and Dörner, R. (2008) Physical Review Letters, 101, Article ID: 173202. http://dx.doi.org/10.1103/PhysRevLett.101.173202
- Landau, L.D. and Lifshitz, E.M. (1977) Quantum Mechanics. Pergamon Press Ltd., Oxford.



