Journal of Modern Physics
Vol.06 No.12(2015), Article ID:60108,5 pages
10.4236/jmp.2015.612175
Alternative Derivation of the Mean-Field Equations for Composite Fermions
Edmundo C. Manavella1,2, Carlos E. Repetto1,2
1Instituto de Física Rosario (CONICET-UNR), Rosario, Argentina
2Facultad de Ciencias Exactas, Ingeniería y Agrimensura (UNR), Rosario, Argentina
Email: manavella@ifir-conicet.gov.ar, repetto@ifir-conicet.gov.ar
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 March 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
The Hamiltonian describing a composite fermion system is usually presented in a phenomenological way. By using a classical nonrelativistic U(1) × U(1) gauge field model for the electromagnetic interaction of electrons, we show how to obtain the mean-field Hamiltonian describing composite fermions in 2 + 1 dimensions. In order to achieve this goal, the Dirac Hamiltonian formalism for constrained systems is used. Furthermore, we compare these results with the ones corresponding to the inclusion of a topological mass term for the electromagnetic field in the Lagrangian.
Keywords:
Quantum Field Theory, Field Theories in Dimensions Other than Four, Chern-Simons Gauge Theory, Lagrangian and Hamiltonian Formalisms

1. Introduction
The study of low-dimensional electron systems is a topic of great current interest in condensed matter. Under certain conditions, three-dimensional solids can behave as pseudo two or one-dimensional quantum systems. Among other things, this is because these systems have special characteristics which lead to phenomena such as superconductivity of high critical temperature and some magnetic properties, with potential technological applications.
Since a long time ago, the phenomenon of high-temperature superconductivity is being considered with increasing interest. The current status of knowledge on this subject does not allow establishing on firm foundation this phenomenology. Different approaches are used to address this issue. A promising approach is based on models using composite particles [1] [2] . In Ref. [1] , Jain and Anderson propose the existence of an underlying connection between the resonating valence bond theory for high-temperature superconductivity and the composite fermion theory for the fractional quantum Hall effect [3] -[5] . Besides, in Ref. [2] , Lu, Das Sarma and Park relate the superconductivity with the quantum Hall effect through the formation of Cooper pairs of composite fermions.
A manner of studying these systems is based on quantum field theory. Another manner is to use quantum many-body theory [6] [7] , implemented by using analytical and computational techniques.
In Refs. [8] [9] , we have proposed models of composite particles and we have studied them by using the first mechanism cited in the previous paragraph. These models are generalizations of the models discussed by means of the second mechanism in Refs. [10] -[12] .
To deal with models that consider the electromagnetic interaction of composite fermions, a phenomenological Hamiltonian is commonly used. In this paper, by using the standard methods of field theory, we show that the same Hamiltonian can be reached.
In this context, our purpose is to relate the results of Refs. [8] [9] with the ones corresponding to Ref. [10] , by using the usual techniques of field theory. In particular, we use the Dirac Hamiltonian formalism for constrained systems. In this way, we show that this procedure leads to the same results as the ones obtained by means of the phenomenological models of condensed matter. For example, the Coulombian interaction density which appears in the standard formulation [10] is deduced from the formalism. Moreover, from the constraint structure, we determine the relation between the electron-density distribution and the magnetic flux quanta.
Besides, we show that the inclusion of a topological mass term for the electromagnetic field in the Lagrangian density introduces interaction terms absent in the original canonical Hamiltonian.
The paper is organized as follows. In Section 2, we show how to obtain the canonical Hamiltonian from the starting Lagrangian. Then, in Section 3, we see what happens when we add a topological mass term for the electromagnetic field in the Lagrangian. Finally, in Section 4, we display our conclusions.
2. Formalism
We consider a classical nonrelativistic field theory with U(1) × U(1) gauge symmetry in 2 + 1 dimensions for the electromagnetic interaction of electrons. This model uses a Chern-Simons (CS) U(1) gauge auxiliary field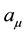 .
.
In order to describe this interaction, we propose the following singular Lagrangian density:
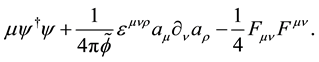 (1)
(1)
The Greek indices take the values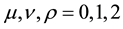 . We use natural units where
. We use natural units where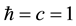 . The Minkowski metric is
. The Minkowski metric is 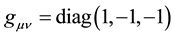 and
and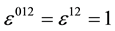 . The covariant derivative involving both the CS field and the electromagnetic field is written as
. The covariant derivative involving both the CS field and the electromagnetic field is written as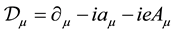 , and we design
, and we design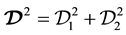 . Furthermore,
. Furthermore, 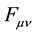 is the electromagnetic field tensor.
is the electromagnetic field tensor.
The matter field 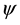 is a charged spinorial field which describes electrons with charge
is a charged spinorial field which describes electrons with charge 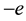 and band mass
and band mass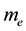 . The chemical potential of the electrons is
. The chemical potential of the electrons is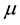 . The constant
. The constant 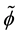 introduced in the Lagrangian density, will be determined later.
introduced in the Lagrangian density, will be determined later.
The independent dynamical field variables are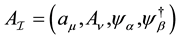 , and their corresponding canonically
, and their corresponding canonically
conjugate momenta, defined by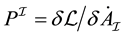 , are
, are
dices take the values
The canonical Hamiltonian density, defined as

where the Latin indices take the values
As usual, the relations between the fields and the momenta not depending on the velocities lead to primary constraints. Thus, the momentum 
Finally, classifying the total set of constraints, we find the first and second-class constraints. The first-class constraints are




while the second-class ones are



We choose the following gauge-fixing conditions, which are consistent with the equations of motion:




The algebraic development corresponding to these results were performed in Ref. [8] .
As it is well known, one can define the Dirac brackets from the Bose-Fermi ones, and then all the equations of the theory are formulated taking into account the former brackets, as it can be seen in Ref. [8] . Once we impose the Dirac brackets, the first and second-class constraints and the gauge-fixing conditions can be set strongly equal to zero. In this way, these equations become identities expressing some canonical variables in terms of the others, that is,







It is worth to mention that, in order to obtain Equation (15) from Equation (13), we have substituted the logarithmic interaction [9] , characteristic of a strict two dimensional space, by the standard Coulombian [13] . This is justified because the electrons are confined to move in two dimensions, but interact each other in a world of three dimensions.
By replacing the momenta of Equations (19) and (20) in Equation (4), we get

The term 
Taking the spatial derivative of the momentum 

In Ref. [10] , this equation is considered as a constraint of the theory. In the Lagrangian density (1), this constraint appears multiplied by
The curl of the CS field is linked with a magnetic field in the form
Therefore, the Lagrangian density (1) describes a composite fermion system, where 




Replacing all previous results in Equation (2), we obtain

where

Since the field 

with

where 

Besides, following Ref. [14] , but taking into account that we are working in 2 + 1 dimensions, the electric field can be split in its transversal and longitudinal components in the plane of electron motion



where B is perpendicular to the motion plane.
Finally, we can write

Usually, when only an external uniform magnetic field is considered, the canonical Hamiltonian reduces to

3. Addition of a Topological Mass Term for the Electromagnetic Field
As it is well known, the addition of the CS term to the Maxwell action leads to the topologically massive (2 + 1)-dimensional electrodynamics [15] . In this theory, a modified Gauss law appears. As a result, any charged particle carries a magnetic flux proportional to its charge.
In this section, we analyze the differences that appear with respect to the original model when a topological mass term for the electromagnetic field is added to the Lagrangian density 

where 

In this case, the canonical Hamiltonian density becomes

where 

The only first-class constrains that change with respect to the previous ones are


In the same way, the only gauge-fixing condition that changes is

These results have been formally demonstrated in Ref. [9] .
Following the same steps like in the previous section, it can be proved that the constraint (22) remains valid.
In contrast to Equation (15), 

Finally, the topological massive canonical Hamiltonian density is

By replacing 

where 
Once we integrate Equation (37), the first two terms give the same contributions to the Hamiltonian. By considering the constraint (22), these terms can be associated to the interaction between the external and CS magnetic fields mediated by the distance. In the limit of infinite topological mass, this interaction vanishes. This is consistent with the fact that in the usual formulation, where the external magnetic field is uniform, this interaction is not present. The last term in Equation (37) represents the self interaction of the external magnetic field in a higher order in the topological mass.
4. Conclusions
By means of a classical nonrelativistic U(1) × U(1) gauge field model for the electromagnetic interaction of electrons, we have shown how to find the mean-field Hamiltonian describing composite fermions in 2 + 1 dimensions. For this purpose, the Dirac Hamiltonian formalism for constrained systems was considered.
Furthermore, in Section 2, we showed how the Coulomb interaction naturally appears while in the usual formulation it is introduced ad hoc. In the usual formulation, Equation (22) is taken as a constraint of the theory. In this paper, we derived its validity from the constraint structure.
Finally, in Section 3, we saw that the inclusion of a topological mass term for the electromagnetic field in the Lagrangian density introduces interaction terms absent in the canonical Hamiltonian (29).
Acknowledgements
The authors acknowledge Dr. R. Id Betan for his invaluable contribution and helpful discussions.
Cite this paper
Edmundo C.Manavella,Carlos E.Repetto, (2015) Alternative Derivation of the Mean-Field Equations for Composite Fermions. Journal of Modern Physics,06,1737-1742. doi: 10.4236/jmp.2015.612175
References
- 1. Jain, J.K. and Anderson, P.W. (2009) Proceedings of the National Academy of Sciences of the United States of America,
106, 9131-9134.
http://dx.doi.org/10.1073/pnas.0902901106 - 2. Lu, H., Das Sarma, S. and Park, K. (2010) Physical Review B, 82, 201303(R).
http://dx.doi.org/10.1103/PhysRevB.82.201303 - 3. Girvin, S.M. and MacDonald, A.H. (1987) Physical Review Letters, 58, 1252-1255.
http://dx.doi.org/10.1103/PhysRevLett.58.1252 - 4. Zhang, S.C., Hansson, T.H. and Kivelson, S.A. (1989) Physical Review Letters, 62, 82-85.
http://dx.doi.org/10.1103/PhysRevLett.62.82 - 5. Jain, J.K. (1989) Physical Review Letters, 63, 199-202.
http://dx.doi.org/10.1103/PhysRevLett.63.199 - 6. Schrieffer, J.R. (1964) Theory of Superconductivity. W.A. Benjamin, Inc., New York.
- 7. Mahan, G.D. (2000) Many-Particle Physics. 3rd Edition, Kluwer Academic/Plenum Publishers, New York.
http://dx.doi.org/10.1007/978-1-4757-5714-9 - 8. Manavella, E.C. (2001) International Journal of Theoretical Physics, 40, 1453-1474.
http://dx.doi.org/10.1023/A:1017505511427 - 9. Manavella, E.C. and Addad, R.R. (2009) International Journal of Theoretical Physics, 48, 2473-2485.
http://dx.doi.org/10.1007/s10773-008-9925-5 - 10. Halperin, B.I., Lee, P.A. and Read, N. (1993) Physical Review B, 47, 7312-7343.
http://dx.doi.org/10.1103/PhysRevB.47.7312 - 11. Lopez, A. and Fradkin, E. (2003) Fermionic Chern-Simons Field Theory for the Fractional Hall Effect. In: Heinonen, O., Ed., Composite Fermions, World Scientific, Singapore.
- 12. Lopez, A. and Fradkin, E. (1991) Physical Review B, 44, 5246-5262.
http://dx.doi.org/10.1103/PhysRevB.44.5246 - 13. Jain, J.K. (2007) Composite Fermions. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511607561 - 14. Greiner, W. and Reinhardt, J. (1996) Field Quantization. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-61485-9 - 15. Jackiw, R. and Templeton, S. (1981) Physical Review D, 23, 2291-2304.
http://dx.doi.org/10.1103/PhysRevD.23.2291

