Journal of Modern Physics
Vol.06 No.10(2015), Article ID:59223,16 pages
10.4236/jmp.2015.610144
A Classical Complete Action for a System of Small-Point Massive Charged Particles in General Relativity
Gonzalo Ares de Parga, Adriana Avalos-Vargas
Departamento de Física, Escuela Superior de Física yMatemáticas, Instituto Politécnico Nacional, U. P. Adolfo López Mateos, Zacatenco, C.P. 07738, Mexico City, Mexico
Email: gadpau@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 March 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
A classical action which describes the motion of a system of small-point massive charged particles including the existence of the electromagnetic and gravitational self-forces, Maxwell equations and Einstein field equations is presented. The action possesses the particularity of being a functional of the variables zi(τi), the trajectory of the i-particle, Aα(x), the electromagnetic 4-potential, and gαβ(x), the metric tensor. It is also considered that the metric tensor gαβ(x) and the potential Aα(x) are not functions of the trajectory of each particle when the variations with respect to the trajectories of the particles are done. That is, the action is complete. The electromagnetic and the gravitational self-forces are analyzed.
Keywords:
General Relativity, Classical Electrodynamics, Self-Action

1. Introduction
Classical Electrodynamics and General Relativity represent two of the most important theories developed during the last century. Although they are apparently formally consistent and closed models, there still exist some unsolved issues like the electromagnetic and gravitational self-forces. Indeed, even if for many authors the Lorentz-Dirac equation [1] represents the best description of the motion of a charged point particle in Special Relativity, different proposals have appeared in order to avoid the unphysical predictions of such equation as the runaway solutions and the preaccelerations [2] . Nowadays, many authors consider the Landau-Lifshitz equation of motion as an excellent approximation which prevents questionable solutions due to its second order equation characteristic [3] -[7] . On the other hand, Yaghyian [8] supports the Lorentz-Dirac equation basically arguing that due to the structure of the charge, the problematic aspects of the equation can be put on a side. The Lorentz- Dirac equation can be generalized to General Relativity by using the Principle of Equivalence but the result fails to coincide with the one obtained by generalizing Dirac’s method to General Relativity [9] [10] . Two new terms appear, one geometrical, Ricci term, and the other depending on the past of the particle, the tail term, making unworkable the principle of equivalence for charged particles. However, some authors still defend the Principle of Equivalence [11] [12] , contributing to enlarging the discussion about the equation of motion of a charged particle in General Relativity [13] . However, different calculations done applying distinct methods lead to the same Hobbs equation. Indeed, López-Bonilla et al. [14] among others, by using Teitelboim-Plebañski average technique [15] [16] , obtained the Hobbs equation. A very formal deduction has been exposed by Poisson, Pound and Vega [17] where different techniques and method are used in order to deduce the equation. The method used Hadamard’s Green solutions [18] and Detweiler technique [19] [17] to define a regular Green solution avoiding the mass renormalization. This formal deduction makes very conceivable the Hobbs equation. Moreover, applying similar arguments for obtaining the Landau-Lifshitz equation, Hobbs equation can be modified in order to get a Landau-Lifshitz like equation in General Relativity where the geometrical and tail terms are recovered [20] .
On the other hand, using a similar method for the electromagnetic case, Mino [21] and Quinn and Wald [20] , among others, obtained an equation which described the gravitational self-force of a non charged particle submitted to a background (vacuum) gravitational field, the MiSaTaQuWa equation. Moreover, a renormalization process can be avoided also by using Detweiler technique [19] , as it has been shown by Poisson et al. [17] . However, a general equation of motion which includes the electromagnetic and gravitational self-forces, for a charged particle interacting with other particles, seems to be very difficult to obtain due to the non-linearity of the equations in General Relativity.
The idea of a small-point charged massive particle may be confusing, since in general a point particle is represented as a delta function and generates divergences. In fact, it behaves as a black hole. Therefore, it is necessary to represent the point particle as an extended body. However, as Wald and Quinn [20] have noticed, an extended body will presumably collapse to a black hole before a point particle limit can be achieved. Then, it has to be considered that the size, the charge and the mass of the particle are sufficiently small compared with the scale of the variation of the electromagnetic and gravitational background fields, and the self-field effects do not become dominant but are not negligible. Finally, although some attempts have been made to propose an internal structure of the electron [22] , a small-point particle will be represented by using a Delta function but with the constraint described above.
The motion of charged particles are described by adding to the Lorentz force, the self-force. The Lorentz force can also be obtained by proposing an action with an external field [23] , but the self-force has to be added too. Moreover, an action for a single charged can also be considered leading to the self-force term deduced by Hobbs [17] . In a similar way, by considering a background gravitational field (vacuum), a gravitational self- force is obtained, the MiSaTaQuWa equation. However, when a general action is considered in order to obtain equations of motions for charged particles, Maxwell equations and Einstein field equations, the action has to be separately treated. Indeed, first the action is varied as functional of the trajectories, where the potentials Aα and the metric tensor gαβ are taken as functions of the trajectories zi of each particles, then for obtaining the Maxwell equations and the Einstein field equations, the potentials Aα and the metric tensor gαβ are considered as functions of the 4-vector coordinate, x, of the 4-volume [24] . Moreover, in this scheme, the electromagnetic and gravi- tational self-forces are hidden. Finally, we can support Hammond’s idea that the deduction of the reaction term is quite artificial. Indeed, citing Hammond [25] : “In other words, it is not assumed a priori that a self-inter- actions exists, it is not put into the action principle from which the equations are derived, it is a consequence of the theory. This result, that self-interactions are not included in the basic formulation of theory, has been called a formal inconsistency in the theory”. The purpose of this article consists of proposing a complete functional action for a system of charged small-point particles which is stationary with respect to small variations of the trajectories, zi, the potentials, Aα(x), and the metric tensor, gαβ(x), leading to the equations of motion for each particle including the self-forces, both electromagnetic and gravitational, Maxwell equations and Einstein field equations. It has to be noticed that the existences of the self-forces are formally obtained but their expressions are not deduced. Is worth noting that the obtained action is original because normally in the particle and interaction actions, the mistake of writing both actions as functions of the particle trajectories is committed.
At first glance, one might think that the system of equations, including the self-forces, makes no sense because the electromagnetic field and the metric tensor diverge at the particle world lines. However, as we have noted above, the different techniques developed to obtain an expression for the self-forces avoid the divergences by using renormalization processes as Dirac [1] did or by considering regular Greens functions as Detweiler did [17] [19] , among others. In both cases, an average of a regular field (not divergent) over a small surface is accomplished in order to calculate the self-force; in this order of ideas the concept of small-point massive charged particle is consistent with the technique cited above. Moreover, as we mentioned before, the use of the point character of the charged particles represents just a ruse due to the unknowledge of the structure of the charges. Moreover, a technique developed by Tessarotto et al. [26] , by using a wire function which can be identified with a suitable distribution of the charge, may avoid the divergences. Or simply, as an axiomatic approach, in order to avoid the divergences, it is convenient to require that the average techniques describe the self-actions on small- point particles.
One might ask why quantum picture is not adopted. Indeed, Galley et al. [27] provides a quantum field theoretical derivation of the Abraham-Lorentz-Dirac equation and of the MiSaTaQuWa equation. Although the approach is performed with an interaction action which contains parallel propagators, 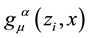 , in the particle action the parallel propagator is not included. Indeed, in an interaction action, the stress-energy tensor ex- pression contains the parallel propagators. For obtaining, the Einstein field equations, Poisson et al. [17] use a particle action with a metric tensor which is function of the trajectory of the particle. They claimed that the energy-stress tensor is derived by functional differentiation of the particle action with respect to metric tensor evaluated at x, that is
, in the particle action the parallel propagator is not included. Indeed, in an interaction action, the stress-energy tensor ex- pression contains the parallel propagators. For obtaining, the Einstein field equations, Poisson et al. [17] use a particle action with a metric tensor which is function of the trajectory of the particle. They claimed that the energy-stress tensor is derived by functional differentiation of the particle action with respect to metric tensor evaluated at x, that is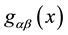 . This is done by expressing
. This is done by expressing . Therefore, the purpose of the article will be accomplished by including the parallel propagators in the complete action. Quantum aspects are not considered since the goal consists of finding the form of the complete action.
. Therefore, the purpose of the article will be accomplished by including the parallel propagators in the complete action. Quantum aspects are not considered since the goal consists of finding the form of the complete action.
Summarizing, the difference with the standard treatments consists of including the parallel propagator in the particle and interaction actions in order to obtain an action for a system of charged small-point particles which functionality does not possesses inconsistencies and the variations of each degree of freedom, 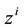 ,
, 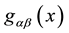 and
and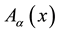 , lead to the equations of motion for each particle, the Einstein field equations and the Maxwell equations in curved space.
, lead to the equations of motion for each particle, the Einstein field equations and the Maxwell equations in curved space.
The article is organized as follows: in the second section, the complete functional action for a system of charged particle in curved space is proposed. The third section is advocated to obtain the formal equations of motion for each particle with self-forces, both electromagnetic and gravitational, the Maxwell equations and the Einstein field equations. In the fourth section, an analysis about the self-forces is presented. Some concluding remarks are done in the fifth section.
2. The Complete Action
2.1. Least Squares Estimation and Strong Consistency
In order to describe the motion of a charged particle submitted to an external electromagnetic field in Special Relativity, a simple action is proposed,
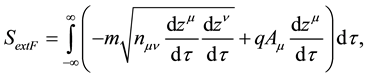 (1)
(1)
where m, 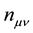 ,
, 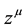 , τ, q and
, τ, q and 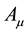 represent the mass of the particle, the Minkowski metric tensor, the 4-vector coordinate of the particle, the proper time of the particle, the charge of the particle and the 4-vector electro- magnetic potential, respectively. By considering that the action is stationary with respect to small variations of the particle trajectory, the Lorentz force is obtained
represent the mass of the particle, the Minkowski metric tensor, the 4-vector coordinate of the particle, the proper time of the particle, the charge of the particle and the 4-vector electro- magnetic potential, respectively. By considering that the action is stationary with respect to small variations of the particle trajectory, the Lorentz force is obtained
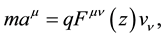 (2)
(2)
where  and
and
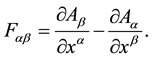 (3)
(3)
Obviously, no reaction force is deduced. The Maxwell equations can be derived by a similar procedure taking an electromagnetic action,
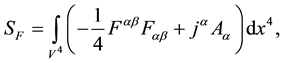 (4)
(4)
and considering that 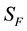 is stationary with respect small variations of the 4-vector potential,
is stationary with respect small variations of the 4-vector potential, 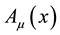 , one obtains
, one obtains

where 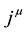
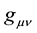
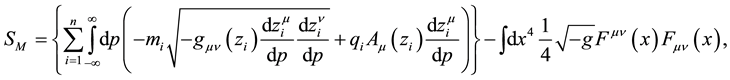
where p, 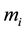
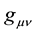
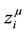
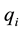
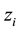
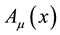
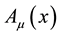
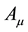
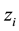
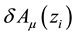
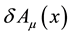

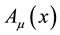
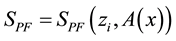
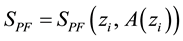
2.2. Parallel Propagator
In order to be able to propose a complete action it is necessary to define some mathematical tools. Let us consider an orthonormal basis, a tetrad 
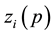
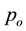
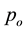
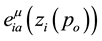
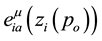
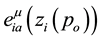
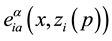
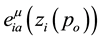
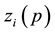

assume that x belongs to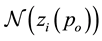
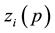
linked to 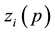


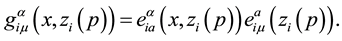
The subscript “i” has been introduced for defining each tetrad for each particle. The uniqueness of 


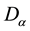
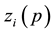
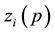
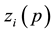
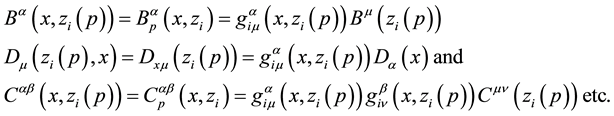
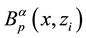
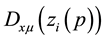


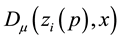

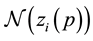
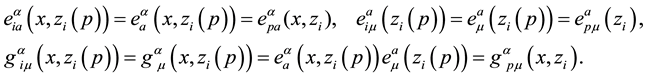
We shall here adopt the convention that indices taken from the letters α to κ in the Greek alphabet are always associated with the point x, while indices taken from λ to ω are always associated with the particle
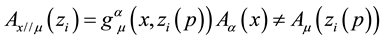
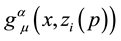
2.3. Complete Action
Once the parallel propagator has been defined , invariant quantities can be introduced in the action. Indeed, the
term 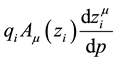
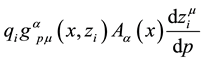
which contains a 4-potential depending on x. A complete action can now be defined. The action will be a functional of the following independent variables: the trajectories of each particles, 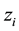
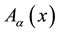

A- The particle action, 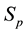
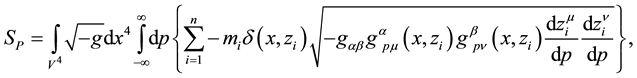
where p represents any parameter and
B- The interaction action, 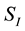
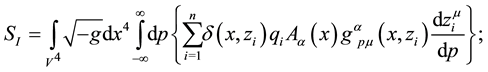
C- The electromagnetic field action, 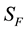
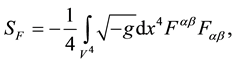
where the electromagnetic field-strength tensor 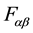
D- The gravitational field action, 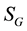
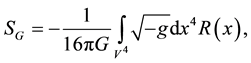
being 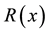

As promised in the introduction, an action is proposed whose independent variables are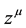
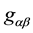
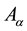

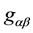
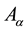
3. The Variation of the Complete Action
Once the action is proposed, the equations arising from them must be derived by making the variations of it with respect to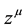
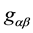
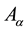
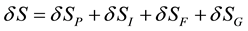


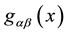

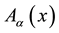
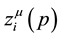

3.1. Variation with Respect to the Metric Tensor δSg
The variation of S with respect to the metric tensor is,

Since
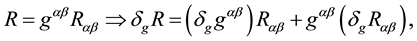
we have
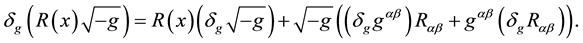
Let us first analyze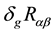
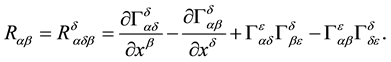
Therefore, it is necessary to notice that the variation of a covariant derivative of a 4-vector is different to the covariant derivative of the variation of a 4-vector; that is: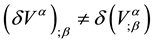
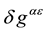
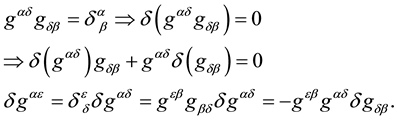
We are now in conditions to calculate the variation of the affine connections,
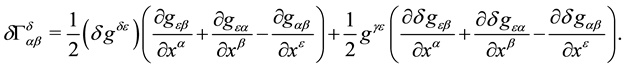
By using Equation (19), we arrive at
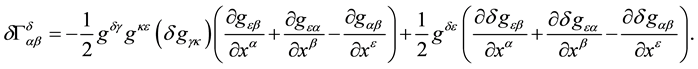
Therefore, from Equations (20) and (21), we obtain that
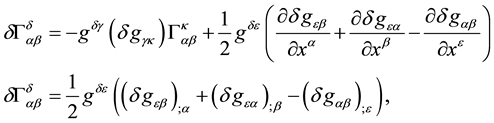
represents a tensor [24] . Therefore, the variation of 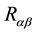
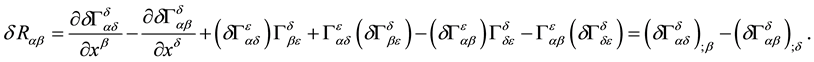
So, the last term of Equation (17) can be written as
On the other hand, since
This term vanishes when it is integrated over the 4-volume. Returning to Equation (17), it is clear that we need to know
By using Equations (19) and (26), the variation of 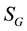
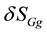

It is clear that if we consider an empty space, it is obtained
field equations in vacuum. However, if the system contains point massive charged particles, the other parts of the action have to be considered. Let us now calculate the variation of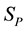

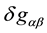
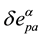
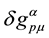
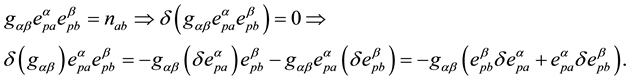
In the other side,
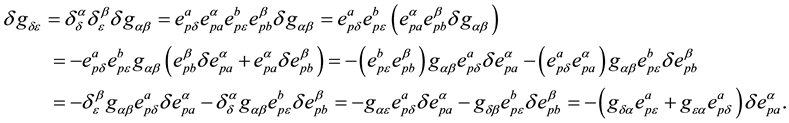
Finally, as an example, the variation of 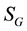
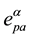
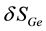
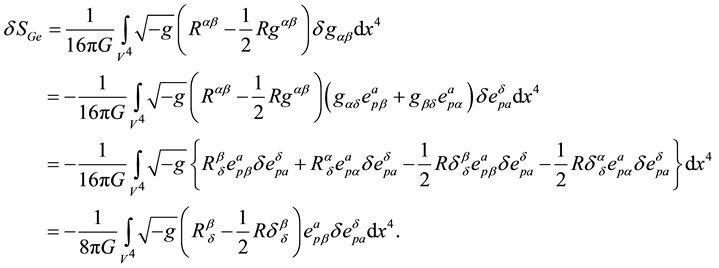
The result described by Equation (27) has been recovered. It has to be remembered that the use of the tetrad is just justified in the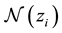
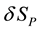

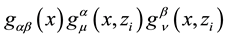

The first variation, 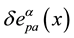
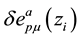

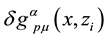
the 4-volume will lead to the same result as considering it as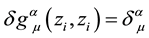
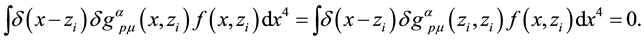
Therefore, we arrive at
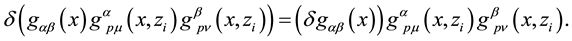
By using Equation (29), we obtain (simplifying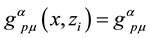
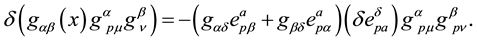
Finally, noticing that 

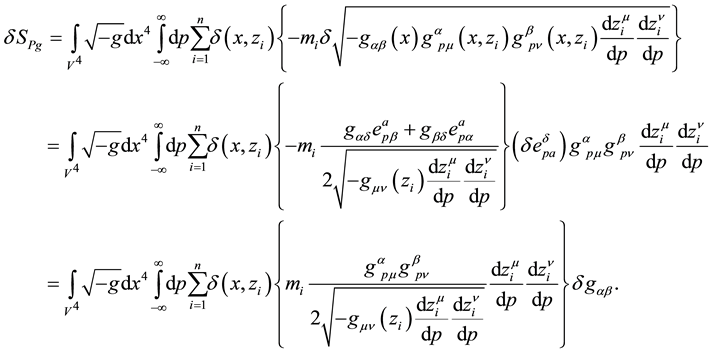
It has to be noticed that we have used the identity, 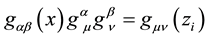
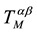
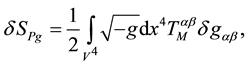
where, by changing the parameter p to the proper time of each particle, 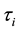
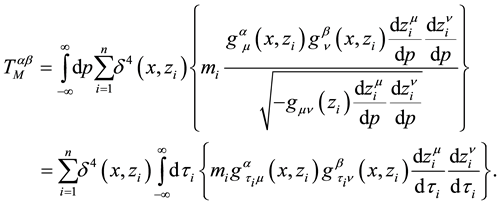
It has to be remarked that, by using Equations (27) and (36), we obtain the Einstein field equations without
charges,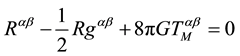
the variation with respect to the tetrads, Equation (30), and substituting Equation (29) in Equation (36). However, in the general case of a system of point massive charged particles, the total energy-momentum tensor, where the effect of the charges is included, has to be considered. That is, the variations of the interaction action, 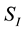

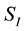

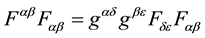
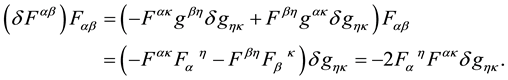
Noticing that the Delta function does not appears in 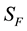
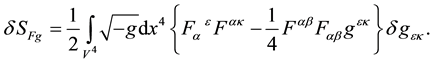
Introducing the electromagnetic energy-momentum, 
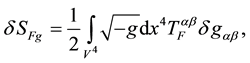
with
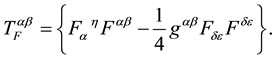
Finally,
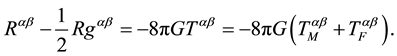
This last expression represents the Einstein field equations for a system of point massive charged particles.
3.2. Variation with Respect to the Trajectories δSz
The variation of the complete action with respect the metric tensor has been achieved. The next step consists on calculating the variation of S with respect to the trajectories of the particles. If we analyze 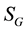
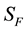
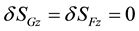
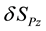
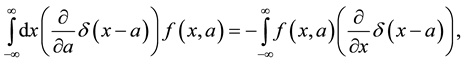
the variation of the Delta function will lead to

where we have not respect the convention (
has to be noticed that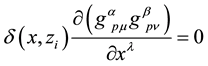
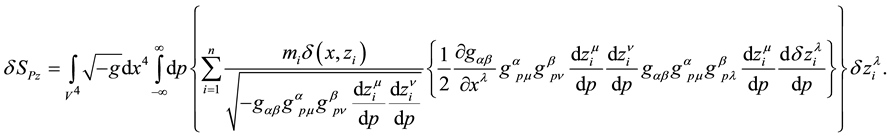
Once we have done the variation, 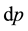
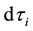
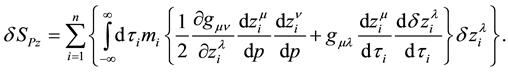
By integrating by parts, we arrive at
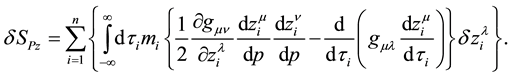
On the other hand,
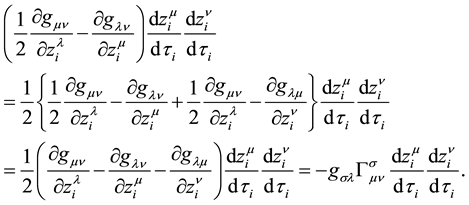
Finally,

where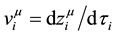
geodesic equation for each particle,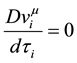
Interaction action has to be taken into account. It has to be remembered that the parallel propagator will not be varied due to similar reasons as in the previous cases.
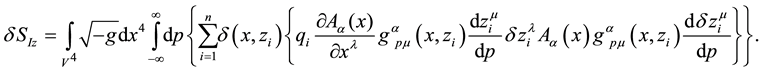
By applying the parallel propagator, integrating over the 4-volume, substituting the parameter p by the proper time of each particle and integrating by parts, we arrive at
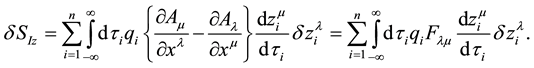
Combining this last result with Equation (49), we obtain
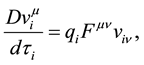
which seems similar to the Lorentz equation in General Relativity. However, when the Maxwell equations in General Relativity will be derived, a rapid inspection will show that the electromagnetic strength tensor in the i-particle, 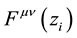
3.3. Variation with Respect to the 4-Potential, δAα(x)
The next step consists of varying with respect the 4-vector potential. Since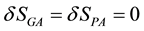
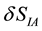
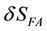
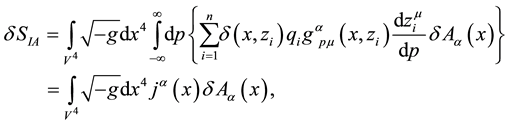
where
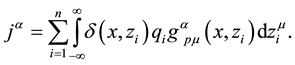
Let us now make the variation of the electromagnetic field action with respect to the 4-potential,
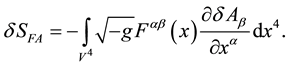
Integrating by parts, we arrive at

Equations (53) and (56) give
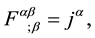
which represent the Maxwell equations in General Relativity. By using Equation (3), we obtain
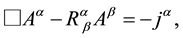
being 
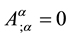
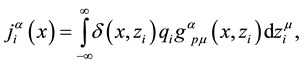
as the current density due to the i-particle. Therefore, each particle generates a 4-potential due to each particle 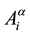
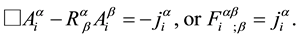
Therefore, we have
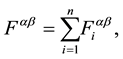
and consequently
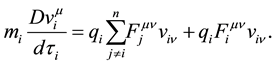
However, 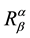
3.4. Summary
From Equations (27), (36), (40), (49), (51), (61), (62), (53) and (56), the variation of the complete action, 
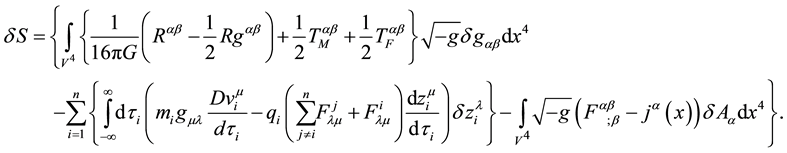
Consequently,
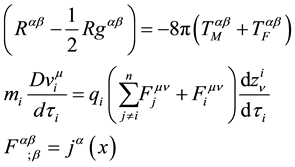
represents a set of coupling equations which describes the metric tensor in all the 4-volume space, the equation of motion for each small-point charged massive particle and the electromagnetic field in all the 4-volume space.
4. Analysis of the Equations
4.1. The Divergences
Equation (64) come from the action, Equation (14) and not from the standard action, Equation (6). It does not represent the standard Einstein-Maxwell system since the electromagnetic self-force for each particle is con-
tained due to the term 
of each particle. However, a simple analysis shows that there exist divergences coming from evaluating the electromagnetic field and the metric tensor at the world line of each particle (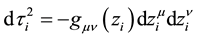
Despite all these arguments, It has been postulated, as a property of the small-point particle, that the self-force can be obtained by an average over a surface of the field following the particle [17] . Even if the average field diverges on the world line, it does not contribute to the net force and just the regular part of the average gives an effective force which can be considered as the self-force in both cases, electromagnetic or gravitational.
4.2. A Single Small-Point Massive Particle in a Background Vacuum Gravitational Field
As we mentioned before, the DeWitt and Brehme equation [9] , corrected by Hobbs [10] , represents the first attempt to obtain an equation of motion for a point massive charged particle in a curved space. However, for our purpose, it is preferable to start by analyzing the case of a the self-gravitational effect in a background vacuum gravitational field which tensor metric is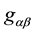
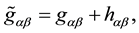
where 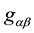
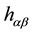
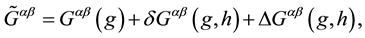
where 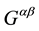
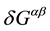
contains the nonlinear terms. A trace-reversed metric perturbation is defined, 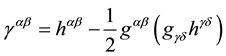
by imposing the Lorentz gauge condition, 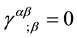
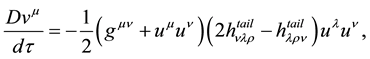
where 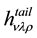
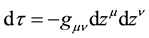
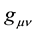
4.3. A System of Small-Point Massive Charged Particles
First of all, it has to be noted that Equation (67) is obtained for a vacuum background gravitational field. When a system of non-charged particles is considered, the situation is more complicated. Indeed, in order to obtain the wave equation, it has been supposed that not only there is no other particles in the point considered but in all the space. That is, the background metric tensor has to be such that the vacuum Einstein equations are satisfied in all
the space; that is: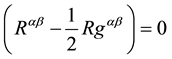
that is such that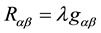
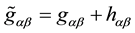

where
In 1960, before the gravitational self-force was proposed, DeWitt and Brehme [9] proposed an equation of motion for a charged particle which contains the electromagnetic self-force in a curved space. A few years later, Hobbs [10] corrected the equation by adding the so-called Ricci term. A very elegant and formal deduction of it can be found in the work done by Poisson et al. [17] . However, if we make an analysis of the Hobbs equation, as for example in Poisson et al. review [17] , we will notice that, apart from the special notion of point charged particle, there is no special consideration on the metric tensor which describes the curved space. That is, the metric tensor corresponds to the one generated by all the particles including the charged particle itself. This means that Equation (62) holds and we just need to substitute the expression of the self-force and the metric tensor has to be considered as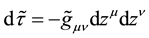
It has to be noted that 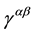
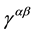
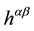

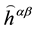
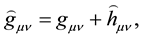
which can be considered as the effective metric tensor at the world line of the particle and the proper time must be expressed as an effective proper time
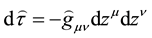
In the case of a single small point massive particle, It has to be also mentioned that the equation of motion is obtained by considering that the proper time represents an affine parameter of the geodesic. However, in the general case, due to the presence of electromagnetic forces the proper time is not anymore an affine parameter and therefore the expression for the acceleration is not so simple. The generalization of the Hobbs equation for a system of small point massive charges, considering the gravitational self-force, may be written as:
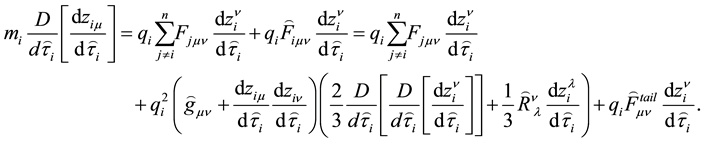
It has to be noticed that even for non-charged particles the calculation of the metric tensor 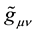
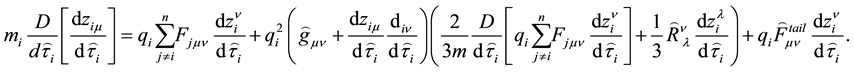
5. Concluding Remarks
There are three lines in order to close the problem: the first one consists of clarifying the doubts about the non- unicity of the self-actions starting by the different equations in Special Relativity [2] ; secondly, it is necessary to justify that the deduction of the self-forces is covariant taking into account the arguments related with illegitimate mathematical operation of summing vectors in different tangent spaces [28] , and with the possible non-generally covariance of the MiSaTaQuWa equation which apparently reflects a specific choice of coordinate system and does not preserve its form under an infinitesimal coordinate transformation [29] ; finally, the calculation of the metric tensor 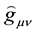
The main result of this article is that it has been shown that from a complete action the Einstein field equations, the Maxwell equations and the equations of motions including the self-actions can be deduced. In these orders of ideas, the formal inconsistency of the theory, commented by Hammond [23] , partially disappears since even if the existences of the self-actions have been derived from an action principle, the deductions of their explicit forms are based on different anzats that generate, as we have mentioned, many discussions about their validities [2] [11] - [13] [28] [29] .
Acknowledgements
This work was partially supported by C.O.F.A.A and E.D.I., I.P.N.
Cite this paper
Gonzalo Aresde Parga,AdrianaAvalos-Vargas, (2015) A Classical Complete Action for a System of Small-Point Massive Charged Particles in General Relativity. Journal of Modern Physics,06,1390-1406. doi: 10.4236/jmp.2015.610144
References
- 1. Dirac, P.M. (1938) Proceedings of the Royal Society of London A, 167, 148-169.
http://dx.doi.org/10.1098/rspa.1938.0124 - 2. Parrot, S. (1987) Relativistic Electrodynamics and Differential Geometry. Springer, New York.
http://dx.doi.org/10.1007/978-1-4612-4684-8 - 3. Spohn, H. (2000) Europhysics Letters, 50, 287-292.
http://dx.doi.org/10.1209/epl/i2000-00268-x - 4. Rohrlich, F. (2000) American Journal of Physics, 68, 1109 -1113.
http://dx.doi.org/10.1119/1.1286430 - 5. Rohrlich, F. (2001) Physics Letters A, 283, 276-278.
http://dx.doi.org/10.1016/S0375-9601(01)00264-X - 6. Rohrlich, F. (2007) Classical Charged Particles. Word Scientific Publishing Co., Danvers.
http://dx.doi.org/10.1142/6220 - 7. Ares de Parga, G. (2006) Foundations of Physics, 36, 1474-1510.
http://dx.doi.org/10.1007/s10701-006-9072-x - 8. Yaghjian, A.D. (1992) Relativistic Dynamics of a Charged Sphere. Springer, New York.
- 9. DeWitt, B.S. and Brehme, R.W. (1960) Annals of Physics, 9, 220-259.
http://dx.doi.org/10.1016/0003-4916(60)90030-0 - 10. Hobbs, J.M. (1968) Annals of Physics, 47, 141-165.
http://dx.doi.org/10.1016/0003-4916(68)90231-5 - 11. Boulware, D. (1980) Annals of Physics, 124, 169-188.
http://dx.doi.org/10.1016/0003-4916(80)90360-7 - 12. Singal, A.K. (1995) General Relativity and Gravitation, 27, 953-967.
http://dx.doi.org/10.1007/BF02113077 - 13. Parrot, S. (2002) Foundations of Physics, 32, 407-440.
http://dx.doi.org/10.1023/A:1014861329235 - 14. López-Bonilla, J.L. Morales, J. and Rosales, M.A. (1994) Pramana: Journal of Physics, 43, 273-278.
http://dx.doi.org/10.1007/BF02846843 - 15. Teitelboim, C. (1971) Physical Review D, 4, 345-347.
http://dx.doi.org/10.1103/PhysRevD.4.345 - 16. Plebañski, J. (1972) The Structure of the Field of a Point Charges. Internal report CINVESTAV-IPN, Mexico.
- 17. Poisson, E., Pound, A. and Vega, I. (2011) Living Reviews in Relativity, 14, 1-190.
http://dx.doi.org/10.12942/lrr-2011-7 - 18. Hadamard, J. (1923) Lectures on Cauchy’s Problem in Linear Partial Differential Equations. Yale University Press, New Haven.
- 19. Detweiler, S. and Whiting, B.F. (2003) Physical Review D, 67, Article ID: 024025.
http://dx.doi.org/10.1103/PhysRevD.67.024025 - 20. Quinn, T.C. and Wald, R.M. (1997) Physical Review D, 56, 3381-3394.
http://dx.doi.org/10.1103/PhysRevD.56.3381 - 21. Mino, Y., Sasaki, M. and Tanaka, T. (1997) Physical Review D, 55, 3457-3476.
http://dx.doi.org/10.1103/PhysRevD.55.3457 - 22. Ghosh, S., Choudhury, A. and Sarma, J.K. (2013) Indian Journal of Physics, 87, 607-611.
http://dx.doi.org/10.1007/s12648-013-0254-z - 23. Landau, L.D. and Lifshitz, E.M. (1962) The Classical Theory of Fields. Pergamon, London.
- 24. Weinberg, S. (1972) Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley & Sons, New York.
- 25. Hammond, R.T. (2010) EJTP, 7, 221-258.
- 26. Tessarotto, M., Dorigo, M., Cremaschinid, C., Nicolinia, P. and Beklemishev, A. (2008) The Exact Radiation-Reaction Equation for a Classical Charged Particle. arXiv:0807.1819v1.
- 27. Galey, C.R., Hu, B.L. and Lin, S.Y. (2006) Physical Review D, 74, Article ID: 024017.
http://dx.doi.org/10.1103/PhysRevD.74.024017 - 28. Parrot, S. (2003) Energy Radiation of Charged Particles in Conformally Flat Spacetimes. arXiv:gr-qc/9308023v3.
- 29. Kim, D.H. (2005) Radiation Reaction in Curved Spacetime. Ph.D. Thesis, University of Florida, Gainesville.
- 30. Geroch, R. and Traschen, J. (1987) Physical Review D, 36, 1017-1031.
http://dx.doi.org/10.1103/PhysRevD.36.1017 - 31. McGregor, M.H. (1992) The Enigmatic Electron. Kluer Academic Publishers, Dordrecht.
- 32. Barut, A.O. and Zanghi, N. (1984) Physical Review Letters, 52, 2009-2012.
http://dx.doi.org/10.1103/PhysRevLett.52.2009 - 33. Ghosh, S., Choudhury, A. and Sarma, J.K. (2012) Apeiron, 19, 247-263.
- 34. Ghosh, S., Choudhury, A. and Sarma, J.K. (2012) Indian Journal of Physics, 86, 481-483.
http://dx.doi.org/10.1007/s12648-012-0083-5 - 35. Barack, L. (2000) Physical Review D, 62, Article ID: 084027.
http://dx.doi.org/10.1103/PhysRevD.62.084027 - 36. Pound, A. and Poisson, E. (2008) Physical Review D, 77, Article ID: 044013.
http://dx.doi.org/10.1103/PhysRevD.77.044013 - 37. Vega, I., Wardell, B. and Diener, P. (2011) Classical and Quantum Gravity, 28, Article ID: 134010.
http://dx.doi.org/10.1088/0264-9381/28/13/134010 - 38. Gal’tsov, D.V. and Spirin, P.A. (2008) Gravitational Radiation Reaction in Non-Vacuum Space-Time. CAPRA Meeting, Orleans, France, 1-21.
- 39. Messaritaki, E. (2003) Radiation Reaction on Moving Particles in General Relativity. Ph.D. Thesis, University of Florida, Gainesville.
- 40. Detweiler, S. (2001) Physical Review Letters, 86, 1931-1934.
http://dx.doi.org/10.1103/PhysRevLett.86.1931


