Journal of Modern Physics
Vol.06 No.06(2015), Article ID:56126,9 pages
10.4236/jmp.2015.66077
Velocity Addition Demonstrated from the Conservation of Linear Momenta, an Alternative Expression
Olivier Serret
ESIM Engineer, Cugnaux, France
Email: o.serret@free.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 March 2015; accepted 5 May 2015; published 6 May 2015
ABSTRACT
Is it possible to demonstrate the velocity addition without using a variable time (as it is done in theory of relativity)? The topic of this paper is to propose and demonstrate an alternative expression based on the conservation of linear momenta. The method proposed here is to start from a physical object (and not from a mathematical point), i.e. from an object with a mass. And the hypothesis is inertial mass to be different from gravitational mass. Then, when impulses are added, we get an expression of the velocity addition itself. When numerical predictions are compared with experimental results, the differences are lower than the measures uncertainty. And these numerical results are much close to those predicts by the theory of relativity, nevertheless with a little difference at high velocities. If this demonstration and this expression were validated, it would allow giving an alternative explanation to some experiments and nature observations as Doppler Effect on light celerity. But first, it would be necessary to get from laboratories more precise experimental results, in order to validate or not this hypothesis of the sum of linear momenta with a Variable Inertial Mass.
Keywords:
Velocity Addition, Variable Time, Variable Inertial Mass, Relativity, Light Celerity, Impulse, Linear Momentum, Kinetic Energy, Fizeau’s Experiment

1. Introduction
“The proof was wrong” about theory of relativity according to a serious astrophysician [1] . He wrote that the first proof, especially those coming from the famous eclipse of 1919, was based in part on data manipulation to get the expected results! Then it was not before the 1970s that new methods finally were able to provide solid experimental evidence.
Today there is no doubt that classical Newtonian rules are invalid with light [2] . And relativity [3] is the predominant theory which can supply alternative explanations about this topic of high velocities. The trouble is that it is necessary to do the hypothesis of a variable time. Why can it be a trouble? Because from a century, the variation of time has never been directly measured (the variation of time is only an “explanation” given to some nature observations).
This article follows the previous one: “How to demonstrate Lorentz factor? Variable time vs. variable inertial mass” [4] . It was based on the hypotheses hereafter:
・ Time is universal (there is not a variable time).
・ Length is constant (there is not a contraction with motion).
・ Gravitational mass is constant (as it can be in Newtonian mechanics).
・ Inertial mass is variable (as it can be in theory of relativity).
Now, the idea is to take an object with a mass (and not a mathematical point, as it can be done in Newtonian mechanics and in theory of relativity). Then we have to choose from which physical principle to start. A first attempt was done adding the kinetic energies [5] ; whatever results were extremely closed to those predicts by theory of relativity, the transfer function T was opened to criticism. So we will start here adding the linear momenta (or impulses). Then a comparison with theory of relativity prediction will be interesting: if both results are very close, it remains a little difference which allows distinguishing them.
A velocity addition rule demonstrated without using a variable time would allow an alternative explanation to some nature observations as the Doppler Effect on light celerity, and a universal time would give coherence between the time of the traditional mechanics and the time of the quantum mechanics.
2. Formulas of Velocity Addition
2.1. The Instantaneous Velocity
What is (instantaneous) velocity?
Current definition of velocity is a kinematic definition, based on the description of the movement of a body [6] : it is its displacement 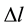 during a time interval
during a time interval , described by the formula:
, described by the formula:
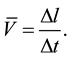 (1)
(1)
Because this definition is based on a time interval, it is in fact the definition of an “average” velocity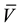 , not of an instantaneous velocity.
, not of an instantaneous velocity.
For the velocity itself, which is an “instantaneous” velocity, it is not so easy to define it, because it is not possible to divide previous formula when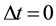 . Let us call
. Let us call 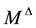 the position of the body M at
the position of the body M at  time. We can see on the Figure 1 hereafter than when
time. We can see on the Figure 1 hereafter than when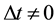 , the physical straight line
, the physical straight line 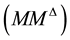 is in the usual case different of the mathematical tangent line
is in the usual case different of the mathematical tangent line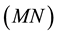 .
.
Figure 1. Instantaneous velocity and tangent.
On a mathematical point of view, it is demonstrated than the director coefficient of the tangent is
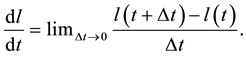 (2)
(2)
And what we call the “instantaneous” velocity V is the “mathematical limit”:
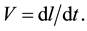 (3)
(3)
Then we have to keep in mind than (instantaneous) velocity is not a physical measure, it is only a mathematical limit.
There is an exception: when the average velocity is constant, the (instantaneous) velocity equals exactly the average velocity.
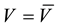 (4)
(4)
It is this case we will consider hereafter, and especially in Galilean reference frames.
2.2. Galilean Reference Frames
A Galilean reference frame, or inertial frame, is a frame of reference that describes time and space homogeneously, isotropically and in a time-independent manner [7] , which is the case of present hypothesis. All inertial frames are in a state of constant, rectilinear motion with respect to one another.
Let us have:
W the velocity of B in the reference frame A, and
w the velocity of A in the reference frame B.
Then by symmetry, we can write
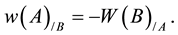 (5)
(5)
Note: To distinguish the two references frames, velocities in one reference frame will be written with capital letters (W for example), and in the second reference frame with small letters (w for example).
2.3. Velocity Addition in Newtonian Mechanics
Let us have the velocity of the object  in the inertial frame B:
in the inertial frame B:
What is the value of the velocity of 

Let us say B is for example a train, and A the ground.
The velocity of the train B seen from the ground A is 

These velocities have been illustrated by Figure 2 and Figure 3.
In Newtonian theory, the velocity of the ball seen from the ground A will be:

In mathematics, vectors are added in the same reference frame. We can note it is not the case for velocities in physics; we could add velocity 

Figure 2. Velocities seen from reference frame A.
Figure 3. Velocities seen from reference frame B.
frame, which could be estimated quite surprising for velocities because a velocity depends of its reference frame. This comment was necessary to get a better approach of the velocity addition through linear momenta in the next paragraphs.
2.4. Velocity Addition in Fizeau’s Experiment
In 1851, to try to prove the existence of aether, Fizeau did an experiment with light at v velocity in water at W motion. He found the velocity addition rule [1] :

with

C being velocity of light in the air.
He wrote the equation this way to distinguish the influence of each reference frame:

but because the term of 
And developing the term of

The expression is not so simple.
2.5. Velocity Addition with Theory of Relativity
In 1905, Einstein demonstrated the velocity addition law:

3. An Alternative Demonstration of the Velocity Addition
3.1. The Hypothesis
Here we propose to use the sum of two impulses (or collinear momenta) on a material body. From the point of view of A, if the mass of the red ball of Figure 2 was initially motionless in B inertial frame, its linear momentum would be



It is the basic hypothesis of the demonstration hereafter. This basic hypothesis can be argued by Noether’s theorem [8] about symmetry: the conservation of linear momenta is a consequence of space invariance. Another argument about this basic hypothesis is given in Appendix I.
3.2. Demonstration
To simplify the writing and the reading, we will not use any longer in the equations hereafter the references to the frames 



Dividing by

This gives:

so

or

Another way to write previous formula (see Appendix II) is:

Remark: at first sight the present law of addition can look a bit complicated. But recall the addition law for velocities in theory of relativity 

they are not so simple either!
4. Comparisons
Let us compare this Equation (17), or (18), with the usual equations and with experimental results.
4.1. Comparison with Newtonian Mechanics
Newtonian velocity addition is invalid with high velocities because the sum could exceed the light celerity.
It is not the case with the formula of this paper which cannot give results higher than 

4.2. Comparison with Theory of Relativity
We have built this chart to compare present VIM predictions (VIM for variable inertial mass) to SRT predictions (SRT for Special Relativity Theory), with a typical speed of an electron in a cathode ray tube 
VIM addition predictions are a bit lower than SRT addition predictions. But in practice, the numerical results are so much close and the differences are of the same order than the experiment precision.
4.3. Comparison with Fizeau Experimental Results
Then we have compared the prediction of this velocity addition with experimental measures, which is the true way to validate or not a theory.
In 2011, using an inexpensive setup, an undergraduate laboratory in Toulouse, France, measured again Fizeau’s experiment with such results: “We observe that the experimental points almost systematically lie above the relativistic value” [9] , it is written on page 6 by this laboratory. The relativistic slope without correction is 9% lower than the experimental slope! That means than the same experiment done in an undergraduate laboratory in 2011 with modern means would be significantly less precise than in 1886 [10] ! This could also mean that the old measures would have been corrected a bit to better match with the expected curve.
The difficulty in 2011 experiment was to measure precisely the local velocity of water along the center of the pipes because of flow turbulence and because of the corners. And to be more concrete, if experimental data were converted from “difference of radian” to “difference of light velocity”, the measures on light velocity (with an average constant velocity of water of 5 m/s) would be from 3 to 4 m/s where Newtonian mechanics predicts 10 m/s, SRT (Special Relativity Theory) predicts 4 m/s and present VIM (variable inertial mass) hypothesis predicts 3 m/s. So more accurate and stable experimental conditions (especially on water motion) and more precise measures would be necessary.
5. Conclusions
First step was to replace the variable time by a variable inertial mass (see “How to demonstrate the Lorentz factor” [4] ). Then in present article, the question was to know if it was possible to apply the variable inertial mass in other applications like the velocity addition.
The Newtonian mechanics and the theory of relativity both consider velocity applied to a mathematical point, i.e. to an object without mass. In this paper it has been considered a physical object with a mass, and the originality is to do the hypothesis that inertial mass is different of gravitational mass. Starting with the conservation of linear momenta (Newton 3rd law), and using the Lorentz factor, we find a new velocity addition rule: the total velocity U is such as
This expression can look a bit complicated but the results are close from theory of relativity predictions and about all these theoretical results appear to be very close to experimental measures.
If 2011 results of Fizeau’s experiment were confirmed, it would mean that present addition rule described the
Table 1. Comparison of results.
reality in an equivalent way, and maybe a better way than theory of relativity could do it! So Neo-Newtonian theory with a variable inertial mass would be considered as a valuable alternative to the variable time hypothesis. In this case, it would give coherence between the time of the traditional mechanics and the time of the quantum mechanics. It would also change our understanding of light celerity in Doppler Effect, astrophysical movements and other physical points where light celerity is engaged. For example, next demonstration should be about gravitational deflection of light.
Acknowledgments
I would like to thank Prof. B. Blaive, Prof. R. Boudet and Dr. Z. Oziewicz for their encouragement and their links, and Dr. C. Whitney for relevant remarks about first velocity addition based on kinetic energy. I thank also R. Mathevet and his colleague for showing me the Fizeau set up and for having supplied the raw data of their experiment.
References
- Bonnet-Bidaud, J.-M. (2008) Astrophysician at CEA (Commissariat à l’Energie Atomique). Les preuves étaient faus- ses. http://www.cieletespace.fr/evenement/relativit-les-preuves-taient-fausses
- Wikipedia, History of Special Relativity. http://en.wikipedia.org/wiki/History_of_special_relativity
- Einstein, A. (1979) La relativité, from Édition Payot.
- Serret, O. (2015) Journal of Modern Physics, 6, 252-259. http://dx.doi.org/10.4236/jmp.2015.63030
- Serret, O. (2012) Mass of Inertia and Kinetic Energy. http://gsjournal.net/Science-Journals/Research%20Papers-Relativity%20Theory/Download/4113
- Serres, M. and Farouki, N. (1997) Le Trésor-Dictionnaire des Sciences. Ed. Flammarion, 1037.
- Landau, L.D. and Lifshitz, E.M. (1960) Mechanics. Pergamon Press, Oxford, 4-6.
- Noether’s Theorem. http://en.wikipedia.org/wiki/Noether%27s_theorem
- Lahaye, T., Labastie, P. and Mathevet, R. (2012) Fizeau’s “Aether-Drag” Experiment in the Undergraduate Laboratory. http://arxiv.org/abs/1201.0501
- Fizeau, H. Hypothèses relatives à l’éther lumineux. http://www.orgonelab.org/EtherDrift/Fizeau1851.pdf
Appendix I
A justification about the Equation (12): 
Let us have 2 reference frames and 3 bodies:
First reference frame is a Galilean one, called A.
Second one is a Galilean reference frame, called B.
W is the velocity of B in A reference frame (see Figure A1).
The first body is a huge one (the Earth for example), with a gravitational mass M.
The second is a large one (a train for example), with a gravitational mass N.
The third is a small one (a red ball for example), with a gravitational mass m.
and remind the difference between two definitions:
Linear momentum:

Impulse:

The linear momentum of two bodies is the sum of each linear momentum within the same reference frame, whatever the velocity v would be:



Let us remind the consequence of Newton’s Third Law about linear momentum: when no other forces act on the bodies, then the total linear momentum of the bodies remain unchanged. So, if we did not get any linear momentum previously, when a first impulse has been given from M to the two bodies N and m, it means an opposite impulse has been given to the base M (see Figure A1):

And according to Equation (A5)
with 




Figure A1. Velocities seen from A after the first impulse.
Now, let us give from N a second impulse to m, in order that N has no motion in the A reference frame. What is now the situation in the A reference frame? N is motionless by construction, there is no change on M which keeps its velocity



The velocity of the B reference frame in A is W, and by symmetry the velocity of A in the B reference frame is

N is motionless in A reference frame, so after the second impulse N get the same motion than A.
So the velocity of N in the B reference frame is the velocity of A, i.e. 

So

The second impulse has been given from N to m (whatever the motion of M); by conservation of the linear momentum:

with

To summarize the situations, please check Table A1:
Let us sum previous Equations (A7) and (A17):


But

So
Figure A2. Velocities seen from B after the second impulse.
Table A1. Velocities in the two reference frames.


and with Equation (A11)

i.e. for the mass m:

Appendix II
Equivalence between Equation (18) and Equation (17):
Equation (18) is:


means

so


then










