Received 26 February 2015; accepted 13 March 2015; published 17 March 2015

ABSTRACT

The actual value of Higgs boson mass is difficult to determine theoretically due to lack of knowledge on the exact value of Higgs self coupling constant l. The purpose of this paper is to obtain an upper bound on the Higgs mass in the Standard Model on the basis of one-loop effective potential in the ’t Hooft-Landau gauge and MS scheme. The condition of positivity of mass matrix at ϕ = ϕ₀ (where ϕ₀ is the absolute minimum of the effective potential) of the scalar field gives an upper bound on the Higgs self coupling as l ≤ 0.881. This condition yields an upper bound on the Higgs mass as m_H ≤ 229.48 GeV.

Keywords:

One-Loop Effective Potential, Standard Model, Mass Matrix, Higgs Boson Mass

1. Introduction

The Standard Model (SM) [1] is a full relativistic quantum field theory and it combines the electro-weak and strong interactions based on the local SU(3)_C × SU(2)_L × U(1)_Y gauge group. The Higgs mechanism has been introduced in order to give masses to fermions and gauge bosons without violating gauge principles. The introduction of a weak isodoublet of scalar fields gives rise to a physical particle, the Higgs boson. The self-interac- tion of the scalar field leads to a non-zero field strength in the ground state. Through the interaction with the non-zero Higgs field in the ground state, the electro-weak gauge bosons and the fundamental matter particles acquire their masses. The Higgs boson gives the mechanism by which the particles can acquire mass. To confirm these ideas more rigorously it is important to find first hand evidence for the Higgs field. We still have only vague ideas and speculations about the properties of Higgs, which is a hypothetical particle, and the search for Higgs boson is one of the main goals of present and future high energy colliders. On the one hand, the experimental verification of the Standard Model cannot be considered complete until the structure of the Higgs sector is not established by experiment. On the other hand, the Higgs is directly related to most of the major open problems of particle physics, like the flavour problem or the hierarchy problem, the latter strongly suggesting the need for new physics near the weak scale, which can also clarify the dark matter identity. The detection of the Higgs particle [2] is extremely important for the understanding of the fundamental interactions among the quarks and leptons, as well as the generation of masses of fundamental particles given by spontaneous symmetry breaking. In the Standard Model the properties of the Higgs particle are uniquely determined, once its mass is fixed. Unfortunately, the Higgs boson mass is a free parameter of the theory. The Higgs boson has been searched at LEP 2, and its mass should be greater than 114 GeV. On 4 July 2012, the ATLAS and CMS experiments at CERN’s LHC announced that they had each observed a new particle in the mass region around 125 to 126 GeV. This particle is consistent with the Higgs boson, but it will take further work to determine whether or not it is the Higgs boson predicted by the Standard Model. So, there is still a scope for a renewed interest in the evaluation of Higgs mass until the Standard Model Higgs is confirmed in the LHC experiment.

The Standard Model Higgs is trusted to be an effective theory, only valid up to a cut off energy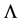. Upper and lower bounds on the Higgs mass have been calculated through the analysis of the scalar effective potential, as a function of the physical cutoff. The upper bound on the Higgs mass is obtained from the triviality bound of the Higgs self coupling constant l and the lower bound from the requirement that the Electro-Weak vacuum should be stable. Here the endeavor is to calculate an upper bound on the Higgs self coupling constant l as well as the Higgs boson mass from the requirement that the eigenvalues of the mass matrix in the shifted Lagrangian density should be positive at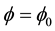, where is the absolute minimum of the effective potential (EP) [3] .

The paper is organized as follows. The theory is given in Section 2. The results and discussions are given in Section 3. The conclusions are given in Section 4.

2. Theory

The one-loop effective potential of the Standard Model in the ’t Hooft-Landau gauge and the MS scheme is [4]

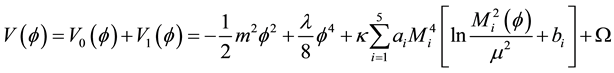(1)

where is the tree level potential and is the one-loop correction, namely

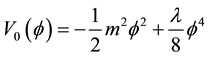
where and the appropriate parameters are [4]

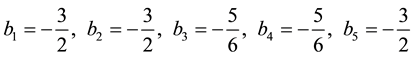
Here is the one-loop contribution to the cosmological constant which will turn out to be irrelevant in our calculation and are the tree-level expressions for the squard eigenmasses of the particles that enter in the one-loop radiative corrections.

For the EP of the minimal SM, the squared eigenmasses are

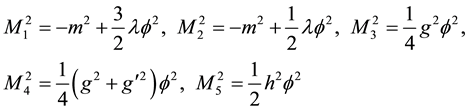
(1 º Higgs, 2 º Goldstone, 3 º W, 4 º Z and 5 º Top).

Where m is the mass parameter and 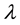is the quartic coupling whereas g, , h are the SU (2), U (1) and top Yukawa couplings respectively.

Using the technique of ref. [3] , we obtain an upper bound on Higgs mass by imposing the condition that all the eigenvalues of the mass-matrix (eigenmasses) be real at the physical point where is the vacuum expectation value of the Higgs field.

So, the conditions (i = 1, 2, 3, 4, 5) are satisfied for all i when

(2)

This is the exact necessary condition that must be satisfied so that all eigenmasses are real at the physical point [3] . It ensures that the effective potential is real at its absolute minimum. This condition demands to be an essential characteristic of the effective potential if its absolute minimum characterizes the vacuum state of the theory.

The effective potential as given in Equation (1) satisfies the condition

This leads to the following equation

(3)

We introduce a function p such that

(4)

and using this function p Equation (3) becomes

(5)

The reality condition (2) suggests that.

Thus the limiting value of the region in which condition (2) is satisfied demands

(6)

where we have taken due to extensive data taken at the resonance.

The limiting value of Higgs coupling is obtained from the condition (6) for the region in which the exact necessary reality condition (2) is satisfied. The Higgs boson mass is given by

Using Equations (1) and (3) we get the expression of Higgs mass for p = 1 as

(7)

3. Results and Discussions

Choosing the following numerical values [5] at viz.

, , , ,

We obtain for m_t = top quark mass = 175 GeV [6] .

In the neighborhood of the variation of shows that for which violates the reality condition (2). Obviously we demand that, is the upper bound on Higgs self coupling constant. Since in practical terms the couplings have to be at most of the order of one in order for the theory to remain perturbative, this value of lies within the perturbative limit of the scalar self-coupling i.e. [7] . Beyond perturbation theory, we still donot know any mechanism that would provide for small masses of the scalar particles.

Using Equation (7) yields. So, for the upper bound of Higgs self coupling, i.e., the corresponding upper bound on Higgs mass comes out to be 229.48 GeV, i.e.

Now, in the study of renormalization group evolution of the Higgs self coupling in the standard model [8] , the one-loop equation for l becomes non linear and is of the Riccati type, whose numerical and analytical solution by incorporating the fact that l must be positive and finite giving the bounds on l as for the validity of Standard Model in the whole range [,(=10¹⁴ GeV)]. Interestingly, this higher bound on l is approximately of the order of the higher bound on l calculated in this paper. The bounds on Higgs mass as calculated in [6] [9] also lies within the upper bound on Higgs mass as comes out in this paper. However, the upper limit based from the indirect precision electroweak data [10] is at 95% C. L. Moreover, on the basis of the supersymmetric extension of the standard model plus one extra dimension Bhattacharyya, Majee and Raychaudhuri [11] found the upper bound of Higgs mass as. Thus the above results of different authors match well with the upper bound on Higgs mass predicted in this paper.

4. Conclusions

On the basis of the above studies, I come to the following conclusions:

1) The upper bound of Higgs self coupling constant is, and the corresponding upper bound on Higgs mass becomes.

2) This bound on Higgs self coupling constant lies within the perturbative limit of the scalar self coupling constant. So, the calculation of upper bounds on Higgs mass and the parameters chosen in this work satisfy the perturbative validity.

3) As far as the selection of appropriate range of energy for the purpose of detection of Higgs mass is concerned, this result will help the LHC experimentalists.

This study suggests that there is still a scope for a renewed interest in the evaluation of Higgs mass until the Higgs is discovered in the LHC experiment.

Cite this paper

Partha PratimPal， (2015) An Upper Bound on the Higgs Self-Coupling and Higgs Boson Mass from the Positivity Condition of the Mass Matrix。 Journal of Modern Physics，06，369-373. doi: 10.4236/jmp.2015.64039

References