Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52082,3 pages
10.4236/jmp.2014.518195
Quantum Effects from a Simple Card Game
Allen D. Allen
Physics Division, New Terra Enterprises, Los Angles, USA
Email: allend.allen@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2014; revised 5 November 2014; accepted 1 December 2014
ABSTRACT
A well-known, classical conundrum, which is related to conditional probability, has heretofore only been used for games and puzzles. It is shown here, both empirically and formally, that the counterintuitive phenomenon in question has consequences that are far more profound, especially for physics. A simple card game the reader can play at home demonstrates the counterintuitive phenomenon, and shows how it gives rise to hidden variables. These variables are “hidden” in the sense that they belong to the past and no longer exist. A formal proof shows that the results are due to the duration of what can be thought of as a gambler’s bet, without loss of generalization. The bet is over when it is won or lost, analogous to the collapse of a wave function. In the meantime, new and empowering information does not change the original probabilities. A related thought experiment involving a pregnant woman demonstrates that macroscopic systems do not always have states that are completely intrinsic. Rather, the state of a macroscopic system may depend upon how the experiment is set up and how the system is measured even though no wave functions are involved. This obviously mitigates the chasm between the quantum mechanical and the classical.
Keywords:
Quantum Mechanics, Hidden Variables, Three Prisoners Problem, Bertrand’s Box Paradox, Monty Hall Problem

1. Introduction
The three prisoners problem [1] [2] , and Bertrand’s box paradox [3] [4] , are well-known, classical conundrums related to conditional probability. They are based upon a counterintuitive phenomenon that also underlies the Monty Hall problem [5] [6] , so called because it has been used for television games. As an example of the Monty Hall problem, a contestant on a television show is given three doors to choose from. Behind one of the doors is a bag full of money. Behind the other two doors is something silly that has no value. The contestant picks one of the doors. Since there is only one chance in three that the contestant will pick the door with the money, contestants will fail to win the money 66.67% of the time on the first try. Next, the contestant is shown what is behind one of the two doors that he did not pick and that is not hiding the money. The contestant is then faced with just two doors, one of which has the money. Even though what is hidden behind the doors is not placed there randomly, there should now be one chance in two, or a 50% probability, that the contestant can pick the door with the money. Nonetheless, the contestant is given an opportunity to change his mind and pick the other door that is still closed. Since classically each of the two doors has an equal chance of having the money hidden behind it, educated contestants usually do not change their selection since the probability of success is the same for each of the two doors: one chance in two. Empirically, however, the contestant has double the chance of winning if he changes his selection.
This is an example of the brain teasers that are based on the phenomenon in question. What has been overlooked in the past is the profound significance of the underlying phenomenon, both in general and especially for physics. In particular, once the contestant has made his initial choice, the probability P for the success of that choice, and therefore the probability 1 ? P for the other choices, remain invariant until the winning door has been revealed, equivalent to the collapse of a wave function, regardless of how much new information is revealed in the meantime.
In the next section, a simple, ad hoc card game illustrates the counterintuitive phenomenon in question, and shows how it creates hidden variables. These variables are “hidden” in the sense that they belong to the past and no longer exist. A lemma in Section 3 demonstrates that this arises from the duration of what may be thought of as a gambler’s bet, without loss of generalization. The bet ends when it is won or lost, analogous to the collapse of a wave function. Until the bet ends, new information that is empowering does not change the original probabilities.
Finally, a related thought experiment in Section 4 shows that, due to this phenomenon, macroscopic objects, such as human beings, do not always have properties that are completely intrinsic. Rather, the state of a macroscopic system may depend upon how an experiment is set up and how the system is measured even in the absence of wave functions.
2. The Card Game
To play the card game introduced in this paper you will need a deck of ordinary playing cards and an assistant to serve as the dealer. Then proceed as follows:
1) The dealer selects three cards from the deck one of which is an ace. It does not matter what the other two cards are so long as there is only one ace.
2) The dealer shuffles the three cards and deals them face down on a table such that you have no idea of which card is the ace.
3) Now you need to pick a card, any one of the three. You indicate your choice by tapping that card.
4) The dealer peeks at the other two cards (the ones you did not tap) and takes away one of those card that is not the ace, returning it to the deck or, better yet, destroying it so the card is physically gone. Note that there will always be at least one such card for the dealer to take away. If the card you tapped happens to be the ace, then there will be two such cards; that is, two cards you did not tap and that are not the ace. If the card you tapped is not the ace, then the ace is one of the two cards you did not tap and there will be only one card the dealer can take away.
This game is not over until at least one of the two cards face down on the table has been turned over revealing which card is the ace. However, let us pause here and consider the situation at this point in time. There are now two cards face down on the table one of which is the ace. Classically, you would expect each of those two cards to have one chance in two of being the ace, a probability of 50%. In truth, however, the card you tapped has only one chance in three of being the ace, a probability of approximately 33%. The other card has double that chance of being the ace: two chances in three or a probability of approximately 67%. It is as if your tap had some strange power to alter future probabilities. If you actually play the game several times, you will see for yourself that these unexpected, asymmetrical probabilities are empirically true as shown by the empirical relative frequencies.
Suppose a third party now comes along and sees the two cards face down on the table. You tell him that exactly one of those two cards is an ace but he does not know anything else about it. He will naturally conclude that there is a 50% chance of picking the ace at random. This is an example of hidden variables. One hidden variable is the card that the dealer took away. Even if that card has been destroyed, it is not really gone until the ace has been revealed and the game is over. The other variable hidden in time is the fact that you tapped a card. This event is not really gone until the ace has been revealed and the game is over. As indicated by the lemma in the next section, these non-classical results are due to the duration of what may be thought of as a gambler’s bet, without loss of generalization. This is analogous to the collapse of a wave function. Indeed, the related thought experiment in Section 4 demonstrates that macroscopic objects do not always have a completely intrinsic state.
3. Formal Proof
Let U be a finite, non-empty set containing n > 2 elements such that $! a Î U, where the unique element a in U may be thought of as the desired object or outcome in U.
Definition 1. A bet β Î U is a unique, fixed element of U arbitrarily selected without replacement, such that the probability β = a is
 (1)
(1)
Lemma: Once created, the bet β Î U exists only so long as β might or might not be the unique element a Î U, such that the probability β = a is neither zero nor one.
Proof: Since n is the cardinality of a finite, non-empty set, it follows that n is a positive integer such that n ≠ 0. Hence, n-1 is a rational fraction. By the exponent of n-1 it follows that n-1 is a rational fraction with numerator 1, such that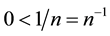 . It follows from the hypothesis that n > 2 that n-1 is a rational fraction with a denominator greater than one, such that
. It follows from the hypothesis that n > 2 that n-1 is a rational fraction with a denominator greater than one, such that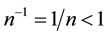 . Since
. Since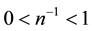 , lemma follows directly from (1) in Definition 1.
, lemma follows directly from (1) in Definition 1.
Definition 2: Given an existent bet β Î U, the unordered pair of distinct elements 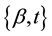 properly contained in U is defined by a process called a reveal, which demonstrates that the probability a is in
properly contained in U is defined by a process called a reveal, which demonstrates that the probability a is in  is zero,
is zero,
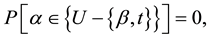 (2)
(2)
equivalently,
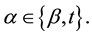 (3)
(3)
Theorem: Given an existent bet β Î U and a reveal demonstrating that a is in the pair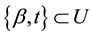 , the probability that a = t is
, the probability that a = t is
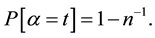 (4)
(4)
Proof: It follows from the hypothesis that 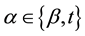 that a is in
that a is in 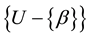 iff a = t. Hence the hypothesis that a = t is logically equivalent to the hypothesis that a is in
iff a = t. Hence the hypothesis that a = t is logically equivalent to the hypothesis that a is in . Likewise,
. Likewise, 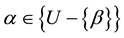 iff a ≠ β. Hence, by the transitive property of logical equivalence, the hypothesis that a = t is logically equivalent to the condition a ≠ β. It then follows directly from (1) in Definition 1 that the probability a = t is 1 ? n-1.
iff a ≠ β. Hence, by the transitive property of logical equivalence, the hypothesis that a = t is logically equivalent to the condition a ≠ β. It then follows directly from (1) in Definition 1 that the probability a = t is 1 ? n-1.
4. Thought Experiment
The author [7] has applied the above theorem to several thought experiments related to love and marriage, office politics, investing, and other problems in order to illustrate that the theorem has utility for everyday life. For the present purposes, however, just one of those examples will suffice.
Consider a single, sexually active, young woman whom we will call Mary. Mary has three boyfriends, Tom, Dick, and Harry. When Mary finds out that she is pregnant, she wants to marry the father of her baby without delay. But she has no way of knowing which of her boyfriends is the father because she has had unprotected sex with all three of them. (The set of three boyfriends is the set U and the father of her baby is the unique element a ÎU.) For an arbitrary emotional reason, she gets engaged to Tom. (This is the bet β Î U). Subsequently, Mary finds out that Dick is infertile. [This is the reveal; we now know that the baby’s father is in the pair {Tom, Harry}.] According to (1) and theorem, respectively, the probability that Tom is the baby’s father is now only one third while the probability that Harry is the father is two thirds.
According to our classical concept of causality, as soon as Mary became pregnant her fetus was the progeny of one particular man. How, then, does the probability that Harry is the father double? This is not because of any biologic information that was revealed. It is because Mary bet on Tom. If she had bet on Harry, then Tom would have had the greater chance of being the father. A sensible way of interpreting this is to use empirical relative frequency. If we arbitrarily select one element β out of n > 2 elements in U as a bet that β = a, then the probability that we guessed wrong and the desired element a is in 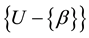 is
is
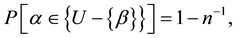 (5)
(5)
which is large for large n. Thus, given many women in Mary’s situation, most will guess wrong if they choose an arbitrary man as the father. In that sense, (5) is not so much about the fetus or the father as it is about the behavior of Mary. Yet, there is no denying that in some sense Mary “caused” the probability that Harry is the father to double by betting on Tom. Recall that if Mary had bet on Harry, then the probability that Tom is the father would have doubled. This is obviously reminiscent of quantum mechanical measurement even though no wave functions are involved. As shown in [7] , none of the above applies if more than one person bets on who the father is and different bets are made. This is a macroscopic example of how decoherence washes out quantum mechanical effects.
5. Conclusion
We have considered a classic conundrum related to conditional probability that has heretofore only been used for games and puzzles. We have seen that the phenomenon in question is more profound, both in general and especially for physics. When illustrated by a simple card game, these counter-intuitive results illustrate variables that are “hidden” in the sense that they belong to the past and no longer exist. Clearly, this raises a question as to whether the primitive dimension of time is as physical as we suppose. A lemma used in the formal proof shows that this effect is due to the duration of what may be thought of as a gambler’s bet, without loss of generalization. The bet ends when it is won or lost, analogous to the collapse of a wave function when probabilities become one or zero. Until then, new and empowering information (such as the taking away of a card that is not the ace) does not change the original probabilities. If the profound significance of this is not immediately apparent, a related thought experiment involving a pregnant woman demonstrates that the properties of macroscopic systems are not always completely intrinsic. In this sense, the present paper serves to close the chasm that separates the quantum mechanical from the classical, a subject that continues to be vigorously debated and researched [8] .
References
- Shimojo, S. and Ichikawa, S. (1989) Cognition, 32, 1-24. http://dx.doi.org/10.1016/0010-0277(89)90012-7
- Faulk, R. (1992) Cognition, 43, 197-223. http://dx.doi.org/10.1016/0010-0277(92)90012-7
- Bar-Hillel, M. (1989) Philosophy of Science, 56, 348-358. http://dx.doi.org/10.1086/289493
- Gorroochurn, P. (2012) Bertrand’s Strange Three Boxes. In: Classical Problems of Probability, Wiley, Hoboken. http://dx.doi.org/10.1002/9781118314340.ch18
- Rosenhouse, J. (2009) The Monty Hall Problem. Oxford University Press, NY.
- Fernandez, L. and Piron, R. (1999) Mathematics Magazine, 72, 214-217. http://dx.doi.org/10.2307/2690884
- Allen, A.D. (2015) How to Get Lucky. Publish Green, Minneapolis.
- Zurek, W. (2014) Physics Today, 67, 44-50. http://dx.doi.org/10.1063/PT.3.2550

