Journal of Modern Physics
Vol.5 No.10(2014), Article ID:47434,12 pages
DOI:10.4236/jmp.2014.510096
A Classical Field Theory of Gravity and Electromagnetism
Raymond J. Beach
Lawrence Livermore National Laboratory, Livermore, USA
Email: beach2@llnl.gov
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 April 2014; revised 12 May 2014; accepted 8 June 2014
Abstract
A classical field theory of gravity and electromagnetism is developed. The starting
point of the theory is the Maxwell equations which are directly tied to the Riemann-Christoffel
curvature tensor. This is done through the derivatives of the Maxwell tensor which
are equated to a vector field
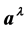 contracted with the curvature tensor, i.e.,
contracted with the curvature tensor, i.e.,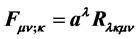 . The electromagnetic portion of the
theory is shown to be equivalent to the classical Maxwell equations with the addition
of a hidden variable. Because the proposed equations describing electromagnetism
and gravity differ from the classical Maxwell-Einstein equations, their ability
to describe classical physics is shown for several situations by direct calculation.
The inclusion of antimatter and its behavior in a gravitational field, and the possibility
of particle-like solutions exhibiting quantized charge, mass and angular momentum
are discussed.
. The electromagnetic portion of the
theory is shown to be equivalent to the classical Maxwell equations with the addition
of a hidden variable. Because the proposed equations describing electromagnetism
and gravity differ from the classical Maxwell-Einstein equations, their ability
to describe classical physics is shown for several situations by direct calculation.
The inclusion of antimatter and its behavior in a gravitational field, and the possibility
of particle-like solutions exhibiting quantized charge, mass and angular momentum
are discussed.
Keywords: Classical Field Theory, Gravitation and Electromagnetism, General Relativity, Antimatter, Antimatter Gravity, Hidden Variable Theories, Riemann Geometry

1. Introduction
Since the introduction of General Relativity, numerous classical field theories
have been proposed which attempt to explain electromagnetism and gravitation in
a unified and geometric framework [1]
[2] . Many of these
previous theories have proceeded by modifying the standard Riemann geometry or by
working in more than 4 dimensions [3]
-[5] . Here a new
and unconventional approach to this problem is developed that offers the possibility
of describing particles with both quantized charge and mass using a continuous 4-dimensional
field theory and without making any modifications to the standard Riemann geometry.
Although the general character of the solutions of the field equations proposed
here is similar to that of General Relativity, the motivation for the equations
is quite different. The motivation of Einstein’s field equations generally starts
with a gravitational weak field analysis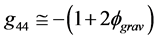 , and then progresses with some judicious
guess work to
, and then progresses with some judicious
guess work to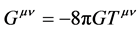 . Here, instead of starting with that weak
field analysis, the algebraic properties of the Riemann-Christoffel tensor are exploited
to relate the Maxwell tensor and its derivatives to the curvature tensor. This leads
naturally to a set of field equations that reduces in their weak field limit to
the classical Maxwell equations and provides an underlying geometric basis for electromagnetism.
Following this approach, the electromagnetic and gravitational field sources are
treated as dynamical variables which when considering particle-like solutions become
quantized through the application of appropriate boundary conditions.
. Here, instead of starting with that weak
field analysis, the algebraic properties of the Riemann-Christoffel tensor are exploited
to relate the Maxwell tensor and its derivatives to the curvature tensor. This leads
naturally to a set of field equations that reduces in their weak field limit to
the classical Maxwell equations and provides an underlying geometric basis for electromagnetism.
Following this approach, the electromagnetic and gravitational field sources are
treated as dynamical variables which when considering particle-like solutions become
quantized through the application of appropriate boundary conditions.
More specifically, a continuous field theory is proposed with dynamical variables
represented by two 2nd-order tensor fields, two vector fields, and two
scalar fields. All of these fields are familiar to classical physics with the exception
of the vector field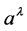 , which is used to couple the derivatives
of the Maxwell tensor to the Riemann-Christoffel curvature tensor. The following
is a list of the theory’s dynamical variables (fields):
, which is used to couple the derivatives
of the Maxwell tensor to the Riemann-Christoffel curvature tensor. The following
is a list of the theory’s dynamical variables (fields):
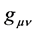 : metric tensor;
: metric tensor;
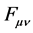 : Maxwell tensor;
: Maxwell tensor;
 : 4-velocity;
: 4-velocity;
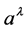 : no counterpart in classical physics, used in
: no counterpart in classical physics, used in
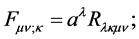
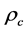 : charge density;
: charge density;
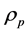 : ponderable mass density.
: ponderable mass density.
The outline of the paper is as follows. After describing the equations of the theory, I show that they are consistent with the requirements of general covariance, i.e., there are four degrees of freedom in the solutions of the dynamical variables of the theory corresponding to the four degrees of freedom in the choice of coordinate system. I then go on to find an exact spherically-symmetric solution for all dynamical variables representing the electric and gravitational fields of a point charge, which is in agreement with the asymptotic forms of these fields predicted by the conventional Maxwell-Einstein theory. A route to finding particle-like solutions having quantized mass, charge and angular momentum is then described, although exact solutions are not found. A discussion of antimatter, how it is included in the theory, and its behavior in gravitational fields are then given. Next I demonstrate a solution representing an electromagnetic plane wave in the weak field limit of the theory. Finally, I discuss the correspondence of the theory to classical electromagnetism. Throughout, emphasis is on the agreement of the proposed theory with the accepted understanding of classical physics (here classical physics refers to Maxwell-Einstein Theory).
Geometric units are used along with a metric tensor having signature [+, +, +, ‒]. Spatial indices run from 1 to 3, with 4 of the time index. For the definitions of the Riemann-Christoffel curvature tensor and the Ricci tensor, the conventions used by Weinberg are followed [6] .1
2. Theory
A covariant theory of gravity and electromagnetism is developed by connecting the
covariant derivatives of the Maxwell tensor
 directly to the Riemann-curvature tensor via contraction with a continuous vector
field
directly to the Riemann-curvature tensor via contraction with a continuous vector
field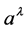 ,
,
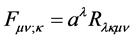 (1)
(1)
The motivations for this equation are the algebraic properties of the Riemann-curvature
tensor. First, the cyclicity of the curvature tensor,
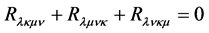 , with (1) immediately gives Maxwell’s source-free equations,
, with (1) immediately gives Maxwell’s source-free equations,
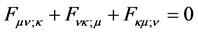 , (2)
, (2)
or equivalently,
 , since
, since
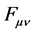 is antisymmetric. Second, Maxwell’s source-containing equations are then introduced
by contracting the μ and κ indices in (1) to obtain
is antisymmetric. Second, Maxwell’s source-containing equations are then introduced
by contracting the μ and κ indices in (1) to obtain
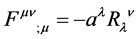 (3)
(3)
and noting that this forces
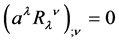 (4)
(4)
since
 vanishes identically by the antisymmetry of
vanishes identically by the antisymmetry of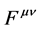 . The conserved vector field
. The conserved vector field
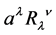 is identified with the conserved electromagnetic current density
is identified with the conserved electromagnetic current density
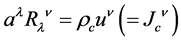 (5)
(5)
where the subscript c stands for charge and is added for clarification and
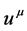 is the ordinary 4-velocity satisfying the normalization
is the ordinary 4-velocity satisfying the normalization
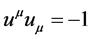 (6)
(6)
In (5),
 is interpreted as the charge density that would be measured
by an observer in the locally inertial coordinate system co-moving with the charge.
Together, (3) and (5) then lead directly to Maxwell’s sourcecontaining equations,
is interpreted as the charge density that would be measured
by an observer in the locally inertial coordinate system co-moving with the charge.
Together, (3) and (5) then lead directly to Maxwell’s sourcecontaining equations,
 (7)
(7)
An expression for
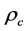 can be derived from (5) and (6) in two equivalent but slightly different forms,
can be derived from (5) and (6) in two equivalent but slightly different forms,
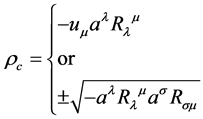 (8)
(8)
which will both be useful when looking for specific solutions. To complete the theory, a conserved energymomentum tensor is added,
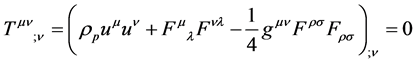 (9)
(9)
where
 is the ponderable mass density and so always nonnegative. Contracting (9) with
is the ponderable mass density and so always nonnegative. Contracting (9) with
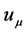 gives
gives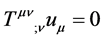 , which leads directly to
, which leads directly to
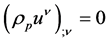 (10)
(10)
identifying
 as a locally conserved quantity. Combining (9) and (10) then gives
as a locally conserved quantity. Combining (9) and (10) then gives
 (11)
(11)
the Lorentz Force Law. The particular form of the energy-momentum tensor in (9) was chosen to ensure (10) and (11) as consequences. As described in the next section, the theory is logically consistent from the stand point of general covariance without need to impose any conditions on the stress-energy tensor beyond it being divergence free and of the form given in (9).
3. Logical Consistency and Completeness of Theory
The logical consistency and completeness of the theory is manifest in 22 independent relations that are used to determine the 26 dynamical fields of the theory. The 4-degrees of freedom in the determination of the dynamical variables are a result of general covariance. The dynamical variables of the theory are given in Table1
The equations of the theory are given in Table2
But not all of the equations of the theory listed in Table 2 are independent. Dependent equations which are derived from the equations in Table 2 are listed in Table3
The 11 dependent equations listed in Table 3, when applied against the 33 equations of the theory listed in Table 2, give a total of 22 independent equations.
4. Integrability Conditions
The approach presented here for electromagnetism and gravity departs from the standard Maxwell-Einstein description in the mixed system of first order partial differential equations that are used to describe the Maxwell tensor (1). It is not obvious at this point that (1) allows any solutions to exist due to the integrability conditions
Total = 26.
Table 2. Equations of theory.
Total = 33.
Table 3. Dependent equations.
Total = 11.
that must be satisfied by such a system for a solution to exist [7] . Although there are several ways of stating what these integrability conditions are, perhaps the simplest is given by
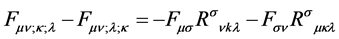 (12)
(12)
which is arrived at using the commutation relations for covariant derivatives. Using
(1) to substitute for
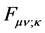 in (12) gives
in (12) gives
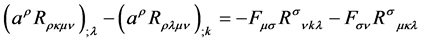 (13)
(13)
which can be interpreted as conditions that are automatically satisfied by any solution
consisting of expressions for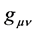 ,
,
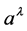 and
and
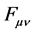 that satisfy (1). In addition to the integrability conditions represented by (13),
subsequent integrability conditions can be derived by repeatedly taking the covariant
derivative of (13) and substituting in the resulting equation for
that satisfy (1). In addition to the integrability conditions represented by (13),
subsequent integrability conditions can be derived by repeatedly taking the covariant
derivative of (13) and substituting in the resulting equation for
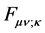 using (1). The question that now arises is this: are these integrability conditions
so restrictive that perhaps no solutions exist to the proposed theory? If so, and
no solutions exist, then the theory is not interesting. But as will be shown in
the next section, formal solutions satisfying the theory and representing particle-like
fields which are in agreement with the classical Maxwell-Einstein theory in their
asymptotic limit do exist. Additionally, radiative solutions valid in the weak field
limit of the theory and representing electromagnetic plane waves are shown to exist.
The existence of these formal solutions provides one of the motivations for further
investigation of the theory.
using (1). The question that now arises is this: are these integrability conditions
so restrictive that perhaps no solutions exist to the proposed theory? If so, and
no solutions exist, then the theory is not interesting. But as will be shown in
the next section, formal solutions satisfying the theory and representing particle-like
fields which are in agreement with the classical Maxwell-Einstein theory in their
asymptotic limit do exist. Additionally, radiative solutions valid in the weak field
limit of the theory and representing electromagnetic plane waves are shown to exist.
The existence of these formal solutions provides one of the motivations for further
investigation of the theory.
5. Spherically Symmetric Solution
In this section solutions having spherical symmetry are investigated. Under these
conditions, it is demonstrated that the Reissner-Nordstrom metric with an appropriate
choice for
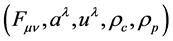 is a formal solution of the theory, i.e., all equations in
Table 2 are satisfied. Although the presentation in this section is purely
formal, it is included here for several reasons. First, if the theory could not
describe the asymptotic electric and gravitational fields of a point charge it would
be of no interest on physical grounds. Second, the presented theory requires the
solution of a mixed system of first order partial differential equations, a system
that may be so restrictive that no solutions exist, and so at least a mechanical
outline of one methodology to demonstrate a solution is warranted.
is a formal solution of the theory, i.e., all equations in
Table 2 are satisfied. Although the presentation in this section is purely
formal, it is included here for several reasons. First, if the theory could not
describe the asymptotic electric and gravitational fields of a point charge it would
be of no interest on physical grounds. Second, the presented theory requires the
solution of a mixed system of first order partial differential equations, a system
that may be so restrictive that no solutions exist, and so at least a mechanical
outline of one methodology to demonstrate a solution is warranted.
Starting with the Reissner-Nordstrom metric [8] ,
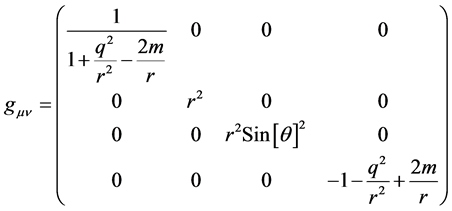 (14)
(14)
and a guess for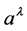 ,
,
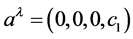 (15)
(15)
where
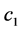 is a yet to be determined constant,
is a yet to be determined constant,
 is determined from the second form of (8) to be
is determined from the second form of (8) to be
 (16)
(16)
where the positive root has been arbitrarily chosen. I’ll come back to this point
later, but for now note that only nonnegative charge density is allowed by the theory
with this choice for the root of (8). Using (5),
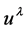 is then found to be
is then found to be
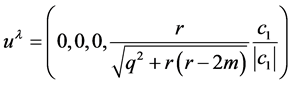 (17)
(17)
The next step is to satisfy (1) by solving for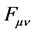 . Rather than tackling this head on and
trying to find a solution to (1), I will solve the integrability Equations (13),
which are linear in
. Rather than tackling this head on and
trying to find a solution to (1), I will solve the integrability Equations (13),
which are linear in
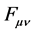 for
for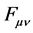 . Solving (13) in this manner, it is found that all
the integrability equations are satisfied for
. Solving (13) in this manner, it is found that all
the integrability equations are satisfied for
 given by
given by
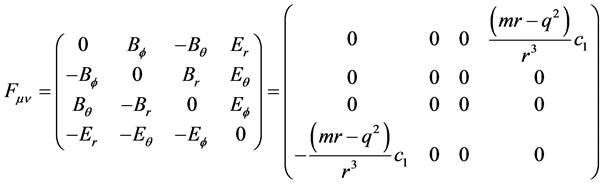 (18)
(18)
Choosing
 then gives an electric field that agrees with the Coulomb field of a point charge
to leading order in
then gives an electric field that agrees with the Coulomb field of a point charge
to leading order in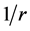 . It is straightforward to substitute (18)
into (1) and verify that (1) is now satisfied. The last remaining equation of the
theory, the conserved energy-momentum Equation (9), is satisfied for
. It is straightforward to substitute (18)
into (1) and verify that (1) is now satisfied. The last remaining equation of the
theory, the conserved energy-momentum Equation (9), is satisfied for
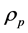 given by
given by
 . (19)
. (19)
This demonstrates that the values for the field quantities
 given in this section are an exact solution to the theory’s equations.
given in this section are an exact solution to the theory’s equations.
6. Quantization
The last step in the solution above in which the conserved energy-momentum Equation
(9) was solved for
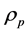 demonstrates that formal solutions to the theory do
exist. Because
demonstrates that formal solutions to the theory do
exist. Because
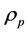 is a dynamical field of the proposed theory an additional physical constraint can
be imposed on
is a dynamical field of the proposed theory an additional physical constraint can
be imposed on
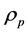 by requiring that it be self-consistent with the mass of the particle being modeled.
This self-consistent mass can be determined by the gravitational field far from
the particle, i.e.,
by requiring that it be self-consistent with the mass of the particle being modeled.
This self-consistent mass can be determined by the gravitational field far from
the particle, i.e.,
 for large r. This constraint can be formulated quite
generally for the static-metric, particle-like solutions being considered here as
the following boundary condition,
for large r. This constraint can be formulated quite
generally for the static-metric, particle-like solutions being considered here as
the following boundary condition,
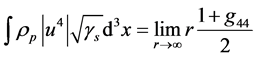 , (20)
, (20)
where
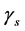 is the determinant of the spatial metric tensor given by
[9] ,
is the determinant of the spatial metric tensor given by
[9] ,
 . (21)
. (21)
In (21) i and j vary over the spatial indices only, and in (20) the factor
 appears in the integrand because it is the locally measured mass density where
appears in the integrand because it is the locally measured mass density where
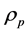 is the mass density that would be measured in the locally inertial coordinate system
that is co-moving with it. The same type of self-consistency argument used above
for quantizing mass can also be applied to charge, leading to quantized charge solutions.
For the spherical coordinate system being considered here, the appropriate boundary
condition on charge is
is the mass density that would be measured in the locally inertial coordinate system
that is co-moving with it. The same type of self-consistency argument used above
for quantizing mass can also be applied to charge, leading to quantized charge solutions.
For the spherical coordinate system being considered here, the appropriate boundary
condition on charge is
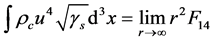 . (22)
. (22)
For the spherically symmetric solution investigated in the previous section, the
LHS of both (20) and (22) diverge leaving no hope for satisfying these boundary
conditions. The upshot of this observation is that while representing a solution
that describes the gravitational and electrical fields of a point charge and formally
satisfying the equations of the theory in Table 2,
the Reissner-Nordstrom metric solution cannot represent a physically allowed particle-like
solution. The possibility of finding solutions that satisfy both the equations of
the theory in Table 2 and the quantized mass and
charge boundary conditions (20) and (22) remains an open question at this point.
The reason for the absolute value of
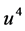 in boundary condition (20) for mass but not in boundary condition (22) for charge
is driven by the symmetries of the equations of the theory in
Table 2, and will be discussed more fully in the next section. Finally,
if one goes to more generalized metrics that include nonzero angular momentum about
an axis (cylindrically symmetric solutions) and so the possibility of magnetic fields,
the line of thought used above to quantize the mass and charge of the particle can
also be used to quantize its angular momentum.
in boundary condition (20) for mass but not in boundary condition (22) for charge
is driven by the symmetries of the equations of the theory in
Table 2, and will be discussed more fully in the next section. Finally,
if one goes to more generalized metrics that include nonzero angular momentum about
an axis (cylindrically symmetric solutions) and so the possibility of magnetic fields,
the line of thought used above to quantize the mass and charge of the particle can
also be used to quantize its angular momentum.
7. Antimatter
The distinction between matter and antimatter in the theory is carried by the 4-velocity
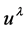 and the value that it takes on in the locally inertial co-moving coordinate system.
In this coordinate system matter will have
and the value that it takes on in the locally inertial co-moving coordinate system.
In this coordinate system matter will have
 and antimatter will have
and antimatter will have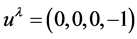 . The spherically symmetric solution
just investigated provides an illustration of this. In that solution, the value
of the constant c1 was chosen to be q/m. If q/m > 0, then the 4th
component of
. The spherically symmetric solution
just investigated provides an illustration of this. In that solution, the value
of the constant c1 was chosen to be q/m. If q/m > 0, then the 4th
component of
 in (17) is positive, corresponding to matter. If, on the other hand, q/m < 0, then
the 4th component of
in (17) is positive, corresponding to matter. If, on the other hand, q/m < 0, then
the 4th component of
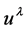 is negative, corresponding to antimatter. This is the analogue of the view today
that a particle’s antiparticle is the particle moving backwards through time [10] . With these definitions for the 4-velocity of matter
and antimatter, charged ponderable mass density can annihilate similarly charged
ponderable antimass density and satisfy both the local conservation of charge (4)
and ponderable mass (10). Because total massenergy is conserved (9), the annihilation
of ponderable matter and antimatter must be accompanied by the generation of electromagnetic
energy, the only other available energy channel in the theory.
is negative, corresponding to antimatter. This is the analogue of the view today
that a particle’s antiparticle is the particle moving backwards through time [10] . With these definitions for the 4-velocity of matter
and antimatter, charged ponderable mass density can annihilate similarly charged
ponderable antimass density and satisfy both the local conservation of charge (4)
and ponderable mass (10). Because total massenergy is conserved (9), the annihilation
of ponderable matter and antimatter must be accompanied by the generation of electromagnetic
energy, the only other available energy channel in the theory.
The following discussion further illuminates the definitions of matter and antimatter
proposed above. For definiteness in what follows I will require
 always, corresponding to choosing the positive root in the second form of (8). With
this requirement of only nonnegative charge density allowed by the theory, it will
be useful to develop a test particle formalism to illustrate how test particles
with an apparently negative charge can be handled in a self-consistent way. To do
this I introduce a parameter s that takes on the value +1 for matter test particles
and −1 for antimatter test particles
always, corresponding to choosing the positive root in the second form of (8). With
this requirement of only nonnegative charge density allowed by the theory, it will
be useful to develop a test particle formalism to illustrate how test particles
with an apparently negative charge can be handled in a self-consistent way. To do
this I introduce a parameter s that takes on the value +1 for matter test particles
and −1 for antimatter test particles
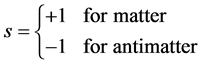 (23)
(23)
Consistent with the above definitions for matter and antimatter, the transformation from a test particle’s proper time interval dτ to a coordinate time interval dt is given by
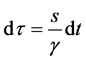 (24)
(24)
and so the 4-velocity of a test particle is related to the ordinary 3-space velocity
 by
by
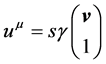 (25)
(25)
where γ has the usual definition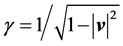 . Now consider a region with an externally
defined electromagnetic field
. Now consider a region with an externally
defined electromagnetic field
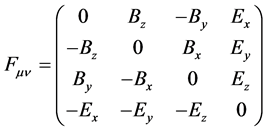 (26)
(26)
and with no, or at least a very weak, gravitational field so that
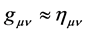 and
and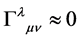 . Starting with the Lorentz Force Law (11) we have
. Starting with the Lorentz Force Law (11) we have
 (27)
(27)
which on the last line above ends up at the conventional form of the Lorentz Force Law except for the extra factor of s on the RHS. This extra factor of s in (27) gives the product s.ρc the appearance of a negative charge density for antimatter and a positive charge density for matter.
The equations of the theory in Table 2 exhibit C-symmetry (charge conjugation symmetry), as for any matter solution there exists a corresponding antimatter solution via the field transformation
 (28)
(28)
which leaves all equations in Table 2 unchanged.
Using the already investigated Reissner-Nordstrom metric solution and the C-symmetry
exhibited by the equations of the theory under transformation (28) one can now make
predictions about the behavior of antimatter in an external gravitational field—is
it attracted or repelled? As noted above in the investigation of the Reissner-Nordstrom
metric solution, the difference between matter and antimatter solutions is dictated
by the choice of sign of the charge-to-mass ratio q/m. Examining the ReissnerNordstrom
metric (14) and noting that q appears always raised to the second power while m
appears always to the first power (also true for the Kerr-Newman metric), the only
way to ensure that matter solutions will have corresponding antimatter solutions
with the same metrical structure is to require that the transformation from matter
to corresponding antimatter solutions (changing the sign of the charge-to-mass ratio)
be accomplished via the metric transformation
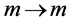 and
and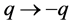 . This observation is the reason that the absolute value
of
. This observation is the reason that the absolute value
of
 is taken in the boundary condition (20) for mass but not in the boundary condition
(22) for charge, and further motivates the requirement that ρp be always
nonnegative. To answer the question of whether antimatter is attracted or repelled
by a gravitational field, I go again to the Lorentz Force Law (11), but this time
assume there is no electromagnetic field present at the location of the test particle,
just a gravitational field corresponding to a Schwarzschild metric generated by
a central mass m corresponding to either matter or antimatter, that is a distance
r from the test particle, also matter or antimatter, which I take to be initially
at rest. In this case the equation of motion of the test particle reduces to a geodesic
trajectory as expected
is taken in the boundary condition (20) for mass but not in the boundary condition
(22) for charge, and further motivates the requirement that ρp be always
nonnegative. To answer the question of whether antimatter is attracted or repelled
by a gravitational field, I go again to the Lorentz Force Law (11), but this time
assume there is no electromagnetic field present at the location of the test particle,
just a gravitational field corresponding to a Schwarzschild metric generated by
a central mass m corresponding to either matter or antimatter, that is a distance
r from the test particle, also matter or antimatter, which I take to be initially
at rest. In this case the equation of motion of the test particle reduces to a geodesic
trajectory as expected
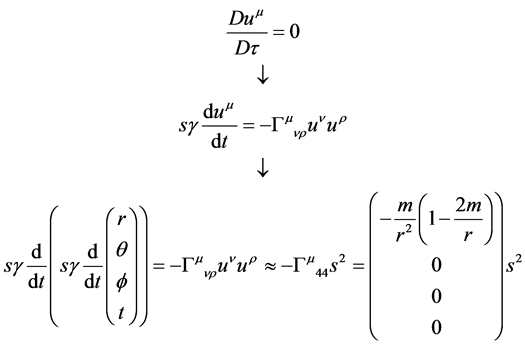 (29)
(29)
where in the last line above I have approximated the RHS using the initial at rest
value of
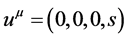 and I have used the fact that the only nonzero
and I have used the fact that the only nonzero
 in a Schwarzchild metric is
in a Schwarzchild metric is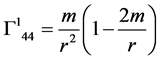 . Further simplifying the first component
of the last line in (29) by noting that initially
. Further simplifying the first component
of the last line in (29) by noting that initially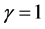 , gives
, gives
 (30)
(30)
independent of s, and so demonstrating that the proposed theory predicts that both matter and antimatter test particles will be attracted by a gravitational field generated by either matter or antimatter. The prediction of (30) that the gravitational interaction between matter and antimatter is mutually attractive is in contradiction to recent predictions based on the classical general relativity equations and their assumed CPT invariance [11] . There has recently been much interest in this issue due to possible explanations of dark matter [12] and dark energy density [13] . The planned AEgIS experiments (Antimatter Experiment: gravity, Interferometer, Spectroscopy) at CERN to measure the gravitational interaction between matter and antimatter may soon provide an experimental determination of this issue [14] .
8. Electromagnetic Plane Wave
In this section I investigate approximate solutions that represent electromagnetic plane waves. Throughout I work in the weak field limit with
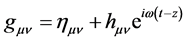 (31)
(31)
where
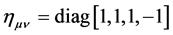 and
and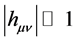 , and I only retain the terms to 1st order
in the h’s. The coordinate system used is
, and I only retain the terms to 1st order
in the h’s. The coordinate system used is , and I assume a plane wave polarized
in the x-direction and propagating in the +z-direction. This situation is described
by the following Maxwell tensor,
, and I assume a plane wave polarized
in the x-direction and propagating in the +z-direction. This situation is described
by the following Maxwell tensor,
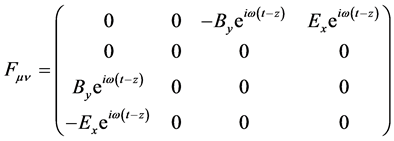 (32)
(32)
To begin, I guess at a form for ,
,
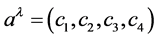 (33)
(33)
where c1, c2, c3 and c4 are yet to be
determined constants. Next I impose (4),
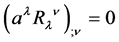 , which gives
, which gives
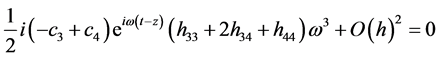 (34)
(34)
There are two ways to solve (34), either
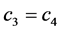 or
or , but in the end it will not matter which is chosen,
as both conditions will be required. Now imposing (1), we arrive at a series of
constraints on the h’s and c’s that must be satisfied to the 1st order
in h. Rather than reproduce all of these equations here, I just give the results
below, which are straightforward to verify by direct substitution.
, but in the end it will not matter which is chosen,
as both conditions will be required. Now imposing (1), we arrive at a series of
constraints on the h’s and c’s that must be satisfied to the 1st order
in h. Rather than reproduce all of these equations here, I just give the results
below, which are straightforward to verify by direct substitution.
 (35)
(35)
In summary, the following metric tensor
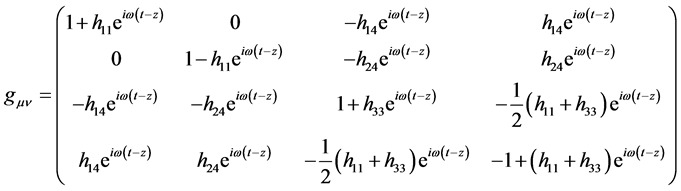 (36)
(36)
with
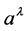 given by
given by
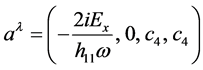 (37)
(37)
describes an electromagnetic plane wave polarized in the x-direction and propagating
in the +z-direction with electric field amplitude Ex. At this point the
values of h14, h24, h33, and c4 in (36)
and (37) are not restricted beyond the small field approximation for the h’s. The
solution has the interesting property that the value of h11 is only required
to be nonzero to yield a physical solution for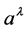 , but beyond that is unrestricted except
for the weak field approximation if no further conditions are placed on
, but beyond that is unrestricted except
for the weak field approximation if no further conditions are placed on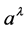 .
.
9. Discussion
Taking a starting point that is distinctly different from that of the Maxwell-Einstein equations, the theory proposed here has been shown to agree with the predictions of the Maxwell-Einstein equations in the classical physics regime:
Ÿ Equations (2)
 and (7)
and (7)
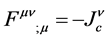 of the theory, are in the weak field limit exactly those
of classical electromagnetism on Minkowski spacetime and so in the weak field limit
the proposed theory corresponds to the classical Maxwell theory as already demonstrated
for several physical situations. However, the proposed theory does not correspond
exactly to classical electromagnetism because the Maxwell tensor
of the theory, are in the weak field limit exactly those
of classical electromagnetism on Minkowski spacetime and so in the weak field limit
the proposed theory corresponds to the classical Maxwell theory as already demonstrated
for several physical situations. However, the proposed theory does not correspond
exactly to classical electromagnetism because the Maxwell tensor
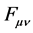 is directly tied to the metric tensor and vice versa through (1). This is substantially
different than the case in classical Maxwell-Einstein theory where the electromagnetic
fields are at most coupled to the metric tensor through the energy-momentum tensor
in Einstein’s General Relativity
is directly tied to the metric tensor and vice versa through (1). This is substantially
different than the case in classical Maxwell-Einstein theory where the electromagnetic
fields are at most coupled to the metric tensor through the energy-momentum tensor
in Einstein’s General Relativity . An interesting observation is that if
one only assumes knowledge of Equations (2) and (7) but not (1), as in classical
electromagnetism, then the view from the perspective of the theory proposed here
is that the classical description is incomplete, i.e., Maxwell’s equations are incomplete
due to the hidden variable
. An interesting observation is that if
one only assumes knowledge of Equations (2) and (7) but not (1), as in classical
electromagnetism, then the view from the perspective of the theory proposed here
is that the classical description is incomplete, i.e., Maxwell’s equations are incomplete
due to the hidden variable
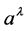 in (1),
in (1),
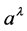 having no direct correspondence in classical physics.
having no direct correspondence in classical physics.
Ÿ Solutions representing the fields of point charges are shown to be described by the theory with electric fields in agreement to leading order in 1/r with those calculated using Maxwell’s equations, and their gravitational fields in agreement with those calculated using the Reissner-Nordstrom metric and General Relativity.
Ÿ Electromagnetic plane waves are shown to be allowed weak field solutions of the theory, and because Maxwell’s equations are contained in the theory, the interaction of charged matter with electromagnetic fields is also described by the theory.
Ÿ Although not presented in this manuscript, by following the same procedure as outlined for the ReissnerNordstrom metric in Section 5, one can show that the Kerr-Newman metric satisfies the equations of the theory to leading order in 1/r, demonstrating that the theory also allows the asymptotic field descriptions of a point charge superimposed on a magnetic dipole to leading order in 1/r.
It is in the sense that the above points encompass classical physics that it can
be argued the theory correctly describes classical physics. However, the theory
differs from the classical physics description in that the source terms of both
gravitational fields and electromagnetic fields are deterministically described
as dynamic variables (fields) by the theory. The theory as presented obeys the rigid
requirements of being logically complete in that the all of the theory’s dynamic
variables (fields) are given up to the requirements imposed by general covariance.
This internal logic is manifest with the introduction of the vector field
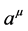 that has no counterpart in classical physics, but which is a well hidden variable
in most circumstances. Specifically
that has no counterpart in classical physics, but which is a well hidden variable
in most circumstances. Specifically
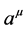 is hidden in the classical physics regime considered above by the identification
of it with the charge current density given in (5), i.e., with that identification
the theory yields the standard Maxwell equations. The fact that
is hidden in the classical physics regime considered above by the identification
of it with the charge current density given in (5), i.e., with that identification
the theory yields the standard Maxwell equations. The fact that
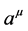 is so well hidden in what is a fully deterministic theory that replicates our understanding
of physics in the classical regime, and the fact that
is so well hidden in what is a fully deterministic theory that replicates our understanding
of physics in the classical regime, and the fact that
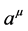 is intimately tied to the charge density of particle-like solutions (5) makes it
enticing to consider it as a bridge to quantum mechanical considerations.
is intimately tied to the charge density of particle-like solutions (5) makes it
enticing to consider it as a bridge to quantum mechanical considerations.
A remarkable feature of the theory is that the gravitational field of particles is in agreement with that of General Relativity; this in spite of the fact that for the theory presented within the Riemann-Christoffel curvature tensor is fundamentally tied to the Maxwell tensor, but in General Relativity it is fundamentally tied the energymomentum tensor. This point is worth emphasizing: both conventional General Relativity and the theory presented within allow static-metric solutions having the same character and representing point-like sources. Differences between the presented theory and General Relativity start to become evident when considering non static metrics with distributed sources. For example, the Robertson-Walker metric is a solution of both the theory presented within and General Relativity, representing an isotropic and homogeneous universe in both cases. However, because the theory presented within does not directly tie the Riemann-Christoffel curvature tensor to the energy-momentum tensor (as is done in General Relativity) there is no constraint placed on the scale parameter of the Robertson-Walker metric, i.e., no analogue to the Friedmann equation. Although not investigated further here, this difference between General Relativity and the theory within may be a motivation for further study of the theory, as the inability of General Relativity and the Standard Model of particle physics to correctly describe astronomical observations beyond the scale of our own solar system has recently served as an impetus to consider modifications to General Relativity [15] .
One of the most interesting aspects of the theory put forth here is its capability
to give a self-consistent description of matter and antimatter from a classical
(non-quantum) field theory. The requirement that both ponderable mass and charge
density, representing either matter or antimatter, be nonnegative always (charge
density is required to be nonnegative if we take the positive root of Equation (8))
is accommodated by the theory with the appropriate sign convention for
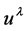 as previously discussed. With this sign convention, the definition of matter and
antimatter is forced and unambiguous to be consistent with observation and essentially
boils down to saying that matter has positive charge q and antimatter has negative
charge q, where q is defined by
as previously discussed. With this sign convention, the definition of matter and
antimatter is forced and unambiguous to be consistent with observation and essentially
boils down to saying that matter has positive charge q and antimatter has negative
charge q, where q is defined by
 (38)
(38)
This continuous field description of matter and antimatter potentially allows for particle-like solutions containing separated regions of matter and antimatter configured such that they are dynamically stable. Any such particle solution will continue to have an accompanying antiparticle solution in the sense of the C-transformation given by (28), but both of these C-symmetry related solutions will consist of separated regions of ponderable matter and antimatter. Charged particles which consist of both matter and antimatter regions would then correspond to solutions in which the matter and antimatter regions are not balanced so as to give the net observed charge of the particle. This leads to the interesting possibility that a charged neutral atom is comprised of equal quantities of continuous matter and antimatter with the implication being the universe is locally balanced in matter and antimatter. Although very speculative without specific solutions to refer to, the discussion in this paragraph is included to make the point that the association of matter with positive q and antimatter with negative q is not in contradiction with observation.
10. Conclusions
The proposed classical field theory of gravity and electromagnetism developed here
encompasses classical physics but departs from the classical Maxwell-Einstein theory
in two significant ways. First, the equation
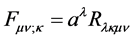 is introduced which ties the derivatives of the Maxwell tensor to the Riemann curvature
tensor through a vector field
is introduced which ties the derivatives of the Maxwell tensor to the Riemann curvature
tensor through a vector field
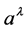 that has no counterpart in classical physics. Second, beyond the requirement that
the energy-momentum tensor is conserved
that has no counterpart in classical physics. Second, beyond the requirement that
the energy-momentum tensor is conserved
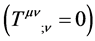 and consists of a ponderable mass and electromagnetic term (9), there is no need
to put any constraint on it as it is done in General Relativity, i.e.,
and consists of a ponderable mass and electromagnetic term (9), there is no need
to put any constraint on it as it is done in General Relativity, i.e.,
 is not required. Adding to this, the definition of the
conserved electromagnetic charge current (5) and a local normalization requirement
on the vector field
is not required. Adding to this, the definition of the
conserved electromagnetic charge current (5) and a local normalization requirement
on the vector field
 (6), defines the theory. The theory is shown to be logically consistent from the
standpoint of general covariance, with 22 independent equations determining the
26 dynamical fields
(6), defines the theory. The theory is shown to be logically consistent from the
standpoint of general covariance, with 22 independent equations determining the
26 dynamical fields
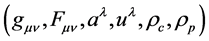 that comprise the theory. In general the theory is more
restrictive in its allowed solutions than the classical Maxwell-Einstein equations
due to the mixed system of partial differential Equations (1) and their accompanying
integrability conditions (12) which must be satisfied. Boundary conditions on any
physically allowed particle-like solutions impose quantization conditions on the
mass, charge and angular momentum of the solution, and the inclusion of antimatter
and its behavior in a gravitational field is straightforward. Finally, the vector
field
that comprise the theory. In general the theory is more
restrictive in its allowed solutions than the classical Maxwell-Einstein equations
due to the mixed system of partial differential Equations (1) and their accompanying
integrability conditions (12) which must be satisfied. Boundary conditions on any
physically allowed particle-like solutions impose quantization conditions on the
mass, charge and angular momentum of the solution, and the inclusion of antimatter
and its behavior in a gravitational field is straightforward. Finally, the vector
field , which has no counterpart in classical physics, plays
the part of a hidden variable in the classical physics regime.
, which has no counterpart in classical physics, plays
the part of a hidden variable in the classical physics regime.
Because I have not offered any complete particle-like solutions satisfying the boundary conditions (20) and (22), the presented theory must be considered unproven at this point. However, the theory’s simplicity and logical consistency from the standpoint of general covariance, its ability to correctly describe the asymptotic gravitational and electromagnetic fields of a point charge, the possible impact it may have on hidden variable theories, and its ability to describe classical physics may make it interesting for further investigation.
The genesis of the work presented here was reported in a 1999 publication in which
a different interpretation of (1) was proposed and an attempt was made to integrate
it into classical General Relativity,
 [16] .
[16] .
This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344.
References
- Goenner, H.F.M. (2004) Living Reviews in Relativity, 7. http://www.livingreviews.org/lrr-2004-2.
- Sachs, M. (1999) Nuovo Cimento Della Societa Italiana Di Fisica B—Basic Topics in Physics, 114, 123-126.
- Elyasi, N. and Boroojerdian, N. (2011) International Journal of Theoretical Physics, 50, 850-860.http://dx.doi.org/10.1007/s10773-010-0622-9
- Wesson, P.S. and Ponce de Leon, J. (1992) Journal of Mathematical Physics, 33, 3883-3887.http://dx.doi.org/10.1063/1.529834
- Overduin, J.M. and Wesson, P.S. (1997) Physics Reports, 283, 303-378. http://dx.doi.org/10.1016/S0370-1573(96)00046-4
- Weinberg, S. (1972) Gravitation and Cosmology. John Wiley & Sons, New York.
- Eisenhart, L.P. (1947) An Introduction to Differential Geometry, Chapter 23: Systems of Partial Differential Equations of the First Order, Mixed Systems. Princeton University Press, Princeton.
- Misner, C., Thorne, K. and Wheeler, J. (1970) Gravitation. W.H. Freeman and Company, San Francisco, 840.
- Landau, L.D. and Lifshitz, E.M. (1975) The Classical Theory of Fields. 4th Edition, Pergamon Press, New York, 235.
- Feynman, R.P. (1949) Physical Review, 76, 749-759. http://dx.doi.org/10.1103/PhysRev.76.749
- Villata, M. (2011) EPL, 94, 20001-p1-20001-p4.
- Hajdukovic, D.S. (2011) Astrophysics and Space Science, 334, 215-218. http://dx.doi.org/10.1007/s10509-011-0744-4
- Hajdukovic, D.S. (2010) Astrophysics and Space Science, 330, 1-5. http://dx.doi.org/10.1007/s10509-010-0387-x
- Ferragut, R., et al. (2011) Canadian Journal of Physics, 89, 17-24. http://dx.doi.org/10.1139/P10-099
- Starkman, G.D. (2012) Philosophical Transactions of the Royal Society A, 369, 5018-5041. http://dx.doi.org/10.1098/rsta.2011.0292
- Beach, R.J. (1999) Physics Essays, 12, 457-467. http://dx.doi.org/10.4006/1.3025404
NOTES

1The definition of the Riemann-Christoffel curvature tensor is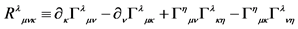 , and the definition of the Ricci tensor is
, and the definition of the Ricci tensor is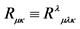 .
.


