Received 4 August 2014; revised 1 September 2014; accepted 26 September 2014

ABSTRACT

The pairon field operator 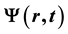evolves, following Heisenberg’s equation of motion. If the Hamiltonian H contains a condensation energy and a repulsive point-like interparticle interaction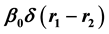, , 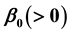the evolution equation for is non-linear, from which we derive the Ginzburg-Landau (GL) equation: 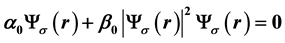for the GL wave function, 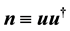where denotes the state of the condensed Cooper pairs (pairons), and n the pairon density operator (u and are kind of square root density operators). The GL equation with 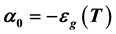holds for all temperatures below the critical temperature T_c, where 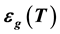is the T-dependent pairon energy gap. Its solution yields the condensed pairon density. The T-dependence of the expansion parameters near T_c obtained by GL:, 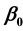= constant is confirmed.

Keywords:

Ginzburg-Landau Equation, Complex-Order Parameter, Coherent Length, Cooper Pair (Pairon), Pairon Density Operator, T-Dependent Pairon Energy Gap

1. Introduction

In 1950 Ginzburg and Landau (GL) [1] proposed a revolutionary idea that below the critical temperature T_c a superconductor has a complex order parameter (also known as a GL wave function) just as a ferromagnet possesses a real order parameter (spontaneous magnetization). Based on Landau’s theory of second-order phase transition [2] , GL expanded the free energy density of a superconductor in powers of small and:

, (1)

where, and are constants, and is the superelectron mass. To include the effect of a magnetic field, they used a quantum replacement:

, (2)

where A is a vector potential generating, and added a magnetic energy term. The integral of the free energy density over the sample volume Ω gives the Helmholtz free energy F. After minimizing F with variation in and A_j, GL obtained two equations:

, (3)

, (4)

with the density condition:

, (5)

where j is the current density.

The superelectron model has difficulties. Since electrons are fermions, no two electrons can occupy the same particle state by Pauli’s exclusion principle. Cooper [3] introduced Cooper pairs in 1956. Bardeen, Cooper and Schrieffer (BCS) published a classic paper [4] on the superconductivity in 1957 based on the phonon exchange attraction between two electrons. The center-of-mass (CM) of Cooper pairs (pairons) move as bosons, which is shown in Section 2. We view that the Bose-condensed pairons can generate the superconducting state. We modify the density condition (5) to

. (6)

Equation (3) is the celebrated Ginzburg-Landau equation, which is quantum mechanical and nonlinear. Since the smallness of is assumed, the GL equation was thought to hold only near T_c,. Below T_c there is a supercondensate whose motion generates a supercurrent and whose presence generates gaps in the elementary excitation energy spectra. The GL wave function represents the quantum state of this supercondensate.

In the present work, we derive the GL wave equation microscopically and show that the GL equation is valid for all temperature below T_c.

2. Moving Cooper Pairs (Pairons)

Fujita, Ito and Godoy in their book [5] discussed the moving pairons. We briefly summarize their theory and main results here. The energy of a moving pairon can be obtained from

(7)

which is Cooper’s equation, Equation (1) of his 1956 Physical Review [3] . The prime on the k'-integral means the restriction on the integration domain arising from the phonon-exchange attraction, see below. We note that the net momentum q is a constant of motion, which arises from the fact that the phonon exchange is an internal process, and hence cannot change the net momentum q. The pair wave functions are coupled with respect to the other variable k, meaning that the exact (or energy-eigenstate) pairon wavefunctions are superpositions of the pair wavefunctions.

Equation (7) can be solved as follows. We assume that the energy is negative:

. (8)

Then,. Rearranging the terms in Equation (7) and dividing it by

, we obtain

. (9)

Here

(10)

is k-independent. Introducing Equation (9) in Equation (7), and dropping the common factor, we obtain

. (11)

We now assume a free electron model. The Fermi surface is a sphere of the radius (momentum):

, (12)

where m₁ represents the effective mass of an electron. The energy is given by

. (13)

The prime on the k-integral in Equation (11) means the restriction:

. (14)

We may choose the polar axis along q as shown in Figure 1. The integration with respect to the azimuthal angle simply yields the factor 2π. The k-integral can then be expressed by

(15)

where k_D is given by

(16)

After performing the integration and taking the small-q and small- limits, we obtain

, (17)

where the pairon ground-state energy w₀ is given by

. (18)

As expected, the zero-momentum pairon has the lowest energy. The excitation energy is continuous with no energy gap. Equation (17) was first obtained by Cooper (unpublished) and it is recorded in Schrieffer’s book (Ref. [6] , Equations (2)-(15)). The energy w_q increases linearly with momentum for small q. This behavior arises since the pairon density of states is strongly reduced with increasing momentum q and dominates the q²-increase of the kinetic energy. This linear dispersion relation means that a pairon moves like a massless particle with a common speed.

The center-of-mass (CM) of pairons move as bosons. We can show this as follows. Second-quantized operators for a pair of “electrons” (i.e., “electron” pairons) are defined by

(19)

where c’s and’s satisfy the Fermi anti-commutation rules:

. (20)

Using Equation (20) we compute commutation relations for pair operators and obtain

(21)

(22)

, (23)

where

(24)

are number operators for electrons. Using Equations (19)-(24), we obtain

. (25)

Hence, indicating that the eigenvalues of are or 1. Thus, the number operator in the representation with both and specified, has the eigenvalues 0 or 1.

We now introduce

, (26)

and calculate and obtain

, (27)

from which it follows straightforwardly that the eigenvalues of are: [7]

(28)

with the eigenstates

. (29)

3. Ginzburg-Landau Equation at 0 K

Let us take a three dimensional (3D) superconductor such as tin (Sn) and lead (Pb). Both metals form face-cen- tered cubic (fcc) crystals. They are in superconducting states at 0 K.

The system ground-state wave function is a constant in the normalization volume Ω and vanishes at the boundary:

(30)

We may assume a periodic rectangular-box with side-lengths along the cubic lattice,

(31)

where a is the lattice constant.

We introduce a one-body density operator n and the density matrix n_ab for the treatment of a many-particle system. The density operator n can be expanded in the form:

(32)

where denote the relative probabilities that particle states are occupied. It is customary to adopt the following normalization condition:

, (33)

where the symbol “tr” means a one-body trace and N is the particle number. The density operator n is Hermitean:

. (34)

Let us introduce kind of a square root density operator u such that

. (35)

This u is not Hermitean but is. We will show that the revised G-L wave function is connected with

, (36)

where denotes the condensed pairon state. For a running ring super current [8] we may choose

, (37)

where L is the ring circumference. The are very small numbers. The energies of the excited states m are practically the same as the ground state since and. The excited states are semi-stable because N particles must be redistributed when going from an excited state m to the ground state 0. The natural decay times are measured in days.

Let us introduce boson field operators and which satisfy the Bose commutation rules:

(38)

where and is Dirac’s delta-function.

We take a system characterized by many-boson Hamiltonian H:

(39)

where is a single-boson Hamiltonian and is a pair potential energy. The field equation obtained from the Heisenberg equation of motion is

. (40)

We note that the field equation is nonlinear in the presence of a pair potential.

We can exprress and by

, (41)

where and are boson operators and and represent vacuum state vectors satisfying

. (42)

In the Heisenberg picture (HP) the boson states are time-independent and boson operators and move following the field Equation (40).

The single particle Hamiltonian h contains the kinetic energy, which depends on the momentum p only, and the boson-condensation Hamiltonian h_e which arises from the phonon exchange attraction. The ground state wave function is flat as seen from Equation (30). There are no gradients and no material currents. Hence, we obtain

, (43)

where the superscript (0) means the ground state average.

The ground-state energy of the pairon is negative and is given by w₀ in Equation (18). Hence we may choose

. (44)

The pairon has charge magnitude 2e and a size. For Pb the pairon linear size is about 10³ Å. Because of the Colomb repulsion and Pauli’s exclusion principle two pairons repel each other at short distances. We may represent this repulsion by a point-like pair potential:

. (45)

Using this and the random phase (factorization) approximation we obtain

(46)

Gathering the results (43), (44) and (46), we obtain

(47)

For the steady state the time derivative vanishes, yielding

. (48)

This is precicely, the GL equation, Equation (3) with and.

In our derivation we assumed that pairons move as bosons, which is essential. Bosonic pairons can multiply occupy the condensed momentum state while fermionic superelectrons cannot. The correct density condition (6) instead of (5) must therefore be used.

4. Discussion

We derived the GL equation from first principles. In the derivation we found that the particles that are described by the GL wave function must be bosons. We take the view that represents the bosonically condensed pairons. This explains the quantum nature of the GL wave function.

The nonlinearity of the GL equation arises from the point-like repulsive inter-pairon interaction. In 1950 when Ginzburg and Landau published their work, the Cooper pair (pairon) was not known. They simply assumed the superelectron model.

Our microscopic derivation allows us to interpret the expansion parameters as follows. The represents the pairon condensation energy, and the repulsive interaction strength:

. (49)

BCS showed [4] that the ground-state energy W for the BCS system is

, (50)

where is the density of states per spin at the Fermi energy and the pairon ground-state energy. Hence we obtain Equation (44): at.

In the original work [1] GL considered a superconductor in the vicinity of the critical temperature T_c, where is small. Gorkov [9] -[11] used Green’s functions and interrelated the GL and the BCS theory near T_c. We derived the original GL equation by examining the superconductor at 0 K from the condensed pairons point of view. The transport property of a superconductor below T_c is dominated by the Bose-condensed pairons. Since there is no distribution, the qualitative property of the condensed pairons cannot change with temperature. The pairon size (the minimum of the coherence length derivable directly from the GL equation) naturally exists. There is only one supercondensate whose behavior is similar for all temperatures below T_c; only the density of condensed pairons can change. Thus, there is a quantum nonlinear equation (48) for valid for all temperateures below T_c. The pairon energy spectrum below T_c has a discrete ground-state energy, which is separated from the energy continuum of moving pairons [5] . Inspection of the pairon energy spectrum with a gap suggests that

. (51)

Solving Equation (48) with Equation (6), we obtain

, (52)

indicating that the condensed density is proportional to the pairon energy gap.

We now consider an ellipsoidal macroscopic sample of a type I superconductor below T_c subject to a weak magnetic field H applied along its major axis. Because of the Meissner effect, the magnetic fluxes are expelled

from the body, and the magnetic energy is higher by in the super state than in the normal state. If the

field is sufficiently raised, the sample reverts to the normal state at a critical field H_c, which can be computed in terms of the free-energy expression (1) with the magnetic field included. We obtain after using Equations (6) and (50)

, (53)

indicating that the measurements of H_c give the T-dependent approximately. The field-induced transition corresponds to the evaporation of condensed paions, and not to their break-up into electrons. Moving pairons by construction have negative energies while quasi electrons have positive energies. Thus, the moving pairons are more numerous at the lowest temperatures, and they are dominant elementary excitations. Since the contribution of the moving pairons was neglected in the above calculation, Equation (51) contains approximation, see below.

We stress that the pairon energy gap is distinct from the BCS energy gap Δ, which is the solution of

. (54)

In the presence of a supercondensate the energy-momentum relation for an unpaired (quasi) electron changes:

. (55)

Since the density of condensed pairons changes with the temperature T, the gap Δ is T-dependent and is determined from Equation (54) (originated in the BCS energy gap equation). Two unpaired electrons can be bound by the phonon-exchange attraction to form a moving pairon whose energy is given by

, (56)

. (57)

Note that is T-dependent since Δ is. At T_c, Δ = 0 and the lower band edge is equal to the pairon ground-state energy w₀. We may then write

. (58)

We call the pairon energy gap. The two gaps have similar T-behavior; they are zero at T_c and they both grow monotonically as temperature is lowered. The rhs of Equation (54) is a function of; T_c is a regular point such that a small variation generates a small variation in Δ². Hence we obtain

. (59)

Using similar arguments we get from Equations (57)-(59)

. (60)

As noted earlier, moving pairons have finite (zero) energy gaps in the super (normal) states, which makes Equation (53) approximate. But the gaps disappear at T_c, and hence the linear-in- behavior should hold for the critical field H_c:

, (61)

which is supported by experimental data. Tunneling and photo absorption data [12] -[16] appear to support the linear law in Equation (60).

In the original GL theory [1] , the following signs and T-dependence of the expansion parameters near T_c were assumed and tested:

, (62)

all of which are reestablished by our microscopic calculations.

5. Conclusions

In summary we reached a significant conclusion that the GL equation is valid for all temperatures below T_c. The most important results in the GL theory include GL’s introduction of a coherent length [1] and Abrikosov’s prediction of a vortex structure [17] , both concepts holding not only near T_c but for all temperatures below T_c.

In the present work the time evolution of the system is described through the field equation for the boson operators and. The resulting equation

(63)

may be useful in deriving the Josephson-Feynman equation and describing dynamical Josephson effect [18] [19] . Operators u and are non-Hermitean, see Equation (35). Hence, a off-diagonal long range order simply arises from the definition of.

GL treated the effect of the magnetic field applied based on the super electron model. We shall treat this effect based on the moving pairons model separately.

Cite this paper

ShigejiFujita,AkiraSuzuki, (2014) Quantum Statistical Derivation of a Ginzburg-Landau Equation. Journal of Modern Physics,05,1560-1568. doi: 10.4236/jmp.2014.516157

References