Journal of Modern Physics
Vol.5 No.8(2014), Article
ID:46120,12
pages
DOI:10.4236/jmp.2014.58068
Hidden Dimensions Hypotheses
Piero Calcagno
Department of Electronics and Telecommunications, Politecnico di Torino, Turin, Italy
Email: calcagno.piero@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 30 March 2014; revised 28 April 2014; accepted 15 May 2014
ABSTRACT
Galileo introduced the scientific method, based on observation of natural phenomena, their interpretation and validation on the base of verified results. Albert Einstein broke the pattern of Galilean physics by postulating the invariance of the light speed and arguing that the laws of physics are valid independently of the inertial reference system used, introducing the concept of relativity and proposing a new physics based on four dimensions instead of the three previously known, with the addition of the variable time as the fourth dimension. In this article, we wonder if it is possible to find a methodology, necessarily not conventional, allowing to recognize additional new dimensions. The analysis of the quantization of nature has led us to hypothesize the use of irrational numbers in a ratio as a detector for any new dimension. A series of conjectures can bring us to imagine a scenario following the Big Bang with the creation of orthogonal matter, allowing us to find a seemingly plausible explanation to some unanswered questions of the contemporaneous physics. Under these hypotheses, it is possible to give two not conventional interpretations about gravity and light. The article prefers the logic explanation of the phenomena to their quantification through mathematics, reserving this last one only where it is necessary to clear the concept.
Keywords:Astrophysics, General Relativity, Many-Worlds Interpretation, Orthogonality, Physics

1. Introduction
Galileo Galilei (1564-1642) began the modern science observing the phenomenon of the tides. He and his contemporary Kepler, though arriving at different conclusions, used both the observation and prediction method to explain physical events. After Archimedes of Syracuse (c. 287 BC - c. 212 BC), Galileo was probably the first scientist that introduced the scientific method founded on the rigorous observation of facts and on their experimental validation, separating them from philosophy and religion, causing a great development of human thought. His opera was very extensive and rich. He asserted that the nature laws are based on mathematics [1] . Albert Einstein (1879-1955) called Galileo the “father of modern physics” [2] . In this article, I present a not conventional methodology to help in detecting hidden dimensions formulating a few conjectures. The world that we know has three dimensions, and in the last century, further time-dimension has been added. In the Galilean space, the distance between two events is an absolute value not depending by the observer’s reference system, while the space-time in the restricted relativity both these values become relative and depend by the observer’s reference system. Nevertheless in the restricted relativity under the postulate of the invariance of the light speed c, in a given coordinate system (χ µ) exists a distance d between two events (tA, xA, yA, zA) and (tB, xB, yB, zB) independent by reference, not modified by the Lorentz’s transformation, given by:
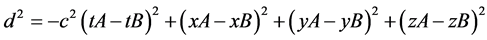 (1)
(1)
Each of the four terms of the addition is relative to a single dimension of a (t, x, y, z) space defined as also space-time. There are other mathematical formalisms useful to describe the distance between two events but now we stop at the relation (1) that, as extension of the last Fermat theorem, assures real solutions.
2. Irrational Numbers
The irrational number is any real number which is never equivalent to a fraction 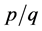 for any integer p and q (q ≠ 0). The irrational number has an infinite decimal expansion without become periodic. This is a mathematical definition. Until now we have found many irrational numbers; theory affirms they are infinite.
for any integer p and q (q ≠ 0). The irrational number has an infinite decimal expansion without become periodic. This is a mathematical definition. Until now we have found many irrational numbers; theory affirms they are infinite. 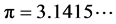 known as Archimedes constant is the ratio of any circle’s circumference to its diameter; π is a pure number, in other words it is independent of measure unit used and it is also a transcendental number. To describe the diameter we need a single Cartesian axis or dimension, to describe a circumference we need two axes and its measure will be π times the measure of the diameter. Another irrational number is
known as Archimedes constant is the ratio of any circle’s circumference to its diameter; π is a pure number, in other words it is independent of measure unit used and it is also a transcendental number. To describe the diameter we need a single Cartesian axis or dimension, to describe a circumference we need two axes and its measure will be π times the measure of the diameter. Another irrational number is  Also in this case the
Also in this case the  is the ratio between the diagonal d and the side l of a square. To describe a side we need a single dimension, to describe a diagonal starting by a side we need two dimensions. In the case of the cube, the value of diagonal is given by:
is the ratio between the diagonal d and the side l of a square. To describe a side we need a single dimension, to describe a diagonal starting by a side we need two dimensions. In the case of the cube, the value of diagonal is given by:
 (2)
(2)
We use the same dimensional unit for both greatness in the (2), but not it is possible use the same elementary tile to permit to quantize both greatness as different multiply of the same elementary tile. Following these considerations, we can affirm that, in a granular world, an irrational pure number can be considered a ratio putting in relation a single dimension with another-one belonging at the same space. Defined a conjecture as an unproven proposition, which we believe to be true and never been disproved, we can show this conjecture (in the following text the conjectures are numbered as (C1), (C2)··· while the relations are numbered as (1), (2)···):
An irrational pure number in a relation, tying two physical quantities, is a detector of two or more adjacent dimensions. (C1)
As we will see in the next paragraphs, at different dimensions we can attribute the property of orthogonality. So the (C1) can be written as follow:
If we meet an irrational pure number tying two physical quantities, these are of the same nature, belong to the same space, and are positioned over two o more different orthogonal dimensions. (C2)
Extending the (C2) we have:
If we found an irrational dimensioned number tying two physical quantities, these are not of the same nature, belong at the same space and are positioned over two or more different orthogonal dimensions. (C3)
We consider the speed of the light in the vacuum c. The postulate of Einstein on the restricted relativity affirm that c is invariant in a coordinates system (χ μ) and for this feature, also let see the conjecture (C7) in the next paragraphs, it is an up limit for any speeds of kind of particles. For these considerations we can postulate:
The speed of the light in the vacuum is an irrational dimensioned number. (C4)
Then we can verify that the relation:
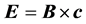 (3)
(3)
where E is the electric field vector, B is the magnetic field vector, c the speed of the light vector, the (3) can be a necessary, but not sufficient, validation satisfying the (C3), the (C4), and the (C7). If the conjectures (C2) and (C3) will verify true, we will be able to use a new operator to recognize new dimensions.
3. Introduction at the Orthogonality
If we cannot enter with our senses in an n-dimensional space with n > 4, we can imagine to live in a mono-dimensional world (n = 1) and start from this more simple world to think to find a more complex space (n ≥ 2) with the possibility to verify if our hypothesis is true. If we can find mathematical operators able to introduce ourselves in this other space, in a verifiable way because we know already the answer, we can propose a conjecture, in order to extend these operators, these properties, to an n-dimensional space. In a mono-dimensional world we can move ourselves along a curve-line in both available directions, on an infinitely long path. This path can be rectilinear or, more probable, curved. At every movement we can change our coordinate of one, two, … a thousand values.
If we change the value unit reducing it at one half, or at another value, the distance covered will be reduced of one half, or of the other value. I ask if there a room not accessible at our stride. If the conjecture (C1) about irrational number is true, we cannot go over any point positioned at one irrational distance from the start. We can go in an infinite number of places to pose our feet, which are the set of rational numbers, but cannot go to pose our feet on an irrational number. In fact we can go extremely near to the irrational point but that point will be inaccessible to us. We have discovered that there is a limit, a regular granularity [3] at our advancing, that we can not violate. The world, also that small mono-dimensional world apparently linear and continuous, in the extremely small is discontinuous, exactly like in the elementary particles of the atomic world. The same definition of atom (atòmos in Greek) to date from Democritus, Epicurus and Leucippus describes the smallest indivisible particle of matter. In more recent time, in 1900, Max Planck (1858-1947) supposed and demonstrated that the energy E of a wave can transport is in a packet format: one, two,··· a thousand of packets following the relation:
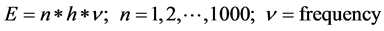 (4)
(4)
where h = 6.62606896 ´ 10(‒34) J×s is the Planck’s constant. Energy with a value not correspondent to an integer number of packets does not exist; Energy value of 3.73 packets does not exist: or are 3 packets or 4 packets; any value measured of Energy must be a multiply of h. By relations (4) and (6) we get h ´ ν = m ´ c² known as Compton scattering began the debate on duality wave-particle. Therefore for the equivalence mass-Energy, we can affirm that also the mass has a minimum value of elementary step: one for every kind of particle we are considering. We can say, at least under this point view of that mono-dimensional world and the real world, that we can test and verify are similar: they are granulate worlds. In this countable mono-dimensional frame, we imagine that a mathematician make us discover the number π (3.141592···). What is the relation of this number with us mono-dimensional subjects? We don’t understand this number, we cannot measure it in our world, but if we look at the boundary of our world and of our thought, we can perceive our limit. In fact supposing that our mono-dimensional world is rectilinear, the distance of a segment d, π time d is exactly the distance that we should cover walking a circle using two coordinates relative at two axes, two dimensions. We learn the existence of another dimension, even if we live in a single dimension and we cannot cover a circle. We have found a confirmation of the conjecture (C1).
Another way to describe this phenomenon: if two wayfarers A and B start to move from the same point O in two orthogonal directions. The two wayfarers live both in two mono-dimensional worlds, but these worlds have a common point in O, that is their only meeting point or cross point. The steps are like a linear tiled floor having an only single tile in common, the O tile. A and B go on in synchronized way tide by tide. After a time chosen at pleasure, the distance (the same quantity d of the (1)) between A and B shall be always  their distance (in tile) by the point O. Reading the distance at the same time for the two synchronized wayfarers, the time in the (1) is annulled. The irrational number starting by mono-dimensional world, one ∞ degrees of freedom, detects a two-dimensional world: a surface, more complex by two curve-lines, one ∞² degrees of freedom. A and B, in order to meet directly following the geodetic line, must enter in a more complex world: a surface.
their distance (in tile) by the point O. Reading the distance at the same time for the two synchronized wayfarers, the time in the (1) is annulled. The irrational number starting by mono-dimensional world, one ∞ degrees of freedom, detects a two-dimensional world: a surface, more complex by two curve-lines, one ∞² degrees of freedom. A and B, in order to meet directly following the geodetic line, must enter in a more complex world: a surface.
4. Orthogonality
We can define orthogonality if the projection of one dimension upon second-one is only in one point. This means that if a wayfarer moves in one dimension, in the other dimension he stands still. We can enunciate a conjecture:
If two orthogonal quantities exist, they indicate two dimensions. (C5)
The three Cartesian dimensions detect a 3D space, known at our senses, but also the electric field, the magnetic field and the electrodynamic force applied to a mobile conductor passed through electric current, immersed in a magnetic field, are examples of orthogonality, and if the conjecture (C5) is true, they belong to different dimensions. We know and can validate the space-time world described by (1), but there is also other orthogonal worlds partially or completely not known. If we would live in a mono-dimensional world, it would be difficult to think about a world upon a surface. How is possible to know the properties of a dimension not accessible to us? To answer at this question we can use the hypothesis of analogy.
Similar properties in different dimensions, apparently without relations between themselves, correspond similar relations and vice versa. (C6)
Written in other way: if we understand the properties of the universe in one of its parts, we can extend our knowledge to the parts not immediately accessible to us, but with similar properties. There are many examples where (C6) works. For the law of conservation of energy, or also for the Noether’s theorem, a moving body tends to conserve his movement indefinitely. If we inject a current in a coil and this coil can change its geometry, the coil will get the geometry that will let it not to change the magnetic flux. We can affirm, that motion and magnetic flux are equivalent. A further propriety of the orthogonal dimensions is the following:
When a dimension crosses another-one in a point, the shown properties are always constant and invariable; this characteristic is independent from the cross point and has null entropy. (C7)
The property of null entropy in the cross point of the (C7) is obtained by the application of the Fluctuation theorem [4] relative to the only hidden dimension in the cross point. From the point of view of our dimension, we are far from thermodynamic balance, while the other dimension appears constant and invariable. This property is interesting for further important considerations, not only in this article, but also for its applications in the cellular world [5] .
5. A new Interpretation of the Gravity
The gravitational field has laws equivalent to electric and magnetic fields, but it has a peculiarity: it is monodirectional. For this reason, it was not possible to insert the gravity in the Standard Model and only the String Theory permitted a more complete description of the universe. There are many new important proposals coherent with the general relativity (GR) going further trying to solve problems like the non-renormalization [6] [7] . This article is not full of precise relations but tries to indicate new ways of investigation. We have seen that two orthogonal quantities cannot integrate together and require a new dimension: two dimensions. Every quantity won’t visible, not accessible at the other-one; they will meet only in the interception point, in the common point. If our mass, our world, is intrinsically immerse in a second mass, in a second world orthogonal to our world, or in more extensive way, in many other worlds all orthogonal to the others, we do not realize their presence. Our world occupying the available space, would receive a push like to a body immersed in a liquid which is pushed with a value equal to the mass of the moved liquid. The gravity could be this push: a generalization of the Archimedes principle. We should be asking our-self what is the equivalent of the liquid moved: if the orthogonal mass or the real: I should inclined the second-one is the right. In any case:
The gravity would not be an intrinsic force, a new force [8] , it would be an effect of the simple allocation of the mass in the universe, and the impediment to occupy the same space to other orthogonal masses. (C8)
In the gravity the absence of polarity is explained with the (C8) conjecture, because the absence of free space between masses pushes them to com-penetrate in mono-directional way. We can call this phenomenon “osmotic pressure of the universe” comparing this behavior to a container full of water divided by a membrane in two sections, where in one of them is poured a small quantity of NaCl. After a not definite time, the membrane curves inside the part without salt. In fact the salt tends to occupy uniformly all the water. I ask myself, without giving me an efficient answer about that, what is the difference between my interpretation of the gravity and the Higgs field. The gravity acts immediately: in the case of long distances it violates the limit of speed of the light in the vacuum. An interpretation of this peculiarity are the conjectures (C7) and (C8) validating them. Ideally if we have many balls everyone touching the others, with contacts points aligned along a straight line, and we give a pulse at one extremity of these series of balls, the last ball on the other side of the series receives immediately the same pulse. The balls are the orthogonal matter. We note that also in our world, the Archimedes principle is applied without entropy independently by the viscosity of the liquid where the mass is immersed. If the conjecture (C8) is valid this means that:
Our universe is not quite empty of visible matter, but it is full of orthogonal matter. (C9)
In 2004 a group of scientists [9] proposed a conjecture similar to (C9) searching an interpretation of the universe without the Higgs boson. A universe full of orthogonal matter can explicate how light can propagate in the sidereal empty space and how it isn’t possible to detect the James Maxwell’s beloved old ether. These orthogonal worlds can clear up because the dark matter and the dark energy have been perceived but not found in our universe. If this reasoning is right we would have found a way to perceive orthogonal worlds next to ours. The two fundamental postulates of Albert Einstein which permitted the Theory of the Relativity, are the invariance of the speed of light c in the vacuum and of the physic’s laws in any inertial system. We could find an explanation for these postulates with the conjecture (C7) casting the light and the physic’s laws as realities are belonging to orthogonal worlds to ours and have in common with ours only the cross point and for this reason they have always the same value in any reference system known to us. By:
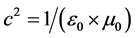 (5)
(5)
with ε0, μ0 dielectric and magnetic constant in the vacuum, we found that these quantities belong to the same space and are orthogonal to each other. An interesting consideration is that the space occupied by matter in one dimension subtracts the same space to another matter living in another orthogonal dimension that in any case, tends to full fill the empty room. This tension can explain also the forces keeping together a body, without losing its small components, or also other effects like the Casimir one. We know that our universe is finite and in expansion [10] [11] , that the cosmic microwave background radiation (CMB) is steady at a temperature of 2.725 K [12] and that the density of matter remains constant [13] -[16] . In our universe the matter of stars generates energy, but by the Einstein’s relation [17] :
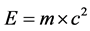 (6)
(6)
We must admit that the ratio E/m is one constant; this means, that if the global energy in the system increase, also the mass must increase. The hypothesis of this article is, that new matter is generated in orthogonal dimensions. In a later section I will try to highlight this statement mathematically. This should explain the constancy of cosmic radiation CMB and the density of matter through the diffusion in the universe and permits the validity of the (C8) in time. This should explain also the isotropy and the flatness of the visible matter in the universe.
6. Considerations about Light
A possible validation of the (C9) is a new interpretation of the proves of the general relativity (GR), beginning with a new interpretation of light deflection near a strong gravitational field [18] . Let’s start with an introduction. The light has an orthogonal nature if seen for its respect to the angle of incidence with the material. In fact, in the refraction phenomena is valid the Snell’s law:
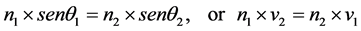 (7)
(7)
n1, v1 and n2, v2 are the refraction indexes, namely the characteristics of the medium that the light passes through and the relative crossing speed; senθ1 and senθ2 are the geometric characteristics with respect to the perpendicular to the plane of incidence. This law is valid in every known space-time, in other words it doesn’t depend by the geometrical position not by the reference system used. In case of perfect perpendicularity, refraction and reflection of light doesn’t happen. Light changes its speed passing though materials of different transparency or different refractive indexes, but its trajectory doesn’t change. Therefore there are no entropy phenomena or phenomena of exchange between different types of energy. The only place known in our space-time with null entropy is at the boundary of our space-time as the (C7) explains. In the same way, gravity has an orthogonal nature over a surface. Let’s think to the forces applied to a mass on an inclined plane. Also in this case, the activated force is modulated by senθ with θ angle of inclination of the inclined plane. In the case of the gravity, we can verify the phenomenon only if we use the gravitational field that we have available, that is the one referred to the horizontal plane because we are immersed in a gravitational field. After this introduction we can affirm what follows:
The light that we perceive arrives from an orthogonal direction respect at our space-time. (C10)
Moreover we have:
Light and gravity are similar and are orthogonal at our space-time. (C11)
When light cross different transparent materials with different index of refraction, it is similar to a ball rolling over an inclined plane with different slopes. The difference is that the light has zero mass: for this reason aceleration or deceleration at the point of change are infinite. The consideration (C11) is similar to that theory of strings saying: “the graviton should be without mass and charge and must have spin two” [19] . So the (C11) coupled to (C9) and the consideration that the orthogonal mass is located outside the actual mass as assumed by (C8), suppose a concentration of orthogonal mass around the big masses of the real universe. It is possible that this concentration comes distributed as the conjecture (C12) says:
The increase of the distribution of the orthogonal matter all around at the m real mass assumes the form of an all around spherical cap of equivalent molar volume m of the real mass. This concentration decreases in quadratic form moving away from the real mass. (C12)
The increase of orthogonal mass results:
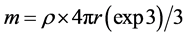 (8)
(8)
The law operating in the refraction in the orthogonal space should be the Lorentz Lorentz formulation called molar refractio
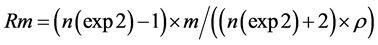 (9)
(9)
This formulation is updated [20] only in function of the water and its vapor in the range 182 nm ≤ λ ≤ 2770 nm in the temperature range −10˚C ≤ T ≤ 500˚C and in density 0.0028 kg/m (exp3) ≤ ρ ≤ 1045 kg/m (exp3). It is clear that this formulation shall be extended at range more extensive and the simplification given by ratio m/ρ by (8) applied only in case of uniform distribution is not valid. If the (C7) is validated, the light of a star should arrive to us going though the orthogonal space following the law of refraction to present itself to our observation with its characteristics of independence and constancy by each system of reference. In short, only when we observe the light, it goes from orthogonal space to ours. As all we see, we detect it in the same way, and for the (C10) it has being orthogonal in this transition does not changed the path, we do not perceive the changing of the speed of the light crossing from a velocity c0 (speed of the light in the deep orthogonal space, without a near mass disturbing) to speed c (speed of the light in the vacuum of the space-time).
In the case the light transits near a real mass, then it is valid the (C8), the density of the orthogonal matter increases (simplifying with no-continue values n0 < n1 < n2 < n3 as shown in Figure 1) with correspondent reduction of the speed of the light (c3 < c < c < c0) with a small deviation around the mass following the Snell’s law in the orthogonal space and in output from the influence of the mass with a gradual return at the c0. Known the real mass and then the medium orthogonal mass around the real mass (planet), we shall found the index of refraction n0. If n0 shall be smaller than n, index referred to our space-time, the speed of the light in orthogonal space shall be greater of c given by the (5). The consequence should be a revision of the amplitude and of the time of life of our universe known until now. If the line of reasoning done is correct and in particular is correct the conjecture (C10), we should think that the light exists in a bi-dimensional space ξ revealed by the E and B vectors by (3) those intersect in orthogonal way our space-time μ simplified at only 2-dimensions (μ plane in Figure 2).
What we see and we can measure of light, is not the whole but only its intersection with our space-time. This explains the reason why we can’t see a ray of light in a vacuum, while we can see it if there are more particles on its path belonging to our world (μ plane) operating as a reflecting detector. Then it is very interesting to try to
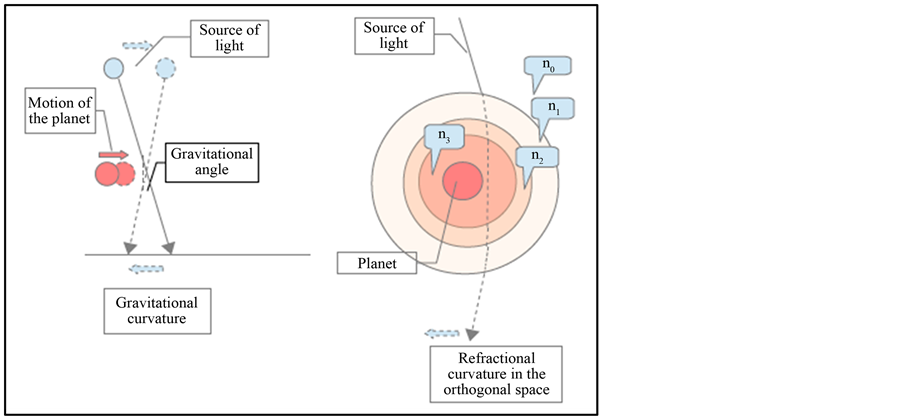
Figure 1. In the orthogonal space, refractional curvature of the light, when it is near a big real mass.
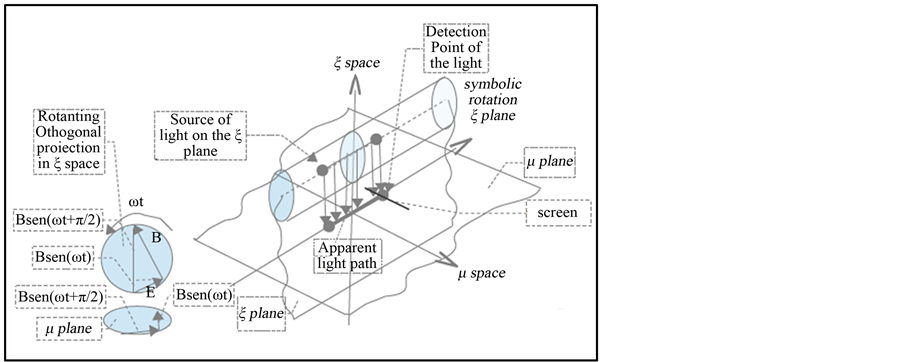
Figure 2. The light exists in the ξ space and comes detected in μ space only when meets particles belonging at μ space. ξ space and μ space are mutually rotating.
understand the behavior of light when it passes through a single slit or a double slit in our space-time. What we see on the screen (simplified at one-dimension only in Figure 2) is the projection of the vectors E and B on the ξ plane and the further their projection on the μ plane. If the ξ space is rotating at ωt speed respect at ξ plane jointly and severally to the orthogonal μ space-time, we shall see on the screen the interference fringes in the double slit experiment. In Figure 2, the rotation of the ξ space comes represented in symbolic way and it generates two orthogonal vectors of value 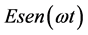 and
and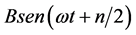 . For this reason the nature of light appears to us as a wave. In reality, each photon belongs to a single space not related to ours. In fact, each photon has its relative frequency of rotation with respect to our world and so you can imagine that photons of different frequencies exist in spaces with different relative speed of revolution with respect to our space-time. The randomness [21] , which intervenes in the behavior of the particles, is due to the rotation of the space ξ of existence of the same in respect of our μ observation space-time.
. For this reason the nature of light appears to us as a wave. In reality, each photon belongs to a single space not related to ours. In fact, each photon has its relative frequency of rotation with respect to our world and so you can imagine that photons of different frequencies exist in spaces with different relative speed of revolution with respect to our space-time. The randomness [21] , which intervenes in the behavior of the particles, is due to the rotation of the space ξ of existence of the same in respect of our μ observation space-time.
To continue with the explanation of the effect of drag (or frame dragging [22] ), we must consider the effect of the pressure of the rotating orthogonal matter on our space-time. If the path of light is coherent with the rotational movement of the mass grazed by the ray of light, as the light is crossing the orthogonal at real mass but is coherent with its movement, it increases the real speed because the ray of light encounters less orthogonal mass on its path; otherwise if the light passes in the proximity of an object with a rotating mass in the opposite direction of the mass, the speed will be reduced because it meets more matter. The same explanation is valid for the Doppler Effect. We learned how to use the concept of orthogonal matter and how it works.
In a similar way, we can understand the refraction of light in a prism. If the frequency of light is greater, this means the revolutions of the ξ space are more, and more is the friction, without entropy, with orthogonal space, and more evident will be the deviation of the ray of light.
If all these hypotheses result true, we should consider at least two kinds of orthogonal matter, not necessarily belonging to the same space and therefore not necessarily in communication one with the other. The orthogonal gravitational space, that we could call field of Higgs or texture of the universe, is responsible of the gravity of the masses in our universe as by (C8), and it is orthogonal both with respect to our space-time and to the one creating orthogonal material to compensate the decrease of the material in the star reactions. This second space, as (C13) shows, exerts pressure on the spaces above and, taking advantage of the small initial anisotropy after the BIG BANG, it is the one responsible of isotropy and of the flatness of our universe. The behavior of light hypothesized in this article results equivalent to the relativistic theory and can permit to go up to the density of orthogonal matter around the mass simulating the relativistic curvature of the space-time, that is confirmed by experimental [23] and theoretic [24] results.
7. Hypothesis of Energy and Mass Existing Also in an Orthogonal Space
Considering the (6), the equivalence mass-Energy, the constancy of the ratio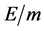 , if the conjecture (C4) results true that is an irrational dimensioned ratio, than E and m belong two different dimensions.
, if the conjecture (C4) results true that is an irrational dimensioned ratio, than E and m belong two different dimensions.
There is analogy with the relation tying the diagonal d of a square and the length l of its late
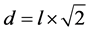 . (10)
. (10)
Using the (C6), m can take as real value (equivalent to l of the (10)) coherent with our world tied to values as volume and specific gravity, E is the measure of the hypotenuse (equivalent to d in the (10)) relative to a right triangle having as other cathetus the Energy orthogonal to the mass.
If in the space μ where m and E are belonging, a nuclear transformation generates a small decrement of mass ‒Δm, a quantity of energy +ΔE will generate given by:
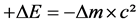 (11)
(11)
but if E increase and m decrease, the ratio E/m doesn’t keep constant in μ at least considering μ as an isolated system. The interpretation of this phenomenon in this article is given in this way: I introduce a conjecture:
E and m´c² exist not only in the μ space but also in the ξ orthogonal space. (C13)
Together the (C13) is valid also the Conservation Energy Principle to booth spaces. E represents the energy assigned to space μ and Eξ that assigned to space ξ in the Big Bang. Than if: ![]() and
and ![]()
Than the (6), as shown in Figure 3, becomes:
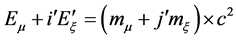 (12)
(12)
where
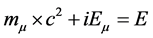 (13)
(13)
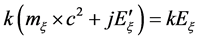 (14)
(14)
with i = j = k are the operators of the imaginary unit rotating of 90˚ the vector in the relative plane of reference with k × j = i' e k = j'. Accepting the first dimension mμ real, since the dimensions are four and the imaginary operators are three (i, j, k).
From the (13) and (14) we have:
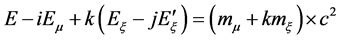 (15)
(15)
If after a nuclear fission or other reduction phenomenon, from the (15), we will have in the space μ: mμ becomes mμ − Δmμ, with reduction of the mass, Eμ increases becoming Eμ + ΔEμ, following the (11), leaving E unchanged as shown in Figure 4, that is also a representation of the (1) when the dimensions are two. Reassuming, after a nuclear transformation in the space μ we will have:
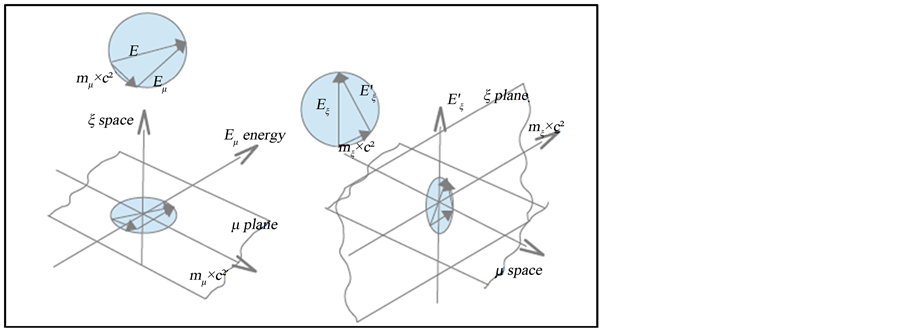
Figure 3. m and E exist in μ space and in the orthogonal ξ space.
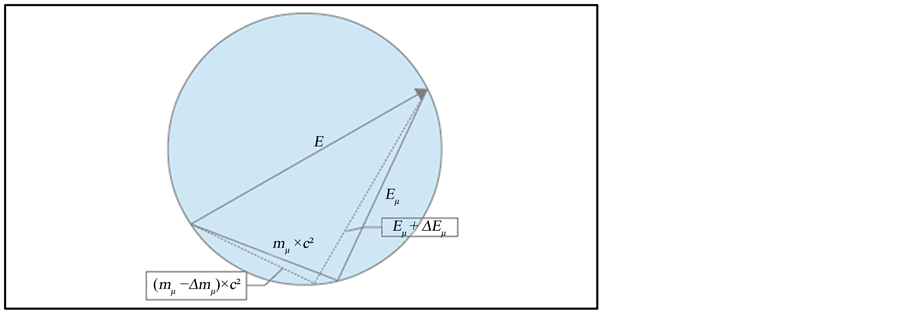
Figure 4. In μ space a reduction of the mass and the correspondent increase of the Energy don’t change the ratio E/m if the ξ space exists.
![]() and
and ![]() with E not variable as shows in Figure 4.
with E not variable as shows in Figure 4.
Moreover in the space ξ they are the following variations:
![]() and
and ![]() with Eξ unchanged.
with Eξ unchanged.
This four variations recognize the extremes of a cycle like that thermodynamic interesting both μ and ξ spaces. For the Conservation Energy and Mass Principle we have:
![]() and
and ![]() In practice happens a transfer of mass from space μ to space ξ compensated by a transfer of energy from space ξ to space μ as shown in Figure 5. Both bi-dimensional space μ and ξ are represented in Figure 5 for simplicity over Cartesian coordinates and are to interpreter as their orthogonal projection on the sheet.
In practice happens a transfer of mass from space μ to space ξ compensated by a transfer of energy from space ξ to space μ as shown in Figure 5. Both bi-dimensional space μ and ξ are represented in Figure 5 for simplicity over Cartesian coordinates and are to interpreter as their orthogonal projection on the sheet.
The effect of all variations Δ of the quantities applied to (6) and then to (15) keeps constant the modulus of the ratio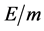 . The entropy of the space μ tends to increase, while that-one of the space ξ tends to decrease. If exist a boundary between two spaces, in that boundary the entropy will be null satisfying the Fluctuation Theorem. The (11) is only an indicative relation useful to make clear the sign and the sense of the variations. To try to validate the conjecture (C13), if we would valuate better the increase of the energy
. The entropy of the space μ tends to increase, while that-one of the space ξ tends to decrease. If exist a boundary between two spaces, in that boundary the entropy will be null satisfying the Fluctuation Theorem. The (11) is only an indicative relation useful to make clear the sign and the sense of the variations. To try to validate the conjecture (C13), if we would valuate better the increase of the energy ![]() corresponding at a decrease of mass
corresponding at a decrease of mass ![]() from Figure 4, we can proceed in this way:
from Figure 4, we can proceed in this way:
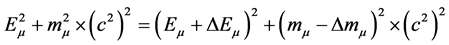 (16)
(16)
and then:
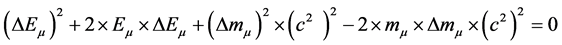 (17)
(17)

Figure 5. As a small variation of the mass in μ space changes Energy and mass in ξ space.
from which, one of two solutions is:
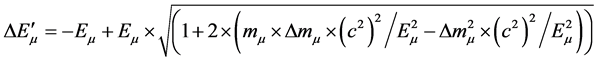 (18)
(18)
The exact relation, we are searching for, is the (18).
We can found an approximation disregarding the term  respect at term
respect at term ![]() remembering the (6) we have:
remembering the (6) we have:
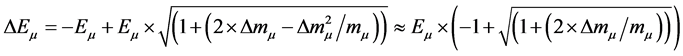
Applying the development in series of MacLaurin, and approximating at only the first and second terms of the series, we obtain:
 (19)
(19)
The (19), corresponding at a positive term of the (16), is an increase of the energy produced in the μ space.
We can ask ourselves the meaning of the second solution (20) of the equation (17), and what physical meaning it has.
 (20)
(20)
that working in the same previous way, gives the approximate value:
![]() (21)
(21)
The hypothesis is that this subtraction of energy by μ space moves to ξ space to create the orthogonal mass ![]() left a decrement of the orthogonal energy
left a decrement of the orthogonal energy ![]() as shown in Figure 5. We can repeat the same procedure in the orthogonal ξ space. It is clear with reference to Figure 3 E and Eξ are dual but not necessary of equal value, nevertheless we will see, for the stability of the system these values are equal. The (16) is dual of the (22):
as shown in Figure 5. We can repeat the same procedure in the orthogonal ξ space. It is clear with reference to Figure 3 E and Eξ are dual but not necessary of equal value, nevertheless we will see, for the stability of the system these values are equal. The (16) is dual of the (22):
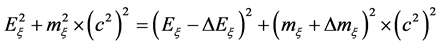 (22)
(22)
This equation admits the two solutions (23) and (24):
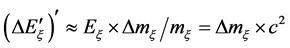 (23)
(23)
The (20) is dual of the (19) nevertheless the (22) corresponds to a decrement of energy in the ξ space. The other solution (24) is dual to (21):
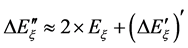 (24)
(24)
It is evident, that the first two solutions are represented by Figure 3, while the second-ones are real in the union of the two spaces μ and ξ but are of opposite sign and then they represent an instantaneous energetic exchange of great intensity between μ and ξ. Nevertheless the experience says the space-time μ continues to exist also after the lost of![]() . The explanation is that the system is in balance and the values are equal as by (25) realizing a particular symmetry like described previously and shown in Figure 5.
. The explanation is that the system is in balance and the values are equal as by (25) realizing a particular symmetry like described previously and shown in Figure 5.
![]() (25)
(25)


All these considerations seem to validate the conjecture (C13).
This architecture consents interesting variations. An example is the case where various masses belonging to spaces μ and μ', share the same orthogonal mass in the space ξ. This scenario could explain curious phenomena like quantum entanglement [25] and the Efimov effect. In both cases there is a remote action, apparently unexplainable between masses in μ and μ'. These considerations could become a contribution to the validation of the proposal of this article. In fact the interactions between orthogonal spaces can give visible effects in the spacetime open to very exciting scenarios and perspectives.
If c is the up limit for any universe speed, than since v = s/t, a minimum small little time will must exist; under that-one it is not possible go down. The expansion of the space after the Big Bang starts from that-one. The expansion in an orthogonal space generates the space-time that generates the gravity. If the conjecture (C8) is valid, the space-time distortion is the contraction of the orthogonal mass which is not able to enter in the real mass. If we follow the conjectures applied in this article, the space-time distortion is not stable. In fact, if the (C13) is a valid proposition, a star generates orthogonal matter with increasing of the space-time distortion with the increase of the time. It is strange because the mass of the star should decrease, before its collapse. This phenomenon, if it will be verified, could become a validation of the conjecture (C13).
8. Conclusion
Starting from the background and achievements from the history of science, we tried to find a methodology that allows a non-conventional thinking about how to highlight any dimension hidden to our senses. The observation of the present world which is granular and not continuous was essential. The variables belonging to hidden dimensions, but also known to our world, should live in their dimensions, where they enjoy a degree of freedom and have contact in the cross point in our world, sharing with us their specific properties in that point. We looked for operators acting as detectors between dimensions and can identify a further dimension. We identified these peculiarities in the pure and irrational numbers. Various conjectures have been introduced allowing us to describe different dimensions both of the same type and heterogeneous. This second case uses irrational, but not pure, numbers discovering different spaces. We explained the concept of orthogonality, which should be common to all dimensions, in order to fit in different spaces, each of them consisting of one or more dimensions. We introduced the concept of similar relation in different spaces, in case of similar properties. This article tries also to give an answer to the two postulates that were at the basis of the theory of relativity introducing the orthogonality in the dimensions. A new orthogonal space comes introduced, using the mass and the energy as dimensions, introducing a new interpretation of gravity. In the same way, a new explanation of the apparent wave nature of the light has been introduced, using another orthogonal space rotating respect at our space-time. Under these conjectures we can try to answer to few questions opened of the contemporaneous science.
References
- Stillman, D. (1957) Discoveries and Opinions of Galileo. Doubleday & Company, New York, 237-238.
- Einstein, A. (1954) Ideas and Opinions. Crown Publishers, New York.
- Wiener, N. (1966) Differential Space, Quantum Systems, and Prediction. The Massachusetts Institute of Technology Press, Cambridge.
- Evans, D.J. and Searles, D.J. (2002) Advances in Physics, 51, 1529-1585.
- Ana-Suncana, S. (2010) Nature Physics, 6, 726-729.
- Horava, P. (2009) Physical Review D, 79, Article ID: 084008.
- Mukohyama, S. (2010) Classical and Quantum Gravity, 27, Article ID: 223101.
- Verlinde, E. (2010) On the Origin of Gravity and the Laws of Newton.http://arxiv.org/PS_cache/arxiv/pdf/1001/1001.0785v1.pdf
- Csaki, C., Grojean, C., Murayama, H., Pilo, L. and Terning, G. (2004) Physical Review D, 69, Article ID: 055006.http://arxiv.org/pdf/hep-ph/0305237.pdf
- Peebles, P.J.E. and Ratra, B. (2002) The Cosmological Constant and Dark Energy.http://arxiv.org/PS_cache/astro-ph/pdf/0207/0207347v2.pdf
- Marinoni, C. and Buzzi, A. (2010) Nature, 468, 539-541.
- Penzias, A.A. and Wilson, R.W. (1965) Astrophysical Journal, 142, 419-421.
- Lemaitre, G. (1931) Monthly Notices of the Royal Astronomical Society, 91, 483-490.
- Connolly, A. (1995) Introductory Astrophysics—A113.http://www.phyast.pitt.edu/~ajc/teaching/chap26/chapter26.pdf
- Schutz, B. (2003) Gravity from the Ground up: An Introductory Guide to Gravity and General Relativity. Cambridge University Press, Cambridge, 361.
- Scott, D. (2005) The Standard Cosmological Model.
- Einstein, A. (1959) Il significato della relativita. Boringhieri, Torino, 45.
- Clifford, M.W. (2001) Living Reviews in Relativity, 4, 35-39.
- Greene, B. (2012) La realta nascosta. Einaudi, Torino, 104.
- Thormahlen, I., Straub, J. and Grigull, U. (1985) The Journal of Physical Chemistry, 14, 933-945.http://www.nist.gov/data/PDFfiles/jpcrd282.pdf
- Vaidman, L. (1996) On Schizophrenic Experiences of the Neutron or Why We Should Believe in the Many-Worlds Interpretation of Quantum Theory. http://arxiv.org/pdf/quant-ph/9609006.pdf
- Kannan, R. and Saha, P. (2009) IOP the Astrophysical Journal, 690, 1553-1557.
- Bertotti, B., Iess, L. and Tortora, P. (2003) Nature, 425, 374-376.
- Lewis, A. and Challinor, A. (2006) Physics Reports, 429, 1-65.
- Yao, X.-C., Wang, T.-X., Xu, P., Lu, H., Pan, G.-S., Bao, X.-H., Peng, C.-Z., Chen, Y.-A., Lu, C.-Y. and Pan, J.-W. (2012) Nature Photonics, 6, 225-228.

