Journal of Modern Physics
Vol.5 No.14(2014), Article
ID:49009,10
pages
DOI:10.4236/jmp.2014.514123
The Periodic Table of Elementary Particles Based on String Theory
Ding-Yu Chung
Utica, Michigan, USA
Email: dy_chung@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 March 2014; revised 26 April 2014; accepted 21 May 2014
ABSTRACT
In this paper, all elementary particles (leptons, quarks, gauge bosons, and the Higgs boson) can be placed in the periodic table of elementary particles based on string theory with oscillating spacetime dimension number, instead of conventional string theory with fixed space-time dimension number. Dimension number oscillates between 11D and 10D and between 10D and 4D reversibly. The oscillation of space-time dimension number (D) is accompanied by mass dimension number (d) to represent mass. Space-time dimension number decreases with increasing mass dimension number, decreasing speed of light and increasing rest mass. 4D particle originally is 4D10d particle, and has the lowest speed of light and the highest rest mass. With the same energy, the relation between adjacent mass dimensions is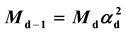 , where M is rest mass, d is mass dimension number, and α is the fine structure constant. According to the proposed cosmology, the non-gravitational 4D10d particles were sliced into 4D4d core particles surrounded by 6 separated mass dimensions as the 6 dimensional orbitals constituting the non-gravitational forces (electromagnetism, strong, and weak). The combination of the 6 dimensional orbitals and the gravitational 4D10d particle resulted in the 7 dimensional orbitals. As the periodic table of elements based on the atomic orbitals, the periodic table of elementary particles is based on the combination of the two asymmetrical sets of the 7 dimensional orbitals. One set as the principal dimensional orbitals is mainly for leptons and gauge bosons, and another set as the auxiliary orbitals is mainly for individual quarks. The calculated constituent masses of leptons, quarks, gauge bosons, and the Higgs boson are in good agreement with the observed values. For examples, the calculated mass of top quark is 176.5 GeV in good agreement with the observed 173.34 GeV, and the calculated average mass of the Higgs boson is 128.8 GeV in good agreements with the observed 125 or 126 GeV.
, where M is rest mass, d is mass dimension number, and α is the fine structure constant. According to the proposed cosmology, the non-gravitational 4D10d particles were sliced into 4D4d core particles surrounded by 6 separated mass dimensions as the 6 dimensional orbitals constituting the non-gravitational forces (electromagnetism, strong, and weak). The combination of the 6 dimensional orbitals and the gravitational 4D10d particle resulted in the 7 dimensional orbitals. As the periodic table of elements based on the atomic orbitals, the periodic table of elementary particles is based on the combination of the two asymmetrical sets of the 7 dimensional orbitals. One set as the principal dimensional orbitals is mainly for leptons and gauge bosons, and another set as the auxiliary orbitals is mainly for individual quarks. The calculated constituent masses of leptons, quarks, gauge bosons, and the Higgs boson are in good agreement with the observed values. For examples, the calculated mass of top quark is 176.5 GeV in good agreement with the observed 173.34 GeV, and the calculated average mass of the Higgs boson is 128.8 GeV in good agreements with the observed 125 or 126 GeV.
Keywords:The Periodic Table of Elementary Particles, String Theory, Higgs Boson, Lepton, Quark, Gauge Boson

1. Introduction
In conventional string theory with fixed space-time dimension number, the four dimensional space-time results from the compactization of the seven extra space dimensions. There is no experimental proof for compactized extra space dimensions. Another method to account for extra space dimensions is to place the 4D space-time as a subspace of the full dimensional universe as in the Randall-Sundrum model [1] . This paper posits string theory with oscillating space-time dimension number [2] . Dimension number oscillates between 11D and 10D and between 10D and 4D reversibly. There are no extra space dimensions and compactization.
The important phenomena, such as the different masses of elementary particles (leptons, quarks, gauge bosons, and the Higgs boson) cannot be explained clearly by conventional string theory with fixed dimension number, while this paper will show that the masses of elementary particles can be explained and calculated from the periodic table of elementary particles derived directly from string theory with oscillating dimension number. As the periodic table of elements is derived from atomic orbitals, the periodic table of elementary particles is derived from the two asymmetrical sets of seven orbitals where seven comes from the seven extra space dimensions in the eleven-dimensional membrane in string theory with oscillating dimension number. All elementary particles including leptons, quarks, gauge bosons, and the Higgs boson can be placed in the periodic table of elementary particles. The calculated constituent masses are in good agreement with the observed values by using only four known constants: the number of the extra spatial dimensions in the eleven-dimensional membrane, the mass of electron, the mass of Z boson, and the fine structure constant.
In Section 2, string theory with oscillating space-time dimension number is derived from varying speed of light in the framework of special relativity. In Section 3, the digital space structure consists of attachment space (denoted as 1) for rest mass and reversible movement and detachment space (denoted as 0) for irreversible kinetic energy. In Section 4, the proposed cosmology based on string theory and the digital space structure leads to the orbital structure for the periodic table of elementary particles. Section 5 discusses the periodic table of elementary particles.
2. String Theory with Oscillating Dimension Number
In the space-time dimension number oscillation, dimension number oscillates between 11D and 10D and between 10D and 4D for the objects, including 11D membrane (311), 10D string (210), particle (14 to 10), and empty object (04 to 11) [2] . Different universes and different stages of a universe can have different expressions of the object structure. Dimension number varies with varying speed of light and rest mass. Varying speed of light has been proposed to explain the horizon problem of cosmology [3] . J. D. Barrow [4] proposes that the time dependent speed of light varies as some power of the expansion scale factor a in such way that
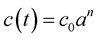 , (1)
, (1)
where 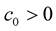 and n are constants. The increase of speed of light is continuous.
and n are constants. The increase of speed of light is continuous.
In this paper, varying dimension number (VDN) relates to quantized varying speed of light (QVSL), where the speed of light is invariant in a constant space-time dimension number, and the speed of light varies with varying space-time dimension number from 4 to 11.
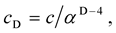 (2)
(2)
where c is the observed speed of light in the 4D space-time, 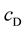 is the quantized varying speed of light in space-time dimension number, D, from 4 to 11, and
is the quantized varying speed of light in space-time dimension number, D, from 4 to 11, and 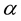 is the fine structure constant for electromagnetism. Each dimensional space-time has a specific speed of light. (Since from the beginning of our observable universe, the space-time dimension has always been four, there is no observable varying speed of light in our observable universe.) The speed of light increases with the increasing space-time dimension number D.
is the fine structure constant for electromagnetism. Each dimensional space-time has a specific speed of light. (Since from the beginning of our observable universe, the space-time dimension has always been four, there is no observable varying speed of light in our observable universe.) The speed of light increases with the increasing space-time dimension number D.
In special relativity,  modified by Equation (2) is expressed as
modified by Equation (2) is expressed as
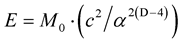 (3a)
(3a)
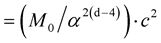 . (3b)
. (3b)
Equation (3a) means that a particle in the D dimensional space-time can have the superluminal speed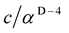 , which is higher than the observed speed of light c, and has the rest mass
, which is higher than the observed speed of light c, and has the rest mass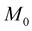 . Equation (3b) means that the same particle in the 4D space-time with the observed speed of light acquires
. Equation (3b) means that the same particle in the 4D space-time with the observed speed of light acquires 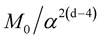 as the rest mass, where d = D. D from 4 to 11 in Equation (3a) is the space-time dimension number defining the varying speed of light. In Equation (3b), d from 4 to 11 is “mass dimension number” defining varying mass. For example, for D = 11, Equation (3a) shows a superluminal particle in eleven-dimensional space-time, while Equation (3b) shows that the speed of light of the same particle is the observed speed of light with the 4D space-time, and the mass dimension is eleven. In other words, with the same total energy, 11D space-time can transform into 4D spacetime with 11d mass dimension. 11D4d in Equation (3a) becomes 4D11d in Equation (3b) through QVSL. QVSL in terms of varying space-time dimension number, D, brings about varying mass in terms of varying mass dimension number, d. Mass dimension is also proposed in the Wesson’s Space-Time-Matter (STM) theory as the matter dimension to account for the extra space dimensions [5] .
as the rest mass, where d = D. D from 4 to 11 in Equation (3a) is the space-time dimension number defining the varying speed of light. In Equation (3b), d from 4 to 11 is “mass dimension number” defining varying mass. For example, for D = 11, Equation (3a) shows a superluminal particle in eleven-dimensional space-time, while Equation (3b) shows that the speed of light of the same particle is the observed speed of light with the 4D space-time, and the mass dimension is eleven. In other words, with the same total energy, 11D space-time can transform into 4D spacetime with 11d mass dimension. 11D4d in Equation (3a) becomes 4D11d in Equation (3b) through QVSL. QVSL in terms of varying space-time dimension number, D, brings about varying mass in terms of varying mass dimension number, d. Mass dimension is also proposed in the Wesson’s Space-Time-Matter (STM) theory as the matter dimension to account for the extra space dimensions [5] .
The QVSL transformation transforms both space-time dimension number and mass dimension number. In the QVSL transformation, the decrease in the speed of light leads to the decrease in space-time dimension number and the increase of mass in terms of increasing mass dimension number from 4 to 11,
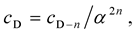 (4a)
(4a)
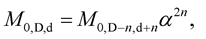 (4b)
(4b)
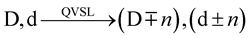 (4c)
(4c)
where D is the space-time dimension number from 4 to 11 and d is the mass dimension number from 4 to 11. For example, in the QVSL transformation, a particle with 11D4d is transformed to a particle with 4D11d. In terms of rest mass, 11D space-time has 4d with the lowest rest mass, and 4D space-time has 11d with the highest rest mass.
The fine structure constant, 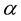 , is also used for the calculation of the masses of elementary particle by A. O.
, is also used for the calculation of the masses of elementary particle by A. O.
Barut [6] in the lepton mass formula  where mN is the masses of leptons, me is the mass of electron, and N is an integer variable and by Karl Otto Greulich [7] [8] in the similar elementary particle mass equation:
where mN is the masses of leptons, me is the mass of electron, and N is an integer variable and by Karl Otto Greulich [7] [8] in the similar elementary particle mass equation: 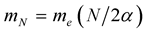 where mN is the masses of elementary particles. The calculated masses [6] [7] are in good agreement with the observed values. In this paper,
where mN is the masses of elementary particles. The calculated masses [6] [7] are in good agreement with the observed values. In this paper, 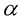 is used to calculate the masses of leptons, quarks, gauge bosons, and the Higgs boson.
is used to calculate the masses of leptons, quarks, gauge bosons, and the Higgs boson.
3. The Space Structure
The dimension number oscillation is reversible, so it occurs only in the space without irreversible kinetic energy. Such space is attachment space in the digital space structure. The digital space structure [9] consists of attachment space (denoted as 1) and detachment space (denoted as 0). Attachment space attaches to object permanently with zero speed. Detachment space detaches from the object at the speed of light. Attachment space relates to rest mass, while detachment space relates to irreversible kinetic energy. Different stages of our universe have different space structures.
The transformation between mass (massive particle) in attachment space and kinetic energy (massless particle) in detachment space is through the scalar Goldstone boson. The Goldstone boson in the Standard Model for electroweak interaction is the Higgs boson [10] .
4. Cosmology
A simplified version of cosmology from the Reference [2] for the periodic table of elementary particles can be described by space-time dimension number (D) and mass dimension (d) without many other details. Our universe started from 11D4d membranes. With the emergence of empty object, 11D4d membranes transformed into non-gravitational 10D4d strings warped with gravitational 10D4d particles.
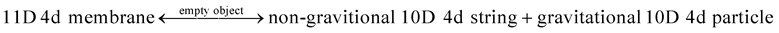 (5)
(5)
Empty object corresponds to the anti-De Sitter bulk space in the Randall-Sundrum model [1] for gravity. Gravity is in the bulk space, which is the warped space (transverse radial space) around the 10D4d strings. As in the AdS/CFT duality [11] for gravity, the non-gravitational force has 10D dimension, one dimension lower than the 11D membrane, and is the conformal force defined on the conformal boundary of the bulk space.
As described in Reference [2] , with electromagnetic charge, the non-gravitational 10D4d strings transformed into the non-gravitational 10D4d particles.
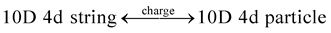 (6)
(6)
The non-gravitational 10D4d particles transformed into the 4D10d particle for the inflation before the Big Bang.
 (7)
(7)
By detachment space (denoted as 0), the 4D10d particles (denoted as 1) were sliced into 4D4d core particles surrounded by 6 mass dimensions as the dimensional orbitals as follows.
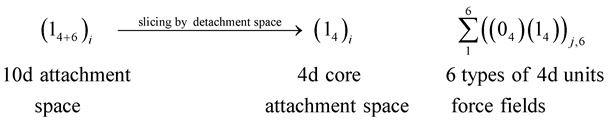 (8)
(8)
where i is for the number of units of core particles and j is for the number of units of 4D4d quantized units of force fields. The two products of the slicing are the 4d-core attachment space and 6 types of 4d quantized units. The 4d core attachment space surrounded by 6 types of many (j) 4D4d quantized units corresponds to the core particle surrounded by 6 types of many small 4d particles, which constitute gauge force fields in “dimensional orbitals”.
Some of the gravitational 10D4d particles also transformed into 4D10d particles to join the 6 non-gravitational dimensional orbitals, resulting in the7 dimensional orbitals as in Figure 1.
The seven dimensional orbitals are arranged in the order of mass dimension numbers from 5d (the lowest mass) to 11d (the highest mass as the Planck mass). The precise relation between adjacent orbitals is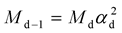 . From the mass of electron at d = 5, the calculated Planck mass at d = 11 is 1.1 ´ 1019 GeV in good agreement with the Planck mass, 1.2 ´ 1019 GeV as shown in Table3
. From the mass of electron at d = 5, the calculated Planck mass at d = 11 is 1.1 ´ 1019 GeV in good agreement with the Planck mass, 1.2 ´ 1019 GeV as shown in Table3
5. The Periodic Table of Elementary Particles
Some particles-antiparticles at the beginning of the Big Bang are not symmetrical, instead of radiation resulted from the symmetrical particles-antiparticles. It consists of two four dimensional particles each with its own set of seven “dimensional orbitals”. The seven dimensional orbitals represent originally the seven extra spatial dimensions in the eleven dimensional membrane of string theory.
One four dimensional particle has the seven “principal dimensional orbitals”, while the other four dimensional particle has the seven “auxiliary dimensional orbitals” that are superimposed on the seven principal dimensional orbitals. (In nature, the elementary fermions are distinctively divided into leptons and quarks, so there are two distinctively different dimensional orbitals consisting of principal dimensional orbitals mainly for leptons and auxiliary dimensional orbitals mainly for quarks.). The auxiliary orbitals are dependent on the principal orbitals, so only one set of dimensional orbitals appears. The principal dimensional orbitals are mainly for leptons and gauge bosons, and the auxiliary dimensional orbitals are mainly for individual quarks. Because of the dependence of the auxiliary dimensional orbitals, individual quarks are hidden. The configuration of dimensional orbitals and the periodic table of elementary particles are shown in Figure 2 and Tables 1-3.

Figure 1. The seven mass dimensions as dimensional orbitals.
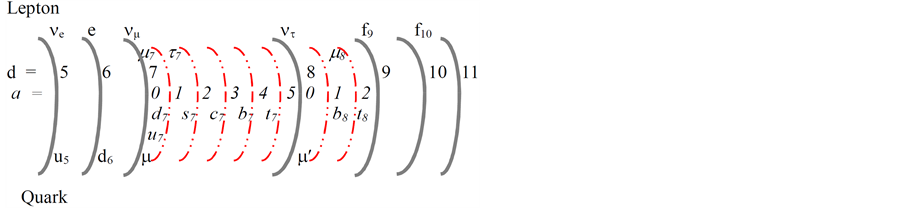
Figure 2. Leptons and quarks in the seven principal dimensional orbitals (solid lines) denoted by the principal dimensional orbital number d and the seven auxiliary dimensional orbitals (dashdotted lines) denoted by the auxiliary dimensional number a.
Table 1. The periodic table of elementary particles. d = principal dimensional orbital number, a = auxiliary dimensional orbital number.
Table 2. The compositions and the constituent masses of leptons and quarks. d = principal dimensional orbital number and a = auxiliary dimensional orbital number.
Table 3. The Masses of the dimensional orbital gauge bosons: a = ae, d = dimensional orbital number.
Figure 2 shows leptons and quarks. The symbols of the top row represent leptons and their components. ne, e, nμ, and nt are on the principal dimensional orbitals, 5, 6, 7, and 8, respectively. Other leptons (m, τ, and m’) are the composites of both the principal components (e and n) and auxiliary components (m7, t7 and m8) as shown in Table2 The subscript numbers of leptons and quarks denote the principal orbital numbers. All quarks are the composites of both principal components (u5, d6, m, and m’) and auxiliary components (u7, d7, s7, c7, b7, t7, b8, and t8) as shown in Table2 In the second column of Table 2, the main number denotes the principal orbital number, and the subscript number denotes the auxiliary orbital number.
The first auxiliary orbital starts from the principal orbital d = 7, because the first possible lepton m involved in the auxiliary orbital starts from d = 7. There are only five auxiliary dimensional orbitals between the principal dimensional orbitals d = 7 and d = 8, because the energy level of the sixth auxiliary dimensional orbital a = 6 is higher than the energy level of the principal dimensional orbital d = 8. The seven auxiliary dimensional orbitals can accommodate only three families of lepton-quark as in the Standard Model. No leptons and quarks appear on and higher than d = 9, which is outside of the Standard Model and the seven auxiliary dimensional orbitals. f9 and f10 are the principal fermions on d = 9 and 10, respectively. The gauge bosons are not shown, and can be located on the top row at principal dimensional orbitals as shown in Table1
Table 1 shows leptons, quarks, and gauge bosons. For leptons, the leptons at a = 0 are the principal leptons (ne, e, nμ, and nt). Other leptons (m, τ, and m’) are the composites of both the principal components (e and n at a = 0) and auxiliary components (m7, t7 and m8 at a > 0) as shown in Table2 All quarks are the composites of both principal components (u5, d6, m, and m’ at a = 0) and auxiliary components (u7, d7, s7, c7, b7, t7, b8, and t8 at a > 0) as shown in Table2 Outside of the Standard Model, m’ is hidden, and is balanced by the hidden b8. No leptons and quarks appear on and higher than d = 9, which is outside of the Standard Model and the seven auxiliary dimensional orbitals. The bosons, B5, B6, B7, B8, B9, B10, and B11 are shown in Table3
The principal dimensional orbitals are for gauge bosons of the force fields, as shown in Table1 It will be shown shortly that Fd has lower energy than Bd, and similarly the seven principal dimensional orbitals are arranged as F5 B5 F6 B6 F7 B7 F8 B8 F9 B9 F10 B10 F11 B11, where B and F are the boson and fermion in each orbital. The previous communications [12] shows that the masses of fundamental particles are related to each other with three simple formulae, and that the use of accepted mass data allows calculation of masses of many other particles. The formulae are
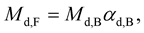 (9a)
(9a)
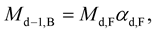 (9b)
(9b)
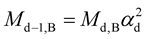 , (9c)
, (9c)
where d is the dimensional orbital number from 6 to 11. Each dimension has its own ad, and all ad’s except a7 (aw) of the seventh dimension (weak interaction) are equal to a, the fine structure constant of electromagnetism. In Equation (9), different fermions and bosons with different d’s have different starting masses and coupling constants based on the non-perturbative calculation for the starting masses and coupling constants from Equation (9). Each starting mass or coupling constant then has its own running mass or coupling constant based on the perturbative beta function where running coupling constant changes logarithmically with energies.
The bosons generated in this manner are the dimensional orbital bosons or BD as shown in Table3
In Table 3, a = ae (the fine structure constant for electromagnetic field), MZ = Mw/cosqw, and aw = a/sin2qw [13] . aw is not same as ae because there is a mixing between B5 and B7 as the symmetry mixing between U(1) and SU(2) in the standard theory of the electroweak interaction, and sinqw is not equal to 1. The calculated value for aw is 0.02973, and sin2qw is 0.2454 in good agreement with 0.2312 for the observed value of sin2qw [14] .
The lowest energy boson (B5) at d = 5 is the Coulomb field for electromagnetism. The second lowest boson (B6) at d = 6 is p1/2 (a spin 1 boson as a half of the spin 0 pion) for the strong interaction. The pion theory [15] where pions mediate the strong interaction works well at long enough distances (longer than the nucleon radius) or low enough energies. At short enough distances (shorter than the nucleon radius) or high enough energies, gluons emerge. In this paper, gluons are derived from the need to hide the auxiliary dimensional orbitals. As mentioned previously, leptons are derived mostly from the seven principal dimensional orbitals, while quarks are derived mostly from the seven auxiliary dimensional orbitals. Only the seven principal dimensional orbitals for leptons are revealed, while the seven auxiliary dimensional orbitals for quarks are hidden to preserve the seven apparent total dimensional orbitals instead of the fourteen apparent total dimensional orbitals. As a result, gluons emerge at the short distances to mediate the strong interaction among quarks in order to confine or hide isolated quarks (the auxiliary dimensional orbitals) within nucleons, while at the long distances without isolated quarks outside of nucleon at low energies, pions emerge to mediate the residual strong interaction for the nucleon-nucleon interaction or the nuclear force (At low energies or long distances, gluons based on the negative perturbative beta function in QCD do not work due to the infrared divergence [16] ). Although all of the gauge bosons in the Standard Model are originated from the local gauge symmetry, only gluon results in the confinement, while all other gauge bosons do not result in any kind of confinement.
The third lowest boson (B7) at d = 7 is Z0 for the weak interaction. In the Standard Model, W± bosons and Z boson are related. The mass of W bosons is equal to the mass of Z boson times cosqw. Like photon at d = 5, Z is neutral, so Z instead of W± is the dimensional boson at d = 7. The highest energy boson (B11) is has the mass of the Planck mass for gravity. The calculated energy for B11 is 1.1 × 1028 eV in good agreement with the Planck mass, 1.2 × 1028 eV.
Auxiliary dimensional orbital is derived from principal dimensional orbital. It is for high-mass leptons and individual quarks. The combination of dimensional auxiliary dimensional orbitals constitutes the periodic system for elementary particles as shown in Figure 1 and Table1 There are two types of fermions in the periodic table of elementary particles: low-mass leptons and high-mass leptons and quarks. Low-mass leptons include ne, e, nm, and nt, which are in principal dimensional orbital, not in auxiliary dimensional orbital. ld is denoted as lepton with principal dimension number, d, l5, l6, l7, and l8 are ne, e, nm, and nt, respectively. All neutrinos have zero mass because of chiral symmetry (permanent chiral symmetry).
High-mass leptons and quarks include m, t, u, d, s, c, b, and t, which are the combinations of both principal dimensional fermions and auxiliary dimensional fermions. Each fermion can be defined by principal dimensional orbital numbers (d’s) and auxiliary dimensional orbital numbers (a’s) as da in Table2 For examples, e is 60 that means it has d (principal dimensional orbital number) = 6 and a (auxiliary dimensional orbital number) = 0, so e is a principal dimensional fermion. High-mass leptons, m and t, are the combinations of principal dimensional fermions, e and nm, and auxiliary dimensional fermions. For example, m is the combination of e, nm, and m7, which is 71 that has d = 7 and a = 1.
Quarks are the combination of principal dimensional quarks (qd) and auxiliary dimensional quarks. The principal dimensional fermion for quark is derived from principal dimensional lepton. To generate a principal dimensional quark in principal dimensional orbital from a lepton in the same principal dimensional orbital is to add the lepton to the boson from the combined lepton-antilepton. Thus, the mass of the quark is three times of the mass of the corresponding lepton in the same dimension. The equation for the mass of principal dimensional fermion for quark is
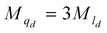 (10)
(10)
For principal dimensional quarks, q5 (50) and q6 (60) are 3ne and 3e, respectively. Since l7 is massless nm, nm is replaced by m, and q7 is 3m. Quarks are the combinations of principal dimensional quarks, qd, and auxiliary dimensional quarks. For example, s quark is the combination of q6 (3e), q7 (3m) and s7 (auxiliary dimensional quark = 72).
The principal dimensional fermion for heavy leptons (m and t) is e and ne. Auxiliary dimensional fermion is derived from principal dimensional boson in the same way as Equation (1) to relate the energies for fermion and boson. For the mass of auxiliary dimensional fermion (AF) from principal dimensional boson (B), the equation is Equation (11).
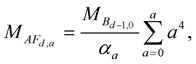 (11)
(11)
where aa = auxiliary dimensional fine structure constant, and a = auxiliary dimension number = 0 or integer.
The first term, 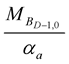 , of the mass formula (Equation (11)) for the auxiliary dimensional fermions is derived from the mass equation, Equation (1), for the principal dimensional fermions and bosons. The second term,
, of the mass formula (Equation (11)) for the auxiliary dimensional fermions is derived from the mass equation, Equation (1), for the principal dimensional fermions and bosons. The second term,
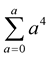 , of the mass formula is for Bohr-Sommerfeld quantization for a charge-dipole interaction in a circular orbit as described by A. Barut [6] . As in Barut lepton mass formula, 1/aa is 3/2. The coefficient, 3/2, is to convert the principal dimensional boson mass to the mass of the auxiliary dimensional fermion in the higher dimension by adding the boson mass to its fermion mass which is one-half of the boson mass. Using Equation (9), Equation (11) becomes the formula for the mass of auxiliary dimensional fermions (AF).
, of the mass formula is for Bohr-Sommerfeld quantization for a charge-dipole interaction in a circular orbit as described by A. Barut [6] . As in Barut lepton mass formula, 1/aa is 3/2. The coefficient, 3/2, is to convert the principal dimensional boson mass to the mass of the auxiliary dimensional fermion in the higher dimension by adding the boson mass to its fermion mass which is one-half of the boson mass. Using Equation (9), Equation (11) becomes the formula for the mass of auxiliary dimensional fermions (AF).
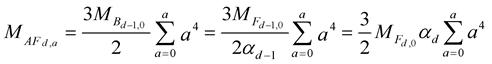 (12)
(12)
The mass of this auxiliary dimensional fermion is added to the sum of masses from the corresponding principal dimensional fermions (F’s) with the same electric charge or the same dimension. The corresponding principal dimensional leptons for u (2/3 charge) and d (−1/3 charge) are ne (0 charge) and e (−1 charge), respectively, by adding −2/3 charge to the charges of u and d [17] . The fermion mass formula for heavy leptons is derived as follows.
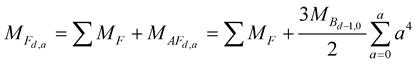 (13a)
(13a)
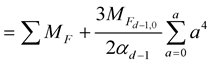 (13b)
(13b)
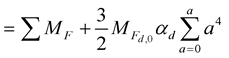 (13c)
(13c)
Equation (13b) is for the calculations of the masses of leptons. The principal dimensional fermion in the first term is e. Equation (13b) can be rewritten as Equation (14).
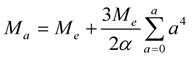 , (14)
, (14)
a = 0, 1, and 2 are for e, m, and t, respectively. It is identical to the Barut lepton mass formula.
The auxiliary dimensional quarks except a part of t quark are q7’s. Equation (13c) is used to calculate the masses of quarks. The principal dimensional quarks include 3nm, 3e, and 3m., a7 = aw, and q7 = 3m. Equation (13c) can be rewritten as the quark mass formula.
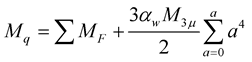 , (15)
, (15)
where a = 1, 2, 3, 4, and 5 for u/d, s, c, b, and a part of t, respectively.
To match l8 (nt), quarks include q8 as a part of t quark. In the same way that q7 = 3m, q8 involves m’. m’ is the sum of e, m, and m8 (auxiliary dimensional lepton). Using Equation (11), the mass of m8 is equal to 3/2 of the mass of B7, which is Z0. Because there are only three families for leptons, m’ outside of standard three families is the extra lepton, which is “hidden”. The principal dimensional quark q8 = m’ instead of 3m’, because m’ is hidden, and q8 does not need to be 3m’ to be different. Using the equation similar to Equation (15), the calculation for t quark involves a8 = a, m’ instead of 3m for principal fermion, and a = 1 and 2 for b8 and t8, respectively. The hiding of m’ for leptons is balanced by the hiding (zero value) of b8 for quarks.
All leptons and quarks with d’s, a’s and the calculated masses are listed in Table2 Table 2 shows the compositions of leptons and quarks. Each fermion can be defined by principal dimensional orbital numbers (d’s) and auxiliary dimensional orbital numbers (a’s). For examples, e is 60 that means it has d (principal dimensional orbital number) = 6 and a (auxiliary dimensional orbital number) = 0, so e is a principal dimensional fermion. All neutrinos are nearly massless because of chiral symmetry (permanent chiral symmetry). As shown in Table 2, m’ and m’± are the hidden (forbidden) leptons outside of the three lepton families in the Standard Model. All elementary particles (gauge bosons, leptons, and quarks) are in the periodic table of elementary particles with the calculated constituent masses in good agreement with the observed values [18] [19] by using only four known constants: the number of the extra spatial dimensions in the eleven-dimensional membrane, the mass of electron, the mass of Z boson, and the fine structure constant. For an example, the calculated mass of top quark is 176.5 GeV in good agreement with the observed 173.34 GeV [20] . At the high energy of top quark, there is very little binding energy. Without the complication of binding energies as in low energy quarks, the observed mass of top quark is in good agreement with the calculated mass without binding energy.
In Reference [10] , it is proposed that the observed Higgs Boson at the LHC [21] [22] is the Standard Model Higgs boson that adopts the existence of the hidden lepton condensate. The hidden lepton is in the forbidden lepton family, outside of the three lepton families of the Standard Model. Being forbidden, a single hidden lepton cannot exist alone; so it must exist in the lepton condensate as a composite of m’ and m’± hidden leptons and their corresponding anti leptons. The calculated average mass of the Higgs boson is 128.8 GeV in good agreements with the observed 125 or 126 GeV.
6. Summary
In this paper, all elementary particles (leptons, quarks, gauge bosons, and the Higgs boson) can be placed in the periodic table of elementary particles based on string theory with oscillating space-time dimension number, instead of conventional string theory with fixed space-time dimension number. Dimension number oscillates between 11D and 10D and between 10D and 4D reversibly. The oscillation of space-time dimension number (D) is accompanied by mass dimension number (d) to represent mass. Space-time dimension number decreases with increasing mass dimension number, decreasing speed of light and increasing rest mass. 4D particle originally is 4D10d particle, and has the lowest speed of light and the highest rest mass. With the same energy, the relation between adjacent mass dimensions is 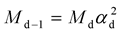 where M is rest mass, d is mass dimension number, and α is the fine structure constant. According to the proposed cosmology, the non-gravitational 4D10d particles were sliced into 4D4d core particles surrounded by 6 separated mass dimensions as the 6 dimensional orbitals constituting the non-gravitational forces (electromagnetism, strong, and weak). The combination of the 6 dimensional orbitals and the gravitational 4D10d particle resulted in the 7 dimensional orbitals. As the periodic table of elements based on the atomic orbitals, the periodic table of elementary particles is based on the combination of the two asymmetrical sets of the 7 dimensional orbitals. One set as the principal dimensional orbitals is mainly for leptons and gauge bosons, and another set as the auxiliary orbitals is mainly for individual quarks. The calculated constituent masses of leptons, quarks, gauge bosons, and the Higgs boson are in good agreement with the observed values. For examples, the calculated mass of top quark is 176.5 GeV in good agreement with the observed 173.34 GeV, and the calculated average mass of the Higgs boson is 128.8 GeV in good agreements with the observed 125 or 126 GeV.
where M is rest mass, d is mass dimension number, and α is the fine structure constant. According to the proposed cosmology, the non-gravitational 4D10d particles were sliced into 4D4d core particles surrounded by 6 separated mass dimensions as the 6 dimensional orbitals constituting the non-gravitational forces (electromagnetism, strong, and weak). The combination of the 6 dimensional orbitals and the gravitational 4D10d particle resulted in the 7 dimensional orbitals. As the periodic table of elements based on the atomic orbitals, the periodic table of elementary particles is based on the combination of the two asymmetrical sets of the 7 dimensional orbitals. One set as the principal dimensional orbitals is mainly for leptons and gauge bosons, and another set as the auxiliary orbitals is mainly for individual quarks. The calculated constituent masses of leptons, quarks, gauge bosons, and the Higgs boson are in good agreement with the observed values. For examples, the calculated mass of top quark is 176.5 GeV in good agreement with the observed 173.34 GeV, and the calculated average mass of the Higgs boson is 128.8 GeV in good agreements with the observed 125 or 126 GeV.
References
- Randall, L. and Sundrum, R. (1999) Physical Review Letters, 83, 4690-4693. http://dx.doi.org/10.1103/PhysRevLett.83.4690
- Chung, D.-Y. (2014) Journal of Modern Physics, 5, 464-472. http://dx.doi.org/10.4236/jmp.2014.56056
- Albrecht, A. and Magueijo, J. (1999) Physics Review, D59, Article ID: 043516. http://dx.doi.org/10.1103/PhysRevD.59.043516
- Barrow, J.D. (2003) Physics Letter B, 564, 1-7. http://dx.doi.org/10.1016/S0370-2693(03)00573-2
- Wesson, P.S. (1999) Space-Time-Matter: Modern Kaluza-Klein Theory. World Scientific Publishing Company, Singapore. http://dx.doi.org/10.1142/9789812385475
- Barut, A.O. (1979) Physical Review Letter, 42, 1251. http://dx.doi.org/10.1103/PhysRevLett.42.1251
- Greulich, K.O. (2010) Journal of Modern Physics, 1, 300-302. http://dx.doi.org/10.4236/jmp.2010.15042
- Greulich, K.O. (2013) Proceedings of SPIE, 8832, Article ID: 883218. http://dx.doi.org/10.1117/12.2023044
- Chung, D.-Y. and Krasnoholovets, V. (2013) Journal of Modern Physics, 4, 27-31. http://dx.doi.org/10.4236/jmp.2013.44A005
- Chung, D.-Y. and Hefferlin, R. (2013) Journal of Modern Physics, 4, 21-26. http://dx.doi.org/10.4236/jmp.2013.44A004
- Maldacena, J. (1998) Advances in Theoretical and Mathematical Physics, 2, 231-252.
- Chung, D. (1997) Speculations in Science and Technology, 20, 259-268. http://dx.doi.org/10.1023/A:1026433207862
- Salam, A. (1968) Svartholm, W., Ed., Elementary Particle Theory, Almquist and Wiksell, Stockholm, 367-387.
- Beringer, J., et al. (2012) Physical Review, D86, Article ID: 0100018 http://pdg.lbl.gov/2012/reviews/rpp2012-rev-standard-model.pdf
- Fujita, J. and Miyazawa, H. (1957) Progress of Theoretical Physics, 17, 360. http://dx.doi.org/10.1143/PTP.17.360
- Aguilar, A., Binosi, D. and Papavassiliou, J. (2008) Physical Review, D 78, Article ID: 025010. http://dx.doi.org/10.1103/PhysRevD.78.025010
- Langacher, P., Luo, M. and Mann, A. (1992) Reviews of Modern Physics, 64, 87-192. http://dx.doi.org/10.1103/RevModPhys.64.87
- Griffiths, D. (2008) Introduction to Elementary Particles. WILEY-VCH, 135.
- MacGregor, M.H. (2005) International Journal of Modern Physics A, 20, 719-798. http://dx.doi.org/10.1142/S0217751X05021117
- The ATLAS, CDF, CMS, D0 Collaborations (2014) First Combination of Tevatron and LHC Measurements of the Top-Quark Mass. arXiv:1403.4427 [hep-ex]
- The ATLAS Collaboration (2012) Physical Letters B, 716, 1-29. http://dx.doi.org/10.1016/j.physletb.2012.08.020
- The CMS Collaboration (2012) Physical Letters B, 716, 30-61. http://dx.doi.org/10.1016/j.physletb.2012.08.021


