Journal of Modern Physics
Vol.5 No.5(2014), Article ID:44083,6 pages DOI:10.4236/jmp.2014.55027
On the Heisenberg and Schrödinger Pictures
Shigeji Fujita1, James MacNabb III1, Akira Suzuki2
1Department of Physics, University at Buffalo, State University of New York, Buffalo, USA
2Department of Physics, Faculty of Science, Tokyo University of Science, Tokyo, Japan
Email: asuzuki@rs.kagu.tus.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 December 2013; revised 8 January 2014; accepted 3 February 2014
ABSTRACT
A quantum theory for a one-electron system can be developed in either Heisenberg picture or Schrödinger picture. For a many-electron system, a theory must be developed in the Heisenberg picture, and the indistinguishability and Pauli’s exclusion principle must be incorporated. The hydrogen atom energy levels are obtained by solving the Schrödinger energy eigenvalue equation, which is the most significant result obtained in the Schrödinger picture. Both boson and fermion field equations are nonlinear in the presence of a pair interaction.
Keywords:Heisenberg and Schrödingier Pictures; Many-Particle Systems; Indistinguishability; Second Quantization; Pauli’s Exclusion Principle

1. Introduction
Both Heisenberg (HP) and Schrödinger pictures (SP) are used in quantum theory. Schrödinger solved Schrö- dinger eigenvalue equation for a hydrogen atom, and obtained the atomic energy levels. Heisenberg discussed the uncertainty principle based on the fundamental commutation relations. Both pictures are equivalent in dealing with a one-electron system. In dealing with many electrons or many photons a theory must be developed in the HP, incorporating the indistinguishability and Pauli’s exclusion principle. A quantum theory must give a classical result in some limit. We will see that this limit is represented by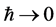 . The HP, and not the SP, give the correct results for a many-particle system. The quantum field equation is nonlinear if a pair interaction exists.
. The HP, and not the SP, give the correct results for a many-particle system. The quantum field equation is nonlinear if a pair interaction exists.
2. One Electron Systems
We consider an electron in a potential energy field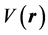 , where
, where 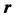 is a position vector. In the Cartesian representation
is a position vector. In the Cartesian representation
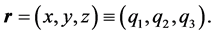 (1)
(1)
The canonical momentum 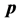 is
is
![]() (2)
(2)
The Hamiltonian 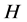 of the system is
of the system is
![]() (3)
(3)
In the HP the coordinates and momenta 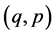 are regarded as Hermitean operators satisfying the fundamental commutation relations (quantum conditions):
are regarded as Hermitean operators satisfying the fundamental commutation relations (quantum conditions):
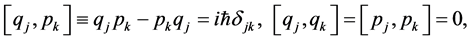 (4)
(4)
where  is Kronecker’s delta
is Kronecker’s delta
 (5)
(5)
and ,
, 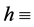 Planck constant.
Planck constant.
The equations of motion for 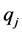 and
and 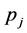 are
are
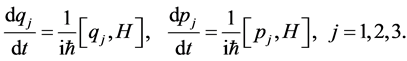 (6)
(6)
The two equations can be included in a single equation:
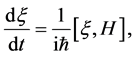 (7)
(7)
where 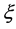 represent any physical observable made out of the components of the position
represent any physical observable made out of the components of the position 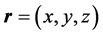 and momentum
and momentum![]() . The angular momentum
. The angular momentum ![]() can be included also. Dirac has shown that in the small
can be included also. Dirac has shown that in the small 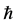 limit:
limit:
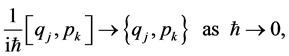 (8)
(8)
where
 (9)
(9)
is the classical Poisson brackets.
In the SP we use the equivalence relations:
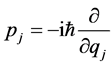 (10)
(10)
and write down the Schrödinger wave equation as
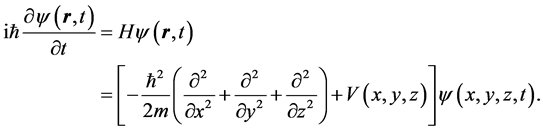 (11)
(11)
The function 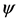 is called the wave function. Normally, it is normalized such that
is called the wave function. Normally, it is normalized such that
![]() (12)
(12)
where 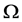 is a normalization volume. The quantum average of an observable
is a normalization volume. The quantum average of an observable 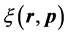 is defined by
is defined by
![]() (13)
(13)
If we use Dirac’s ket and bra notations, then we can see the theoretical structures more compactly [1] . The quantum state 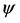 is represented by the ket vector
is represented by the ket vector 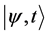 or the bra vector
or the bra vector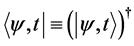 . The Schrödinger equation of motion is
. The Schrödinger equation of motion is
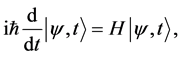 (14)
(14)
whose Hermitean conjugate is
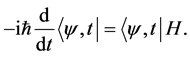 (15)
(15)
If we use the position representation and write
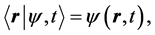 (16)
(16)
then we obtain Equation (11) from Equation (14).
We introduce the density operator 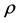 defined by
defined by
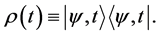 (17)
(17)
Using Equations (14) and (15), we obtain
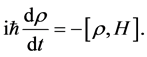 (18)
(18)
This equation, called the quantum Liouville equation, has a reversed sign compared with the equation of motion for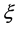 , see Equation (7).
, see Equation (7).
We can express the quantum average 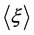 of an observable
of an observable 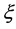 as
as
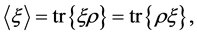 (19)
(19)
where 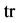 denotes a one-particle trace. Operators under a trace commute.
denotes a one-particle trace. Operators under a trace commute.
We assume that the Hamiltonian 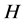 in Equation (11) is a constant of motion. Then, Equation (14) can be reduced to the energy
in Equation (11) is a constant of motion. Then, Equation (14) can be reduced to the energy ![]() eigenvalue equation:
eigenvalue equation:
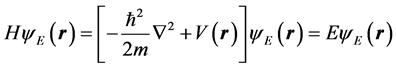 (20)
(20)
after using a separation of variable method for solving Equation (11). Equation (20) is known as the Schrödinger energy-eigenvalue equation. The hydrogen atom energy-levels can be obtained from Equation (20) with![]() ,
, 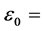 permittivity.
permittivity.
Except for simple systems such as free electrons and simple harmonic oscillators, the Heisenberg equation of motion (7) [or the quantum Liouville Equation (18)] are harder to solve. This is so because the numbers of unknowns in the 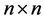 matrix are more numerous than in the
matrix are more numerous than in the 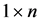 vector.
vector.
3. Difficulties with the SP
The following items have difficulties in the SP. They cannot be addressed properly.
(a) The Classical Mechanical Limit 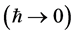
Dirac showed that the fundamental commutation relations (8) can also be applied to a many particle system only if the Cartesian coordinates and momenta are used. The equation of motion (7) in the HP can be reduced to the classical equation of motion:
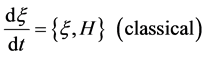 (21)
(21)
in the classical limit
 (22)
(22)
The Schrödinger equation of motion (11) does not have such a simple limit.
(b) Indistinguishability All electrons are identical (indistinguishable) to each other. This is known as the indistinguishability. This property can be stated as follows:
Consider a system of 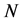 electrons interacting with each other characterized by the Hamiltonian:
electrons interacting with each other characterized by the Hamiltonian:
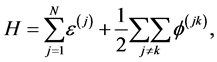 (23)
(23)
where ![]() is the kinetic energy and
is the kinetic energy and 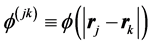 is the pair interaction energy. Here the upper indices
is the pair interaction energy. Here the upper indices  and
and 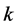 denote the electrons. The indistinguishability requires that
denote the electrons. The indistinguishability requires that
 (24)
(24)
where 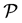 are the permutation operators. For a three-particle system the permutation operators are
are the permutation operators. For a three-particle system the permutation operators are
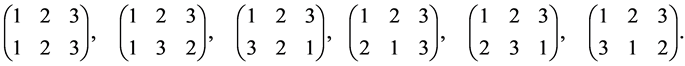 (25)
(25)
The order of the permutation group for an  -particle system is
-particle system is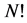 . The total momentum, the total angular momentum, and the total mass satisfy the same Equation (24). We may express this by
. The total momentum, the total angular momentum, and the total mass satisfy the same Equation (24). We may express this by
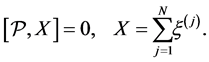 (26)
(26)
(c) Boson Creation and Annihilation Photons are bosons with full spin. They can be created and annihilated spontaneously. These processes can only be described by using creation and annihilation operators ![]() both of which move, following the Heisenberg equations of motion. One can no more limit the number of bosons in the system.
both of which move, following the Heisenberg equations of motion. One can no more limit the number of bosons in the system.
(d) The Second Quantization for Bosons Bosons can be treated using second-quantized operators ![]() satisfying the Bose commutation rules:
satisfying the Bose commutation rules:
 (27)
(27)
where  indicates particle states. Both operators
indicates particle states. Both operators 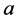 and
and  move, following the Heisenberg equations of motion, e.g.
move, following the Heisenberg equations of motion, e.g.
 (28)
(28)
where 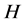 is a many-boson Hamiltonian. The Hamiltonian for free photons is given by
is a many-boson Hamiltonian. The Hamiltonian for free photons is given by
 (29)
(29)
where 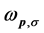 is angular frequency and
is angular frequency and 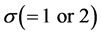 denotes the polarization indices.
denotes the polarization indices.
(e) The Second Quantization for Fermions Many fermions can be treated by using the complex dynamical operators ![]() satisfying the Fermi anticommutation rules:
satisfying the Fermi anticommutation rules:
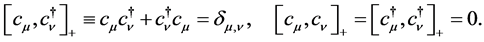 (30)
(30)
Both operators 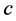 and
and 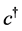 move, following the Heisenberg equations of motion.
move, following the Heisenberg equations of motion.
If the system contains many electrons, then we must consider Pauli’s exclusion principle that no more than one fermion can occupy the same particle state. This is a restriction which cannot be described without considering permutation symmetry.
(f) Holes Dirac showed [1] that there is symmetry between the occupied and unoccupied states for fermions, based on second quantization calculations. Holes are as much physical particles as electrons, and are fermions.
All six properties (a) - (f) can be discussed in the HP, but not in the SP. The last five (b) - (f) concern many-particle systems.
4. Discussion
We first discuss two relevant topics.
(a) Wave packets Dirac assumed [1] that an experimentally observed particle correspond to a wave packet composed of the quantum waves, and showed that any wave packet moves obeying the classical mechanical laws of motion.
(b) The classical statistical limit Free fermions (bosons) in equilibrium obey the Fermi (Bose) distribution law:
 (31)
(31)
where 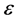 is the kinetic energy,
is the kinetic energy, 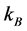 the Boltzmann constant,
the Boltzmann constant,  the absolute temperature and
the absolute temperature and 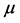 the chemical potential; the upper (lower) signes correspond to the Fermi (Bose) distribution functions. In the classical statistical limit, which is realized in either low density
the chemical potential; the upper (lower) signes correspond to the Fermi (Bose) distribution functions. In the classical statistical limit, which is realized in either low density 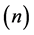 limit or high temperature
limit or high temperature ![]() limit, both distribution functions
limit, both distribution functions  approach the classical Boltzmann distribution function:
approach the classical Boltzmann distribution function:
![]() (32)
(32)
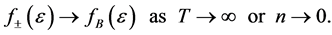 (33)
(33)
For illustration we consider a free electron model for a metallic body-centred cubic (bcc) crystal such as sodium. Electrons subject to the exclusion principle are fermions which obey the Fermi distribution law. The heat capacity 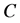 at the low temperatures
at the low temperatures 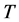 shows a
shows a  -linear behavior. Phonons which are quanta of the lattice vibrations are bosons and they obey the Planck distribution law:
-linear behavior. Phonons which are quanta of the lattice vibrations are bosons and they obey the Planck distribution law:
 (34)
(34)
since the chemical potential 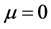 for phonons. The heat capacity arising from the phonons at low temperatures shows Debye
for phonons. The heat capacity arising from the phonons at low temperatures shows Debye 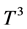 -law [2] . The electron wave packets have a linear size of the order of the lattice constant of the bcc crystal. The average phonon size is much greater, and is distributed with the Planck’s law.
-law [2] . The electron wave packets have a linear size of the order of the lattice constant of the bcc crystal. The average phonon size is much greater, and is distributed with the Planck’s law.
The effects of quantum statistics which involve 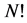 permutations, see Equation (24), are much stronger than the effects of quantum entangling that grows linearly with
permutations, see Equation (24), are much stronger than the effects of quantum entangling that grows linearly with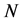 .
.
Let us introduce boson field operators 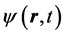 and
and ![]() which satisfy the Bose commutation rules:
which satisfy the Bose commutation rules:
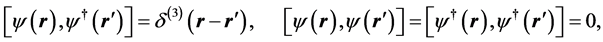 (35)
(35)

where
![]() (36)
(36)
and 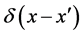 is Dirac’s delta-function.
is Dirac’s delta-function.
A quantum many-boson Hamiltonian 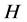 corresponding to the Hamiltonian in Equation (23) is
corresponding to the Hamiltonian in Equation (23) is
![]()
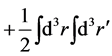
![]()
 (37)
(37)
where ![]() are the field operators satisfying the equal-time commutation rules (35). The field equation is obtained from the Heisenberg Equation (28) as follows:
are the field operators satisfying the equal-time commutation rules (35). The field equation is obtained from the Heisenberg Equation (28) as follows:
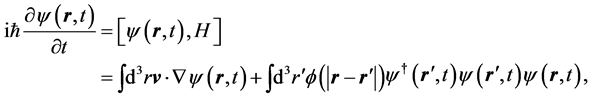 (38)
(38)
where 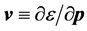 is the velocity vector. We note that the field equation is nonlinear in the presence of a pair potential. This equation can be used to derive, and obtain the time dependent version of the Ginzburg-Landau (GL) equation [3] . This topic will be treated separately.
is the velocity vector. We note that the field equation is nonlinear in the presence of a pair potential. This equation can be used to derive, and obtain the time dependent version of the Ginzburg-Landau (GL) equation [3] . This topic will be treated separately.
For a many-fermion system, fermion field operators 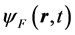 and
and![]() , satisfying the Fermi anticommutaion rules are introduced. The field equation is given by
, satisfying the Fermi anticommutaion rules are introduced. The field equation is given by
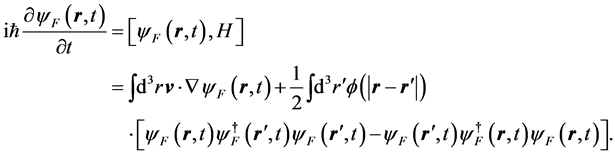 (39)
(39)
This equation is also nonlinear in the presence of a pair potential![]() .
.
References
- Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, Oxford Univ. Press, Oxford, 89-94; 121-125; 130-136; 136-139; 207-211; 227-237; 248-252.
- Debye, P. (1972) Annalen der Physik, 39, 789-839.
- Ginzburg, V.L. and Landau, L.D. (1950) Zh. Eksp. Teor. Fiz., 20, 1064-1082. [English translation in: L. D. Landau, “Collected papers,” Oxford: Pergamon Press (1965), 546.]

