Journal of Modern Physics
Vol.5 No.3(2014), Article ID:42658,4 pages DOI:10.4236/jmp.2014.53017
1Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan
2Department of Mathematics and Statistics, University of Victoria, Victoria, Canada
Email: *mawais@uvic.ca
Copyright © 2014 M. Ali, M. Awais. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property M. Ali, M. Awais. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 10, 2013; revised December 13, 2013; accepted January 8, 2014
ABSTRACT
In this article, we have effectively used the Numerical Inversion of Laplace transform to study the time-dependent thin film flow of a second grade fluid flowing down an inclined plane through a porous medium. The solution to the governing equation is obtained by using the standard Laplace transform. However, to transform the obtained solutions from Laplace space back to the original space, we have used the Numerical Inversion of Laplace transform. Graphical results have been presented to show the effects of different parameters involved and to show how the fluid flow evolves with time.
Keywords: Numerical Inversion of Laplace Transform; Unsteady Thin Film; Second Grade Fluid
1. Introduction
Laplace transform is a very useful tool for solving the differential equations. However, to analytically compute the inverse Laplace transform of the solutions obtained by the use of Laplace transform is a very important but complicated step. To overcome this issue, several algorithms for numerical inversion of Laplace transform have been proposed in literature [1-4]. Here we implement the idea of numerical inversion of Laplace transform presented by Weeks [1] and the one by Juraj and Lubomir [2].
The inverse Laplace transform 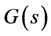 of a function
of a function 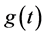 is given by the following contour integral
is given by the following contour integral
 (1)
(1)
Here  and
and ![]() is greater than the real part of any singularity in the transformed function G(s). Weeks method [1] for numerical inversion of Laplce transform is based on the use of the Laguerre functions and is given as
is greater than the real part of any singularity in the transformed function G(s). Weeks method [1] for numerical inversion of Laplce transform is based on the use of the Laguerre functions and is given as
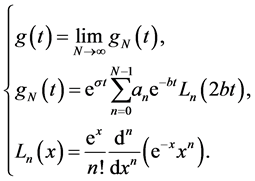
Whereas, the method of Juraj and Lumboir [2] is based on the use of infinite series for  and
and  along with the application of residue theorems to compute the contour integral given in (1). It gives us the following expression, which is also implemented here, for the numerical inversion of Laplace transform
along with the application of residue theorems to compute the contour integral given in (1). It gives us the following expression, which is also implemented here, for the numerical inversion of Laplace transform

Non-Newtonian fluids have been a famous topic of research because of their diverse use in many industrial processes. Various complex fluids such as oils, polymer melts, different types of drilling muds and clay coatings and many emulsions are included in the category of non-Newtonian fluids. One of the very important models suggested for non-Newtonian fluids is called the secondgrade fluid. Flows of second grade fluid have been studied by many [5-9]. Also, the flow of thin films has vast applications in industry. Such flows have applications in microchip productions, in biology, in chemistry and many other fields. Very often, thin film flows are examined by using steady flows. Some investigators have recently obtained some results for thin film flows of nonNewtonian fluids [10-14]. An investigation of thin film flow of a second order fluid is made by Huang and Li [15]. Miladinova et al. [11] studied the thin film flow of a power law fluid falling down an inclined plane and found a numerical solution. Analysis of lubrication flow of an upper-convected Maxwell fluid was carried out by Zhang and Li [12]. The field equation of micropolar fluids has been studied by Gan and Ji [16]. Siddiqui et al. [13,14] investigated thin film flow of non-Newtonian fluids by using the homotopy perturbation method. Linear and nonlinear stability analysis of the thin micropolar film flowing down a rotating cylinder was made by Chen [17]. M. Awais and S. Nadeem [18-20] investigated solutions for thin film flow of non-Newtonian fluids using a homotopy analysis method. However, studying unsteady thin film flow problems has always been a difficult and challenging task. Here, we solve an unsteady thin film flow problem of a second grade fluid by using the Laplace transform and then implement the methods of numerical inversion of Laplace transform described earlier to obtain the solutions in the original space and to find the effects of different fluid parameters. It also helps us to better understand the evolution of the flow with time.
2. Basic Equations
The momentum balance equation in the presence of a body force  and the equation of conservation of mass are respectively given as
and the equation of conservation of mass are respectively given as
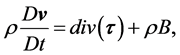 (2)
(2)
 (3)
(3)
with 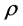 being the density,
being the density, ![]() the velocity,
the velocity, ![]() the stress tensor and
the stress tensor and 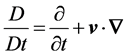 represents the material derivative. The stress tensor
represents the material derivative. The stress tensor ![]() in Equation (2) for a second grade fluid has form
in Equation (2) for a second grade fluid has form
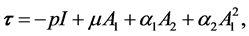 (4)
(4)
where 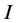 is the identity tensor,
is the identity tensor, ![]() is the pressure,
is the pressure, 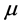 is the dynamic viscosity,
is the dynamic viscosity, 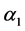 is the elastic coefficient and
is the elastic coefficient and 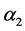 is the transverse viscosity coefficient and
is the transverse viscosity coefficient and 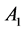 and
and 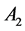 represent the Rivlin-Ericksen tensors. The tensors
represent the Rivlin-Ericksen tensors. The tensors 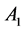 and
and 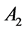 are defined by the following expressions
are defined by the following expressions
 (5)
(5)
 (6)
(6)
The material constants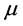 ,
,  and
and  also satisfy
also satisfy
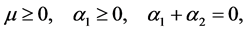 (7)
(7)
due to Clausius-Duhem inequality and the condition that the Helmholtz free energy is minimum when the fluid is at rest [21].
3. Governing Equations
We consider an unsteady gravity driven thin film flow of a second grade fluid of uniform film thickness ![]() flowing over a semi-infinite plate, inclined at an angle
flowing over a semi-infinite plate, inclined at an angle 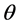 with the horizontal, through a porous medium, with stationary ambient air and negligible surface tension. The velocity field thus becomes
with the horizontal, through a porous medium, with stationary ambient air and negligible surface tension. The velocity field thus becomes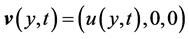 . Using such a velocity field in Equations (2)-(7) yields the following governing equation
. Using such a velocity field in Equations (2)-(7) yields the following governing equation
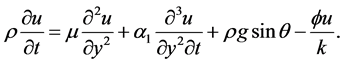 (8)
(8)
Symbols 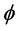 and
and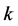 , respectively, represent the porosity and permeability of the porous space. The associated boundary conditions are
, respectively, represent the porosity and permeability of the porous space. The associated boundary conditions are
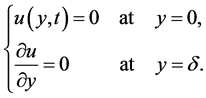 (9)
(9)
Here we would like to point out the presence of  in Equation (8). For time independent velocity field, the presence of the fluid parameter
in Equation (8). For time independent velocity field, the presence of the fluid parameter 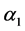 is completely wiped out from the governing equation. The first boundary condition in Equation (9) is due to the no-slip assumption at the boundary
is completely wiped out from the governing equation. The first boundary condition in Equation (9) is due to the no-slip assumption at the boundary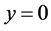 . Now considering the following nondimensional variables
. Now considering the following nondimensional variables
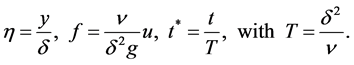 (10)
(10)
This gives us the following
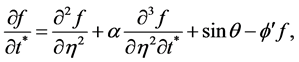 (11)
(11)
where 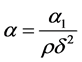 and
and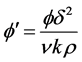 . The boundary conditions take the form
. The boundary conditions take the form
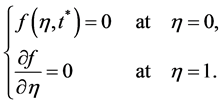 (12)
(12)
Taking the Laplace transform of Equations (11)-(12), we get, after rearranging
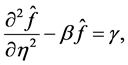 (13)
(13)
with  and
and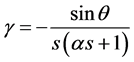 . Also, the transformed boundary conditions are
. Also, the transformed boundary conditions are
 (14)
(14)
Equations (13)-(14) have the following solution in the Laplace space
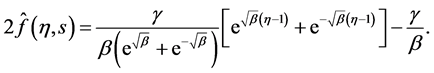 (15)
(15)
Now we use the method of numerical inversion of the Laplace transform [1,2] for the solution given in Equation (15) to give us the following plots.
4. Results and Discussion
The dimensionless velocity field for an unsteady thin film flow of a second grade fluid is plotted in Figure 1. The values of different parameters used are 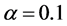 and
and  It is evident from these graphical results that the fluid velocity increases as the time progresses. Figure 2 provides us with the behaviour of the velocity profile due to changing
It is evident from these graphical results that the fluid velocity increases as the time progresses. Figure 2 provides us with the behaviour of the velocity profile due to changing![]() . The values of different parameters involved are
. The values of different parameters involved are 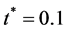 and
and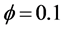 . A drop in the value of velocity is observed due to an increase of
. A drop in the value of velocity is observed due to an increase of![]() .
.
Figure 3, which depicts the change in velocity profile,  and
and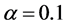 , due to changing porosity also shows a decrease in velocity for an increase in
, due to changing porosity also shows a decrease in velocity for an increase in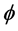 .
.
5. Conclusion
We have shown an efficient application of the numerical inverse Laplace algorithms [1,2] to study an unsteady thin film flow problem of a second grade fluid which is flowing through a porous medium along an inclined plane. This shows that the numerical inversion of the Laplace transform is a very effective and useful technique. Many unsteady problems of fluid flows, which are very hard to solve otherwise, can be dealt easily by the use of the Laplace transform. To accurately convert the solutions back to the original space, we can make use of
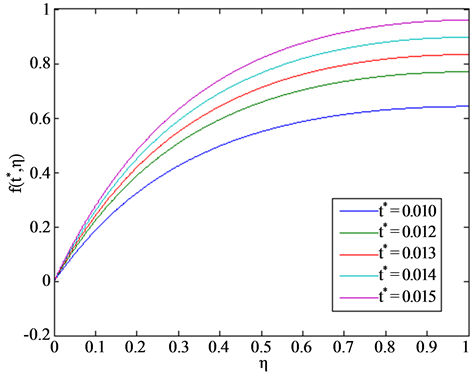
Figure 1. Plots for dimensionless velocity for different values of![]() .
.

Figure 2. Plots for dimensionless velocity for different values of![]() .
.

Figure 3. Plots for dimensionless velocity for different values of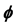 .
.
these efficient algorithms [1,2] available for the numerical inversion of the Laplace transform.
[1] REFERENCES
[2] W. T. Weeks, Journal of the ACM, Vol. 13, 1966, pp. 419-429. http://dx.doi.org/10.1145/321341.321351
[3] J. Valsa and L. Brancik, International Journal of Numerical Modelling, Vol. 11, 1998, pp. 153-166. http://dx.doi.org/10.1002/(SICI)1099-1204(199805/06)11:3<153::AID-JNM299>3.0.CO;2-C
[4] F. R. de Hoog, J. H. Knight and A. N. Stokes, SIAM Journal on Scientific Computing, Vol. 3, 1982, pp. 357-366.
[5] A. Talbot, Journal of Applied Mathematics, Vol. 23, 1979, pp. 97-120.
[6] B. Raftari, F. Parvaneh and K. Vajravelu, Energy, Vol. 59, 2013, pp. 625-632. http://dx.doi.org/10.1016/j.energy.2013.07.054
[7] Y. D. Yao and Y. H. Liu, Nonlinear Analysis: Real World Applications, Vol. 11, 2010, pp. 4442-4450. http://dx.doi.org/10.1016/j.nonrwa.2010.05.027
[8] M. E. Erdogan and C. E. Imrak, International Journal of Engineering Science, Vol. 48, 2010, pp. 1225-1232. http://dx.doi.org/10.1016/j.ijengsci.2010.06.007
[9] M. E. Erdogan and C. E. Imrak, International Journal of Non-Linear Mechanics, Vol. 46, 2011, pp. 986-989. http://dx.doi.org/10.1016/j.ijnonlinmec.2011.04.013
[10] M. E. Erdogan and C. E. Imrak, Applied Mathematical Modelling, Vol. 31, 2007, pp. 170-180. http://dx.doi.org/10.1016/j.apm.2005.08.019
[11] P. Huang and Z. Li, Journal of Tribology, Vol. 124, 2002, pp. 547-552. http://dx.doi.org/10.1115/1.1467636
[12] S. Miladinova, G. Lebon and E. Toshev, Journal of NonNewtonian Fluid Mechanics, Vol. 122, 2004, pp. 69-78. http://dx.doi.org/10.1016/j.jnnfm.2004.01.021
[13] R. Zhang and X. Li, Journal of Engineering Mathematics, Vol. 51, 2005, pp. 1-13. http://dx.doi.org/10.1007/s10665-004-1342-z
[14] A. M. Siddiqui, R. Mahmood and Q. K. Ghori, Physics Letters A, Vol. 352, 2006, pp. 404-410. http://dx.doi.org/10.1016/j.physleta.2005.12.033
[15] A. M. Siddiqui, M. Ahmed and Q. K. Ghori, Chaos Solitons Fractals, Vol. 33, 2007, pp. 1006-1016. http://dx.doi.org/10.1016/j.chaos.2006.01.101
[16] P. Huang and Z. Li, Journal of Tribology, Vol. 124, 2002, pp. 547-552. http://dx.doi.org/10.1115/1.1467636
[17] Q. Z. Gan and L. Z. Ji, Applied Mathematics and Mechanics, Vol. 8, 2006, pp. 655-665. http://dx.doi.org/10.1007/BF02458263
[18] C. I. Chen, Communications in Nonlinear Science and Numerical Simulation, Vol. 12, 2007, pp. 760-775. http://dx.doi.org/10.1016/j.cnsns.2005.04.010
[19] M. Sajid, M. Awais, S. Nadeem and T. Hayat, Computers and Mathematics with Applications, Vol. 56, 2008, pp. 2019-2026. http://dx.doi.org/10.1016/j.camwa.2008.04.022
[20] S. Nadeem and M. Awais, Physics Letters A, Vol. 372, 2008, pp. 4965-4972. http://dx.doi.org/10.1016/j.physleta.2008.05.048
[21] S. Nadeem and M. Awais, Journal of Porous Media, Vol. 13, 2010, pp. 973-980. http://dx.doi.org/10.1615/JPorMedia.v13.i11.30
[22] J. E. Dunn and R. L. Fosdick, Archive for Rational Mechanics and Analysis, Vol. 56, 1974, pp. 191-252. http://dx.doi.org/10.1007/BF00280970
NOTES
*Corresponding author.

