Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40501,6 pages DOI:10.4236/jmp.2013.412192
Ferromagnetism in Diluted Magnetic Semiconductor (Ga,Mn)As Quantum Wires and Quantum Wells under the Influence of Photo-Excitation and Spin Wave Scattering
1Physics Department, Addis Ababa Science and Technology University, Addis Ababa, Ethiopia
2Physics Department, Panjab University, Chandigarh, India
Email: chernetamente@gmail.com, keya@pu.ac.in
Copyright © 2013 Chernet Amente, Keya Dharamvir. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 7, 2013; revised September 12, 2013; accepted October 6, 2013
Keywords: Heat Capacity; Magnetization; Photo-Excitation; Quantum Wells; Quantum Wires; Spin Wave Scattering
ABSTRACT
We present a theoretical investigation of the influence of photo-excitation and spin wave scattering on magnetization of the (Ga,Mn)As diluted magnetic semiconductor (DMS) quantum wires (QWRs) and quantum wells (QWs). Double time temperature dependent Green’s function formalism is used for the description of dispersion and spectral density of the systems. Our analysis indicates that spin wave scattering plays an influential role in magnetism of both systems while application of light is insignificant in quantum wells. In the absence of spin wave scattering and at sufficiently low temperatures, a result corresponding to the specific heat of dominating electronic contributions in metals is obtained in QWs. In QWRs, however, this magnetic property is found to vary with 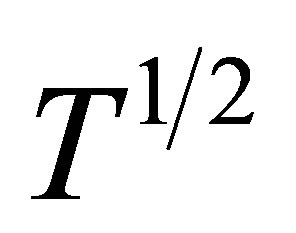 and
and  so that light matter coupling has a leading effect on lower temperatures, where α is the light matter coupling factor and T is the temperature.
so that light matter coupling has a leading effect on lower temperatures, where α is the light matter coupling factor and T is the temperature.
1. Introduction
The discovery of giant magnetoresistive (GMR) phenomena in the late 1980’s [1,2] was remarkable in its innovation which can be used as magnetoresistance sensor. It has led to the search for efficient and high density electronic devices with very large storage capability. This has aroused a lot of research interest in the study of diluted magnetic semiconductors (DMSs). Among these, (Ga,Mn)As is the most studied since GaAs is the most useful semiconductor, especially in producing optical devices due to its good optical properties and applications in which high speed is required [3]. Doping with magnetic impurities, such as Mn, Cr, Fe and so on, would give new features that include data processing and storage facilities in a single crystal. Mn is known to be advantageous as it produces a special quality introducing high density of magnetic moments and holes to the system. This is shown in Table 1 which presents comparison between few transition elements.
Being doped into III-V semiconductors, there is a valence mismatch between both Mn2+ 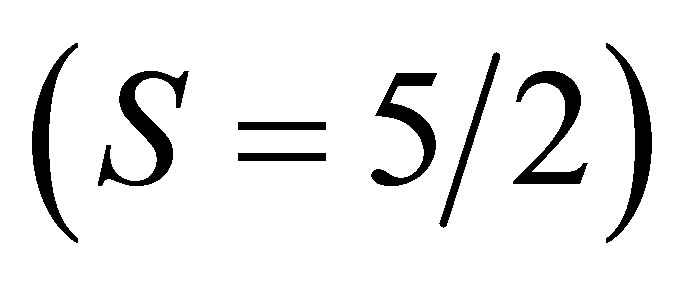 and the group-III elements. The 3d electrons contributed from Cr2+ doping would be less in number (4 per atom,
and the group-III elements. The 3d electrons contributed from Cr2+ doping would be less in number (4 per atom,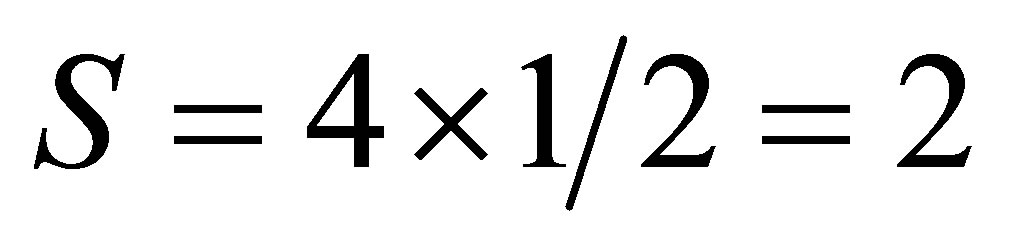 ) contributing less magnetic impurity spins per atom leading to weak magnetic ordering. In Fe2+ the 3d electrons would give rise to
) contributing less magnetic impurity spins per atom leading to weak magnetic ordering. In Fe2+ the 3d electrons would give rise to  similarly. Fe3+ matches in valence with group III element just as Mn2+ does in II-VI DMSs. The acceptor levels of Fe and Cr are, therefore, unlikely to lead to high valence band hole concentrations in Arsenides [4]. Hence, Mn2+ is essential for the doping purpose, so that the RKKY type indirect exchange interaction is created in the valence band [5].
similarly. Fe3+ matches in valence with group III element just as Mn2+ does in II-VI DMSs. The acceptor levels of Fe and Cr are, therefore, unlikely to lead to high valence band hole concentrations in Arsenides [4]. Hence, Mn2+ is essential for the doping purpose, so that the RKKY type indirect exchange interaction is created in the valence band [5].
However, room temperature functionality of (Ga,Mn)As based spintronic devices has not yet been realized due to inability of raising ferromagnetic transition temperature, TC, beyond the required. On the other hand, experimental study of photo induced DMSs show photo-excitation which might improve the situation circumventing the problem [6-8].
It has been explained that, in (Ga,Mn)As absorption occurs in the visible range in which light absorption can occur at sub-band-gap frequencies due to excitations
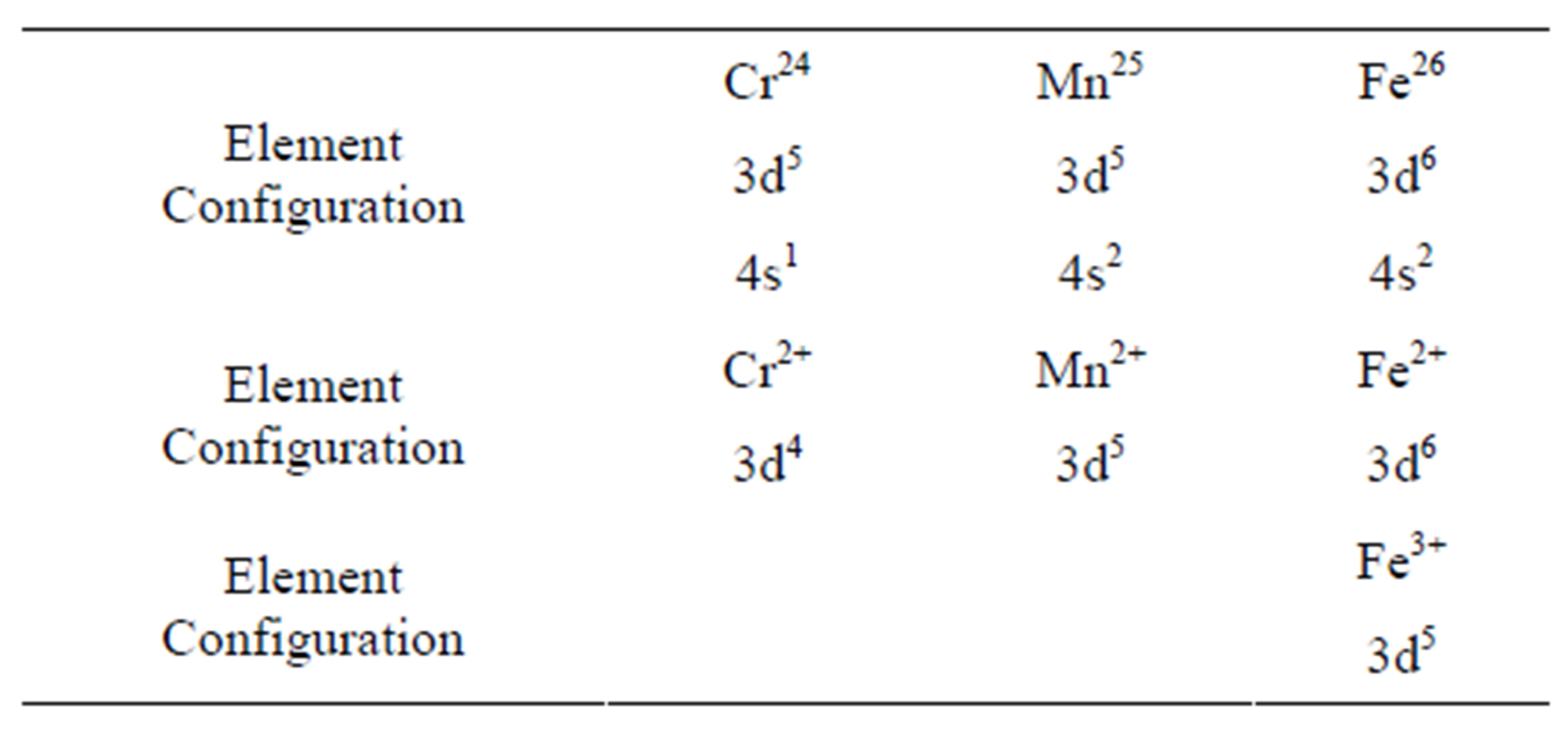
Table 1. The most commonly used magnetic elements for doping purpose in DMSs are shown.
from the valence band to the Mn impurity band in more insulating materials [9] and due to intra-valence-band excitations in more metallic systems [10]. Since the analysis of this magneto-optical effect provides information on the p-d exchange-induced band splitting and on doping in the DMS material [11], it would be an essential that extension of the study to the case of reduced dimensionality like quantum wire [12,13] and quantum well [14] in which confinement is achieved and gives further opportunity for the investigation of their magnetic properties presumably resulting in high spin wave density and high density of carriers required for mediation.
In the present work, influence of photo-excitation and magnon-scattering on ferromagnetism of the diluted magnetic semiconductor (Ga,Mn)As quantum wire and quantum well is studied. Starting with a standard model Hamiltonian [15], and using the method of double-time temperature dependent Green function [16], the average number of magnons are derived. Magnetization, ferromagnetic transition temperature TC, and specific heat, Cmag are obtained and compared with the available experimental results.
2. Formulation of the Problem
The model Hamiltonian used to describe the systems is expressed as
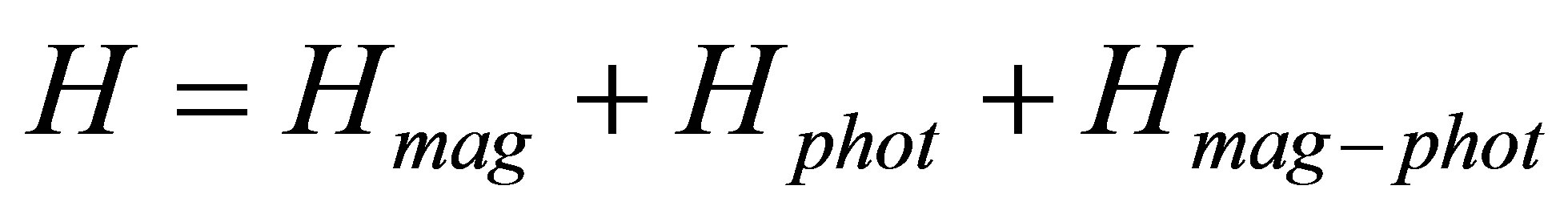 (1)
(1)
The total magnon energy, 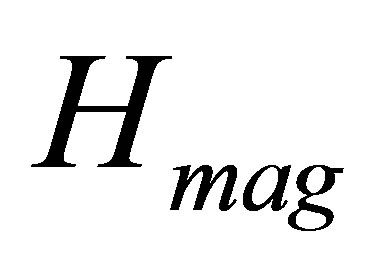 can be obtained from the Heisenberg direct exchange energy that Dietl [17] used in describing DMS systems in analogy with the Zeener indirect exchange [17-19] expressed by
can be obtained from the Heisenberg direct exchange energy that Dietl [17] used in describing DMS systems in analogy with the Zeener indirect exchange [17-19] expressed by
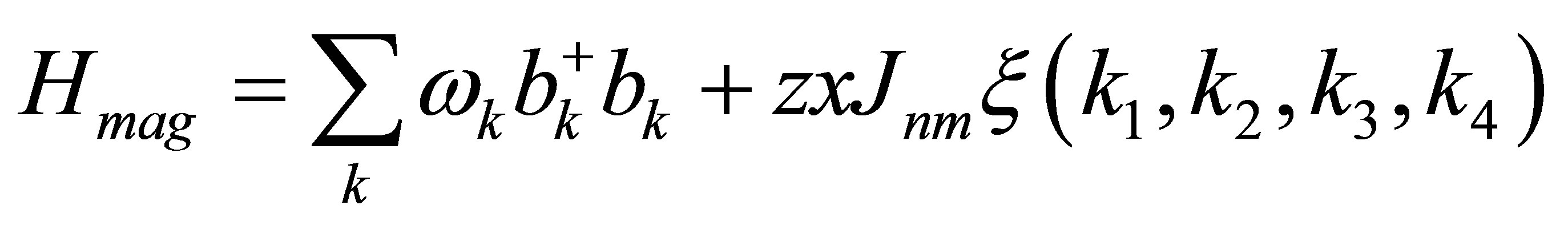 (2)
(2)
in which 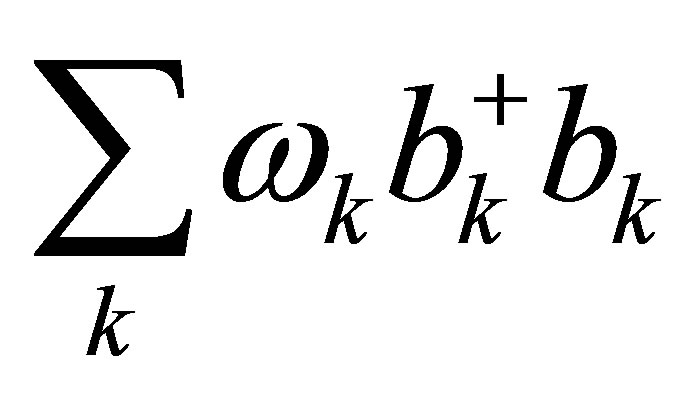 is for free magnon energy.
is for free magnon energy.
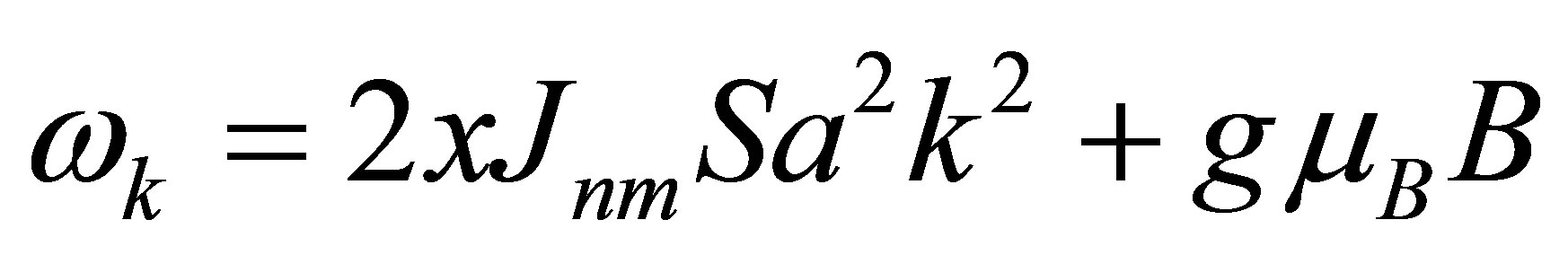 is the free magnon dispersion where Jnm is the energy exchange strength between spins localized at n and m presumed sites. S represents localized spins per atom, a the lattice constant of (Ga,Mn)As in view of that it would have as of GaAs in this context. k is the magnon wave vector, g the g-factor,
is the free magnon dispersion where Jnm is the energy exchange strength between spins localized at n and m presumed sites. S represents localized spins per atom, a the lattice constant of (Ga,Mn)As in view of that it would have as of GaAs in this context. k is the magnon wave vector, g the g-factor, 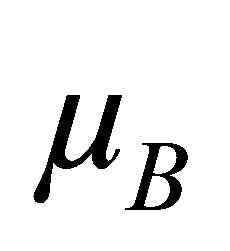 the Bohr magneton and B is magnitude of applied field.
the Bohr magneton and B is magnitude of applied field. 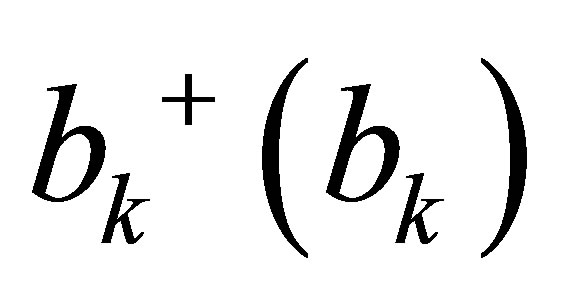 denotes the magnon creation (annihilation) operator, and
denotes the magnon creation (annihilation) operator, and 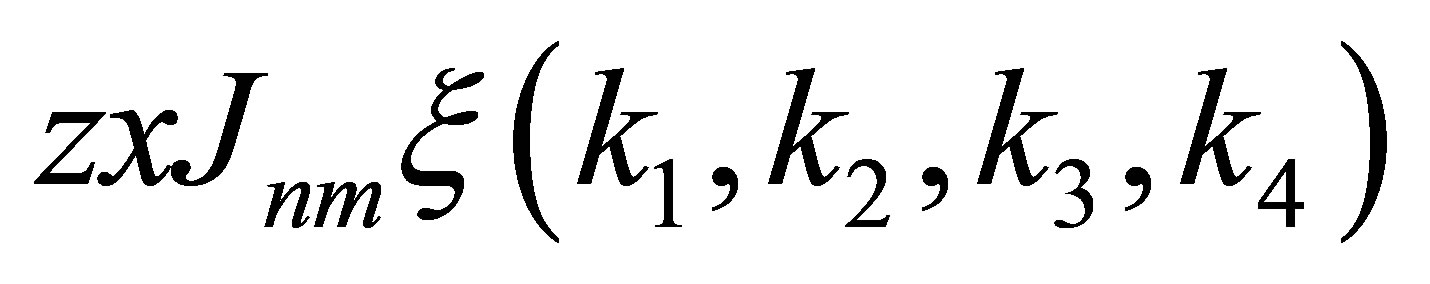 represents magnon scattering energy[15, 20] where x is the magnetic impurity concentration [19].
represents magnon scattering energy[15, 20] where x is the magnetic impurity concentration [19].
Using Holstein-Primakoff (HP) bosons [21] and coarse graining the spin density Sn (spin at site n) can be written as, 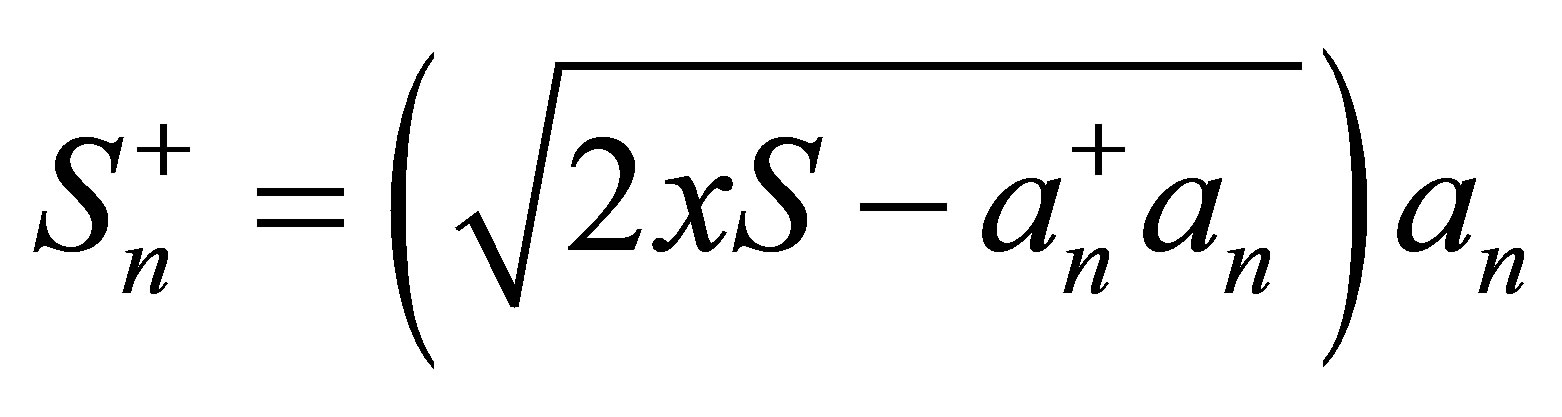 ,
, 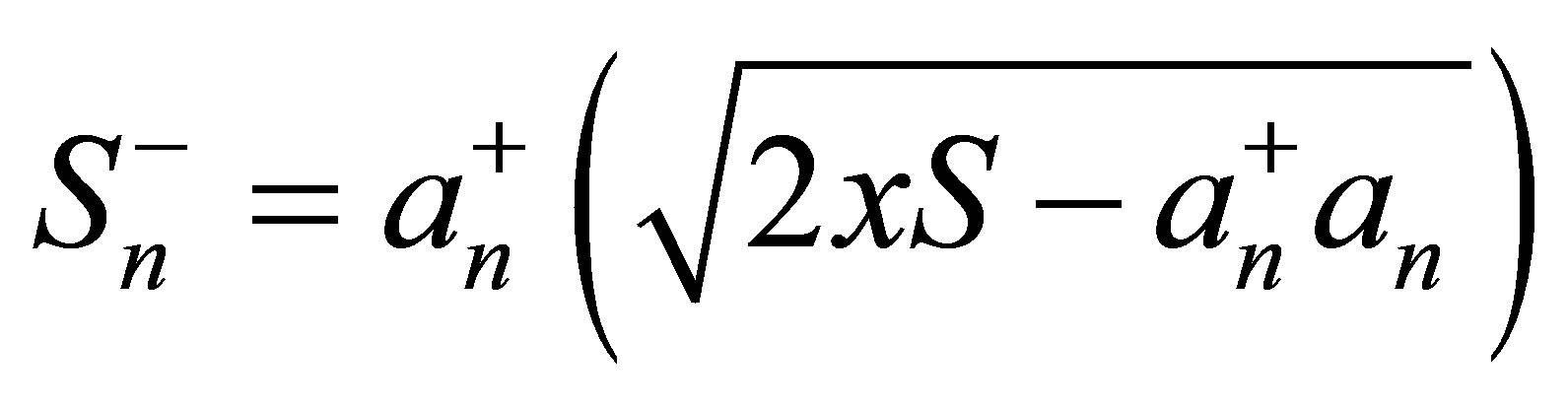 and
and
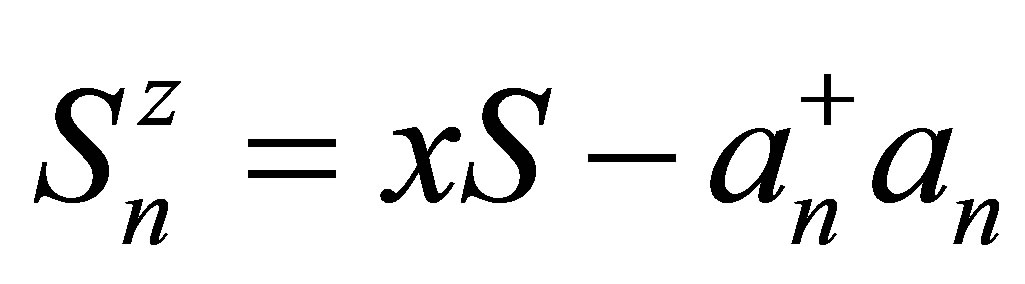 . Because of spin wave propagation throughout the system, Fourier variables
. Because of spin wave propagation throughout the system, Fourier variables
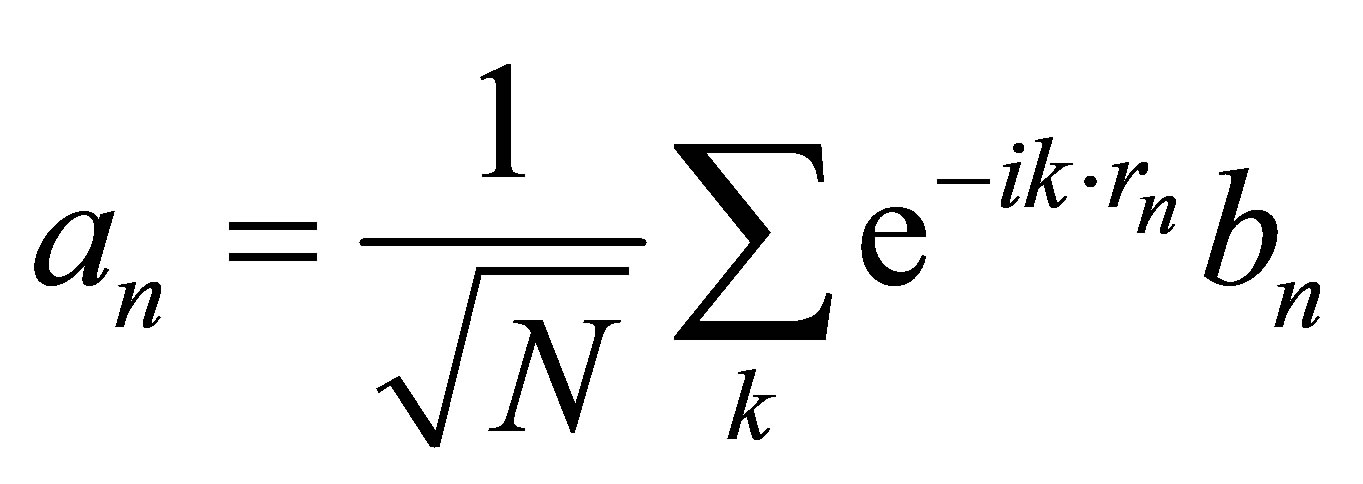 , and
, and 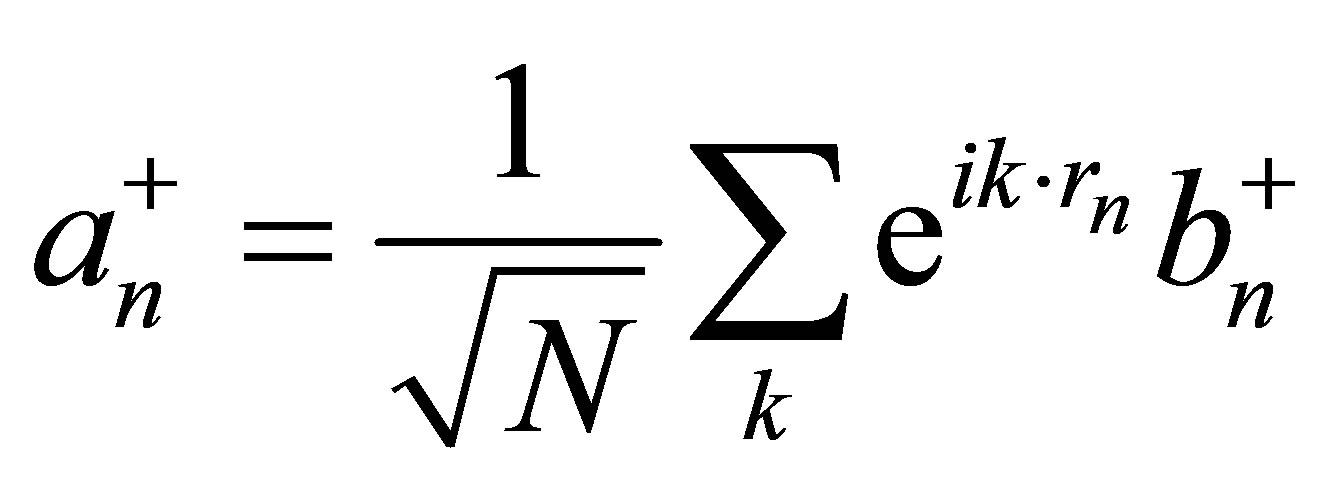 are considered where the bosonic
are considered where the bosonic 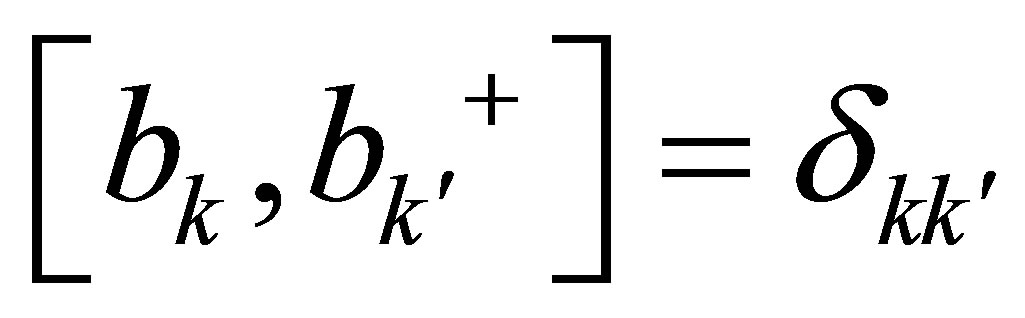 is also satisfied.
is also satisfied.
The second term in the right hand side of Equation (1),
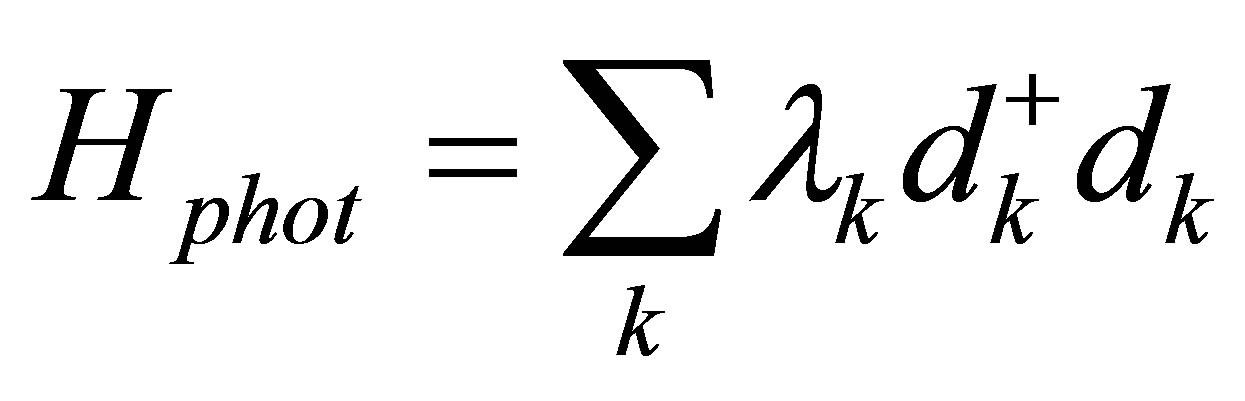 represents free photon energy, where
represents free photon energy, where
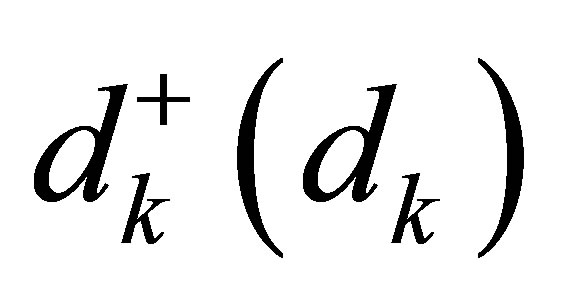 is photon creation (annihilation) operator,
is photon creation (annihilation) operator, 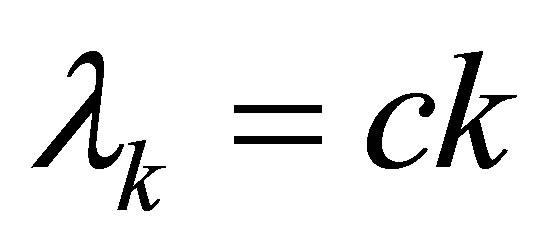 is dispersion of photon and c is speed of light in free space.
is dispersion of photon and c is speed of light in free space.
The third term in the right hand side of Equation (1),
 represents the magnon-photon interaction energy, in which
represents the magnon-photon interaction energy, in which 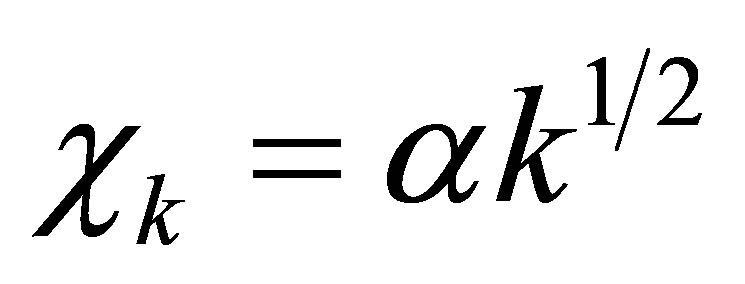 and
and
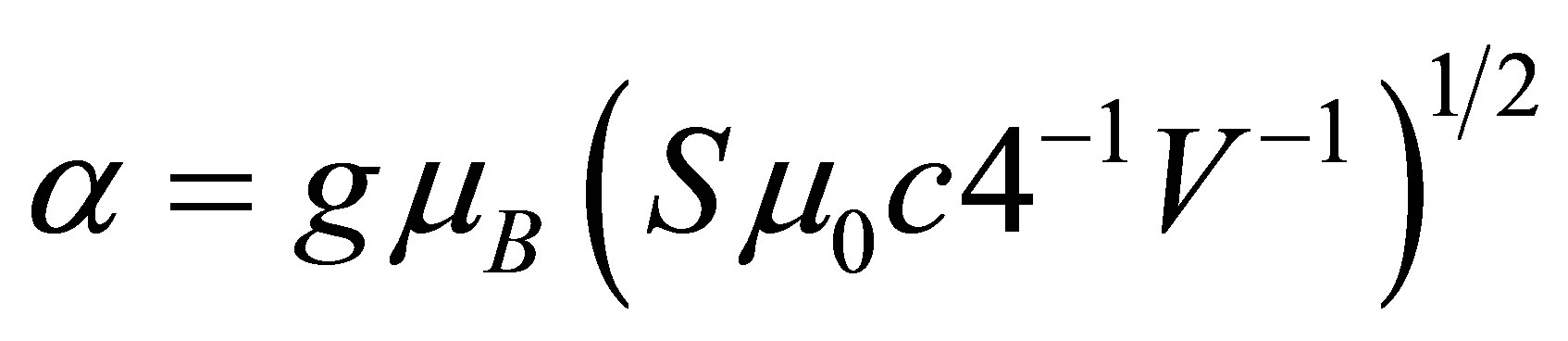 ,
,  permeability of free space, and V volume of the radiation field cavity.
permeability of free space, and V volume of the radiation field cavity.
3. Magnetization and the Ferromagnetic Transition
Magnetism of Mn doped GaAs QWRs and QWs have been studied for decades [12-14,22,23]. Experimental observations indicate that a magnetization curve as a function of magnetic field at 5 K and room temperature ferromagnetic transition temperature are obtained for QWRs [22]. QWs, on the other hand, have been utilized in electronic devices through band gap engineering since their realization [23] and are an interesting subject of study currently. In this paper, the magnetic aspect of these systems are theoretically investigated by analytical method. It is presumed that nano systems can be recasted from the bulk and the basic structure remains similar except that the atoms on surface are larger in the former.
The total number of magnons for these systems would be described by 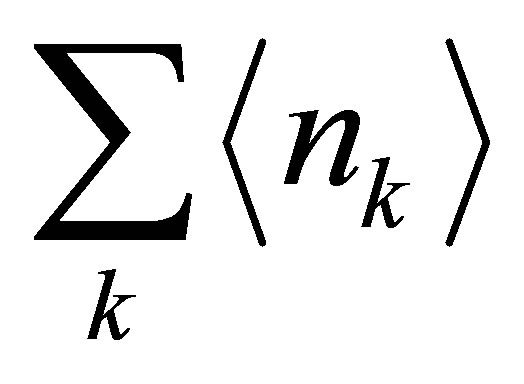 , where
, where
 (3)
(3)
And can be obtained from the calculation of spectral density, in which 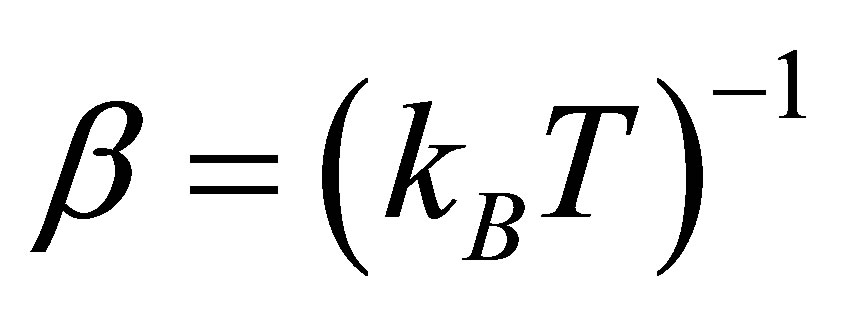 and
and 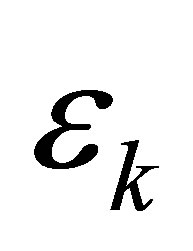 [15] is the over all magnon dispersion obtained from the equation of motion:
[15] is the over all magnon dispersion obtained from the equation of motion:
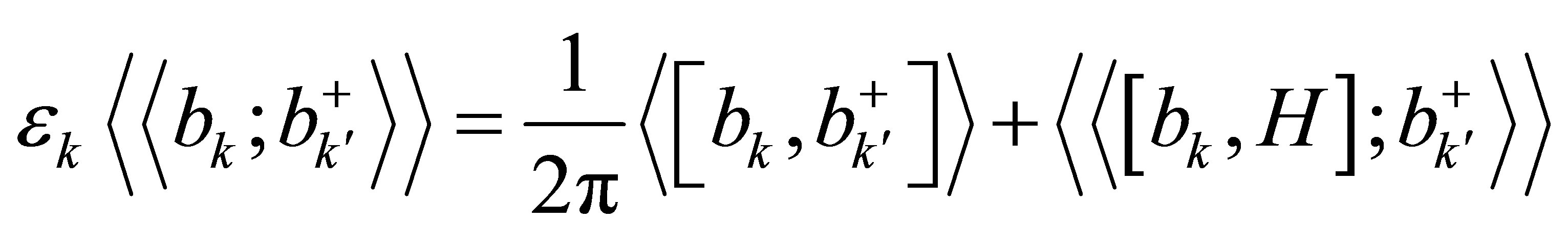 (4)
(4)
after substituting Equation (1) into (4), where  is abbreviated notation (Fourier transform) for the Green function. The square brackets […] denote a commutator, and single-pointed brackets
is abbreviated notation (Fourier transform) for the Green function. The square brackets […] denote a commutator, and single-pointed brackets  a thermal average over a canonical ensemble which is appropriate since the number of particles is not constant.
a thermal average over a canonical ensemble which is appropriate since the number of particles is not constant.
3.1. Magnetization of the Quantum Wire
In view of the fact that quantum wires are structures confined from two sides conversion of the summation into integration gives total number of magnons expressed as
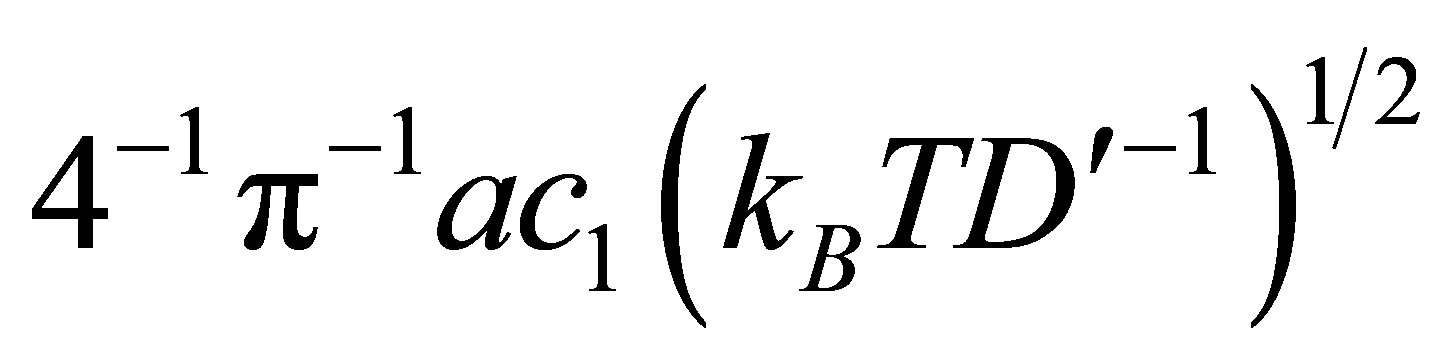 and
and 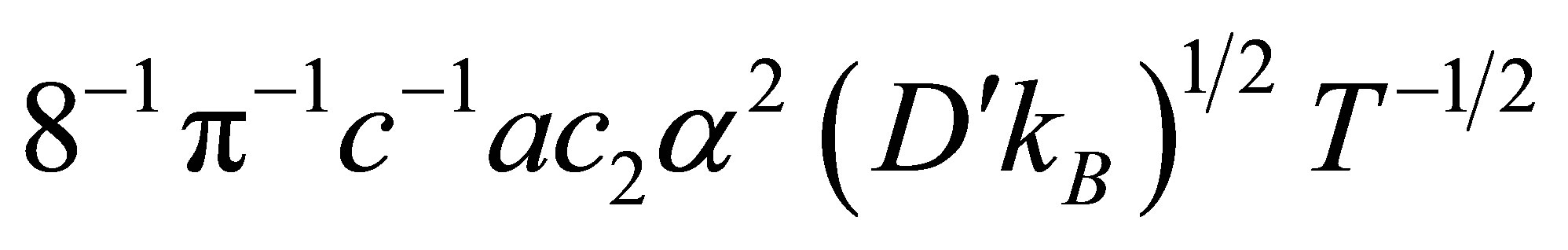
at higher and lower temperature limits, respectively, where  and
and 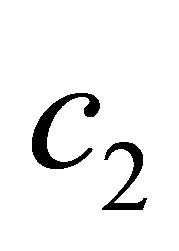 are constants.
are constants. 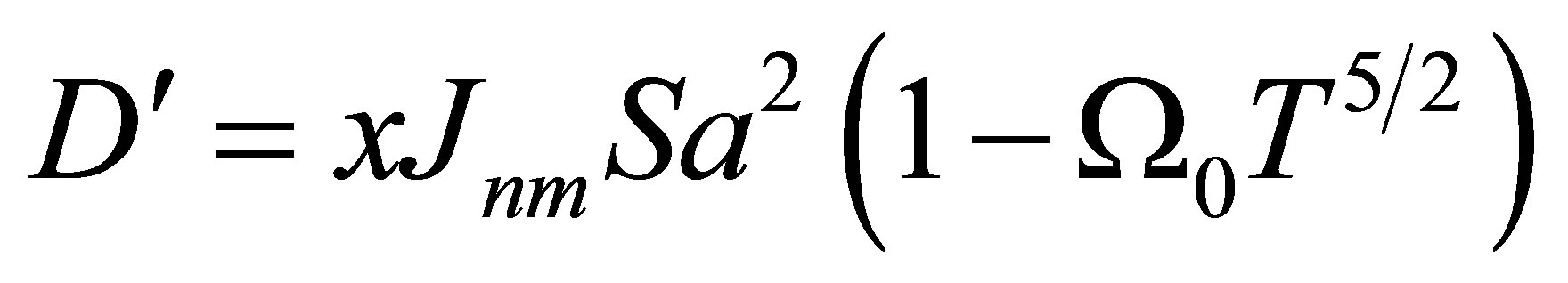 and
and 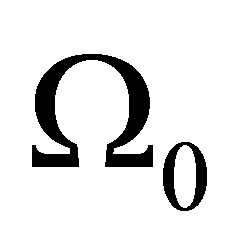 and its significance was explained in the past [15].
and its significance was explained in the past [15].
Using the famous Bloch relation and Equation (2), reduced magnetization, m(T) can be written for sufficiently low and high temperatures as  and
and 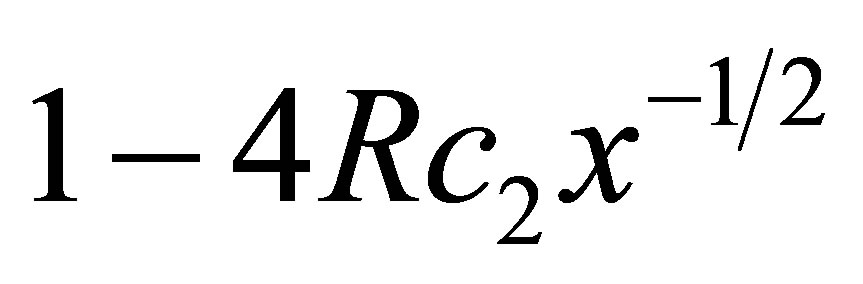 , respectively, where
, respectively, where
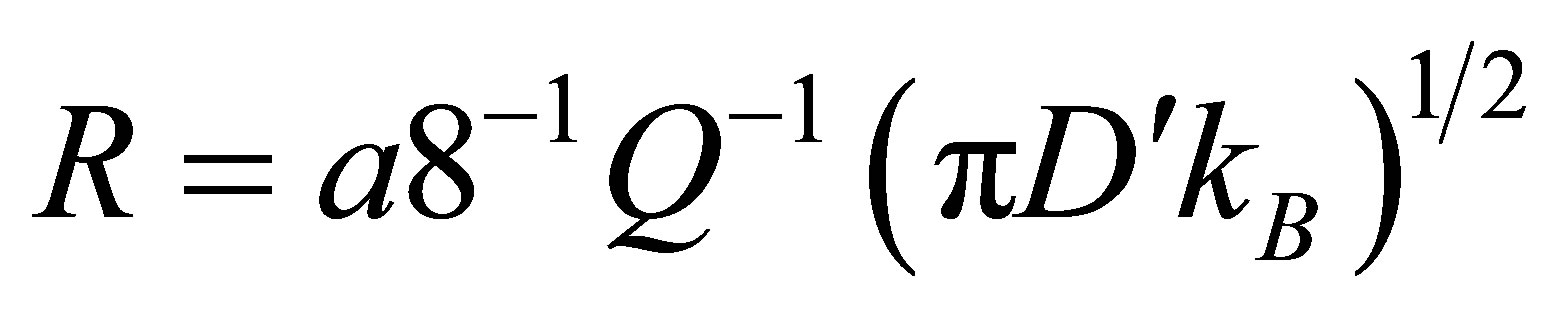 and
and 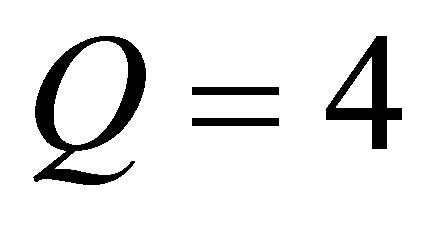 for fcc lattices.
for fcc lattices.
Figures 1 and 2 demonstrate the raising of magnetization with temperature at lower temperature limit, where effect of spin wave scattering is insignificant. The magnetization has a tendency of decreasing as temperature goes far below 1 K leading to negative value near 0K. According to further analysis, however, there is a slight improvement with increase in impurity concentration and light irradiation. At higher temperatures our calculations does not show any effect of light irradiation on ferromagnetic transition temperature, TC and the magnetization, m(T). The magnetization is also getting decrease with increasing temperature forming a concave behaviour at a start (see Figure 1). This could be due to a combination of the strongly localized nature of the carrier system and low values of the carrier density in the DMS material [24]. Moreover, magnon scattering is also shown to be the other factor that would have impact on Tc and m(T) of the system. Figures 3 and 4 show that at lower temperatures TC becomes decreasing with increasing x and also depends on magnon-photon coupling strength. The scrutiny of Figure 3 shows that the sudden drop of TC is limited to very close 0 K as light matter coupling factor decreases further. This suggests that there can be disorder because of the required number of holes is much lower than the amount of localized spins leading to anomalous condition. At higher temperature limits, however, the usual 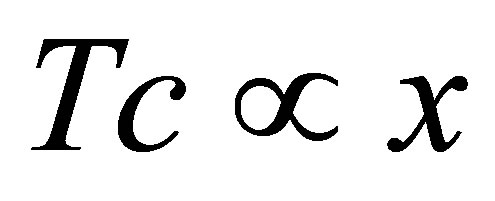 relation is maintained regardless of the spin wave scattering.
relation is maintained regardless of the spin wave scattering.
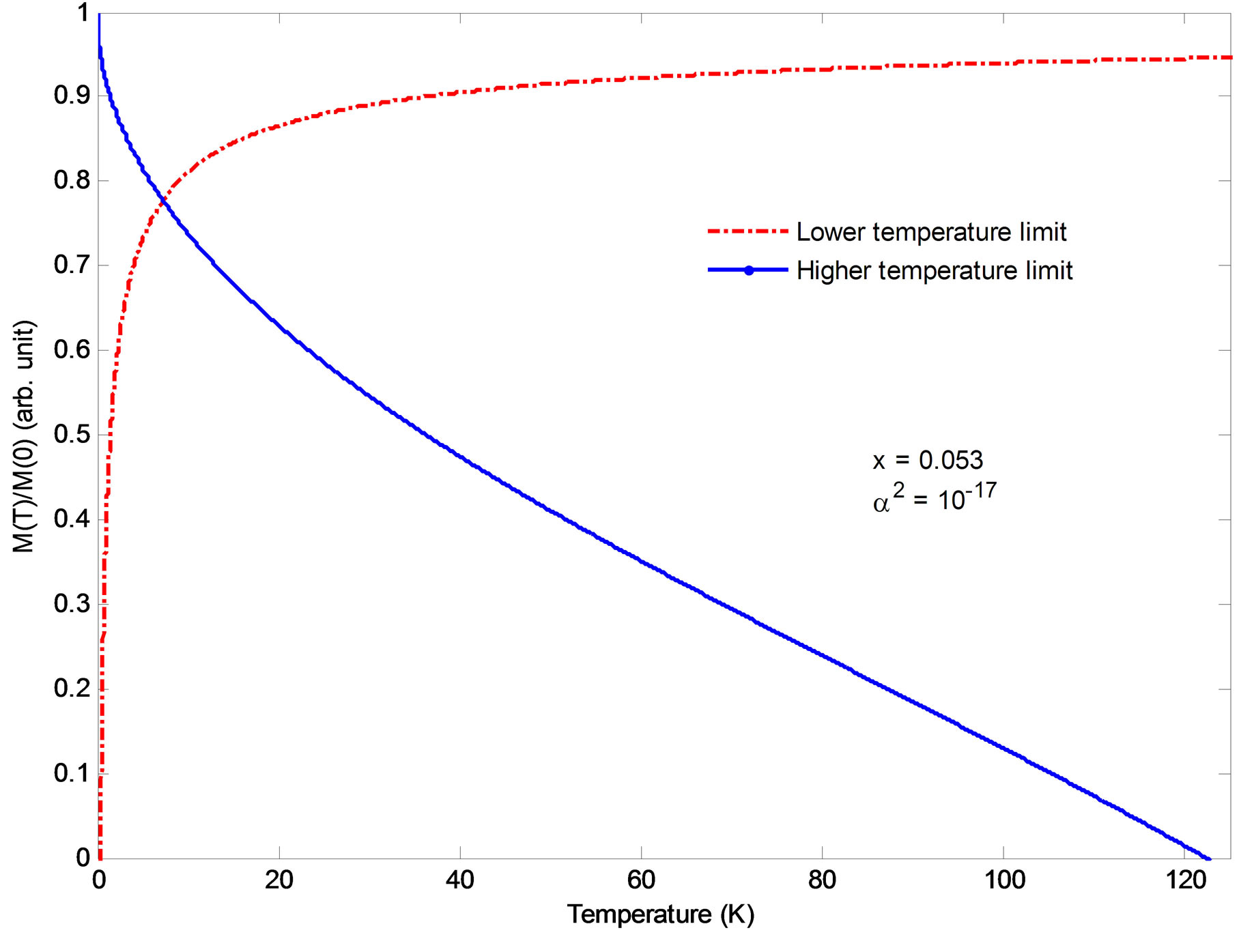
Figure 1. (Color online) Magnetization m(T) vs. temperature in a QWR, at lower and higher temperature limits for x = 0.053.
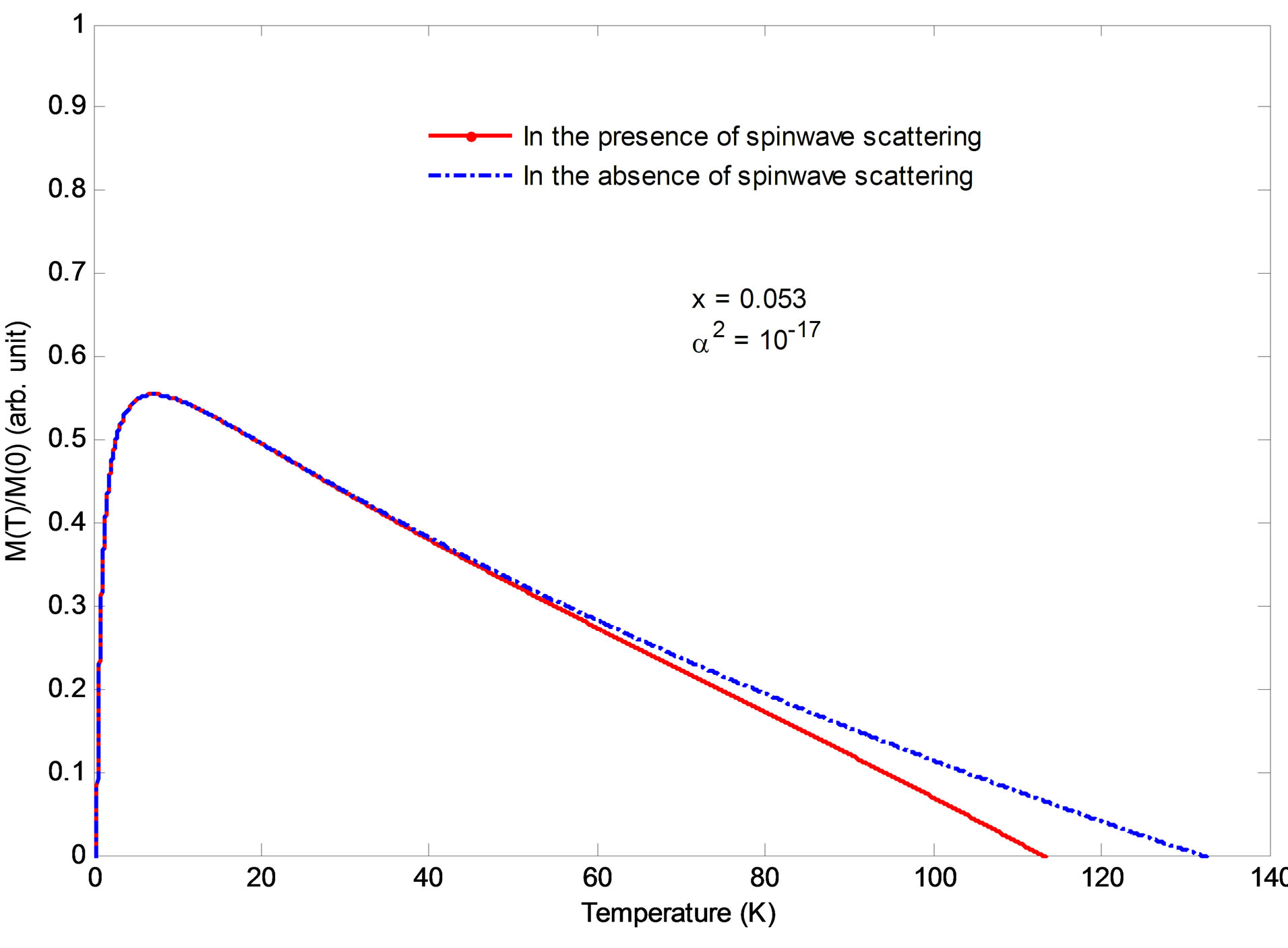
Figure 2. (Color online) Low and high temperature limits combined effect on Magnetization m(T) in a QWR at x = 0.053.

Figure 3. (Color online) Ferromagnetic transition temperature vs. magnetic impurity concentration a QWR at lower and higher temperatures.
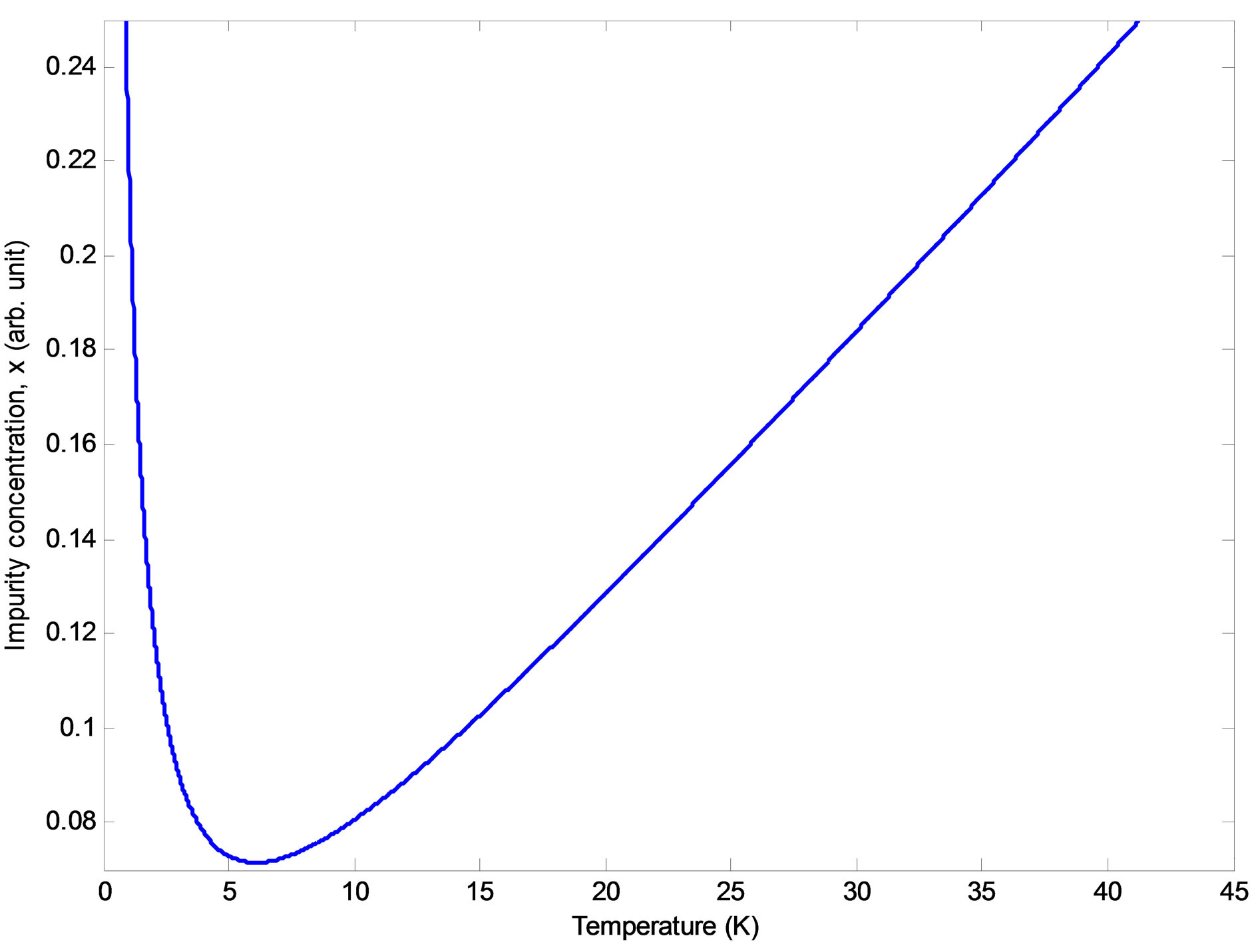
Figure 4. (Color online) High and low temperature combined effect on Ferromagnetic transition temperature of the QWR.
3.2. Magnetization of the Quantum Well
The total number of magnons in the system can be shown to be 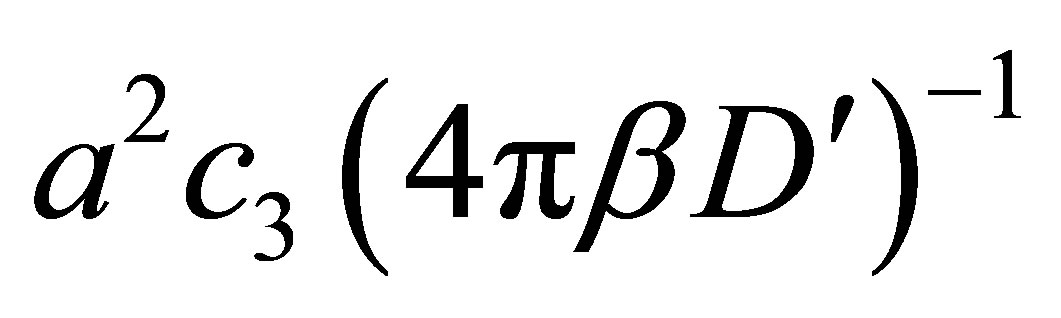 from which magnetization can be found as
from which magnetization can be found as 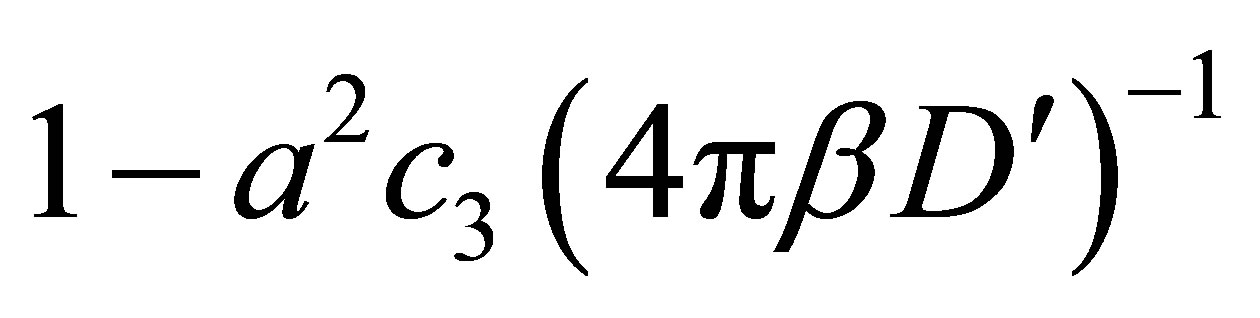 where
where  is a constant. Figure 5 illustrats that the quantum well magnetization could, therefore, be affected by the magnetic impurity concentration and strength of exchange energy at lower temperature region at large. Hence, the ferromagnetic transition temperature would be obtained as
is a constant. Figure 5 illustrats that the quantum well magnetization could, therefore, be affected by the magnetic impurity concentration and strength of exchange energy at lower temperature region at large. Hence, the ferromagnetic transition temperature would be obtained as 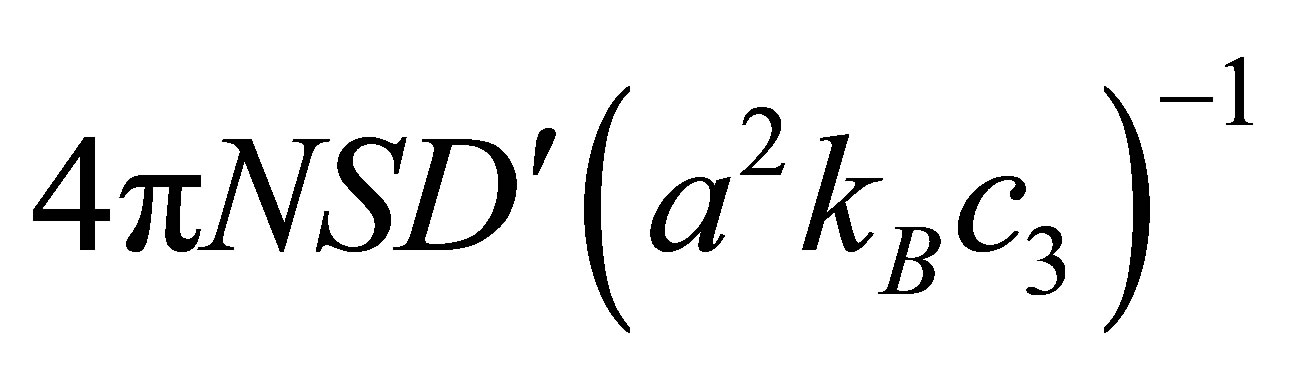 which in the absence of spin wave scattering becomes
which in the absence of spin wave scattering becomes  . This demonistrates that spin wave scattering could have altered the ferromagnetic transition temperature, TC, specially, at higher impurity concentration, as can be revealed from Figure 6 as well.
. This demonistrates that spin wave scattering could have altered the ferromagnetic transition temperature, TC, specially, at higher impurity concentration, as can be revealed from Figure 6 as well.
Shape of the untypical 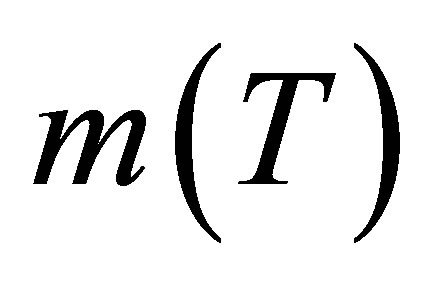 curve in Figure 5 is, suggested as, due to the interactions between magnetic systems (Ga,Mn)As and MnAs layers [25]. A similar result is obtained by Jung et al., 2007, in which magnetization shows decaying behaviour rather than an abrupt transition [26].
curve in Figure 5 is, suggested as, due to the interactions between magnetic systems (Ga,Mn)As and MnAs layers [25]. A similar result is obtained by Jung et al., 2007, in which magnetization shows decaying behaviour rather than an abrupt transition [26].
4. The Magnon Specific Heat Capacity
The expression for specific heat, Cmag of the diluted magnetic semiconductor systems would be obtained from internal energy of magnons, 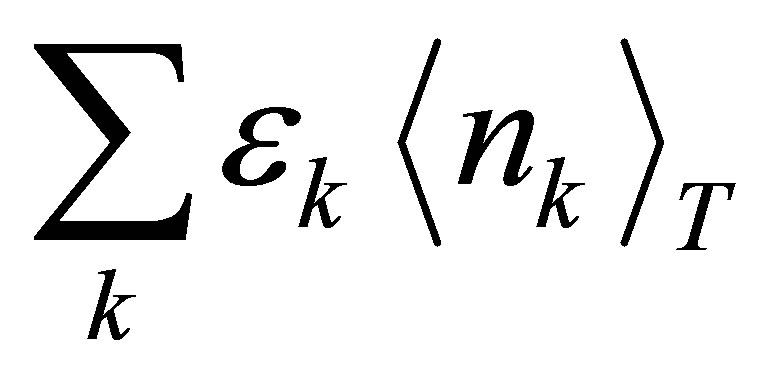 .
.
4.1. Specific Heat of the Quantum Wire
For (Ga,Mn)As quantum wires, specific heat can be shown to be  and
and 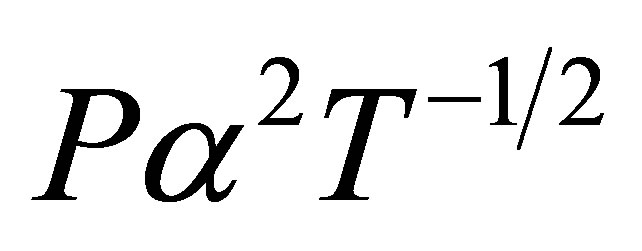 at high and low temperatures, respectively, where
at high and low temperatures, respectively, where 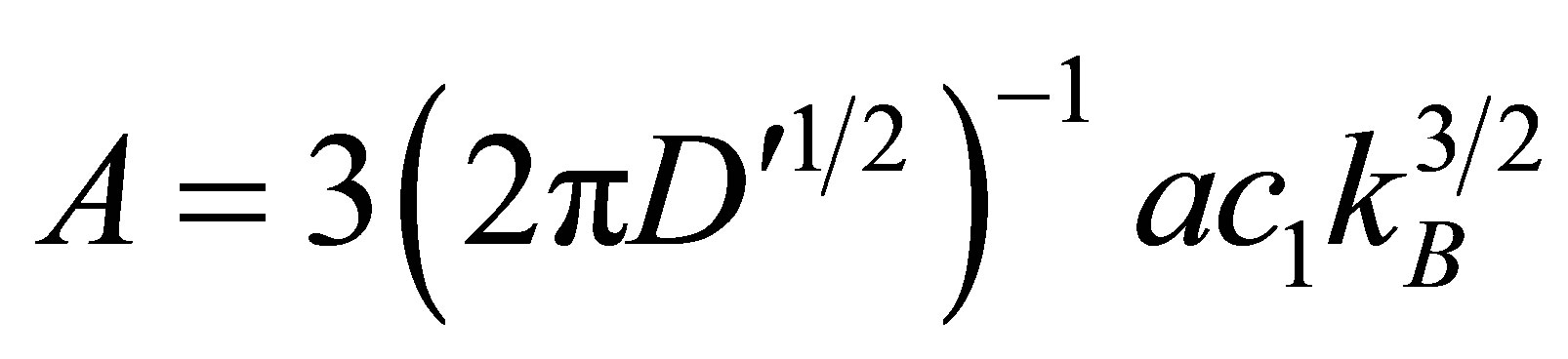
and 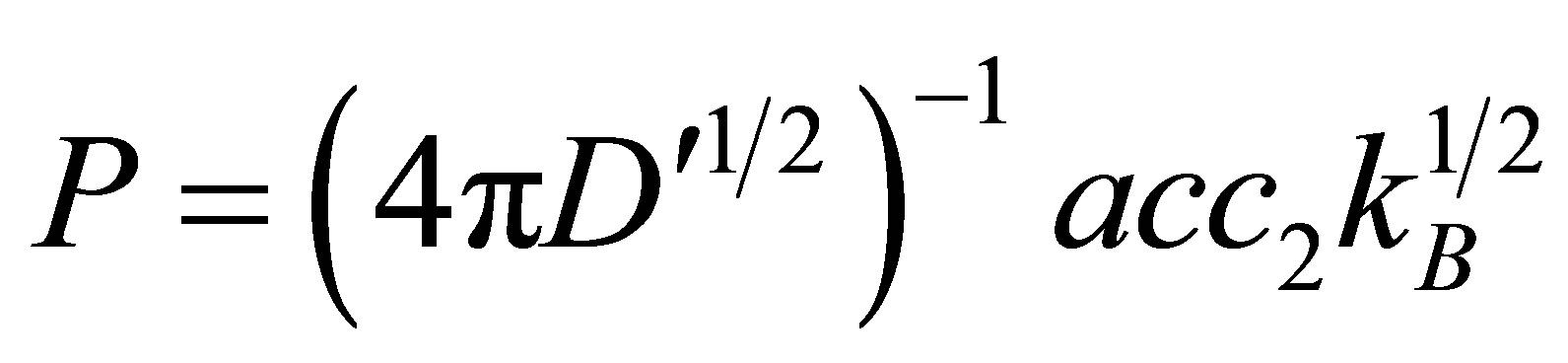 indicating that low temperature limits are eminently affected by light-matter coupling strength. Figure 7 shows that at higher tem-
indicating that low temperature limits are eminently affected by light-matter coupling strength. Figure 7 shows that at higher tem-
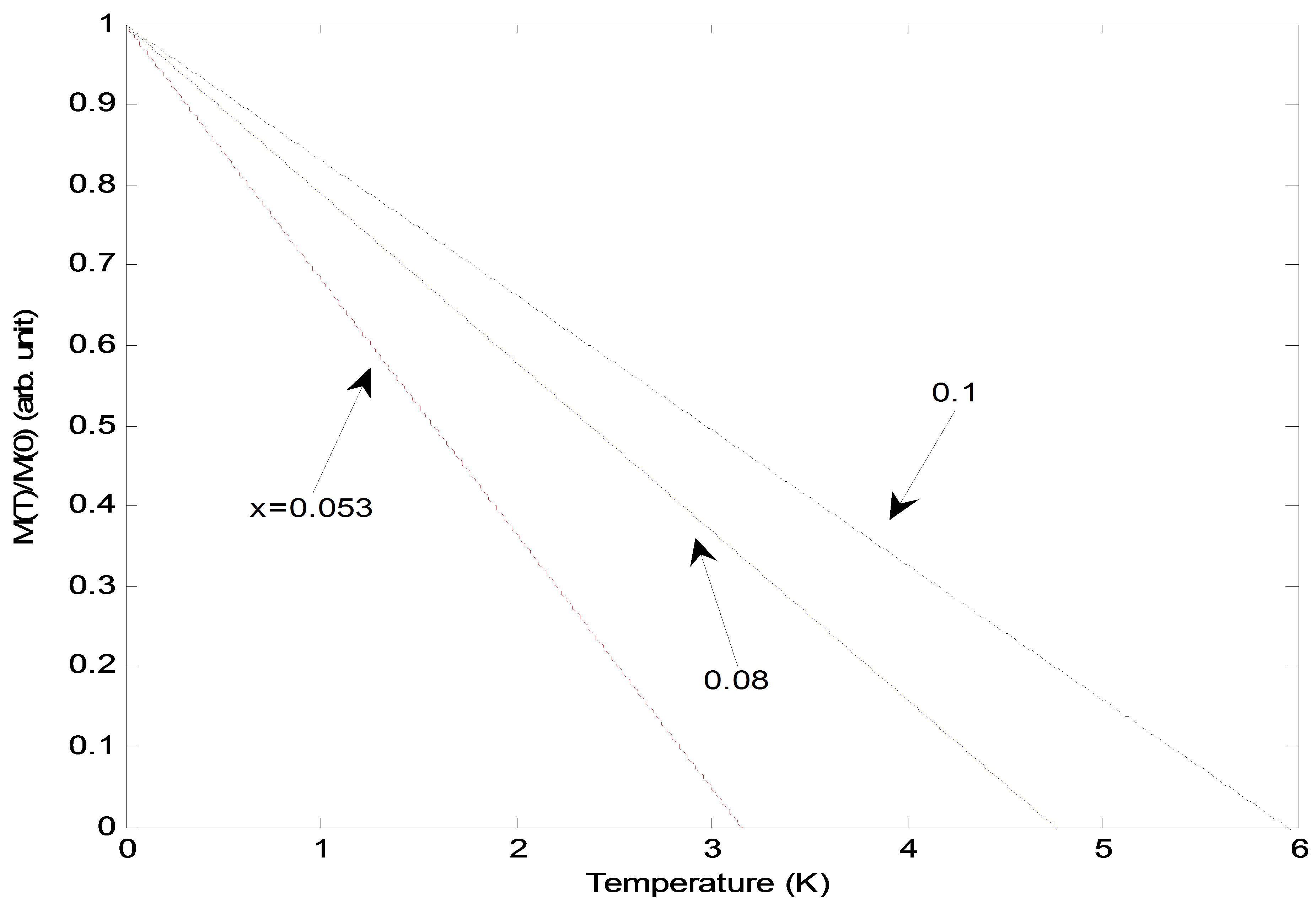
Figure 5. (Colour online) Magnetization, m(T) vs. temperature, T for a QW in the presence of spin wave scattering for different impurity concentrations.
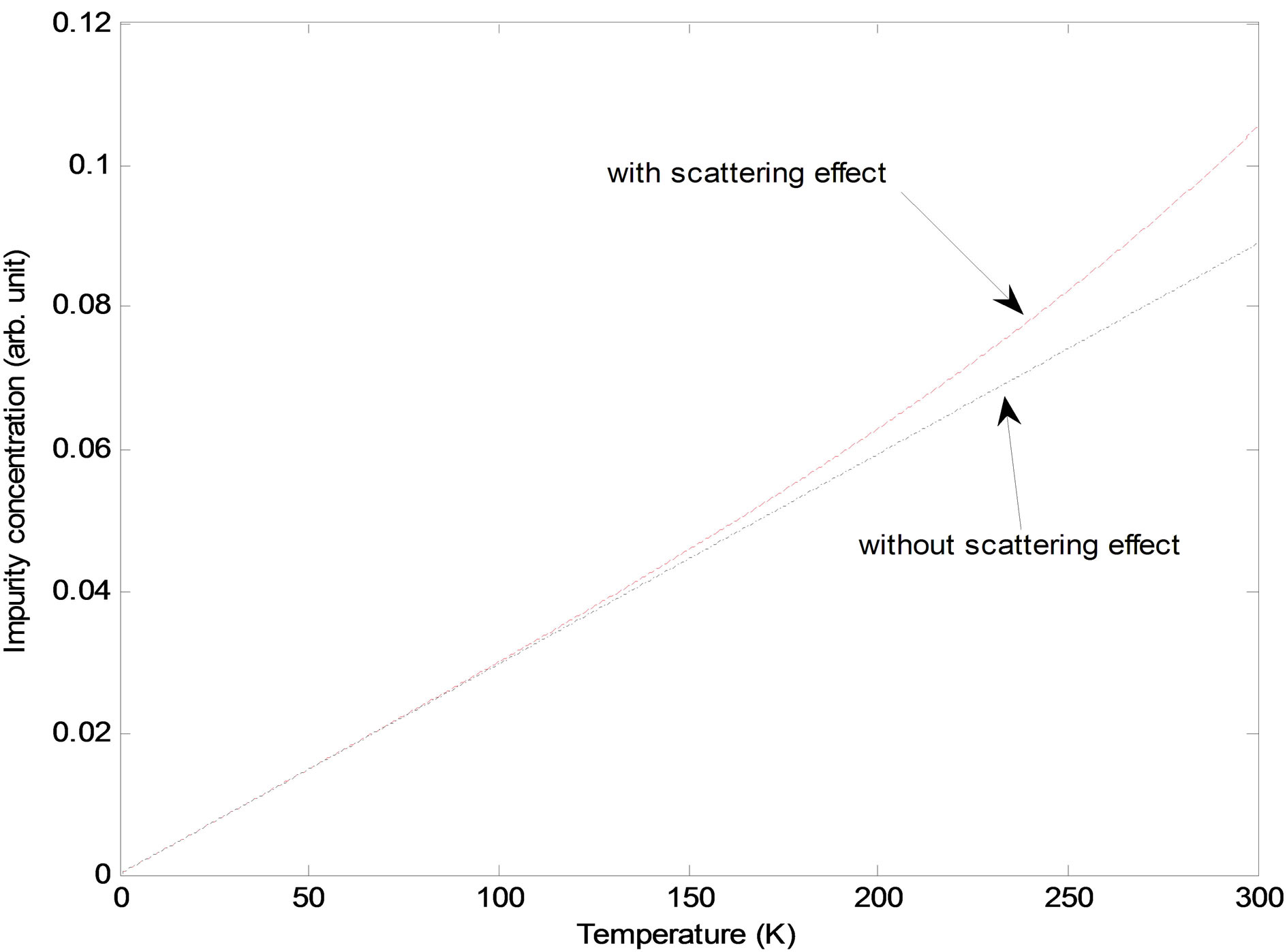
Figure 6. (Colour online) Ferromagnetic transition temperature TC vs. magnetic impurity concentration x for the QW in the absence and presence of spin wave scattering.
peratures effect of magnon-photon interaction and at lower temperatures effect of spin wave scattering is insignificant on magnon heat capacity, Cmag of a quantum wire. As a result the heat capacity is known to rise with decrease in temperature due to the feature that might have altered the ferromagnetic transition temperature, TC. However, magnon-photon interaction effect overwhelms the scattering and lowers the specific heat perhaps improving transport properties of the system elevating density of polarized magnetic spins.
4.2. Specific Heat of the Quantum Well
For (Ga,Mn)As quantum wells, the internal energy can be shown to be γT2 where . The specific heat would vary linearly with temperature and also change with concentration of localized magnetic spins. At sufficiently low temperatures and in the absence of spin wave scattering a result corresponding to the specific heat of dominating electronic contributions in metals [27] is obtained, and also shown in Figure 8. Our analysis indicates that application of light does not affect conditions in quantum wells in general.
. The specific heat would vary linearly with temperature and also change with concentration of localized magnetic spins. At sufficiently low temperatures and in the absence of spin wave scattering a result corresponding to the specific heat of dominating electronic contributions in metals [27] is obtained, and also shown in Figure 8. Our analysis indicates that application of light does not affect conditions in quantum wells in general.
5. Conclusion
In this paper, effect of photo-excitation and spin wave scattering on ferromagnetism of the (Ga,Mn)As DMS QWR and QW are studied in detail. In the case of QWR, ferromagnetic transition temperature TC is shown to decrease with increase in magnetic impurity concentration x but depends on photon magnon interaction strength at sufficiently low temperatures in which Magnetization 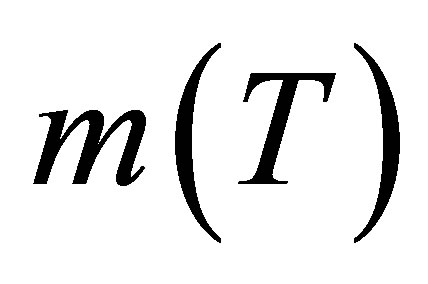 ascends while Cmag curves up decreasing with rise in temperature. Moreover, effect of magnon scattering is insignificant. At higher temperatures, however, ferromagnetic transition temperature, TC increases with rising impurity concentration, x where as magnetization,
ascends while Cmag curves up decreasing with rise in temperature. Moreover, effect of magnon scattering is insignificant. At higher temperatures, however, ferromagnetic transition temperature, TC increases with rising impurity concentration, x where as magnetization, 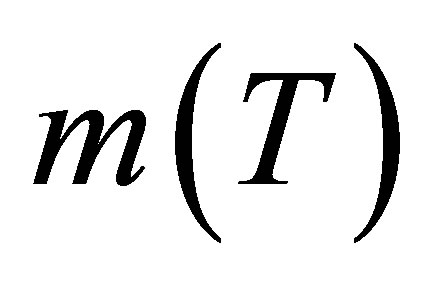 descends. Moreover, the specific heat capacity increases with temperature where inclusion of photon
descends. Moreover, the specific heat capacity increases with temperature where inclusion of photon
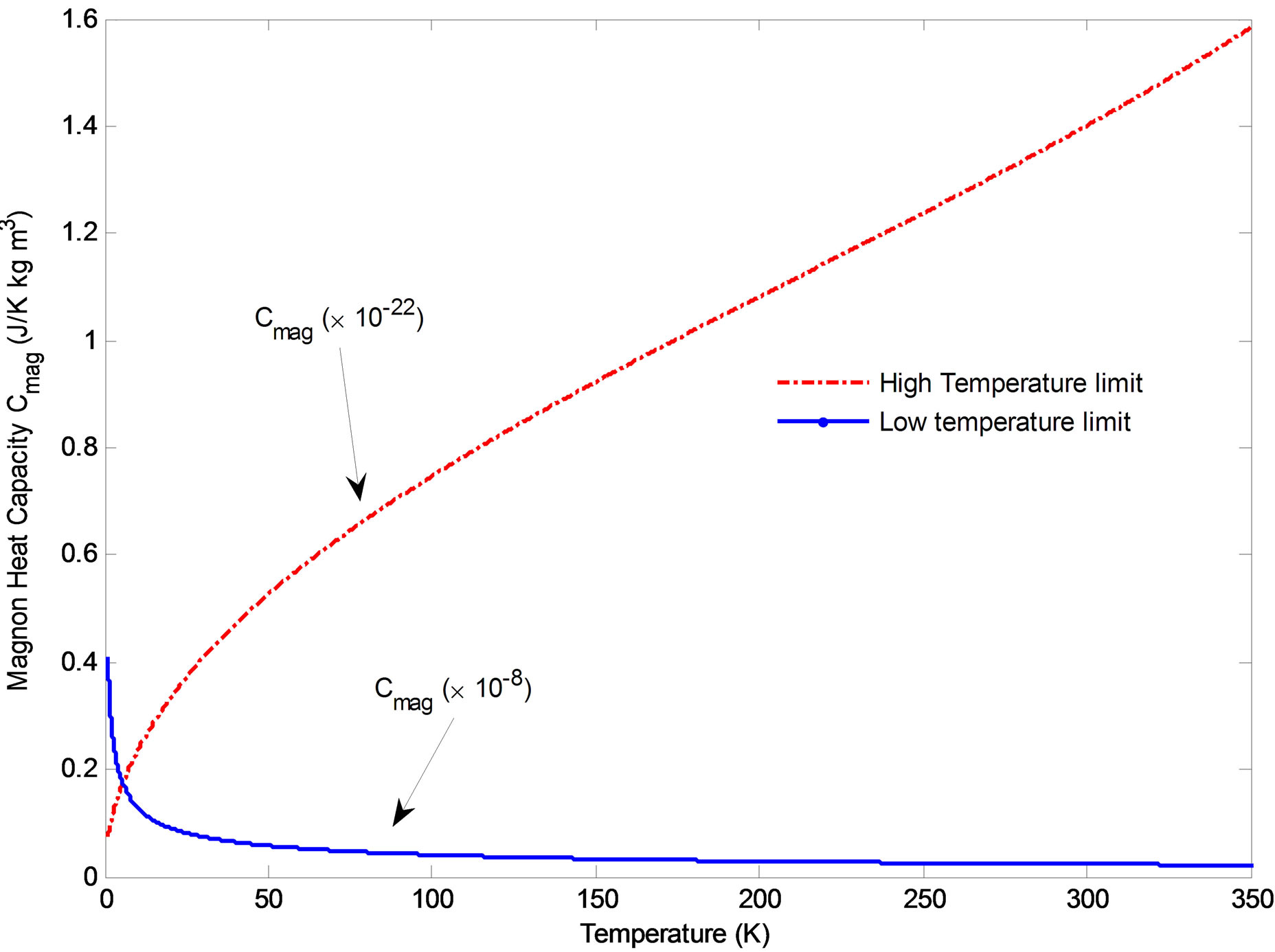
Figure 7. (Colour online) Magnon heat capacity vs. Temperature for a QWR at high and low temperature limits for (Ga,Mn)As. Effect of spin wave scattering is also considered at x = 0.053.

Figure 8. (Colour online) Magnon specific heat Cmag vs. temperature, T for a QW where x = 0.053.
magnon interaction strength is insignificant. In the case of QW, magnetization, 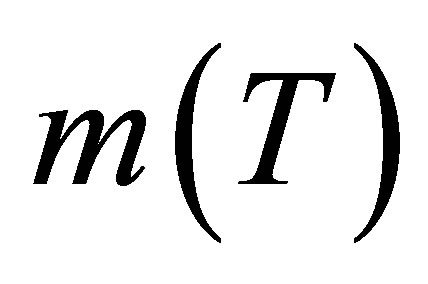 is known to depend on magnon scattering situations and not on light-matter interaction strength generally, and so is for ferromagnetic transition temperature, TC and magnon specific heat, Cmag. Finally, spin wave scattering is known to play an influential role in magnetism of both systems while application of light is insignificant in quantum wells. In both cases the indicated parameters are well understood and affected by doped impurity concentration, and strength of exchange energy, Jnm as in bulk system [15,28].
is known to depend on magnon scattering situations and not on light-matter interaction strength generally, and so is for ferromagnetic transition temperature, TC and magnon specific heat, Cmag. Finally, spin wave scattering is known to play an influential role in magnetism of both systems while application of light is insignificant in quantum wells. In both cases the indicated parameters are well understood and affected by doped impurity concentration, and strength of exchange energy, Jnm as in bulk system [15,28].
6. Acknowledgements
We would like to thank Professor P. Singh, Department of Physics Addis Ababa University, for fruitful discussions. We also acknowledge the financial support from the C. V. Raman fellowship “for African researchers”.
REFERENCES
- M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen van Dau, and F. Pettroff, Physical Review Letters, Vol. 61, 1988, pp. 2472-2475. http://dx.doi.org/10.1103/PhysRevLett.61.2472
- G. Binasch, P. Grunberg, F. Saurenbach and W. Zinn, Physical Review B, Vol. 39, 1989, pp. 4828-4830. http://dx.doi.org/10.1103/PhysRevB.39.4828
- D. A. Neamen, “Semiconductor Physics and Devices: Basic Principles,” Richard D. Irwin, Inc., University of New Mexico, 1992.
- T. Jungwirth, J. Sinova, J. Kučera and A. H. MacDonald, Current Applied Physics, Vol. 3, 2003, pp. 461-464. http://dx.doi.org/10.1016/j.cap.2002.11.001
- T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Science, Vol. 287, 2000, pp. 1019-1022.
- S. Koshihara, A. Oiwa, M. Hirasawa, S. Katsumoto, Y. Iye, C. Urano, H. Takagi and H. Munekata, Physical Review Letters, Vol. 78, 1997, pp. 4617-4620. http://dx.doi.org/10.1103/PhysRevLett.78.4617
- A. Oiwa, Y. Mitsumori, R. Moriya, T. Slupinski and H. Munekata, Physical Review Letters, Vol. 88, 2002, Article ID: 137202. http://dx.doi.org/10.1103/PhysRevLett.88.137202
- H. Munekata, “Inuence of Light on Ferromagnetic Semiconductors: Magnetization Rotation via the Angular Momentum and the Photon Energy,” In: J. Menѐndez and G. Van de Walle, Eds., Proceedings of the 27th International Conference on the Physics of Semiconductors, Melville, Vol. 772, 2005, p. 307.
- E. H. Hwang, A. J. Millis, and S. Das Sarma, Physical Review B, Vol. 65, 2002, pp. 233206-233209. http://dx.doi.org/10.1103/PhysRevB.65.233206
- S. R. Eric Yang, J. Sinova, T. Jungwirth, Y. P. Shim and A. H. MacDonald, Physical Review B, Vol. 67, 2003, pp. 045205-045211. http://dx.doi.org/10.1103/PhysRevB.67.045205
- T. Jungwith, J. Sinova, J. Mašek, J. Kučera and A. H. MacDonald, Reviews of Modern Physics, Vol. 78, 2006, pp. 809-864. http://dx.doi.org/10.1103/RevModPhys.78.809
- A. Rudolph, M. Soda, M. Kiessling, T. Wojtowicz, D. Schuh, W. Wegscheider, J. Zweck, C. Back and E. Reiger, Nano Letters, Vol. 9, 2009, pp. 3860-3866. http://dx.doi.org/10.1021/nl9020717
- J. A. Czaban, D. A. Thompson and R. R. LaPierre, Nano Letters, Vol. 9, 2009, pp. 148-154. http://dx.doi.org/10.1021/nl802700u
- K. Chang, J. B. Xia, H. B. Wu, S. L. Feng and F. M. Peeters, Applied Physics Letters, Vol. 80, 2002, pp. 1788- 1790. http://dx.doi.org/10.1063/1.1459491
- C. Amente and P. Singh, Modern Physics Letters B, Vol. 25, 2011, pp. 273-280.
- D. N. Zubarev, Soviet Physics Uspekhi, Vol. 3, 1960, pp. 320-345. http://dx.doi.org/10.1070/PU1960v003n03ABEH003275
- F. Matsukura, H. Ohno, A. Shen and Y. Sugawara, Physical Review B, Vol. 57, 1998, pp. R2037-R2040. http://dx.doi.org/10.1103/PhysRevB.57.R2037
- T. Kasuya, Progress of Theoretical Physics, Vol. 16, 1956, pp. 45-47. http://dx.doi.org/10.1143/PTP.16.45
- G. Bouzerar, EPL, Vol. 79, 2007, pp. 57007-57011. http://dx.doi.org/10.1209/0295-5075/79/57007
- C. Kittel, “Quantum Theory of Solids,” 2nd Edition, John Wiley and Sons, Inc., University of California, 1987.
- A. Auerbach, “Interacting Electrons and Quantum Magnetism,” Springer, New York, 1994. http://dx.doi.org/10.1007/978-1-4612-0869-3
- H. C. Jeon, T. W. Kang, T. W. Kim, Y. J. Yu, W. Jhe and S. A. Song, Journal of Applied Physics, Vol. 101, 2007, Article ID: 023508.
- R. Dingle, W. Wiegmann and C. H. Henry, Physical Review Letters, Vol. 33, 1974, pp. 827-830. http://dx.doi.org/10.1103/PhysRevLett.33.827
- S. Das Sarma, E. H. Huwang and A. Kaminiski, Physical Review B, Vol. 67, 2003, Article ID: 155201.
- J. Sadowskl, Acta Physica Polonica A, Vol. 114, 2008, pp. 1001-1012.
- S. T. Jang, K. H. Yoo and L. R. Ram-Mohan, Journal of the Korean Physical Society, Vol. 50, 2007, pp. 834-838. http://dx.doi.org/10.3938/jkps.50.834
- C. Kittel, “Introduction to Solid State Physics,” 8th Edition, John Wiley and sons, New York, 2005.
- C. Amente and P. Singh, International Journal of Physical Sciences, Vol. 5, 2010, pp. 671-674.

