Journal of Modern Physics
Vol.4 No.10A(2013), Article ID:38194,7 pages DOI:10.4236/jmp.2013.410A1002
Ionization Process of Atoms by Intense Femtosecond Chirped Laser Pulses
Laboratoire de Physique Computationnelle et Photonique, Université de Moncton Campus de Shippagan, Shippagan, Canada
Email: *stephane.laulan@umoncton.ca
Copyright © 2013 Stéphane Laulan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 25, 2013; revised August 27, 2013; accepted September 26, 2013
Keywords: Hydrogen Atom; Chirped Laser; Multiphoton Ionization; Population Transfer; Nonperturbative Approach
ABSTRACT
We numerically investigate the ionization mechanism in a real hydrogen atom under intense fem to second chirped laser pulses. The central carrier frequency of the pulses is chosen to be 6.2 eV (λ = 200 nm), which corresponds to the fourth-harmonic of the Ti:Sapphire laser. Our simulation of the laser-atom interaction consists on numerically solving the three-dimensional time-dependent Schrödinger equation with a spectral method. The unperturbed wave functions and electronic energies of the atomic system were found by using an L2 discretization technique based on the expansion of the wave functions on B-spline functions. The presented results of kinetic energy spectra of the emitted electrons show the sensitivity of the ionization process to the chirp parameter. Particular attention is paid to the important role of the excited bound states involved in the ionization paths.
1. Introduction
The continuous progress in intense and short laser pulses generation techniques has led to extensive experimental and theoretical investigations on how to use these pulses as tools to control the ultra fast electron dynamic in atomic and molecular systems [1-3]. Recently, physicists took an interest in using chirped laser pulses to investigate laser-matter interactions. These pulses are efficient to control the ionization and excitation mechanisms when compared with unchirped laser pulses, i.e. transformlimited laser pulses [4-9]. The ability to control population transfer from an initial state to a desired final state is of crucial importance as it will open the way to the control of the product yields in chemical reactions.
The most known nonlinear processes that arise in ultra fast laser-matter interactions will change when intense and short chirped laser pulses are used instead of the transform-limited laser pulses [10-14]. The above-threshold ionization (ATI) process is the most important and well-understood nonlinear process by physicists. It is the signature that atoms or molecules can absorb more photons than is strictly necessary for the ionization to occur. The shape of the ATI spectrum, i.e., the kinetic energy spectrum of the emitted electrons, exhibits a series of peaks equally separated by the absorbed incident photon frequency [15-18].
In this paper, we point out the effect of the laser chirp parameter on the kinetic energy spectra of the emitted electrons from the hydrogen atom. We used intense femtosecond chirped laser pulses of central carrier frequency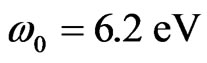 , which corresponded to the fourth-harmonic of the Ti:Sapphire laser. A chirped laser pulse is experimentally produced by chirp filtering of a transform-limited laser pulse. We consider, in this paper, a realistic experimental representation of a linearly polarized chirped laser pulse, in which the chirp parameter increases the time duration of the original transform-limited laser pulse and decreases its intensity. The frequency bandwidth of the resulting chirped pulse remains the same as that of the corresponding transform-limited laser pulse. The theoretical approach we used to calculate the unperturbed energetic structure of the hydrogen atom is based on an
, which corresponded to the fourth-harmonic of the Ti:Sapphire laser. A chirped laser pulse is experimentally produced by chirp filtering of a transform-limited laser pulse. We consider, in this paper, a realistic experimental representation of a linearly polarized chirped laser pulse, in which the chirp parameter increases the time duration of the original transform-limited laser pulse and decreases its intensity. The frequency bandwidth of the resulting chirped pulse remains the same as that of the corresponding transform-limited laser pulse. The theoretical approach we used to calculate the unperturbed energetic structure of the hydrogen atom is based on an 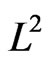 discretization technique using B-spline functions [19,20]. The kinetic energy spectra of the emitted electrons were generated by numerically solving the threedimensional time-dependent Schrödinger equation using a spectral method [21-23]. We follow in time the transfer of the population to the intermediate bound states involved in the ionization paths. We examine then the sensitivity of the excitation mechanism to the sign of the chirp parameter and how that affects the kinetic energy spectra of the emitted electrons.
discretization technique using B-spline functions [19,20]. The kinetic energy spectra of the emitted electrons were generated by numerically solving the threedimensional time-dependent Schrödinger equation using a spectral method [21-23]. We follow in time the transfer of the population to the intermediate bound states involved in the ionization paths. We examine then the sensitivity of the excitation mechanism to the sign of the chirp parameter and how that affects the kinetic energy spectra of the emitted electrons.
Atomic units (a.u.) are used throughout the paper unless otherwise mentioned.
2. Theoretical Approach
2.1. Atomic Structure Calculations
The time-independent Schrödinger equation (TISE) describing the electron motion around the atomic nucleus is given by:
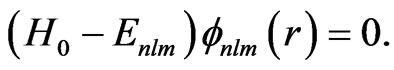 (1)
(1)
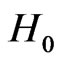 is the nonrelativistic field-free Hamiltonian in spherical coordinates, which reads
is the nonrelativistic field-free Hamiltonian in spherical coordinates, which reads
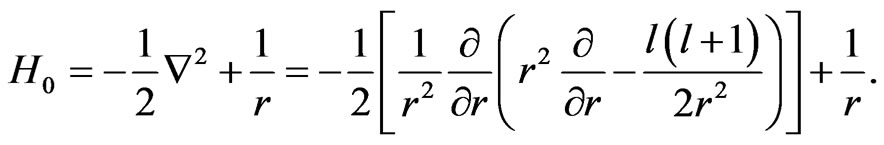 (2)
(2)
For a given electron angular momentum l and projection m, the solution of Equation (1) can be written as follows:
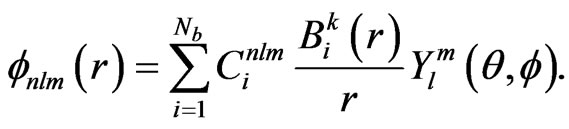 (3)
(3)
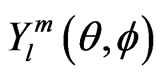 is the spherical harmonic functions depending on angular coordinates. The B-spline function of order k denoted by
is the spherical harmonic functions depending on angular coordinates. The B-spline function of order k denoted by 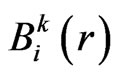 is a piecewise polynomial of degree k-1 [20]. We use
is a piecewise polynomial of degree k-1 [20]. We use 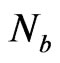 B-spline functions, that are distributed along the radial axis, in a radial box defined from
B-spline functions, that are distributed along the radial axis, in a radial box defined from 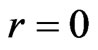 to
to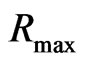 . A direct diagonalization of Equation (1) gives the unperturbed eigenenergies
. A direct diagonalization of Equation (1) gives the unperturbed eigenenergies 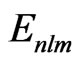 and eigenfunctions of all bound and continuum discretized states. We have proven the efficiency of our discretization technique in previous works on two-active electron systems [21-23].
and eigenfunctions of all bound and continuum discretized states. We have proven the efficiency of our discretization technique in previous works on two-active electron systems [21-23].
2.2. Time-Dependent Calculations
Within the electric dipole approximation, the time-dependent Schrödinger equation (TDSE) describing the electron motion in the presence of the laser field is given by:
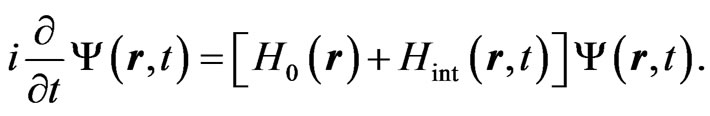 (4)
(4)
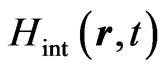 describes the interaction of the electron with the laser field. It could be expressed in different gauges as for example the length or velocity gauges. As we adopt here the velocity gauge,
describes the interaction of the electron with the laser field. It could be expressed in different gauges as for example the length or velocity gauges. As we adopt here the velocity gauge,  is written as the scalar product of the potential vector and the electron momentum:
is written as the scalar product of the potential vector and the electron momentum:
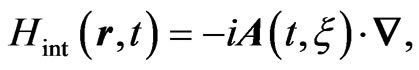 (5)
(5)
where 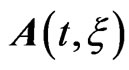 is the vector potential of the chirped laser pulse linearly polarized along the z axis. The timedependent total wave function
is the vector potential of the chirped laser pulse linearly polarized along the z axis. The timedependent total wave function 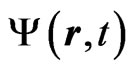 in Equation (4) is expanded on the basis of the field-free atomic eigenstates, normalized to unity,
in Equation (4) is expanded on the basis of the field-free atomic eigenstates, normalized to unity,
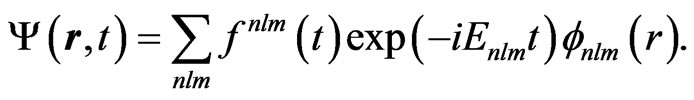 (6)
(6)
By substituting Equation (6) into Equation (4), we obtain a set of coupled integro-differential equations, which we solved using an explicit fifth-order Runge-Kutta numerical method [21].
The vector potential of the chirped laser pulse considered here is given by:
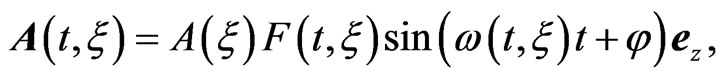 (7)
(7)
With ξ is the chirp parameter, 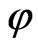 the pulse carrierenvelope phase (CEP),
the pulse carrierenvelope phase (CEP), 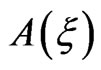 the peak amplitude,
the peak amplitude, 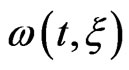 the instantaneous frequency and
the instantaneous frequency and 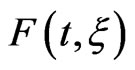 the Gaussian time envelope. We note that, in experiment, chirp filters are implemented by use of dispersive optical systems. Upon transmission through a filter characterized by a b chirp coefficient, an initially transform-limited pulse
the Gaussian time envelope. We note that, in experiment, chirp filters are implemented by use of dispersive optical systems. Upon transmission through a filter characterized by a b chirp coefficient, an initially transform-limited pulse 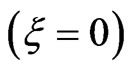 becomes chirped, i.e., with frequency
becomes chirped, i.e., with frequency 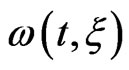 that varies in time and depends on the chirp parameter
that varies in time and depends on the chirp parameter 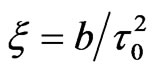 (for the experimental details see [24]).
(for the experimental details see [24]). 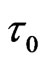 is the full width at half maximum (FWHM) duration of the transform-limited pulse. The filtered pulse will be up-chirped if
is the full width at half maximum (FWHM) duration of the transform-limited pulse. The filtered pulse will be up-chirped if 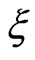 is positive and will be downchirped if
is positive and will be downchirped if 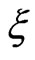 is negative.
is negative.
The expression of 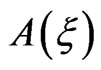 is given by :
is given by :
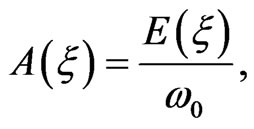 (8)
(8)
where 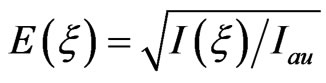 is the electric field amplitude of the chirped pulse, with
is the electric field amplitude of the chirped pulse, with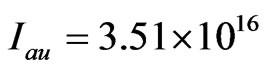 W·cm−2the atomic unit of intensity and
W·cm−2the atomic unit of intensity and 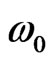 the central carrier frequency. The intensity of the chirped pulse
the central carrier frequency. The intensity of the chirped pulse 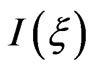 is related to the intensity
is related to the intensity 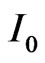 of the transform-limited pulse
of the transform-limited pulse 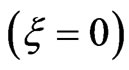 by:
by:
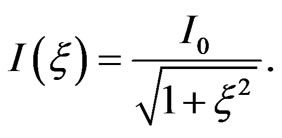 (9)
(9)
The instantaneous frequency 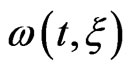 and the Gaussiantime envelope
and the Gaussiantime envelope 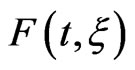 are given, respectively, by :
are given, respectively, by :
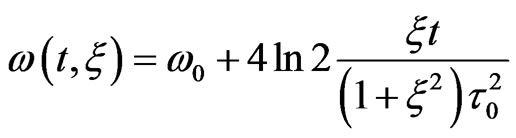 (10)
(10)
and
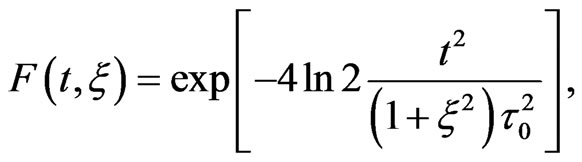 (11)
(11)
The FWHM duration of the chirped pulse is given by:
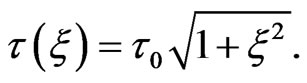 (12)
(12)
At the switch-off of the laser pulse , the probability of finding the systemin the
, the probability of finding the systemin the 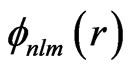 electronic eigenstate is given by:
electronic eigenstate is given by:
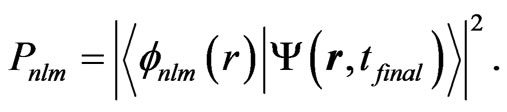 (13)
(13)
The kinetic energy spectrum of the emitted electrons is calculated as follows:
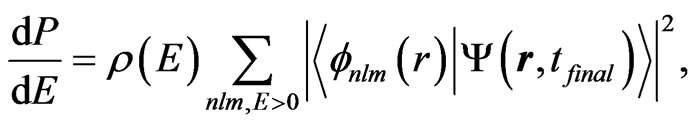 (14)
(14)
with 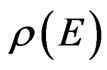 the density of continuum states [20].
the density of continuum states [20].
3. Results and Discussions
For the numerical calculations, we have considered a set of 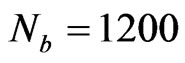 B-splines of order
B-splines of order 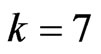 defined on the radial box of maximum length
defined on the radial box of maximum length 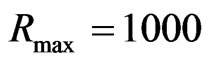 a.u.. We have fixed the maximum electron angular momentum to
a.u.. We have fixed the maximum electron angular momentum to . As we choose the laser pulse to be polarized linearly along the z axis, only electronic transitions between states of
. As we choose the laser pulse to be polarized linearly along the z axis, only electronic transitions between states of 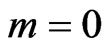 magnetic quantum number are permitted. We kept in all our calculations the CEP constant and set to
magnetic quantum number are permitted. We kept in all our calculations the CEP constant and set to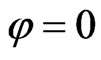 . The convergence of our numerical results has been checked by increasing the number of B-sp line functions, the radial box size and the number of angular moment a. We have also checked that the results are gauge independent.
. The convergence of our numerical results has been checked by increasing the number of B-sp line functions, the radial box size and the number of angular moment a. We have also checked that the results are gauge independent.
We consider in this paper a transform-limited pulse (ξ = 0) of central carrier frequency ω0 = 0.228 a.u. (6.2 eV), which corresponds to the fourth-harmonic of Ti:Sa laser (λ = 200 nm). The pulse has an intensity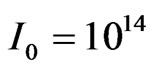 W·cm−2 and a FWHM duration τ0 = 137.79 a.u. =3.33 fs.
W·cm−2 and a FWHM duration τ0 = 137.79 a.u. =3.33 fs.
We plot in Figure 1 the transform-limited pulse vector potential  variation with time. We compare in the same figure
variation with time. We compare in the same figure 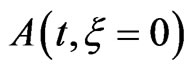 with the vector potentials of a simulated filtered up-chirped pulse of
with the vector potentials of a simulated filtered up-chirped pulse of 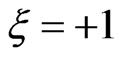 and a down-chirped pulse of
and a down-chirped pulse of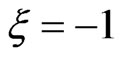 . Both chirped pulses, according to Equations (9) and (12), have an intensity of
. Both chirped pulses, according to Equations (9) and (12), have an intensity of 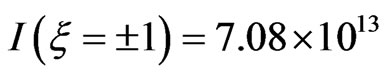 W∙cm−2 and a FWHM duration
W∙cm−2 and a FWHM duration 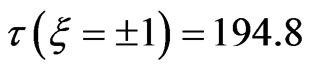 a.u. = 4.7 fs. The form of the vector potential used in this paper (see Equation (7)) simulates a realistic experimental case in which the chirp filtering decreases the intensity of the transform-limited pulse and increases its total duration. We also present in Figure 1 the spectral profile of the three pulses and the variation of their instantaneous frequency ω(t, ξ) with time. Specifically, an up-chirped pulse (down-chirped) with a positive (negative) value of ξ means that the instantaneous laser frequency increases (decreases) with time. Nevertheless, the frequency bandwidth of the upand down-chirped pulses remains the same as that of the transform-limited pulse.
a.u. = 4.7 fs. The form of the vector potential used in this paper (see Equation (7)) simulates a realistic experimental case in which the chirp filtering decreases the intensity of the transform-limited pulse and increases its total duration. We also present in Figure 1 the spectral profile of the three pulses and the variation of their instantaneous frequency ω(t, ξ) with time. Specifically, an up-chirped pulse (down-chirped) with a positive (negative) value of ξ means that the instantaneous laser frequency increases (decreases) with time. Nevertheless, the frequency bandwidth of the upand down-chirped pulses remains the same as that of the transform-limited pulse.
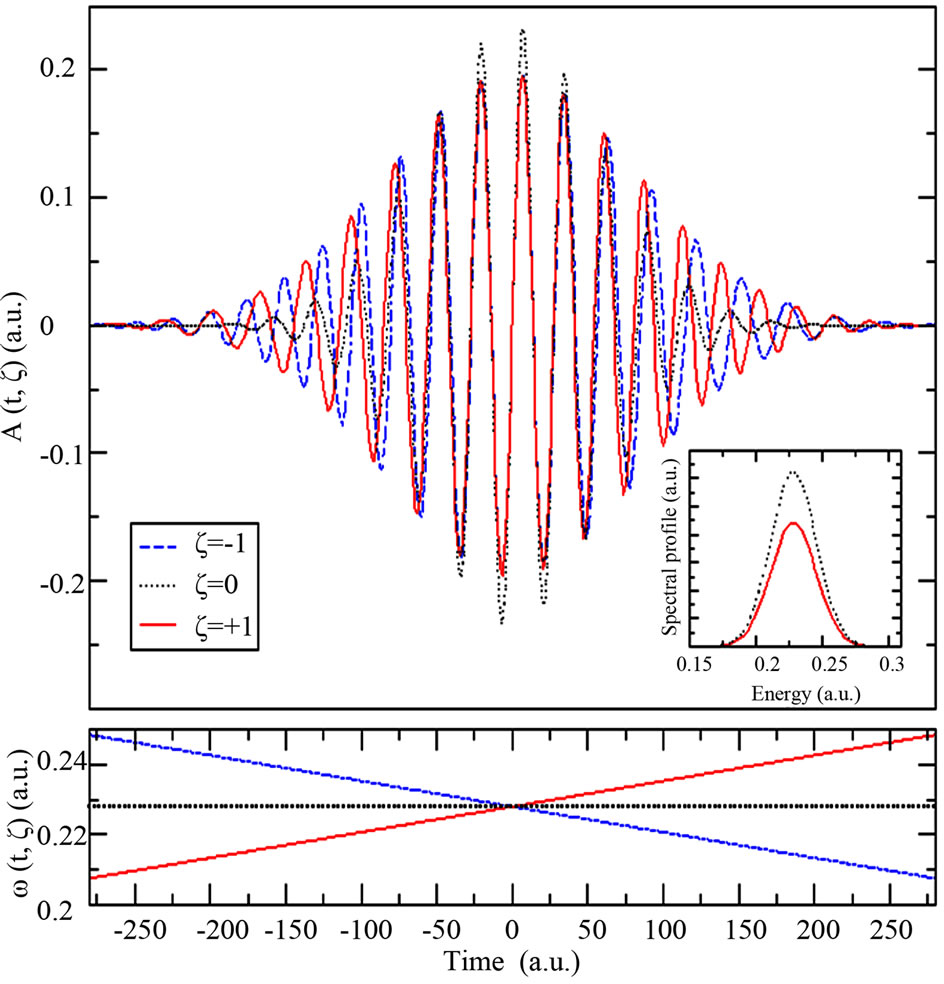
Figure 1. Dependence of laser pulse vector potential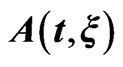 , spectral profile and instantaneous frequency
, spectral profile and instantaneous frequency 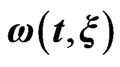 on the chirp parameter
on the chirp parameter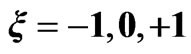 . The chirped pulses
. The chirped pulses 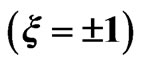 have a central carrier frequency
have a central carrier frequency 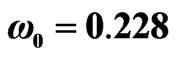 a.u. (6.2 eV), CEP
a.u. (6.2 eV), CEP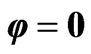 , intensity
, intensity 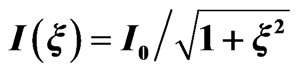 and FWHM duration
and FWHM duration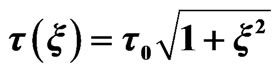 , where
, where  W∙cm−2 and
W∙cm−2 and 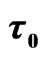 are respectively the intensity and the FWHM duration of the transform-limited pulse
are respectively the intensity and the FWHM duration of the transform-limited pulse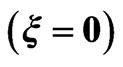 .
.
We submit the hydrogen atom to each of three pulses showed in Figure 1. In Figure 2, we compare in logarithmic scale the kinetic energy spectra of the emitted electrons we obtained at the end of each pulse interaction with the atom. The spectra exhibit a number of peaks that are the signature of the ATI nonlinear process by which the atom, under these intense laser pulses, has absorbed S more photons than the minimum number of three photons necessary to reach the ionization limit (IP = 0.5 a.u. = 13.6 eV). The many peaks observed in kinetic energy spectra of the emitted electrons have relatively narrow widths, and are centered on electronic energies ES given by:
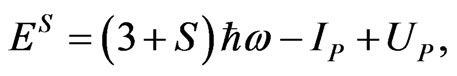 (15)
(15)
where 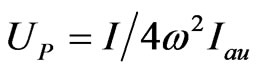 is the electron ponderomotive energy. The hydrogen atom under a strong pulse of intensity I and photon frequency ω experiences an ionization potential increase of UP.
is the electron ponderomotive energy. The hydrogen atom under a strong pulse of intensity I and photon frequency ω experiences an ionization potential increase of UP.
We notice in Figure 2 that a nonzero chirp value affects the height and position of the peaks. The down-chirped pulse (up-chirped pulse) moves slightly the ATI peaks to the left (right) when compared to the unchirped pulse. The modification in the ATI shape and properties is a result of
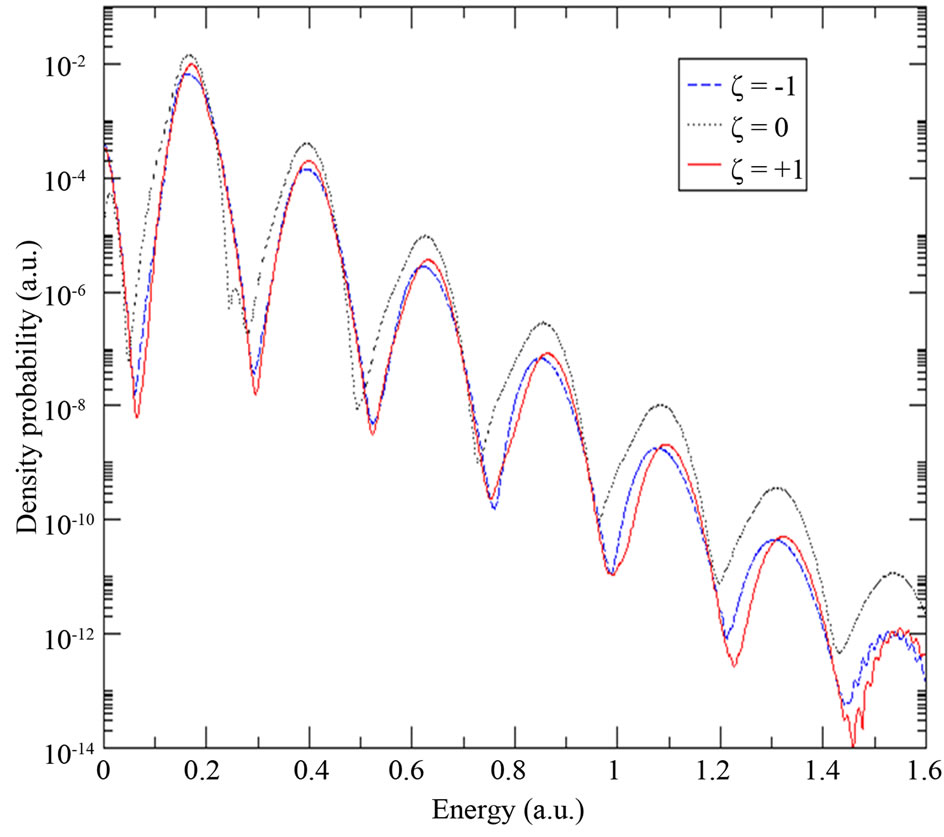
Figure 2. Kinetic energy spectra of the emitted electrons obtained at the end of chirped pulses with 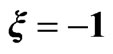 (dashed line),
(dashed line), 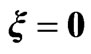 (dotted line) and
(dotted line) and 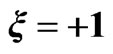 (solid line) in logarithmic scale (1 a.u. of energy is equivalent to 27.2 eV).
(solid line) in logarithmic scale (1 a.u. of energy is equivalent to 27.2 eV).
how the sign of the chirp influences the time variation of the instantaneous frequency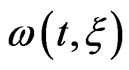 , which affects the energy shift of the excited states and then the energy of emitted electrons.
, which affects the energy shift of the excited states and then the energy of emitted electrons.
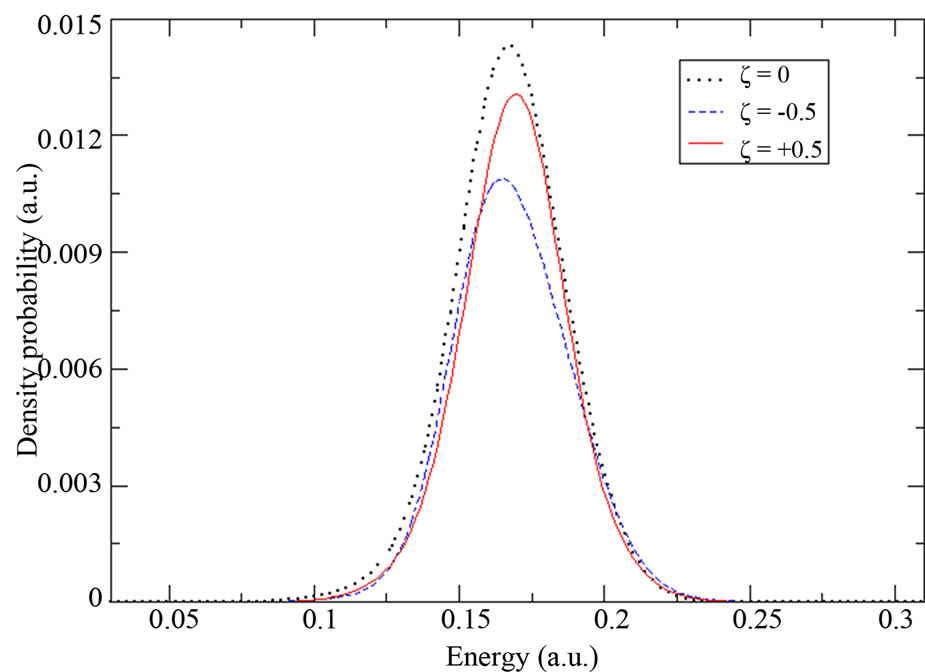
Let us now observe more precisely if the sensitivity of the ionization process will persist for other chirp parameter values. In Figures 3(a)-(d), we present in nonlogarithmic scale the first peak 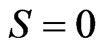 of the emitted electron energy spectrum which is due to the ionization of the atom with three photons. The results were obtained at the end of the laser pulses with the following chirp parameters
of the emitted electron energy spectrum which is due to the ionization of the atom with three photons. The results were obtained at the end of the laser pulses with the following chirp parameters 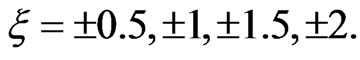 We compare in each case the chirped pulses
We compare in each case the chirped pulses 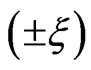 results with that obtained with the unchirped pulse
results with that obtained with the unchirped pulse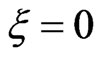 . In the first case
. In the first case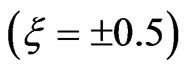 , the intensity of the upand down-chirped pulses is
, the intensity of the upand down-chirped pulses is 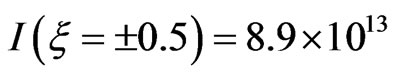 W∙cm−2 and their FWHM duration is
W∙cm−2 and their FWHM duration is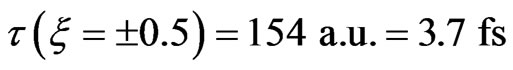 . In the second case
. In the second case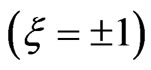 , the intensity and the FWHM duration of the chirped pulses are the same used previously. In the third case,
, the intensity and the FWHM duration of the chirped pulses are the same used previously. In the third case, 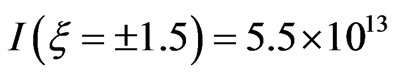 W∙cm−2 and
W∙cm−2 and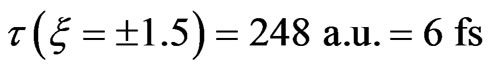 . Finally, in the fourth case,
. Finally, in the fourth case,
 (a)
(a)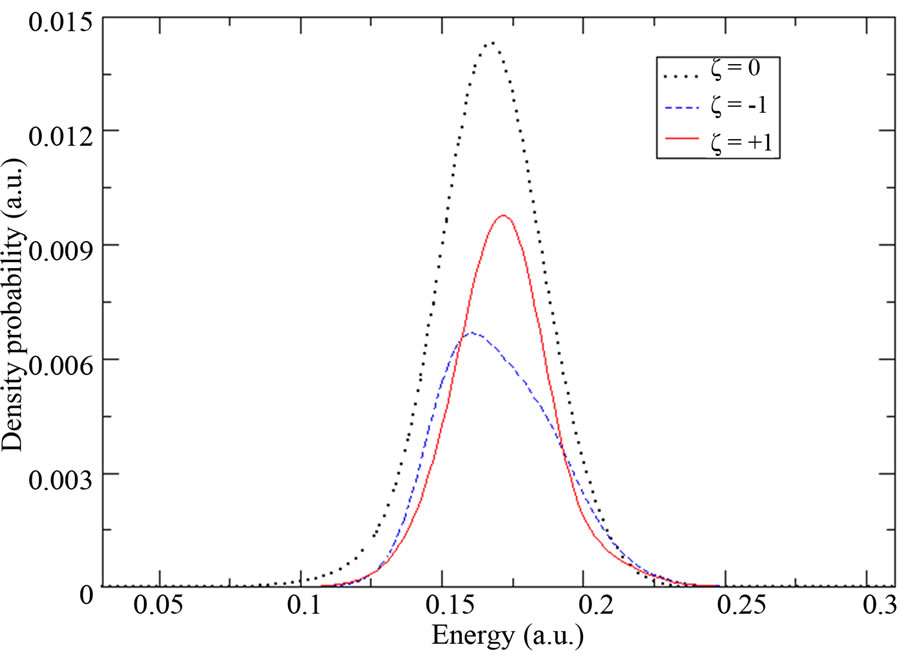 (b)
(b)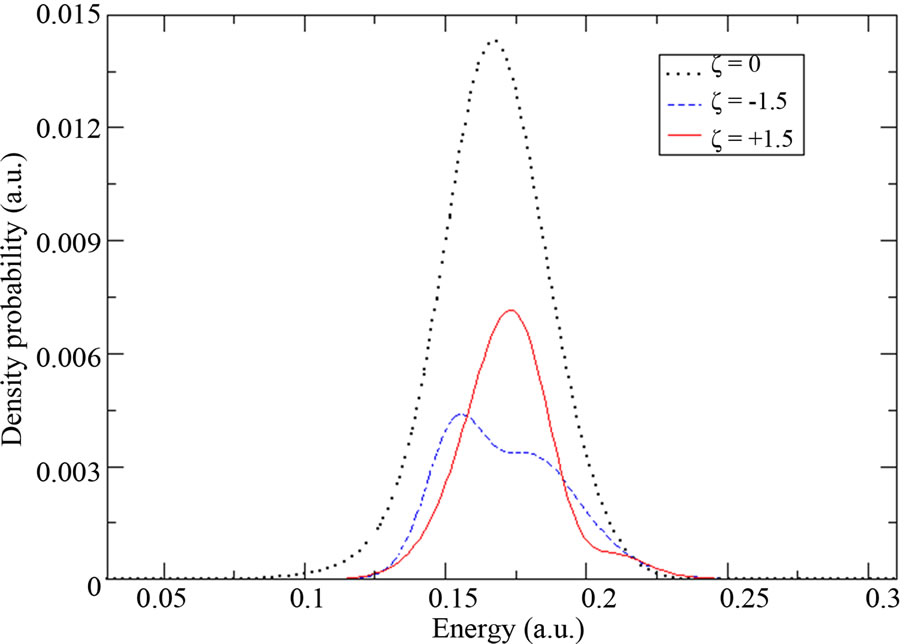 (c)
(c)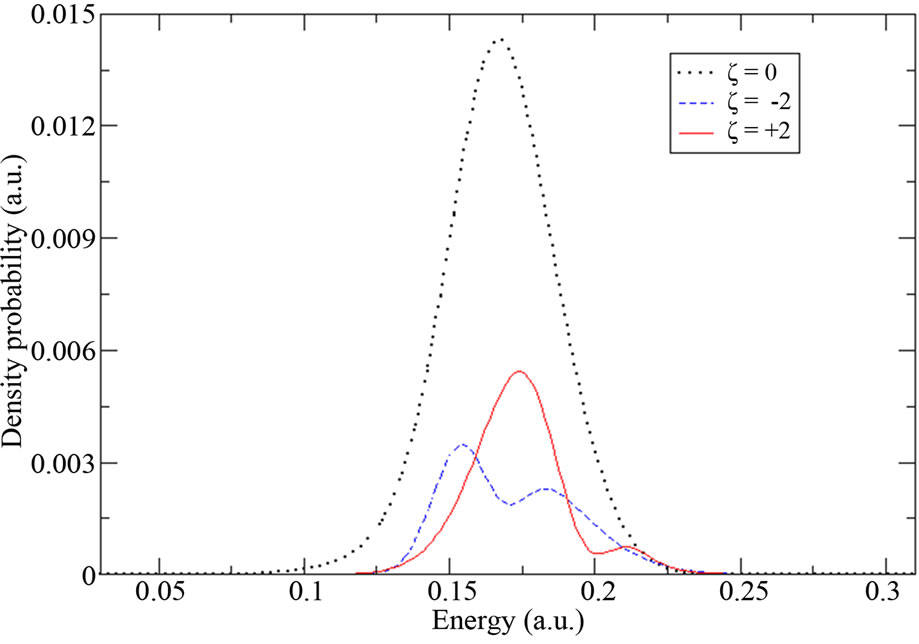 (d)
(d)
Figure 3. Peaks S = 0 of the emitted electron energy spectrum obtained at the end of laser pulses with (a) ξ = 0, ±0.5; (b) ξ = 0, ±1; (c) ξ = 0, ±1.5 and (d) ξ = 0, ±2 in nonlogarithmic scale. Solid line (dashed line) corresponds to the results obtained with a positive (negative) chirp parameter, and dotted line with ξ = 0.
the intensity decreases to 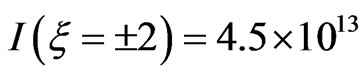 W∙cm−2 and the duration increases to
W∙cm−2 and the duration increases to .
.
When we compare between the results presented in Figure 3, we first notice that in each of the four cases, the emitted electron energy spectrum obtained with the unchirped pulse has higher magnitude than those obtained with the chirped laser pulses, which is expected as the intensity of unchirped pulse is higher than that of chirped pulses. Secondly, the increasing of 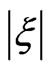 seems to produce only a slight Stark shift of the emitted electron spectrum towards higher electronic energies when the atom is under the up-chirped pulse. In contrast, when the atom is submitted to the down-chirped pulse, we observe a slight energy shift towards lower electronic energies with, however, a visible break-up of the ionization peak into two narrow peaks.
seems to produce only a slight Stark shift of the emitted electron spectrum towards higher electronic energies when the atom is under the up-chirped pulse. In contrast, when the atom is submitted to the down-chirped pulse, we observe a slight energy shift towards lower electronic energies with, however, a visible break-up of the ionization peak into two narrow peaks.
The significant change in the shape of the emitted electron energy spectra, particularly with adown-chirped laser pulse, results from the sensitivity of the excitation process to the sign of the chirp parameter. The latter affects the average of the population transferred to the intermediate bound states involved in the ionization paths. To prove the role of the excited bound states in this study, we removed them all from the atomic basis set and then we solved the TDSE. We have found that the chirp influence on ATI spectra has totally disappeared.
Figure 4 indicates the excitation scheme induced by the laser frequency ω0 = 0.228 a.u.. To understand the influence of the chirp parameter on the excitation mechanism, we have examined how the population of the excited states by the up-chirped laser pulse takes place compared to the down-chirped pulses. We followed in time the population of the 2s, 2p, 3s, 4s, 3d and 4d bound states in the presence of the chirped pulses of 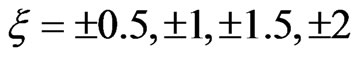 used previously. We found that the 2s and 2p bound electronic states, off-resonance, are not affected by the chirp in contrast with the 3s, 4s, 3d and 4d states that are close to resonance by two-photon transition from the 1s. We also found that the 3d and 4d excited states are much more populated than the 3s and 4s states. The ionization occurs mostly by electrons transition from the
used previously. We found that the 2s and 2p bound electronic states, off-resonance, are not affected by the chirp in contrast with the 3s, 4s, 3d and 4d states that are close to resonance by two-photon transition from the 1s. We also found that the 3d and 4d excited states are much more populated than the 3s and 4s states. The ionization occurs mostly by electrons transition from the 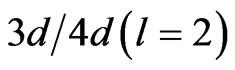 states to the
states to the 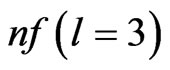 continuum channel and feebly from the
continuum channel and feebly from the 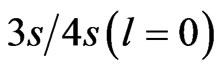 states to the
states to the 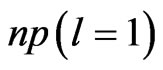 continuum channel.
continuum channel.
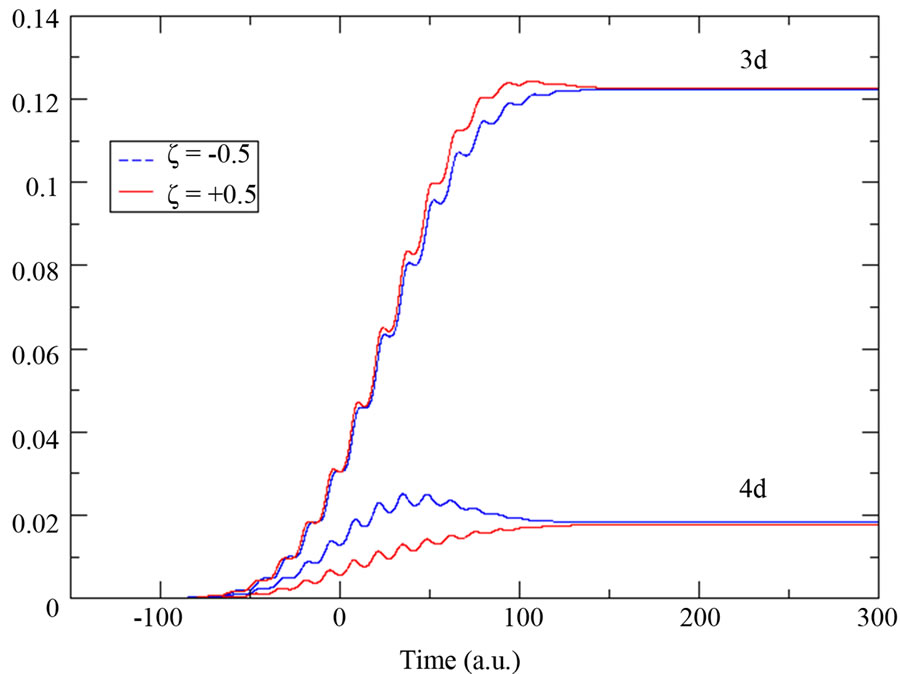
So, we only report in Figure 5 the time evolution of the 3d and 4d bound states population. We notice that the population of the 3d state decreases when we increase the chirp parameter and also that the down-chirp pulse populates the 4d state more than an up-chirped pulse does. During its time duration, an up-chirped pulse induces a two-photon resonant transition from the fundamental state 1s to the 3d first and from 1s to the 4d later in time. In contrast, a down-chirped pulse induces a two-photon
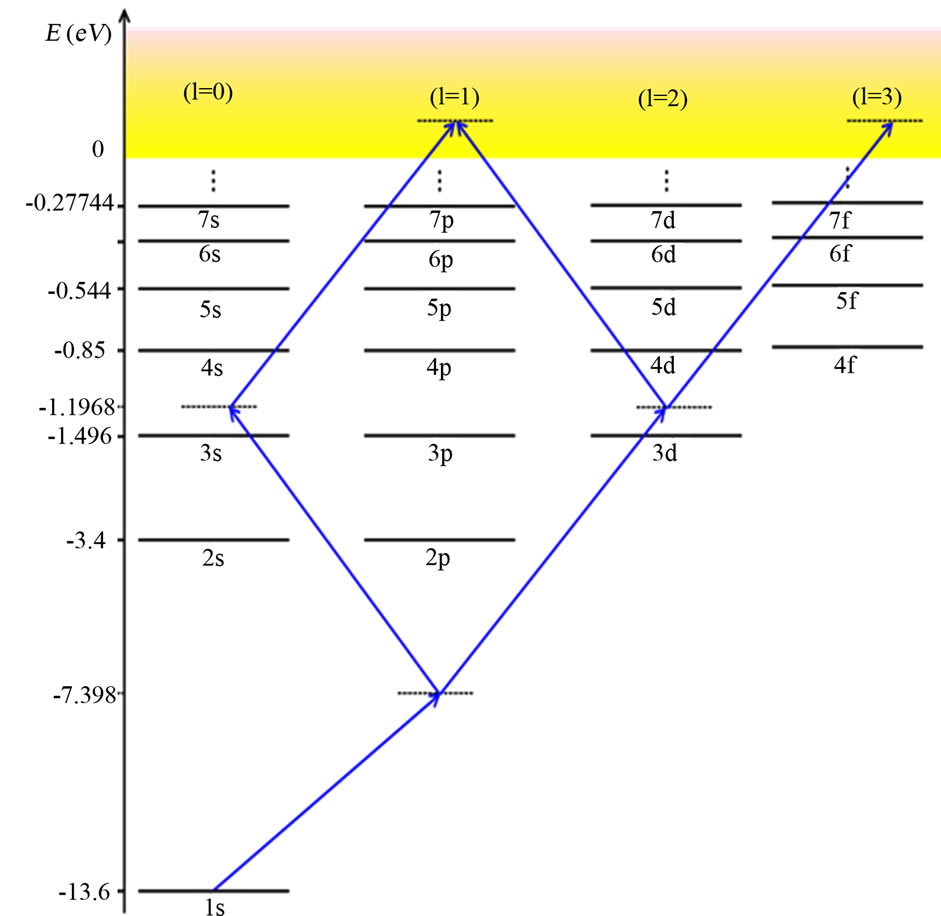
Figure 4. Schematic hydrogen atom energy level diagram showing the ionization paths with a laser pulse of central carrier frequency ω0 = 0.228 a.u..
resonant transition from the 1s to the 4d first and from 1s to the 3d later in time. That explains why in Figure 5 the 4d state is more(less) populated when the atom is under down-chirped (up-chirped) pulse.
The double peaks structure observed in Figures 3(c) and (d), when we fix the value of the chirp parameter to 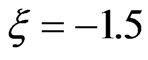 and
and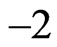 , is essentially due to two factors. The first is by increasing
, is essentially due to two factors. The first is by increasing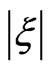 , we decrease the laser intensity, so the population of the 3d state decreases as it becomes then less coupled to 1s by resonant two-photon transition. The second is a chirped pulse with a negative ξ increases the population of the 4d state. Ionization, in this case, occurs by the transfer of the population from both the 3d and 4d states to the
, we decrease the laser intensity, so the population of the 3d state decreases as it becomes then less coupled to 1s by resonant two-photon transition. The second is a chirped pulse with a negative ξ increases the population of the 4d state. Ionization, in this case, occurs by the transfer of the population from both the 3d and 4d states to the  continuum channel causing the appearance of the two narrow peaks observed in the emitted electron energy spectra. In contrast with the case when we decrease (increase) the chirp parameter (laser intensity), see Figures 3(a) and (b), here the transfer of the population occurs predominantly from the most populated 3d state to the continuum. Here, no double narrow peaks structure is observed.
continuum channel causing the appearance of the two narrow peaks observed in the emitted electron energy spectra. In contrast with the case when we decrease (increase) the chirp parameter (laser intensity), see Figures 3(a) and (b), here the transfer of the population occurs predominantly from the most populated 3d state to the continuum. Here, no double narrow peaks structure is observed.
The excitation mechanism could be controlled by chirped laser pulses. By varying the sign of the chirp parameter, the instantaneous frequency changes in time differently, which induces different excitation scenarios. With chirped laser pulses, we could determine which level will have a bigger average population during the laser-atom interaction and thus control the ionization yield. We have investigated the sensitivity of the ionization process to the chirp parameter for various other harmonic frequencies of Ti:Sa laser. We have observed that the sensitivity is generally more accentuated when the chirp
 (a)
(a)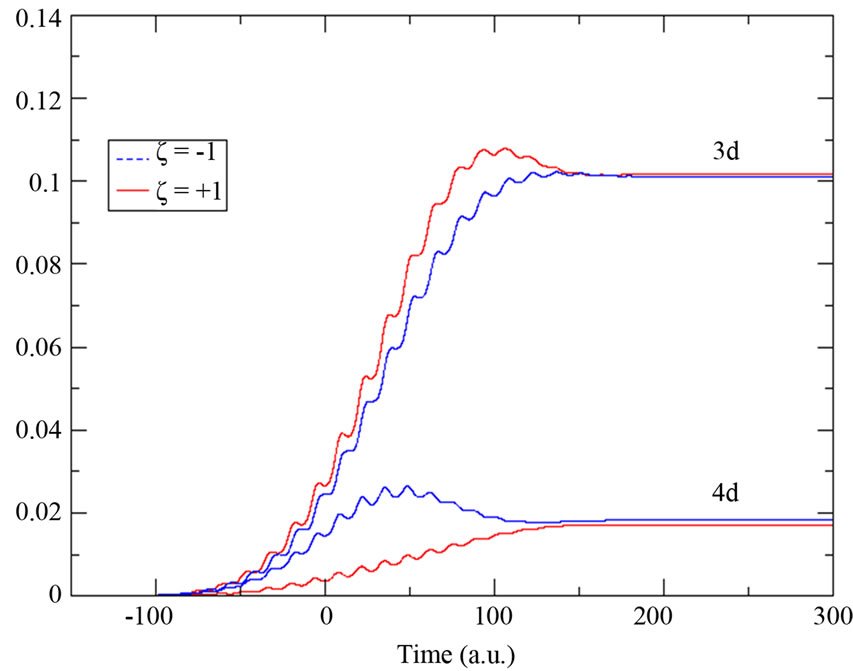 (b)
(b)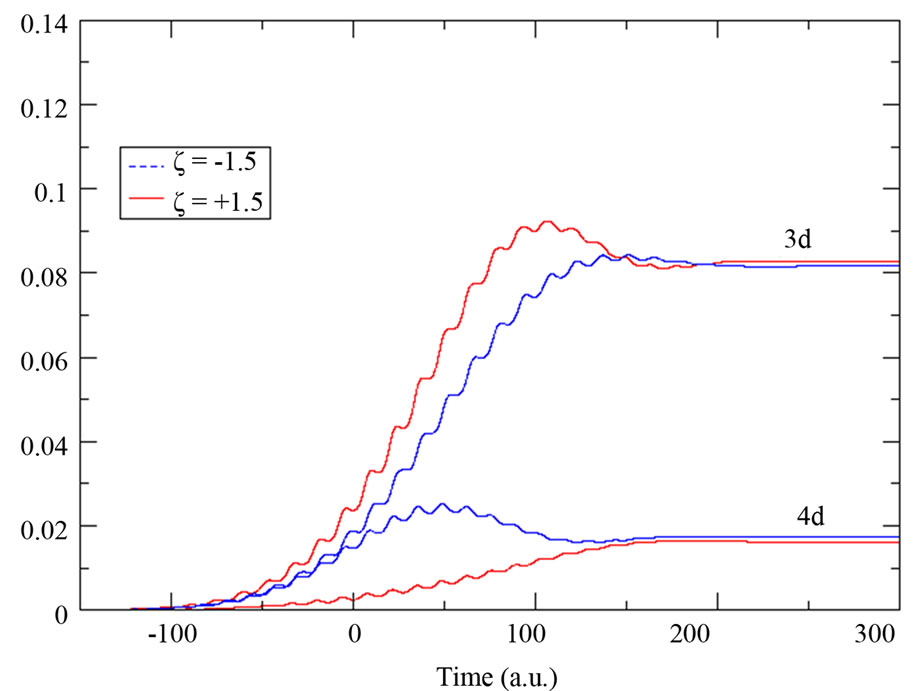 (c)
(c)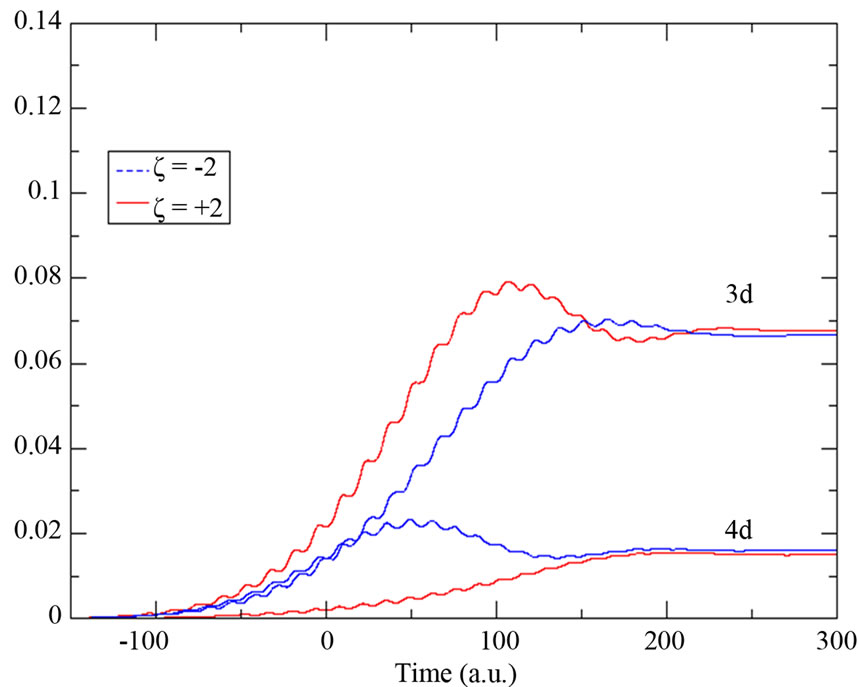 (d)
(d)
Figure 5. Population of the 3d and 4d bound states in the presence of up-chirped (solid line) and down-chirped (dashed line) laser pulses of (a) ξ = ±0.5; (b) ξ = ±1; (c) ξ = ±1.5 and (d) ξ = ±2.
induces resonant transitions in the excitation mechanism.
4. Conclusion
We have presented in this paper the results of numerical calculations of the emitted electron energy spectra in the hydrogen atom under intense fem to second chirped laser pulses. We have observed that the ionization and excitation dynamics are very sensitive to the chirp parameter. Intense ultra short chirped laser pulses could be an important tool to study image and control the electron dynamic in atoms and molecules. The study presented in this paper could be applicable to control the transfer or the inversion of the population in another atomic target. The chirp dependence of the emitted electron energy spectra observed here may prove useful for experimental characterization of chirped laser pulses.
5. Acknowledgements
The present research was supported by the NSERC and by the New Brunswick Innovation Foundation (NBIF). Allocation of CPU time and assistance with the computer facilities from the Atlantic Computational Excellence Network (ACE net, St-John’s, NL, Canada) and from the “Réseau Québecois de Calcul de Haute Performance” are acknowledged.
REFERENCES
- J. C. Diels and W. Rudolph, “Ultrashort Laser Pulse Phenomenon: Fundamentals, Techniques and Applications on Femtosecond Time Scale,” Academic Press, New York, 1996.
- P. Agostini and L. F. DiMauro, Reports on Progress in Physics, Vol. 67, 2004, pp. 813-855. http://dx.doi.org/10.1088/0034-4885/67/6/R01
- K. Yamanouchi, S. L. Chin, P. Agostini and G. Ferrante, “Progress in Ultrafast Intense Laser Science III,” SpringerVerlag, New York, 2007.
- R. B. Vrijen, D. I. Duncan and L. D. Noordam, Physical Review A, Vol. 56, 1997, pp. 2205-2212. http://dx.doi.org/10.1103/PhysRevA.56.2205
- K. J. Schafer and K. C. Kulander, Laser Physics, Vol. 7, 1997, pp. 740-750.
- J. Cao, C. J. Barden and K. R. Wilson, Journal of Chemical Physics, Vol. 113, 2000, pp. 1898-1909. http://dx.doi.org/10.1063/1.481993
- J. Lambert, M. W. Noel and T. F. Gallagher, Physical Review A, Vol. 66, 2002, Article ID: 053413. http://dx.doi.org/10.1103/PhysRevA.66.053413
- C. W. S. Conover, M. C. Doogue and F. J. Struwe, Physical Review A, Vol. 65, 2002, Article ID: 033414. http://dx.doi.org/10.1103/PhysRevA.65.033414
- V. Prasad, B. Dahija and K. Yamashita, PhysicaScripta, Vol. 82, 2010, Article ID: 055302. http://dx.doi.org/10.1088/0031-8949/82/05/055302
- Marani and E. J. Robinson, Journal of Physics B, Vol. 32, 1999, pp. 711-736. http://dx.doi.org/10.1088/0953-4075/32/3/014
- J. Wu, G. T. Zhang, C. L. Xia and X. S. Liu, Physical Review A, Vol. 82, 2010, Article ID: 013411.
- J. J. Carrera and S. I. Chu, Physical Review A, Vol. 75, 2007, Article ID: 033807. http://dx.doi.org/10.1103/PhysRevA.75.033807
- T. Nakajima, Physical Review A, Vol. 75, 2007, Article ID: 053409. http://dx.doi.org/10.1103/PhysRevA.75.053409
- Y. Xiang, Y. Niu and S. Gong, Physical Review A, Vol. 80, 2009, Article ID: 023423. http://dx.doi.org/10.1103/PhysRevA.80.023423
- P. Agostini, F. Fabre, G. Mainfray, G. Petite and N. K. Rahman, Physical Review Letters, Vol. 42, 1979, pp. 1127- 1130. http://dx.doi.org/10.1103/PhysRevLett.42.1127
- J. Javanainen, J. H. Eberly and Q. Su, Physical Review A, Vol. 38, 1988, pp. 3430-3446. http://dx.doi.org/10.1103/PhysRevA.38.3430
- W. Becker, F. Grasbon, R. Kopold, D. B. Milosevic, G. G. Paulus and H. Walther, Advances in Atomic Molecular and Optical Physics, Vol. 48, 2002, pp. 35-98. http://dx.doi.org/10.1016/S1049-250X(02)80006-4
- R. R. Freeman, P. H. Bucksbaum, H. Milchberg, S. Darack, D. Schumacher and M. E. Geusic, Physical Review Letters, Vol. 59, 1987, pp. 1092-1095. http://dx.doi.org/10.1103/PhysRevLett.59.1092
- C. de Boor, “A Practical Guide to Splines,” SpringerVerlag, New York, 1978. http://dx.doi.org/10.1007/978-1-4612-6333-3
- H. Bachau, E. Cormier, P. Decleva, J. E. Hansen and F. Martin, Reports on Progress in Physics, Vol. 64, 2001, pp. 1815-1943. http://dx.doi.org/10.1088/0034-4885/64/12/205
- S. Laulan and H. Bachau, Physical Review A, Vol. 68, 2003, Article ID: 013409. http://dx.doi.org/10.1103/PhysRevA.68.013409
- S. Laulan and H. Bachau, Physical Review A, Vol. 69, 2004, Article ID: 033408. http://dx.doi.org/10.1103/PhysRevA.69.033408
- E. Foumouo, S. Laulan, B. Piraux and H. Bachau, Journal of Physics B, Vol. 39, 2006, pp. S427-S435.
- B. E. A. Saley and M. C. Teich, “Fundamendals of Photonics,” John Wiley and Sons Inc., Hoboken, 2007.
NOTES
*Corresponding author.

