Journal of Modern Physics
Vol.4 No.6A(2013), Article ID:33567,5 pages DOI:10.4236/jmp.2013.46A002
Positive Field-Cooled Susceptibility in Multiply Connected Type-I Superconductors
Physics Department “E. R. Caianiello”, University of Salerno, Fisciano, Italy
Email: rdeluca@unisa.it
Copyright © 2013 Roberto De Luca. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 19, 2013; revised April 21, 2013; accepted May 18, 2013
Keywords: Paramagnetic Meissner Effect; Non-Simply Connected Superconductors; Magnetic Susceptibility
ABSTRACT
A detailed analysis of the magnetic response of field-cooled type-I superconducting hollow cylinders shows that the so-called “paramagnetic Meissner effect” can take place in opportunely devised multiply connected superconductors. Adopting simple circuital analogs of the latter superconducting systems, the magnetic susceptibility of micro-cylinders with one or two holes is studied by means of energy considerations.
1. Introduction
Expulsion of magnetic field from the inner region of simply connected type-I superconductors was first observed by Walther Meissner and Robert Ochsenfeld in 1933, 22 years after the discovery of superconductivity [1]. The two German scientists showed that these superconducting systems, when cooled below the corresponding critical temperature Tc in the presence of low magnetic fields, behaved like perfect diamagnetic materials. With the discovery of high-Tc superconductivity in layered perovskites by Johannes Bednorz and Karl Müller [2] the magnetic properties of these novel superconducting systems were analyzed in detail, starting from the end of 1980’s up to the beginning of 1990’s. In particular, much attention was devoted to the so called “paramagnetic Meissner Effect” (PME), also known as “Wohlleben effect” [3] first reported by a group of German researchers in 1993. In this apparently contradictory definition of the observed phenomenon, the field-cooled susceptibility of high-Tc granular superconductors was observed to be positive for low measuring fields. It thus became evident that the polycrystalline structure in sintered high-Tc materials could play a role in explaining this experimental outcome [4]. In fact, considering sintered superconducting systems as a collection of weakly coupled micrometer sized granules [5], one can describe the magnetic properties of granular superconductors by means of equivalent networks of Josephson junctions [6]. In order to grasp the fundamental mechanisms by which PME might arise, a very simple multiply connected system was studied: a type-I superconducting hollow cylinder [7]. It was shown that the magnetic response of this system exhibits a diamagnetic character for most values of the measuring field magnitude H, while it may give a positive value of the field-cooled susceptibility for welldefined intervals of the applied magnetic flux, if the normal fraction, defined as the ratio between the volume of the hole and the total volume of the sample, is greater than 1/2.
In the present work, after having briefly recalled the results obtained for the hollow cylinder, we study the field-cooled magnetic behavior of multiply connected superconductors consisting of type-I superconducting cylinders in which two holes are present. By adopting a simple circuital model and by taking into account the mutual coefficient between the circuits representing the current loops in the system, we derive a method to calculate the field-cooled magnetic susceptibility of multiply connected type-I superconducting cylinders.
2. A Hollow Superconducting Cylinder
Let us first consider the hollow superconducting cylinder shown in Figure 1. If a uniform magnetic field of constant magnitude H is applied along the cylindrical axis, the current distribution can be simplified as follows: an external shielding current IS flows in the outer surface of the cylinder; a second current I1 shields the inner part of the superconductor from the field h inside the hole.
By applying Ampere’s law, following path CS, and by noticing that the magnetic induction in the superconducting region is zero, we can write
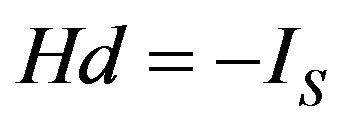 , (1)
, (1)
where d is the height of the cylinder and CS goes through the superconductor in a region sufficiently far from the outer surface. The latter hypothesis is necessary in order to avoid considering the decaying magnetic field inside the superconductor, due to the existence of finite penetration lengths in these materials [1]. We also neglect demagnetization effects due to the finite size of the cylinder. Similarly, applying Ampere’s law and following path C1, we can write
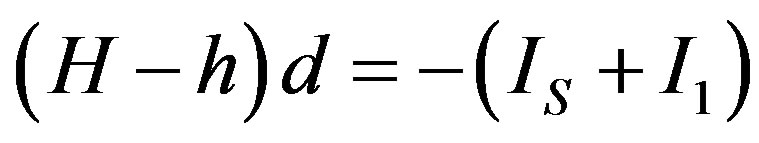 . (2)
. (2)
By now applying (1), we see that Equation (2) reduces to the following:
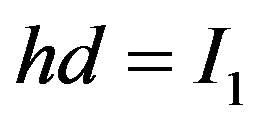 . (3)
. (3)
Let us now write down the magnetic energy EM due to the circulating currents as follows:
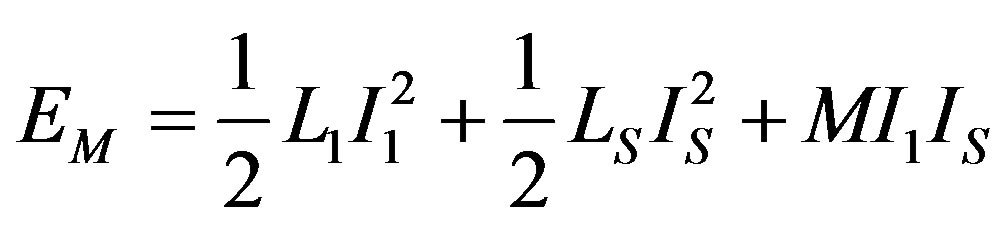 , (4)
, (4)
where, denoting the permeability of vacuum as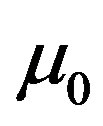 ,
,
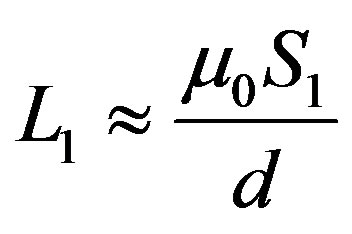 and
and 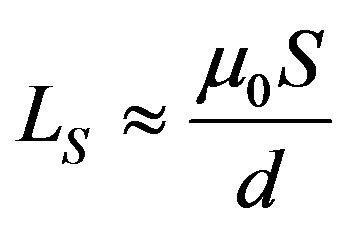 are the inductance coefficients pertaining to the two virtual loops followed by
are the inductance coefficients pertaining to the two virtual loops followed by  and
and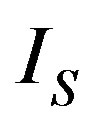 , respectively, and M is the mutual inductance coefficient between these same loops. By taking
, respectively, and M is the mutual inductance coefficient between these same loops. By taking 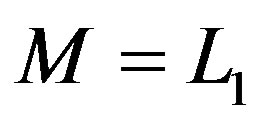 and by substituting Equations (1)-(3) into Equation (4), we have:
and by substituting Equations (1)-(3) into Equation (4), we have:
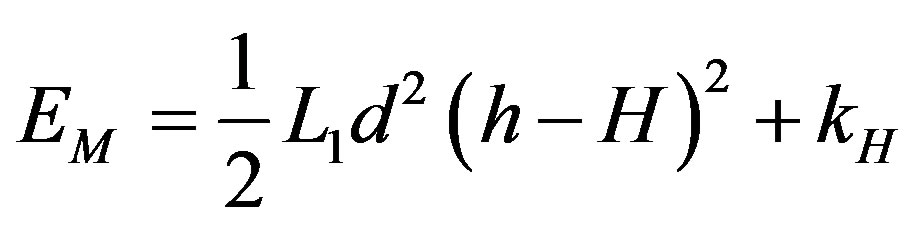 , (5)
, (5)
where 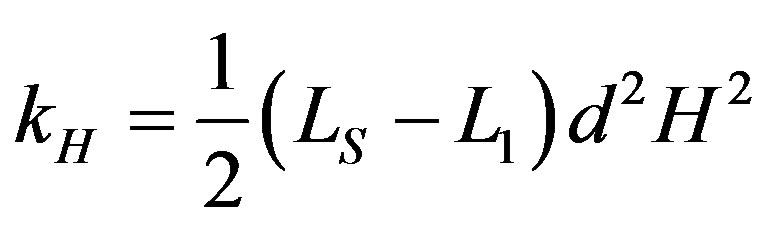 is a constant. By now introducing the flux numbers
is a constant. By now introducing the flux numbers  and
and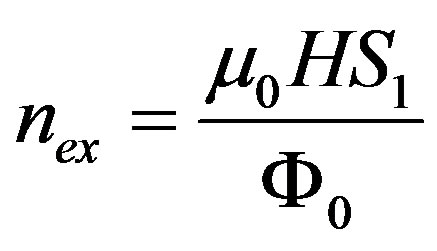 ,
, 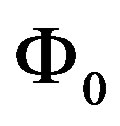 being the elementary flux quantum, we can rewrite Equation (5) in the following final form:
being the elementary flux quantum, we can rewrite Equation (5) in the following final form:
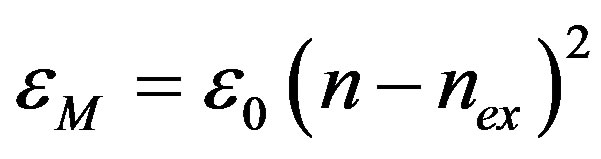 , (6)
, (6)
where 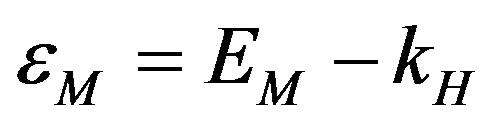 and
and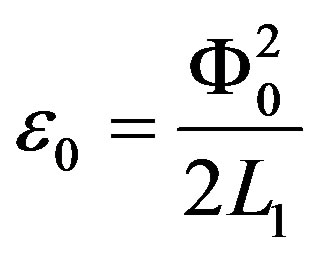 . The possible quantized values of the trapped field in a field cooling experiment has been given by Goodman and Deaver in 1970 [8]. The experimental results reported by these researchers can be summarized by the following simple non-linear expression:
. The possible quantized values of the trapped field in a field cooling experiment has been given by Goodman and Deaver in 1970 [8]. The experimental results reported by these researchers can be summarized by the following simple non-linear expression:
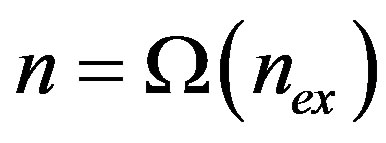 , (7)
, (7)
where the function Ω, when applied to a real number x, gives the closest integer to x. This function can be easily interpreted by considering the minima of the energy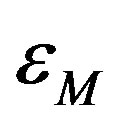 . In fact, by fixing the value of the applied flux number
. In fact, by fixing the value of the applied flux number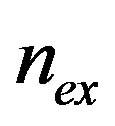 , the system arranges itself in the quantized flux state with n trapped fluxons inside the hole of area S1 in such a way to minimize the energy
, the system arranges itself in the quantized flux state with n trapped fluxons inside the hole of area S1 in such a way to minimize the energy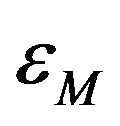 . In this way, only the lower parts of all parabolas in (6) are chosen as possible magnetic state in the system. The result of this procedure, by which one chooses the possible magnetic energy states as
. In this way, only the lower parts of all parabolas in (6) are chosen as possible magnetic state in the system. The result of this procedure, by which one chooses the possible magnetic energy states as  varies, is shown in Figure 2.
varies, is shown in Figure 2.
Having specified the value of the flux number n in (7), the field distribution inside the cylinder can be summarized as follows:
 (8)
(8)
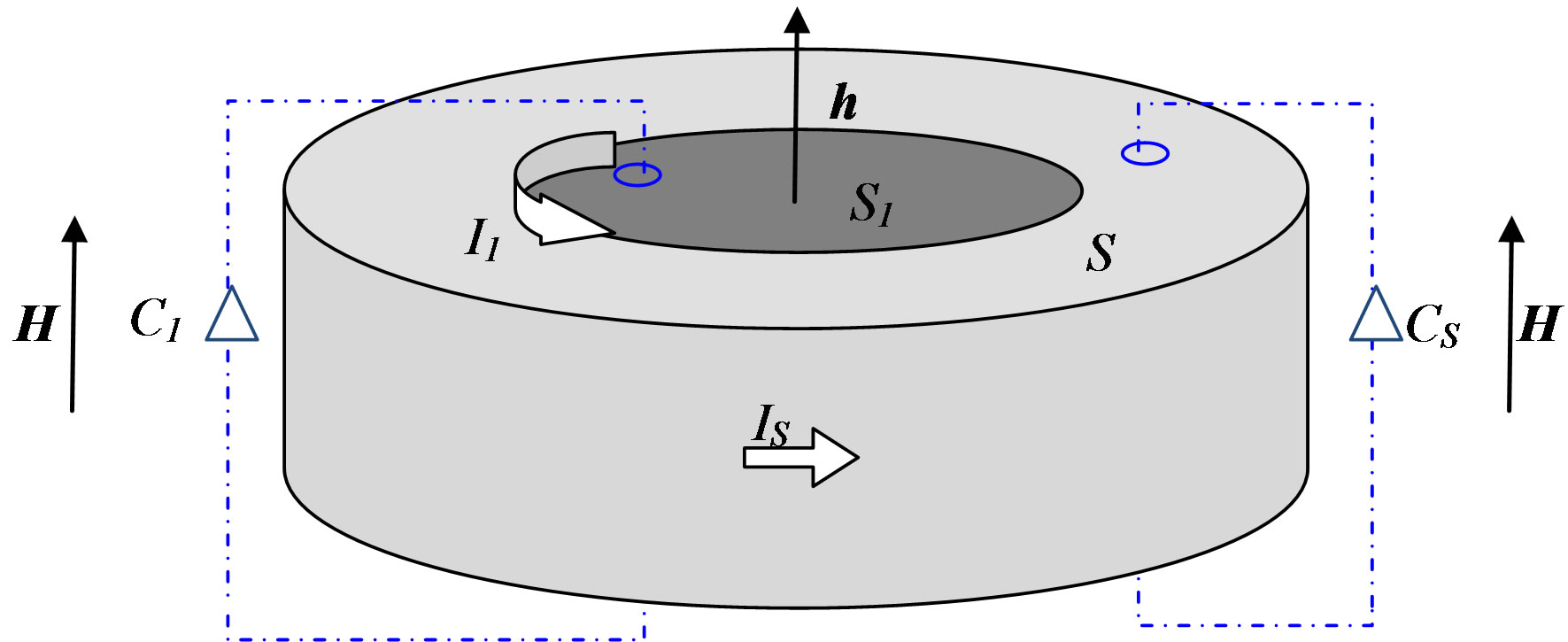
Figure 1. Current distribution in a hollow superconducting cylinder of total cross section S. An axial magnetic field H is applied to the whole system and a magnetic field induction h is present in the hole of section S1. The current IS shields the outer superconducting region from the external magnetic field H, while the current I1 shields the inner superconducting region from the trapped field h. Two different paths, C1 and CS, are shown.
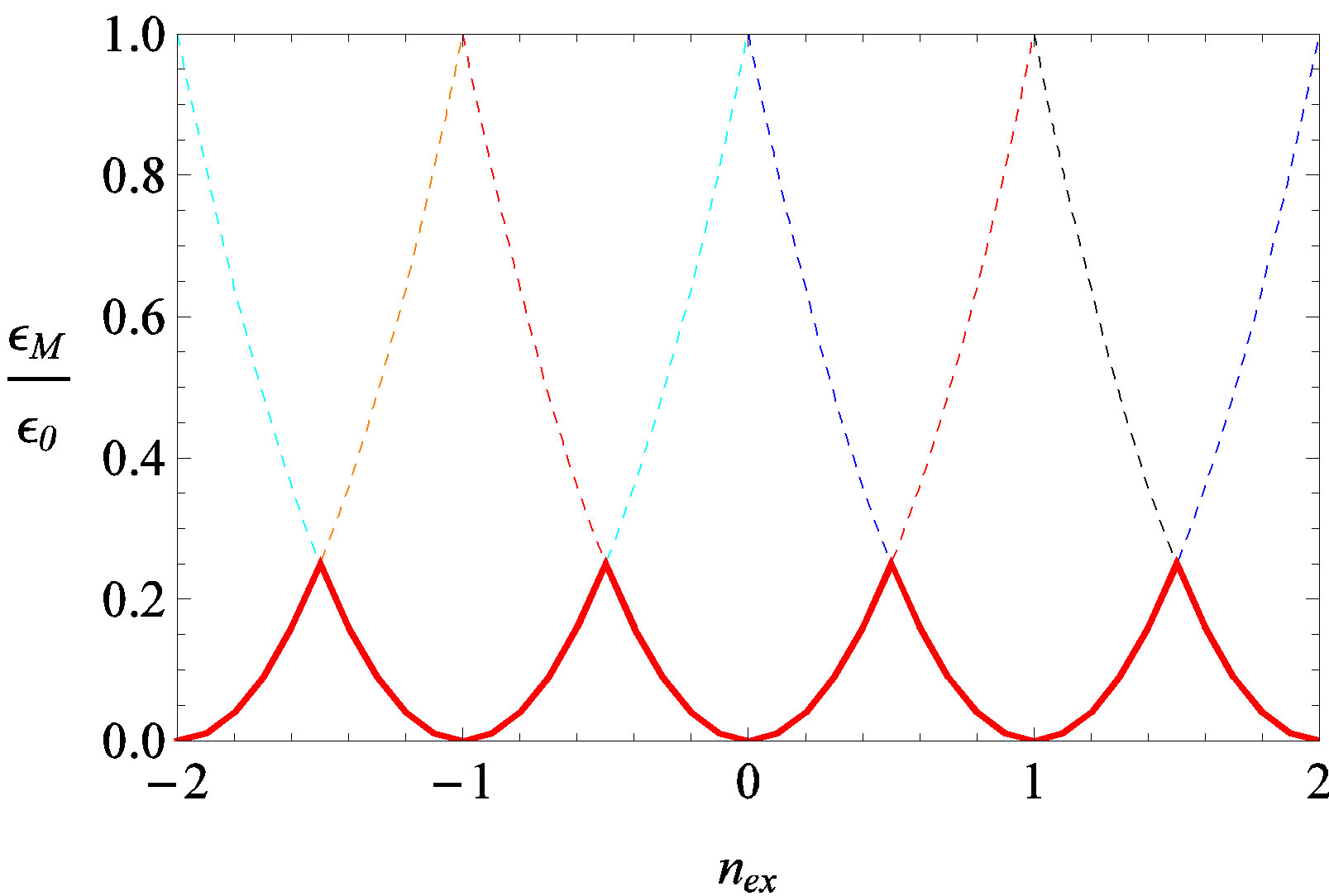
Figure 2. Magnetic energy states in the hollow superconducting cylinder cooled in the presence of a constant measuring field H. These low-lying states are shown as a collection of points on the red full-line curve. The parabolas 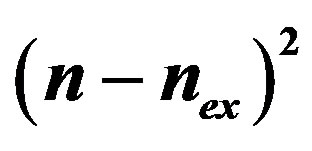 are shown as dashed lines for the following values of n: n = 0 (red); n = 1 (blue); n = −1 (cyan); n = 2 (black), n = −2 (orange). The red full line curve is therefore the result of a minimization procedure over all possible nstates, for fixed
are shown as dashed lines for the following values of n: n = 0 (red); n = 1 (blue); n = −1 (cyan); n = 2 (black), n = −2 (orange). The red full line curve is therefore the result of a minimization procedure over all possible nstates, for fixed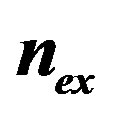 .
.
In order to determine the field-cooled susceptibility
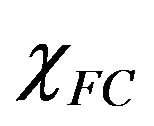 , we need to find the average value
, we need to find the average value 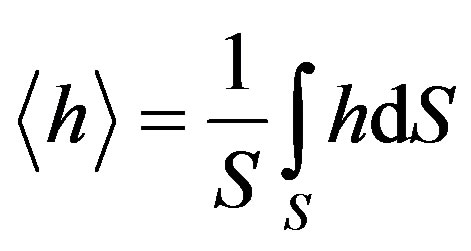 of the magnetic induction inside the hollow cylinder. By applying (8), we find
of the magnetic induction inside the hollow cylinder. By applying (8), we find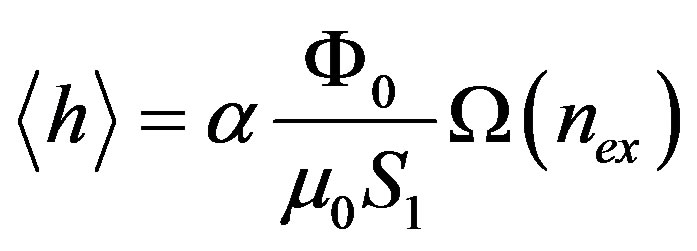 , where
, where 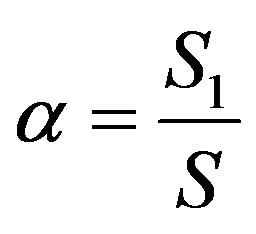 is the normal fraction of the sample. Therefore, by setting the field-cooled magnetic susceptibility equal to
is the normal fraction of the sample. Therefore, by setting the field-cooled magnetic susceptibility equal to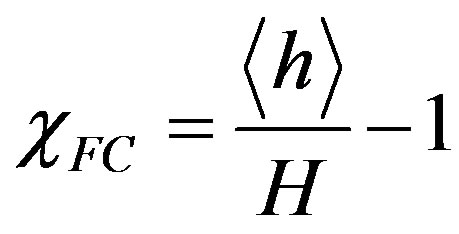 , we find:
, we find:
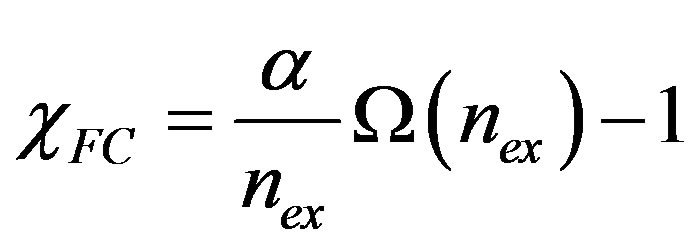 . (9)
. (9)
In Figure 3, we show the field-cooled magnetic susceptibility of a hollow cylinder as a function of the applied flux number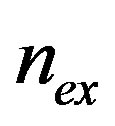 , for various values of the normal fraction α. From Equation (9) we notice that, for α < 1/2, the curves are always below the horizontal axis, so that the magnetic response is always diamagnetic, as it can be also argued from Figure 3. However, for α > 1/2, positive values of
, for various values of the normal fraction α. From Equation (9) we notice that, for α < 1/2, the curves are always below the horizontal axis, so that the magnetic response is always diamagnetic, as it can be also argued from Figure 3. However, for α > 1/2, positive values of 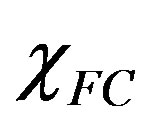 can appear in well-determined
can appear in well-determined 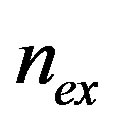
intervals. In fact, by considering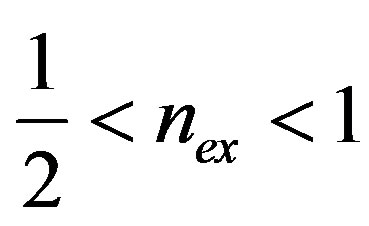 , for which
, for which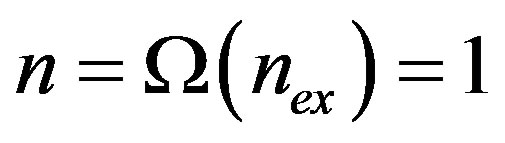 , we have
, we have  if
if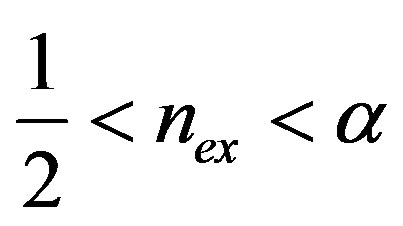 . On the other hand, for
. On the other hand, for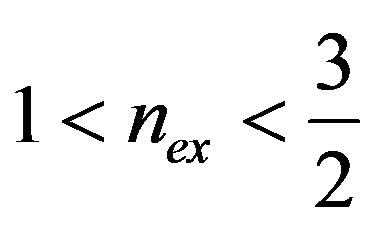 , for which
, for which
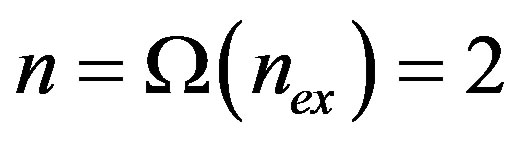 , we cannot have
, we cannot have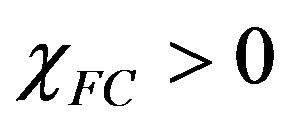 . Therefore, we argue that, for α > 1/2, the only field interval for which
. Therefore, we argue that, for α > 1/2, the only field interval for which 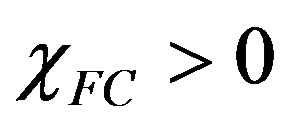 is given by the following simple relation:
is given by the following simple relation:
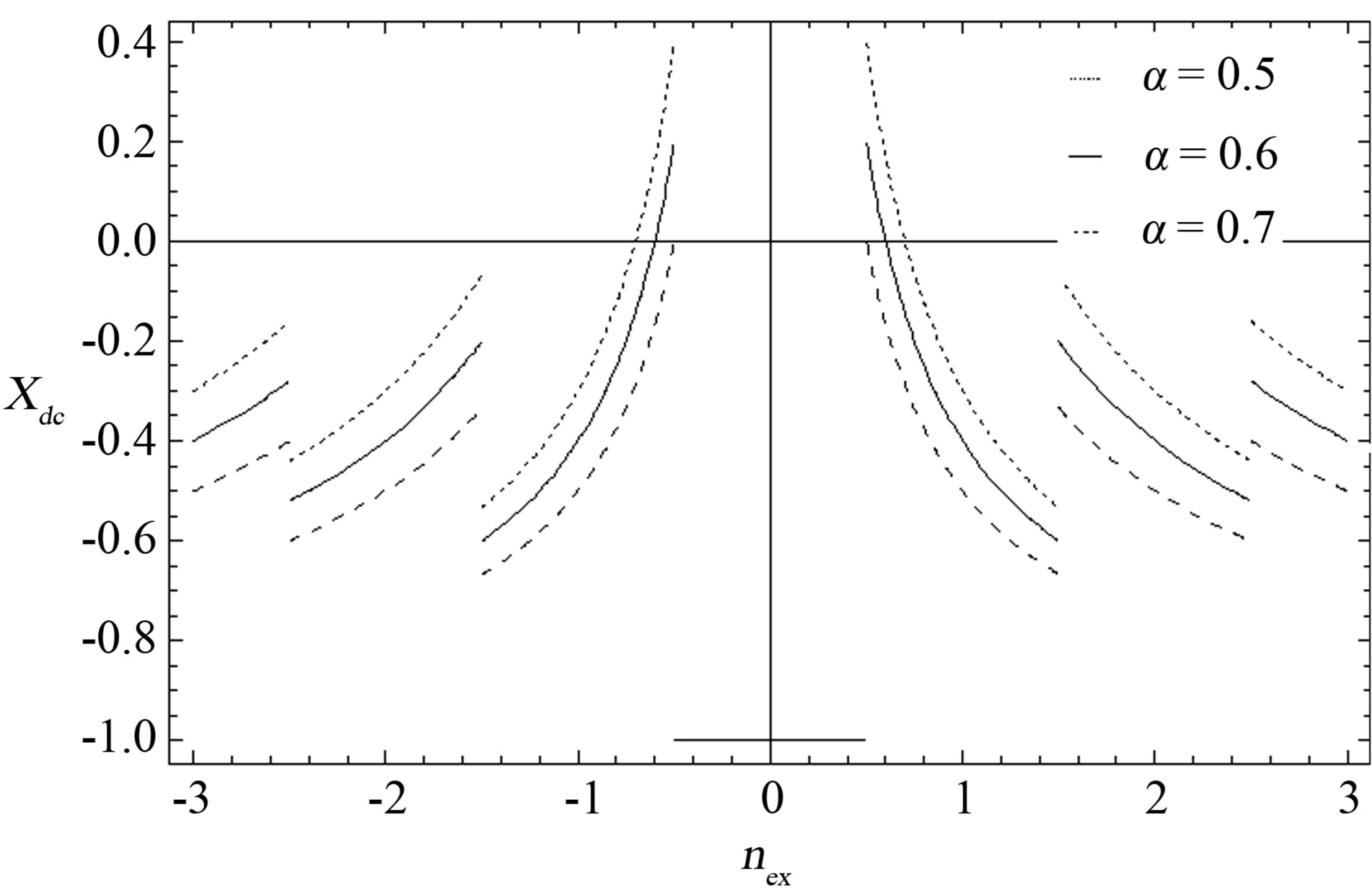
Figure 3. Magnetic susceptibility of a hollow superconducting cylinder cooled in the presence of a constant measuring field H for various values of the normal fraction α, reported in the legend. Depending on the value of the measuring field, the susceptibility may take on positive values for α > 1/2. Susceptibility values in the interval (–1/2,1/2) coincide for all three values of α.
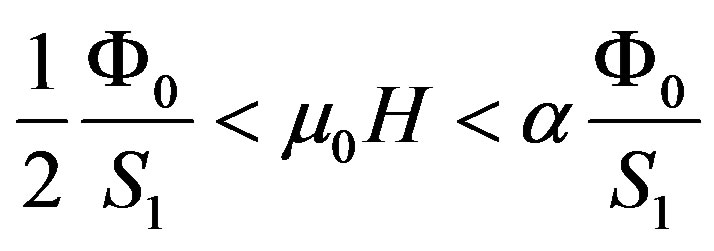 . (10)
. (10)
In order to detect the range in which this effect can be measured, we may notice that in a micro-cylinder (with a hole of inner radius of about 20 μm) the ratio 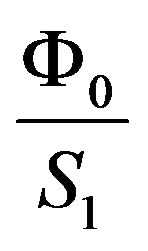 is of 1.64 μT.
is of 1.64 μT.
3. Generalization to a Cylinder with Two Holes
Let us now consider the multiply connected superconductor shown in Figure 4. In this system, consisting of a cylinder of height d and total cross section S with two holes, one of area , the second of area
, the second of area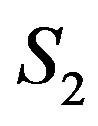 , for a given value of
, for a given value of  different flux numbers can be trapped in each hole (say,
different flux numbers can be trapped in each hole (say, 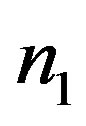 and
and 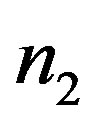 in the holes of area
in the holes of area 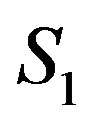 and
and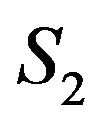 , respectively). Proceeding as in the previous section, by applying Ampere’s law following the three different paths in Figure 4, we find the expressions for the currents and in terms of the various field values, so that we may write:
, respectively). Proceeding as in the previous section, by applying Ampere’s law following the three different paths in Figure 4, we find the expressions for the currents and in terms of the various field values, so that we may write:
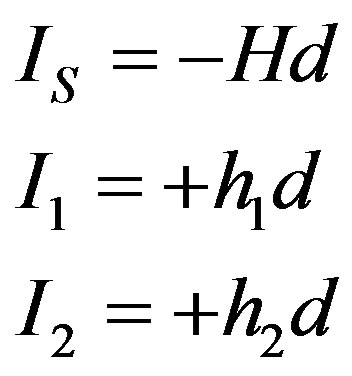 . (11)
. (11)
We may now write down the magnetic energy as follows:
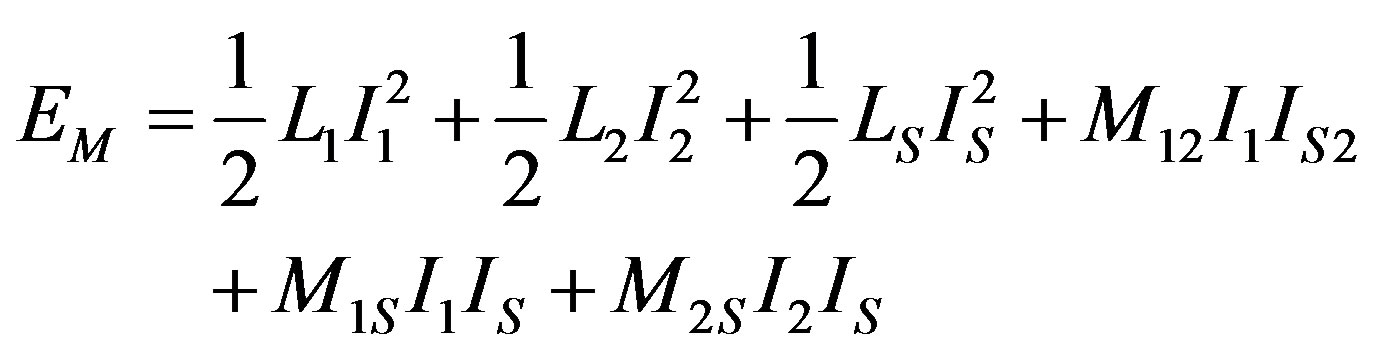 , (12)
, (12)
where the inductance coefficients are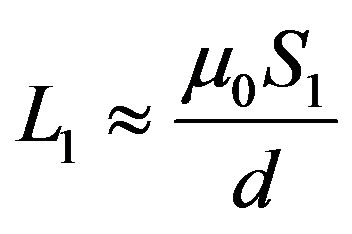 ,
,
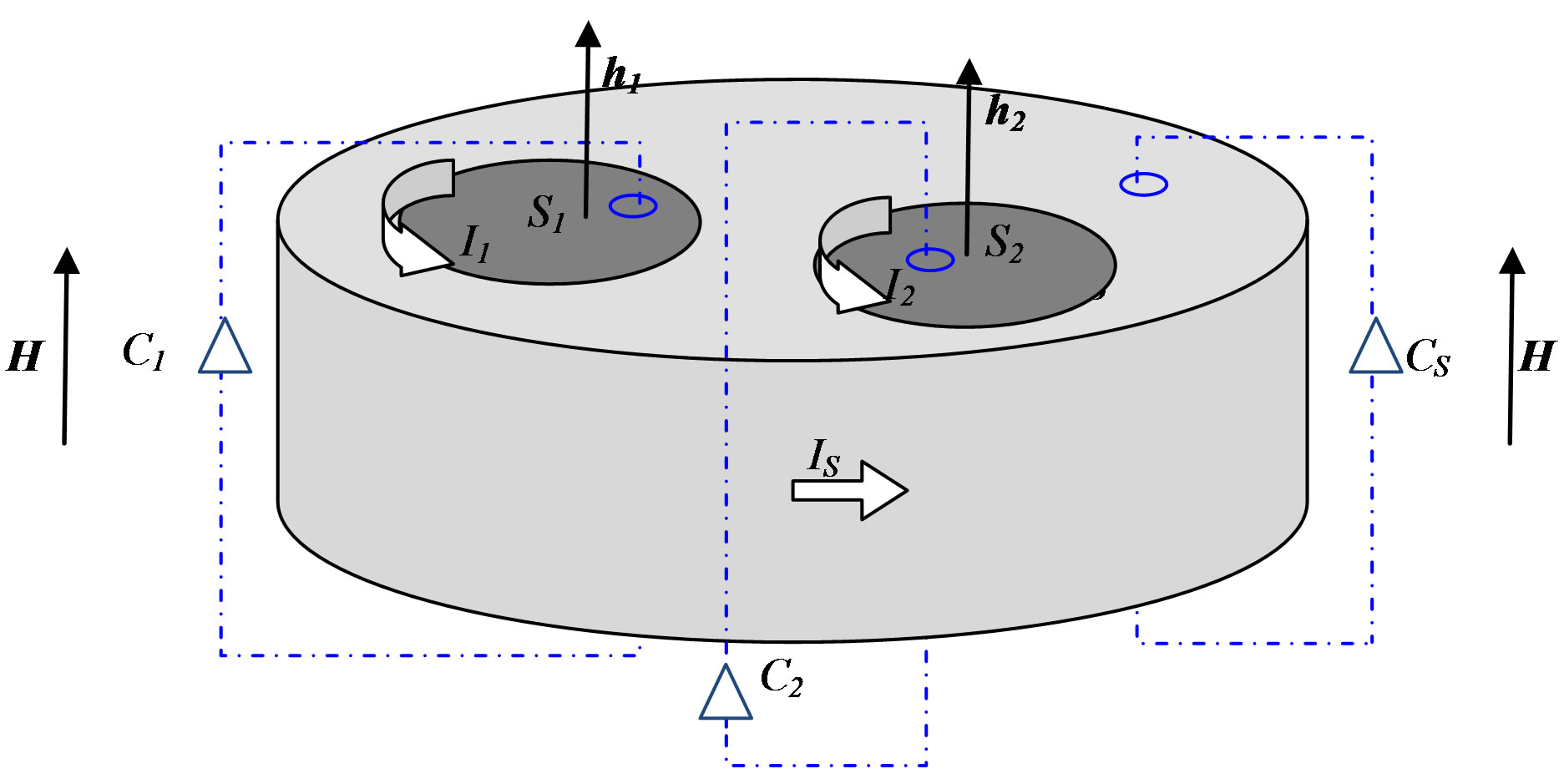
Figure 4. Current distribution in a superconducting cylinder of total cross section S with two holes. An axial magnetic field H is applied to the whole system and magnetic field inductions h1 and h2 are present in the holes of section S1 and S2, respectively. The current IS shields the outer superconducting region from the external magnetic field H, while the currents I1 and I2 shield the inner superconducting region from the trapped fields h1 and h2, respectively. Three different paths, C1, C2, and CS, are shown.
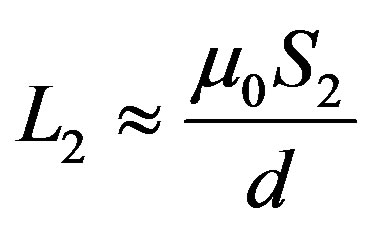 , and
, and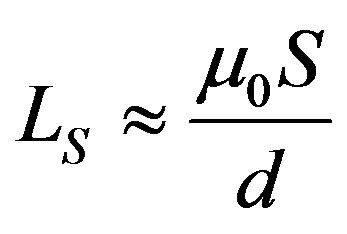 , and where the mutual inductance coefficients between the different current loops are denoted as
, and where the mutual inductance coefficients between the different current loops are denoted as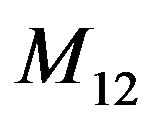 ,
, 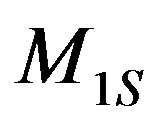 , and
, and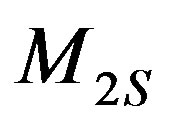 . By proceeding as in the previous section, we define the following flux numbers
. By proceeding as in the previous section, we define the following flux numbers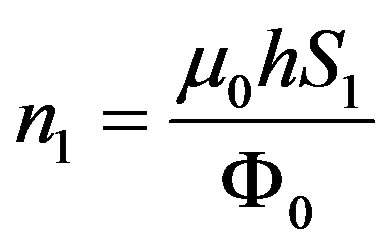 ,
, 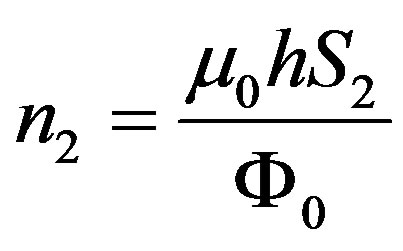 ,
,  , and
, and , with
, with . By now taking
. By now taking 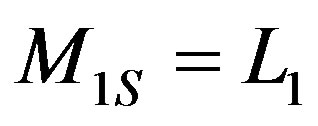 and
and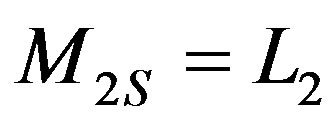 , we may write down the energy
, we may write down the energy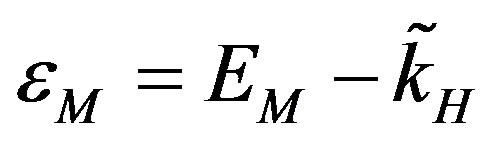 , with
, with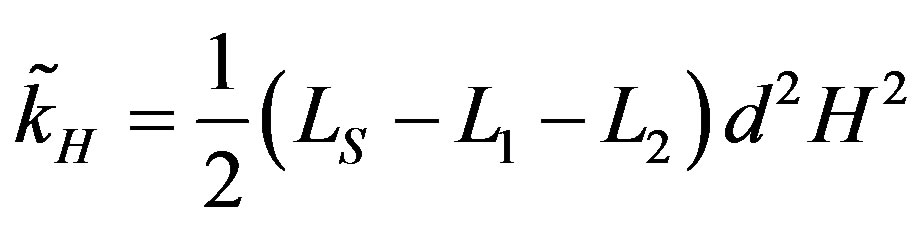 , as follows:
, as follows:
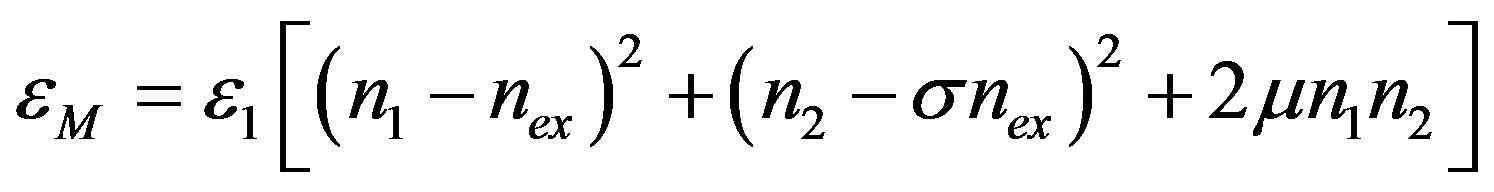 , (13)
, (13)
where 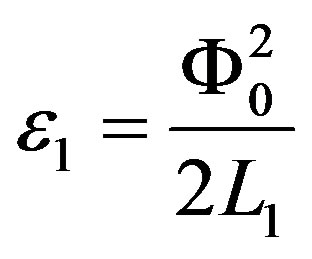 and
and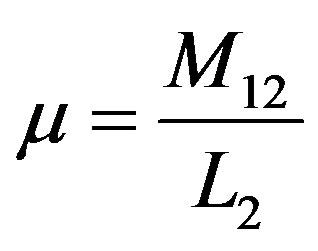 . In Equation (13) we notice that, depending on the choice of
. In Equation (13) we notice that, depending on the choice of  and
and , we obtain different parabolic dependence of
, we obtain different parabolic dependence of 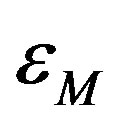 as a function of
as a function of .
.
As before, the magnetic state for a given value of the forcing term 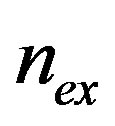 is the one which minimizes the energy
is the one which minimizes the energy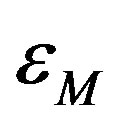 . Therefore, by collecting the different parabolas, we shall choose only the low-lying states at a fixed value of
. Therefore, by collecting the different parabolas, we shall choose only the low-lying states at a fixed value of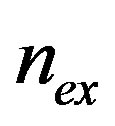 . The representation of these states is given in Figure 5 for
. The representation of these states is given in Figure 5 for 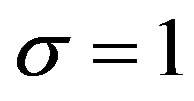 and
and 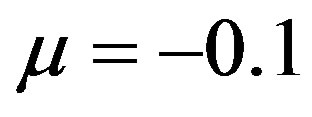 by applying the same minimization procedure explained in the previous section. In the curves in Figure 5 we notice that the presence of the mutual inductance coefficients gives a different shape to
by applying the same minimization procedure explained in the previous section. In the curves in Figure 5 we notice that the presence of the mutual inductance coefficients gives a different shape to
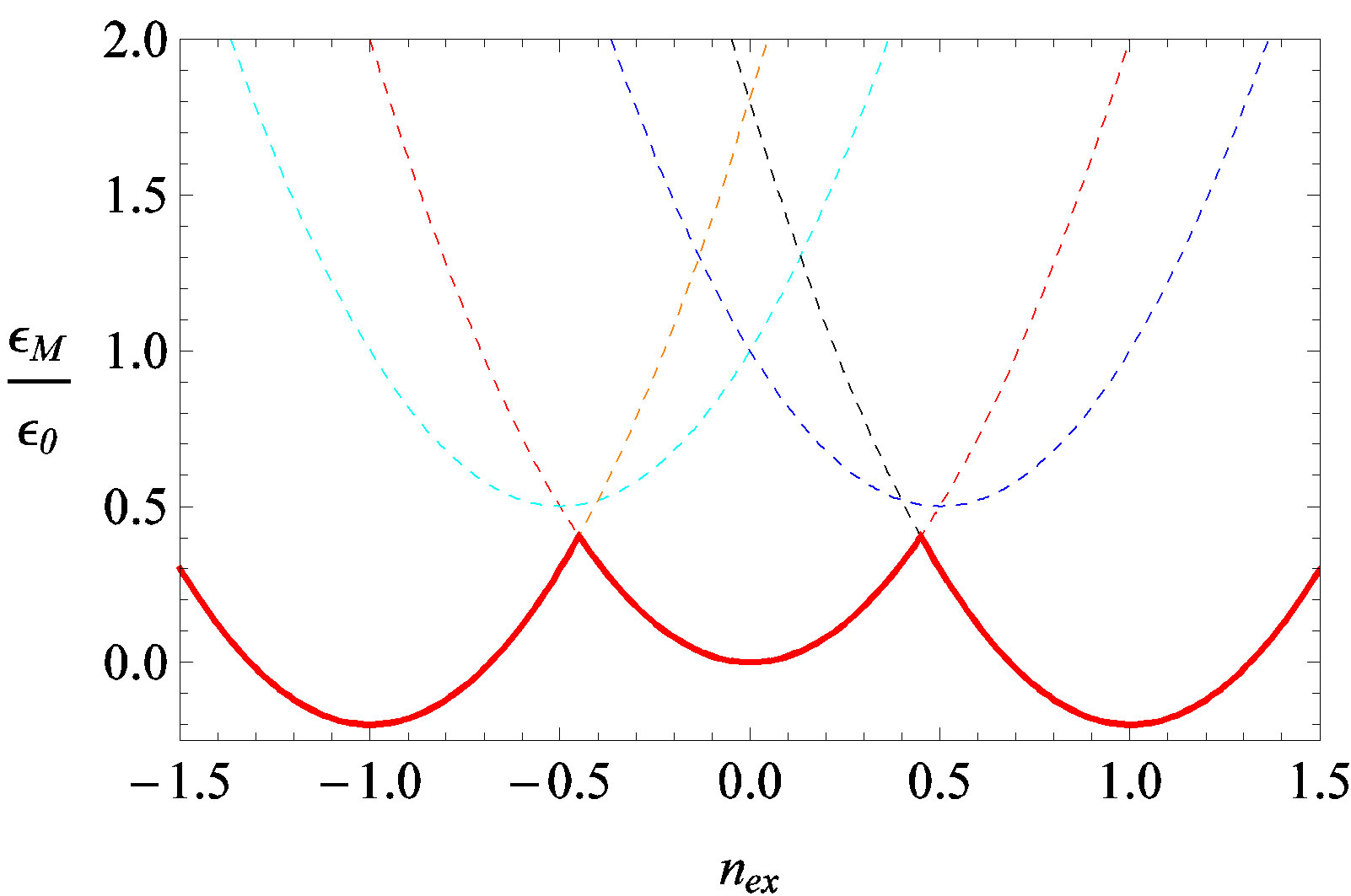
Figure 5. Magnetic energy states in the hollow superconducting cylinder with two holes cooled in the presence of a constant measuring field H. These low-lying states are shown as a collection of points on the red full-line curve. The parabolas 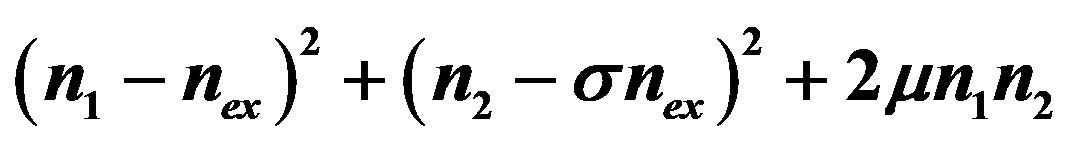 are shown, for
are shown, for 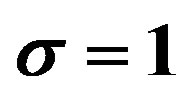 and
and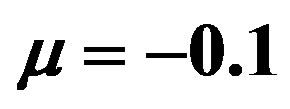 , as dashed lines for the following couples
, as dashed lines for the following couples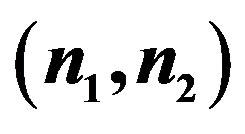 : (0,0) (red); (0,1) (blue); (−1,0)(cyan); (1,1) (black), (−1,−1) (orange). The red full line curve is therefore the result of a minimization process over all possible couples
: (0,0) (red); (0,1) (blue); (−1,0)(cyan); (1,1) (black), (−1,−1) (orange). The red full line curve is therefore the result of a minimization process over all possible couples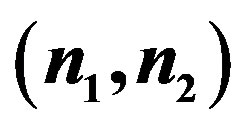 , for fixed
, for fixed 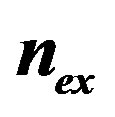 values.
values.
the red curve pertaining to the low-energy states. By a similar algorithm, we can choose to register, for a fixed value of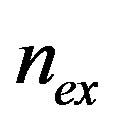 , the couple
, the couple 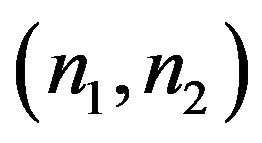 giving the parabola on which the minimum of the energy lies. In this way, by again calculating the average value of the magnetic induction over the whole sample, we define the fieldcooled magnetic susceptibility as follows:
giving the parabola on which the minimum of the energy lies. In this way, by again calculating the average value of the magnetic induction over the whole sample, we define the fieldcooled magnetic susceptibility as follows:
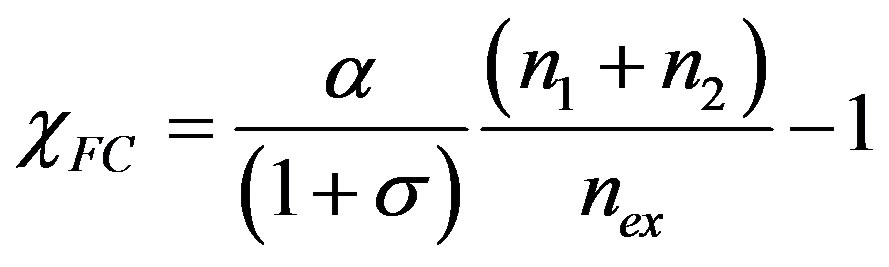 . (14)
. (14)
where now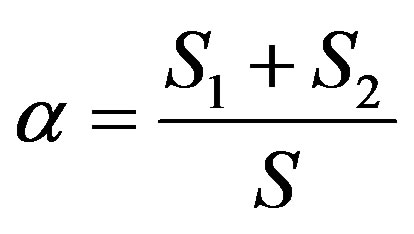 . Therefore, by knowing the quantities
. Therefore, by knowing the quantities 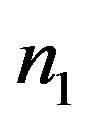 and
and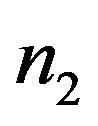 , for a given value of
, for a given value of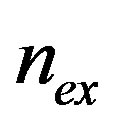 , we can plot the
, we can plot the 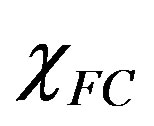 vs.
vs. 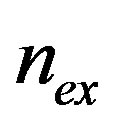 curves.
curves.
By implementing the algorithm for finding the couple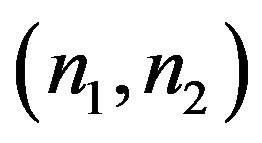 , for a given value of
, for a given value of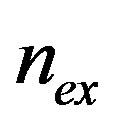 , giving the minimum energy value, we find the
, giving the minimum energy value, we find the 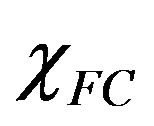 vs.
vs. 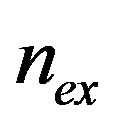 curves in Figures 6(a)-(c).
curves in Figures 6(a)-(c).
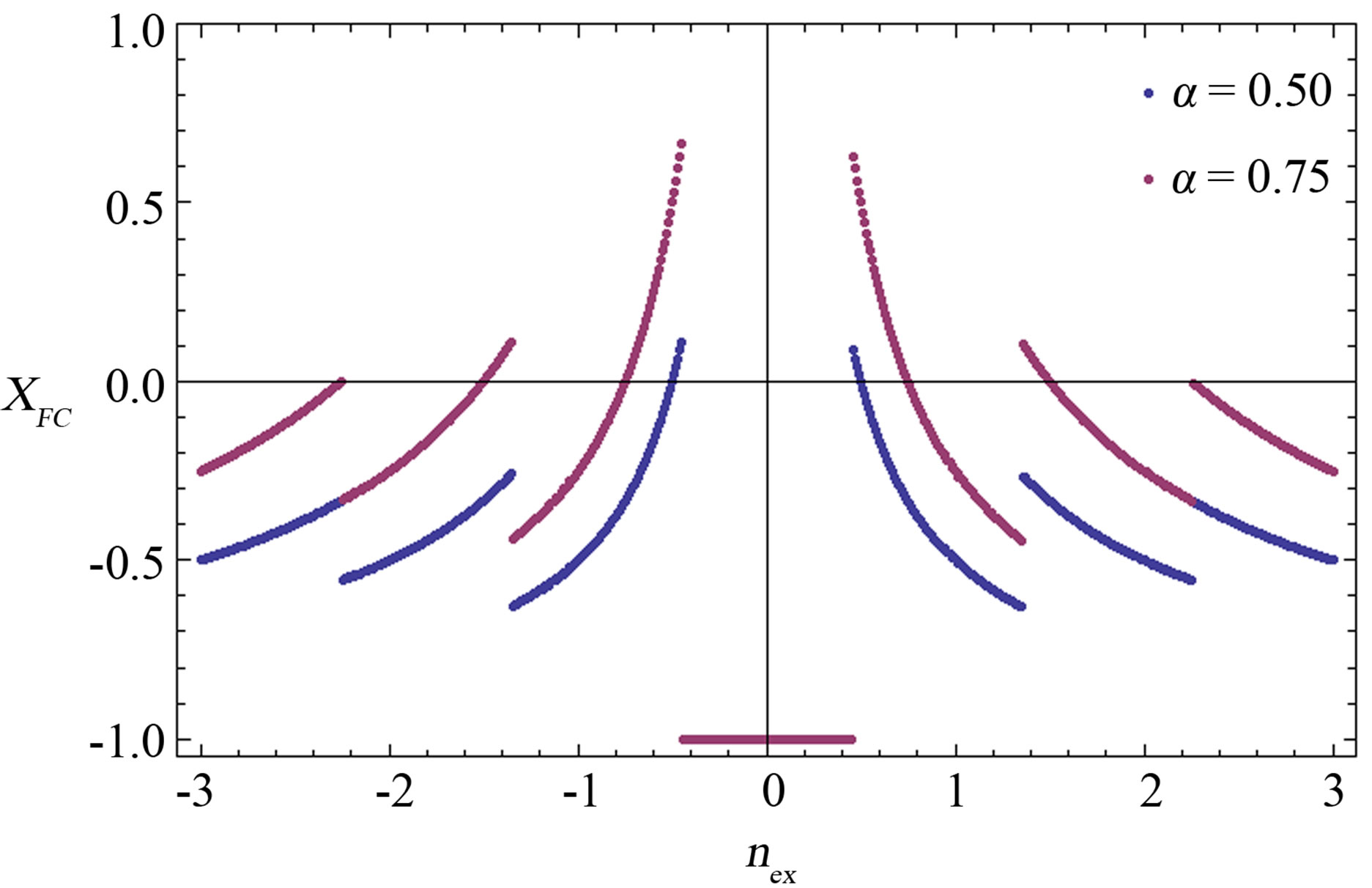
In the curves shown in Figures 6(a)-(c) one notices that the inequality on the minimum value of α giving positive field-cooled susceptibility found in the case of a hollow cylinder with a single hole (namely, α > 1/2) does not hold anymore. In fact, we find intervals of 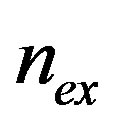 for which
for which 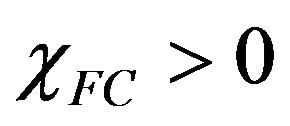 even for α = 1/2, as shown in all three curves in Figures 6(a)-(c). From the same curves it can be argued that, by choosing a more negative value of the mutual inductance coefficient in Figure 6(b), the curves shown in Figure 6(a) rise toward more positive values. On the other hand, when the ratio σ is varied from 1.0 to 0.9, more branches in the
even for α = 1/2, as shown in all three curves in Figures 6(a)-(c). From the same curves it can be argued that, by choosing a more negative value of the mutual inductance coefficient in Figure 6(b), the curves shown in Figure 6(a) rise toward more positive values. On the other hand, when the ratio σ is varied from 1.0 to 0.9, more branches in the 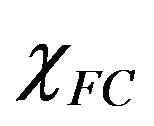 vs.
vs. 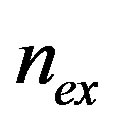 curves appear.
curves appear.
4. Conclusions
The field-cooled magnetic susceptibility 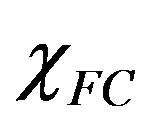 of type-I superconducting hollow cylinders is studied by means of energetic considerations. Starting from the case of a hollow superconducting cylinder with a single hole, we interpret the classical Goodman and Deaver experiment by means of simple concepts on energy minimization. In fact, we see that the magnetic flux trapped inside a hollow superconducting type-I superconductor cooled in the presence of an axial external field of magnitude H can be derived by considering the minima in the magnetic energy states. This energy is written, under elementary assumptions, by considering the magnetic energy generated by the currents flowing in a classical equivalent circuit. In this picture, the superconductor is seen as a perfectly diamagnetic entity. The field cooled magnetic states of the system are described in terms of the applied flux number
of type-I superconducting hollow cylinders is studied by means of energetic considerations. Starting from the case of a hollow superconducting cylinder with a single hole, we interpret the classical Goodman and Deaver experiment by means of simple concepts on energy minimization. In fact, we see that the magnetic flux trapped inside a hollow superconducting type-I superconductor cooled in the presence of an axial external field of magnitude H can be derived by considering the minima in the magnetic energy states. This energy is written, under elementary assumptions, by considering the magnetic energy generated by the currents flowing in a classical equivalent circuit. In this picture, the superconductor is seen as a perfectly diamagnetic entity. The field cooled magnetic states of the system are described in terms of the applied flux number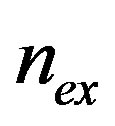 , taken to be proportional to the externally applied field magnitude H.
, taken to be proportional to the externally applied field magnitude H.
By extending this concept to the case of a multiply connected superconductor containing two holes, we are able to derive the  vs.
vs. 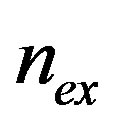 curves, detecting finite
curves, detecting finite
 (a)
(a)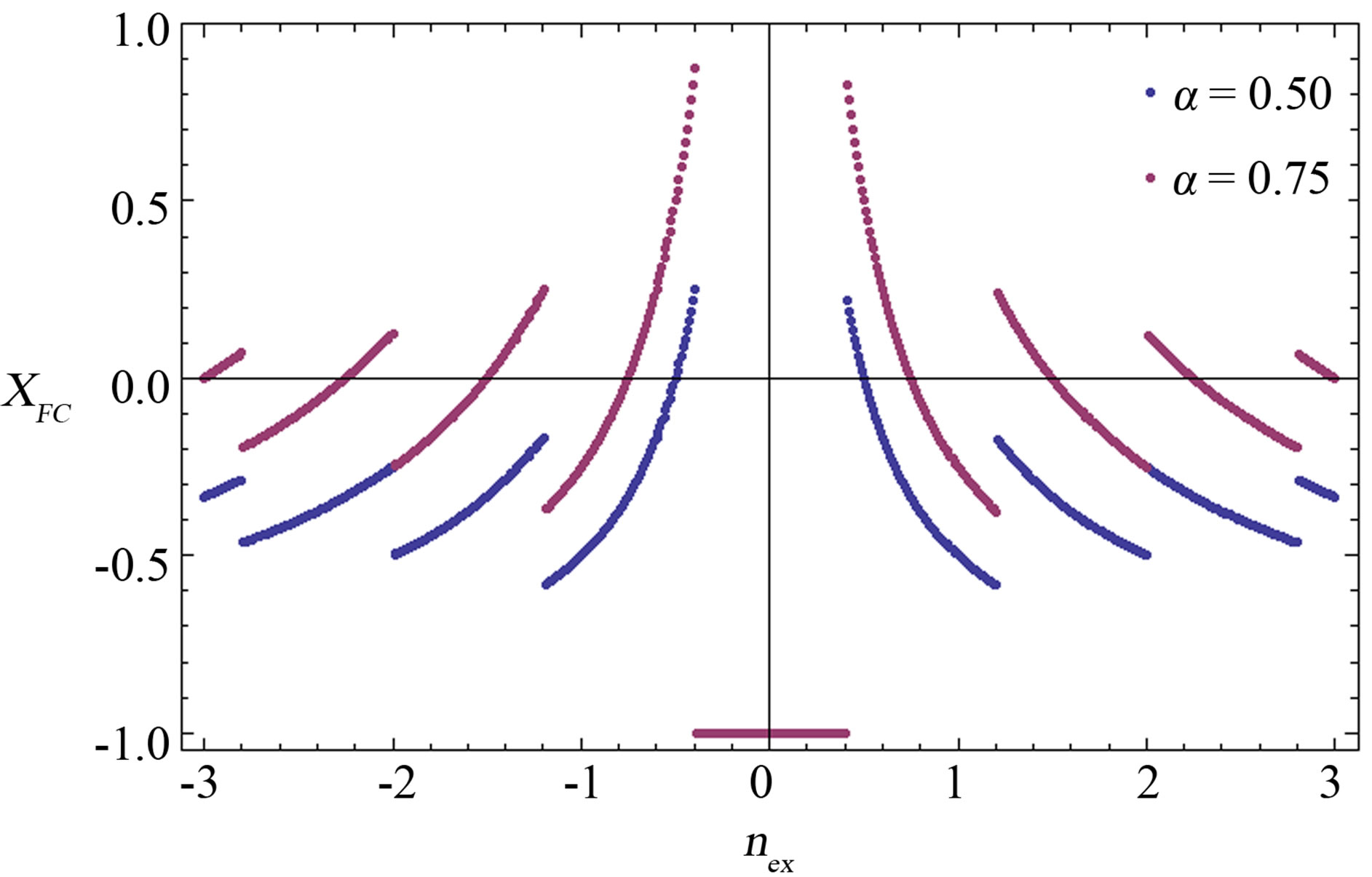 (b)
(b)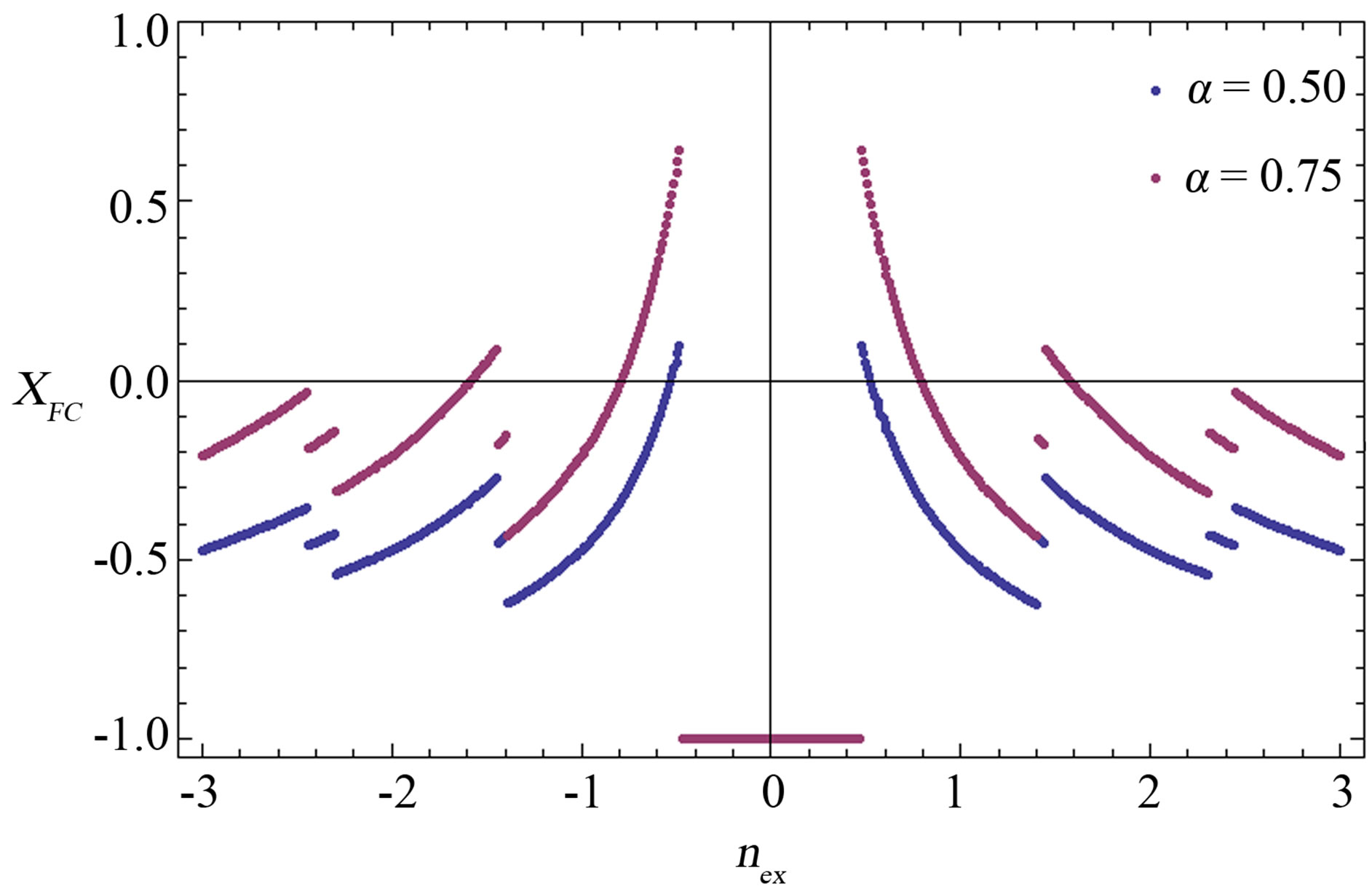 (c)
(c)
Figure 6. Magnetic susceptibility of a hollow superconducting cylinder with two holes cooled in the presence of a constant measuring field H for two values of the normal fraction α, reported in the legend. Depending on the value of the measuring field, the susceptibility may take on positive values. The parameters are chosen as follows: a) 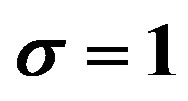 and
and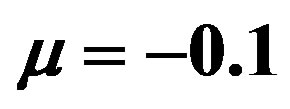 ; b)
; b) 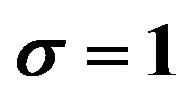 and
and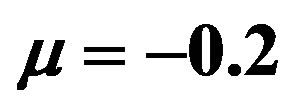 ; c)
; c) 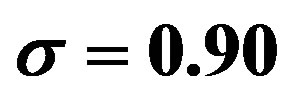 and
and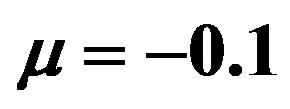 . Susceptibility values in the interval (-1/2,1/2) coincide for the two values of α.
. Susceptibility values in the interval (-1/2,1/2) coincide for the two values of α.
intervals of the field magnitude H in which the susceptibility 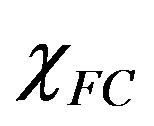 is positive. We therefore argue that in these systems the so called “paramagnetic Meissner effect” is linked to topological as well as to electromagnetic effects.
is positive. We therefore argue that in these systems the so called “paramagnetic Meissner effect” is linked to topological as well as to electromagnetic effects.
REFERENCES
- V. V. Schmidt, “The Physics of Superconductors,” In: P. Muller and A. V. Ustinov, Eds., The Physics of Superconductors, Springer, Berlin, 1997, p. 4.
- J. G. Bednorz and K. A. Müller, Chinese Physics Letters, Vol. 64, 1986, pp. 189-193. doi:10.1007/BF01303701
- W. Braunish, N. Knauf, G. Bauer, A. Kock, A. Becker, B. Freitag, A. Grütz, V. Kataev, S. Neuhausen, B. Roden, D. Khomskii, D. Wohlleben, J. Bock and E. Preisler, Physical Review B, Vol. 48, 1993, p. 4030. doi:10.1103/PhysRevB.48.4030
- K. A. Müller, M. Tagashike and J. G. Bednorz, Physical Review Letters, Vol. 58, 1987, p. 1143. doi:10.1103/PhysRevLett.58.1143
- R. De Luca, Physica C, Vol. 400, 2004, pp. 153-159. doi:10.1016/j.physc.2003.08.002
- R. De Luca, Physica B, Vol. 284-288, 2000, pp. 801-802. doi:10.1016/S0921-4526(99)02101-8
- W. L. Goodman and B. S. Deaver, Physical Review Letters, Vol. 24, 1970, p. 80. doi:10.1103/PhysRevLett.24.870

