Journal of Modern Physics
Vol.4 No.3A(2013), Article ID:29328,8 pages DOI:10.4236/jmp.2013.43A056
Dimensionality Effects in Dipolar Fluids: A Density Functional Theory Study
1Vienna Center for Quantum Science and Technology (VCQ), Technische Universität Wien, Wien, Austria
2Institut für Theoretische Physik, Technische Universität Berlin, Berlin, Germany
Email: rgeiger@ati.ac.at, klapp@physik.tu-berlin.de
Received November 13, 2012; revised December 17, 2012; accepted December 28, 2012
Keywords: Dipole-Dipole Interactions; Dimensionality; Phase Diagram; Density Functional Theory; Long-Range Correlations
ABSTRACT
Using classical density functional theory (DFT) in a modified mean-field approximation we investigate the fluid phase behavior of quasi-two dimensional dipolar fluids confined to a plane. The particles carry three-dimensional dipole moments and interact via a combination of hard-sphere, van-der-Waals, and dipolar interactions. The DFT predicts complex phase behavior involving firstand second-order isotropic-to-ferroelectric transitions, where the ferroelectric ordering is characterized by global polarization within the plane. We compare this phase behavior, particularly the onset of ferroelectric ordering and the related tri-critical points, with corresponding three-dimensional systems, slab-like systems (with finite extension into the third direction), and true two-dimensional systems with two-dimensional dipole moments.
1. Introduction
Two-dimensional (2D) fluids consisting of particles with classical dipole-dipole interactions such as (para)magnetic nanoparticles at interfaces [1-3], cobalt nanocrystals on solid surfaces [4], and suspensions of polarizable colloids in 2D dielectrophoretic set-ups [5,6], currently attract much attention. Indeed, as a result of the directionality of the interactions whose details can be tuned by external (in-plane, out-of-plane, or tilted) fields, 2D dipolar systems display a variety of interesting structures such as chains and bundles at low densities [1,2] but also various solid phases [3]. Especially the self-assembled lowdensity structures suggest that such systems are promising candidates as tunable advanced materials [7] with applications in electrical engineering, sensors [8] and molecular miniature devices.
For theory and computer simulations, exploring the full structural and phase behavior of 2D dipolar systems remains challenging. Apart from the above-mentioned aggregation phenomena, one topic investigated particularly by computer simulations concerns the appearance and characteristics of vapor-liquid transitions [9-14]. Another question touches the structure at high densities close to the range where crystallization is expected to occur. Various Monte Carlo (MC) simulation studies
[9,15] revealed the appearance of ferroelectric (or ferromagnetic, respectively) domains, but overall frustrated (vortex) structures without true long-range orientational ordering. This is consistent with integral equation results [15,16], where predictions on the low-temperature behavior are extracted by analyzing correlation functions. On the other hand, recent Molecular Dynamics (MD) simulations [17] revealed long-range ferroelectric ordering in dense, 2D Stockmayer fluids, where the dipoledipole interactions are supplemented by isotropic Lennard-Jones (LJ) interactions.
Similar to the dense fluid state, the nature of the 2D crystalline structures formed at finite temperatures remains so far unclear [18,19], although ground state calculations indicate ferromagnetism for certain 2D lattice types such as hexagonal lattices [20]. In three-dimensional (3D) systems the existence of long-range ferroelectric (magnetic) ordering under appropriate boundary conditions is well established [21-23]. Moreover, computer simulations of slab-like systems [24], where the particles are confined between two plane-parallel walls, have indicated that this type of confinement can actually promote long-range ordering of the dipole moments, if the wall separation  is sufficiently large. However, decreasing
is sufficiently large. However, decreasing 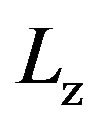 to values where less than three monolayers can form, the ordering seems to disappear [25].
to values where less than three monolayers can form, the ordering seems to disappear [25].
The diversity of simulation results shows that spatial dimension has a profound influence of the ordering behavior of dipolar fluids. The purpose of the present study is to collect and compare theoretical results on that issue based on a relatively simple, mean-field like approach. Specifically, we employ classical density functional theory (DFT) in the modified mean field approximation [26-28], where the pair correlations are replaced by their low-density limit, i.e., the Boltzmann factor. The application of this approach for three-dimensional (3D) dipolar systems and their mixtures [29] was put forward by Groh and Dietrich [30-33], who considered Stockmayer fluids. Later the modified mean-field DFT approach has been used to study confined, slab-like Stockmayer fluids [34,35], with different degrees of sophistication regarding the hard-sphere part of the density functional.
Here we apply the approach to a quasi-2D dipolar (Stockmayer) fluid, where the particles are confined to a plane, but carry 3D dipole moments. Evaluating the phase diagram and comparing with corresponding DFT results for 3D systems, slab-like systems, and true 2D systems with 2D dipole moments we can identify, on a mean-field level, the influence of spatial dimension and of the dimension of the order parameter on global ordering in fluid-like dipolar systems. Based on previous experiences one would expect that the mean-field approach for the quasi-2D system will (as it generally does) overestimate the stability of orientationally ordered phases. However, given the importance of meanfield-like approaches in the general context of spin and dipolar systems, and realizing that the mean-field DFT approach is, so far, still the only theory targeting the whole (homogeneous) phase diagram of dipolar systems, we think our results are important for a complete understanding of such systems.
The remainder of the paper is organized as follows. In Section 2 we formulate the quasi-2D model and briefly detail the derivation of the corresponding grand-canonical functional. Numerical results for the phase diagram at a typical dipole moment are presented in Section 3. There we also use Landau expansions to compare the onset of ordering in the quasi-2D system with the cases of 3D, slab-like and true 2D systems. Finally, in Section 4 we summarize our results.
2. Theory
The quasi-2D Stockmayer fluid consists of disk-like particles of diameter  at positions
at positions 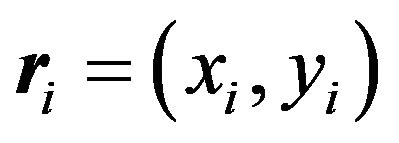 in the x-y plane. The orientation of their 3D dipole moments
in the x-y plane. The orientation of their 3D dipole moments 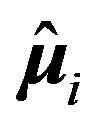 is represented by the Euler angles
is represented by the Euler angles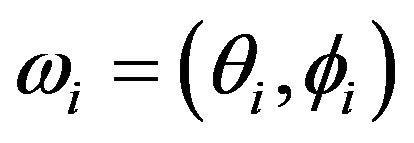 . The microscopic interactions between the particles stem from anisotropic dipole-dipole and isotropic LJ forces. The resulting pair potential between two particles with coordinates
. The microscopic interactions between the particles stem from anisotropic dipole-dipole and isotropic LJ forces. The resulting pair potential between two particles with coordinates 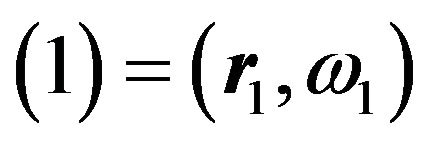 and
and 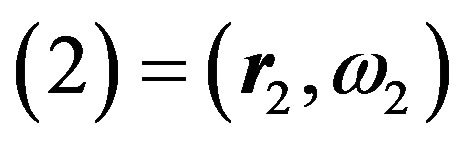 is given as
is given as
 (1)
(1)
where 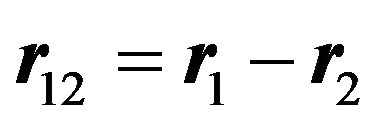 is the connecting vector between the two particles, and
is the connecting vector between the two particles, and . Further,
. Further,
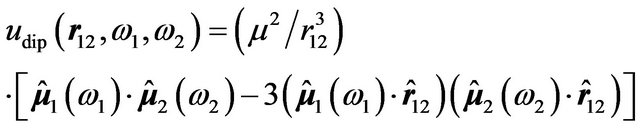
is the 3D dipole-dipole interaction potential, and
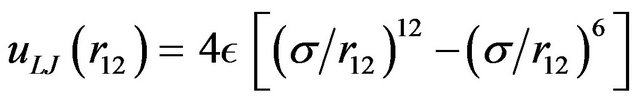 is the LJ potential.
is the LJ potential.
To mimic the fact that the effective range of the 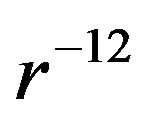 repulsion varies with the thermodynamical parameters, we choose in our DFT calculations a temperaturedependent hard core defined via the Barker-Henderson formula [36], that is,
repulsion varies with the thermodynamical parameters, we choose in our DFT calculations a temperaturedependent hard core defined via the Barker-Henderson formula [36], that is, 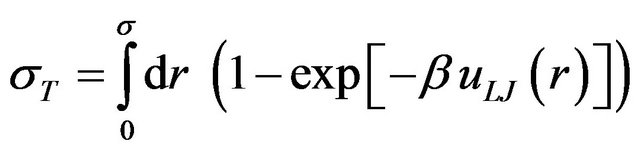 where
where 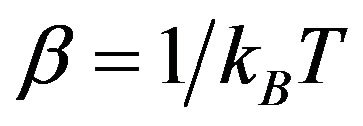 (with
(with 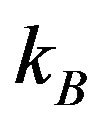 and T being the Boltzmann constant and the temperature, respectively).
and T being the Boltzmann constant and the temperature, respectively).
To analyze the phase behavior we employ classical DFT, where the key quantity is the grand canonical potential  as a functional of the singlet density
as a functional of the singlet density
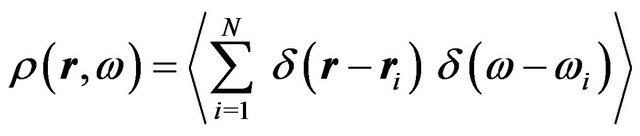 , with N being the total number of particles [37]. We restrict the analysis to fluid-like but possibly polarized ordered phases of the quasi-2D Stockmayer fluid (in the following we assume, without loss of generality, the dipoles to be of electric nature). In principle, investigation of this situation requires to perform a free minimization for the profile
, with N being the total number of particles [37]. We restrict the analysis to fluid-like but possibly polarized ordered phases of the quasi-2D Stockmayer fluid (in the following we assume, without loss of generality, the dipoles to be of electric nature). In principle, investigation of this situation requires to perform a free minimization for the profile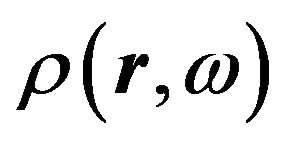 , thereby allowing the system to form domains (or other patterns with spatially varying polarization). Practically, however, minimization including pattern formation is a quite challenging task as demonstrated in [32, 33]. In the present study, where we are interested in the general tendency for ordering, we neglect that problem. That is, we focus on the polarization within a (macroscopically large) fluid domain, which may be part of a globally unpolarized system. We thus consider the singlet density
, thereby allowing the system to form domains (or other patterns with spatially varying polarization). Practically, however, minimization including pattern formation is a quite challenging task as demonstrated in [32, 33]. In the present study, where we are interested in the general tendency for ordering, we neglect that problem. That is, we focus on the polarization within a (macroscopically large) fluid domain, which may be part of a globally unpolarized system. We thus consider the singlet density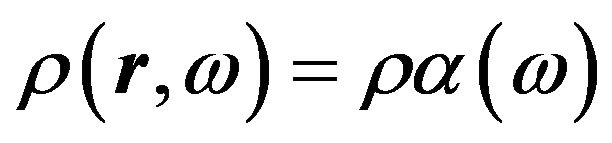 , with
, with  being the constant number density of particles and
being the constant number density of particles and  the orientational distribution function of their dipole moments. This function is normalized to 1 (i.e.,
the orientational distribution function of their dipole moments. This function is normalized to 1 (i.e.,
 ) and equals
) and equals 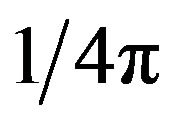 for isotropic states
for isotropic states
[34]. To describe an orientational ordering along a specific direction, we expand the orientational distribution function in terms of spherical harmonics, that is,
 , with the coefficients
, with the coefficients 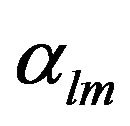 representing orientational order parameters [34]. Nonzero order parameters with
representing orientational order parameters [34]. Nonzero order parameters with  correspond to a macroscopic polarization
correspond to a macroscopic polarization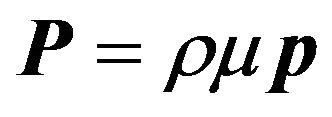 , with
, with
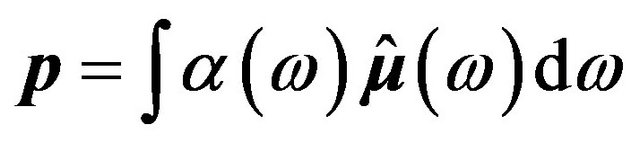 . Indeed, transforming the Cartesian components of
. Indeed, transforming the Cartesian components of 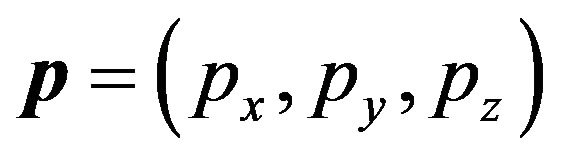 in terms of spherical harmonics one obtains
in terms of spherical harmonics one obtains
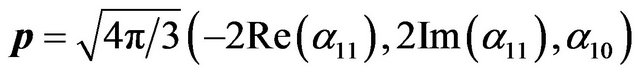 [34]. Similarly, nonzero order parameters
[34]. Similarly, nonzero order parameters 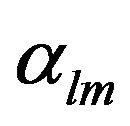 with
with  indicate that there is a preferred orientation of the dipole axes.
indicate that there is a preferred orientation of the dipole axes.
Within the grand canonical formalism, the system is characterized by its size , the chemical potential
, the chemical potential 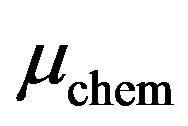 and the inverse temperature
and the inverse temperature . In the present study, the dipolar contribution to the excess (interaction) free energy is treated in the modified mean-field approximation, where the pair correlations are approximated by the Boltzmann factor [26-28]. In addition, following our previous study on slab-like systems [34], we perform a perturbation expansion of the Mayer function and truncate the latter after the quadratic term. Such a truncation has been first employed in a DFT study of the surface tension of polar fluids [26]. Later, results for the phase diagrams of bulk polar fluids [31] have indicated that the second-order theory yields data very close to those from the full modified meanfield approximation (without any truncation). As a consequence of the truncation, the resulting excess free energy contains only terms up to
. In the present study, the dipolar contribution to the excess (interaction) free energy is treated in the modified mean-field approximation, where the pair correlations are approximated by the Boltzmann factor [26-28]. In addition, following our previous study on slab-like systems [34], we perform a perturbation expansion of the Mayer function and truncate the latter after the quadratic term. Such a truncation has been first employed in a DFT study of the surface tension of polar fluids [26]. Later, results for the phase diagrams of bulk polar fluids [31] have indicated that the second-order theory yields data very close to those from the full modified meanfield approximation (without any truncation). As a consequence of the truncation, the resulting excess free energy contains only terms up to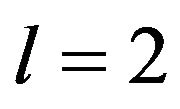 . For a detailed calculation for the quasi-2D case (which proceeds analogous to the slab case) we refer the reader to Ref. [38]. The resulting expression for the grand canonical functional is given by
. For a detailed calculation for the quasi-2D case (which proceeds analogous to the slab case) we refer the reader to Ref. [38]. The resulting expression for the grand canonical functional is given by

(2)
On the right side of Equation (2), the first line contains ideal gas contributions (involving the thermal wavelength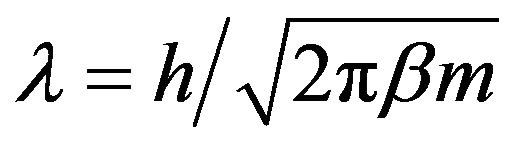 ) and the orientational entropy (last term). The second line contains the excess free energy of our reference system, the hard disk fluid [39], involving the 2D packing fraction
) and the orientational entropy (last term). The second line contains the excess free energy of our reference system, the hard disk fluid [39], involving the 2D packing fraction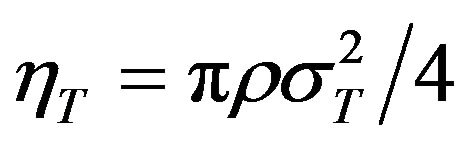 . The three last terms account for the dipolar interactions, where the functions
. The three last terms account for the dipolar interactions, where the functions

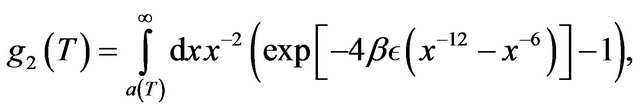
and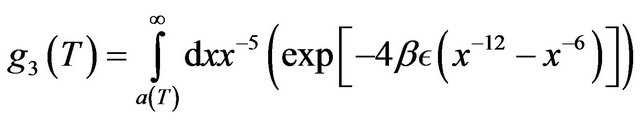 with
with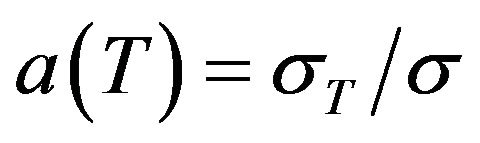 . Finally, in the last term on the right side of Equation (2),
. Finally, in the last term on the right side of Equation (2),
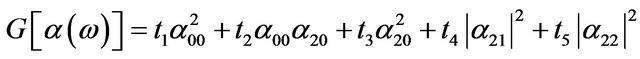 where
where
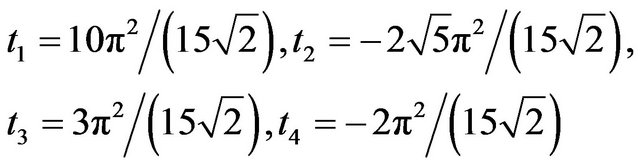
and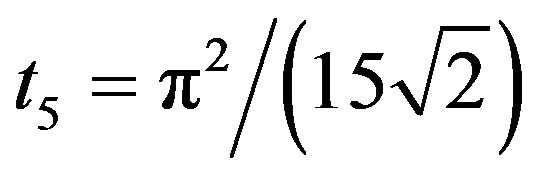 .
.
Minimization of the functional (2) with respect to 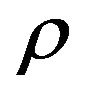 and
and 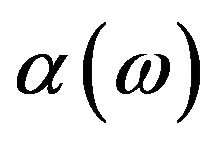 yields the Euler-Lagrange equations for this problem [38]. They consist of a set of nonlinear, coupled equations for the density ρ and the OPs
yields the Euler-Lagrange equations for this problem [38]. They consist of a set of nonlinear, coupled equations for the density ρ and the OPs  appearing in Equation (2). The equations are solved numerically using a Newton-Raphson algorithm [40].
appearing in Equation (2). The equations are solved numerically using a Newton-Raphson algorithm [40].
In the following we characterize the state of the quasi- 2D Stockmayer fluid by the dimensionless density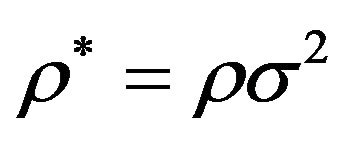 , temperature
, temperature , chemical potential
, chemical potential
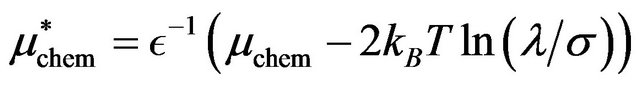 , and dipole moment
, and dipole moment
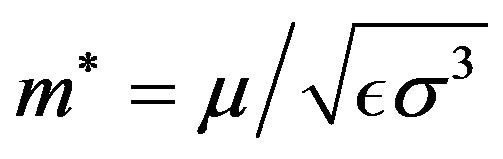 . The quantity
. The quantity 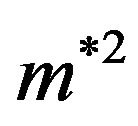 measures the strength of the dipolar interactions in an antiparallel side-by-side configuration relative to the LJ interactions. We note that the coupling parameters
measures the strength of the dipolar interactions in an antiparallel side-by-side configuration relative to the LJ interactions. We note that the coupling parameters  and
and 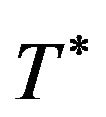 are equivalently defined in 3D (or slit-pore) dipolar systems [34], so that the results can be conveniently compared.
are equivalently defined in 3D (or slit-pore) dipolar systems [34], so that the results can be conveniently compared.
3. Results
Following earlier DFT studies on confined Stockmayer fluids [34] we consider a system characterized by , a typical value for moderately polar molecular fluids such as chloroform [41]. The calculated fluid phase diagram in the density-temperature and chemical potential-temperature plane is shown in Figures 1(a) and (b), respectively. The latter representation better relates to typical sorption experiments [42].
, a typical value for moderately polar molecular fluids such as chloroform [41]. The calculated fluid phase diagram in the density-temperature and chemical potential-temperature plane is shown in Figures 1(a) and (b), respectively. The latter representation better relates to typical sorption experiments [42].
For small and intermediate densities (or chemical potentials) we find a state where all order parameters 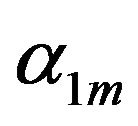 are equal to zero, and those with
are equal to zero, and those with 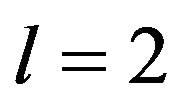 are either zero
are either zero  or negative
or negative . Thus, there is no global polarization and neither a global ordering of the dipole axes; we therefore refer to this state as “isotropic fluid” (IF). The negative values of
. Thus, there is no global polarization and neither a global ordering of the dipole axes; we therefore refer to this state as “isotropic fluid” (IF). The negative values of 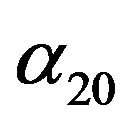 merely indicate that the dipoles tend to avoid to be oriented parallel or antiparallel to the
merely indicate that the dipoles tend to avoid to be oriented parallel or antiparallel to the  -axis; rather they prefer to lie (with random orientations) in the
-axis; rather they prefer to lie (with random orientations) in the 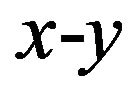 -plane. This is an expected effect in a dilute, quasi-2D dipolar system (consistent with simulations and other theoretical studies,
-plane. This is an expected effect in a dilute, quasi-2D dipolar system (consistent with simulations and other theoretical studies,
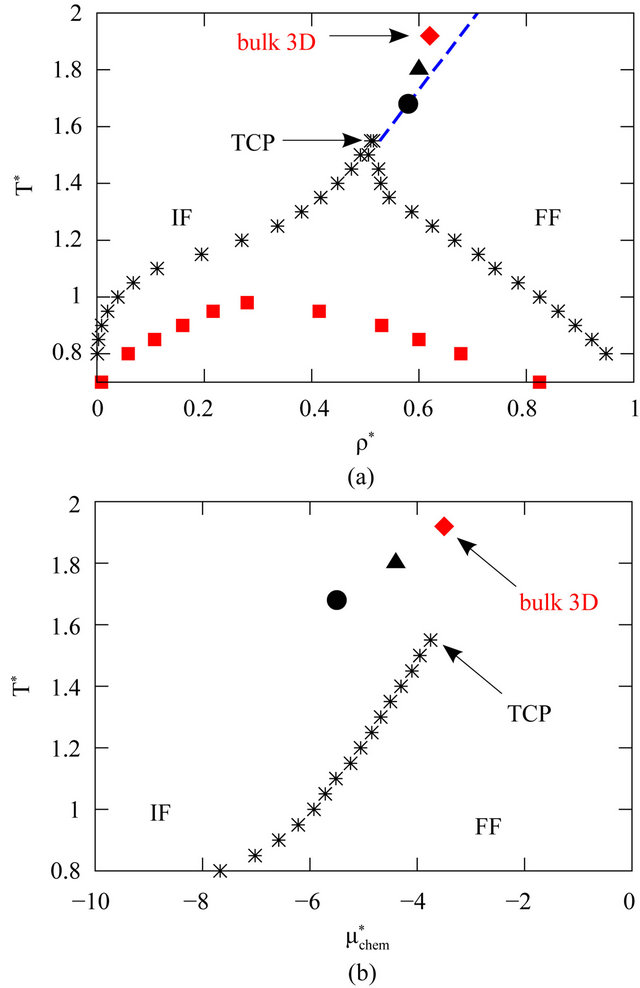
Figure 1. (Color online) (a) Phase diagram of the quasi-2D Stockmayer fluid (m* = 1.5) in the density-temperature plane. The regime under the black stars indicates the IF-FF coexistence region. The blue dashed line is the line of critical points (see Equation (4)), which starts at a tricritical point (TCP). Included are results (from [34]) for the TCPs of the corresponding 3D Stockmayer fluid (red diamonds), and two slit-pore systems with wall separations Lz = 10σ (black triangle) and Lz = 4σ (black circle). The red squares indicate the IG-IL coexistence curve of the quasi-2D system resulting from a separat calculation where the system is forced to be unpolarized; (b) Corresponding phase diagram in the chemical potential-temperature plane.
see e.g. [16]). At higher densities, the system then develops a non-zero polarization, to which we refer to as “ferroelectric fluid” (FF). Within this state, the vector  points along an (arbitrary) direction in the
points along an (arbitrary) direction in the 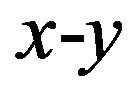 -plane (as reflected by
-plane (as reflected by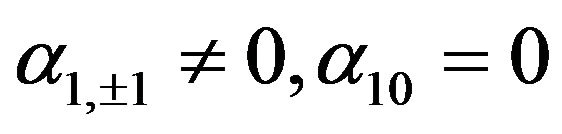 ). Notice that the preference of in-plane polarization (rather than out-of-plane polarization) can already be seen from the prefactor of the corresponding terms
). Notice that the preference of in-plane polarization (rather than out-of-plane polarization) can already be seen from the prefactor of the corresponding terms  in Equation (2).
in Equation (2).
The transition between the IF and the FF phase is discontinuous in  and ρ (yet not in
and ρ (yet not in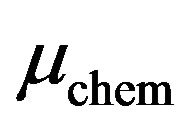 ) for temperatures below a tricritical temperature
) for temperatures below a tricritical temperature 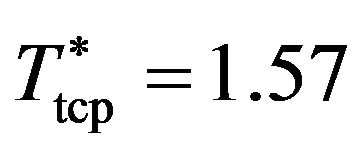 (see
(see
Figure 1(a)). Above the tricritical point (TCP) the transition becomes continuous, which results in a line of critical points. The appearance of a TCP is a typical feature of DFT predictions of the phase diagrams of dipolar fluids [30,31,34] and also Heisenberg fluids [43]. Recent MC studies for 3D dipolar fluids confirm that the transition between isotropic and ferroelectric fluid is of secondorder in a broad range of temperatures [23]. Within the DFT, the line of critical points can be determined from a Landau expansion of the free energy, assuming that the OPs characterizing the FF state are small (i.e.,
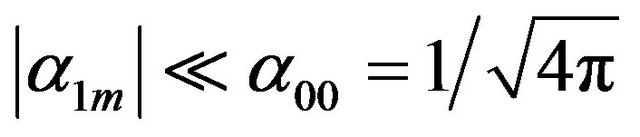 ). To this end we expand the integral
). To this end we expand the integral  in Equation (2)that is, the orientational entropy, in a Taylor serios around the isotropic state (where
in Equation (2)that is, the orientational entropy, in a Taylor serios around the isotropic state (where
 ). Collecting those terms in the resulting approximate functional,
). Collecting those terms in the resulting approximate functional,  , that are proportional to
, that are proportional to , we obtain [38]
, we obtain [38]
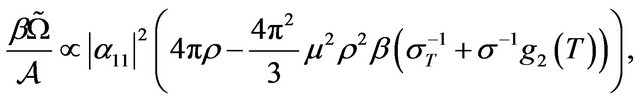 (3)
(3)
where the first term stems from the orientational entropy, whereas the second term results from the interaction free energy in Equation (2). The second order phase transition is characterized by a change of sign of the factor of  in Equation (3). We thus obtain
in Equation (3). We thus obtain
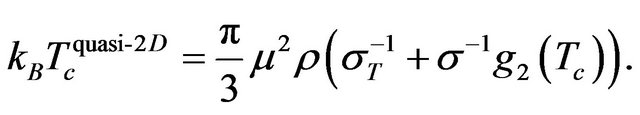 (4)
(4)
This is approximatively the equation of a straight line in the density-temperature plane, consistent with what one sees in Figure 1(a).
In Figures 1(a) and (b) we have included DFT data for tricritical points of Stockmayer fluids in 3D and in slit-pore geometries. Within the latter situation, the particles are confined between two planar, attractive walls separated by a distance 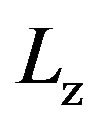 [34]. We note that, both for the 3D and the slab case, our data somewhat differ numerically from those presented in another recent DFT study of confined Stockmayer fluids [35]. This is since we used (contrary to [35]) a temperature-dependent particle diameter and a homogeneous ansatz for the number density in the slit-pore. However, from a qualitative point of view, the observed trends regarding the impact of confinement on the TCP are the same in both studies [34,35]. In particular, both predict that decreasing
[34]. We note that, both for the 3D and the slab case, our data somewhat differ numerically from those presented in another recent DFT study of confined Stockmayer fluids [35]. This is since we used (contrary to [35]) a temperature-dependent particle diameter and a homogeneous ansatz for the number density in the slit-pore. However, from a qualitative point of view, the observed trends regarding the impact of confinement on the TCP are the same in both studies [34,35]. In particular, both predict that decreasing 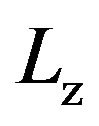 (that is, increasing the degree of confinement) shifts the TCP towards lower temperatures and somewhat lower densities For example, according to [34], the tricritical parameters
(that is, increasing the degree of confinement) shifts the TCP towards lower temperatures and somewhat lower densities For example, according to [34], the tricritical parameters 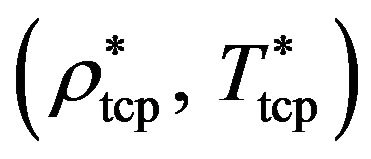 are
are 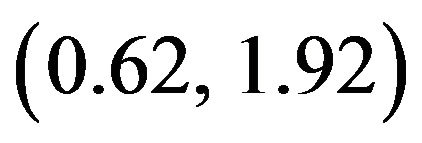 at
at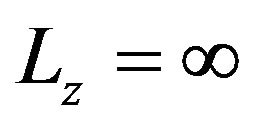 , i.e., in the 3D (bulk) limit,
, i.e., in the 3D (bulk) limit,  at
at 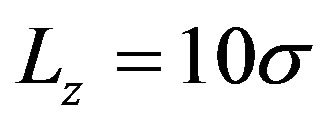 and
and 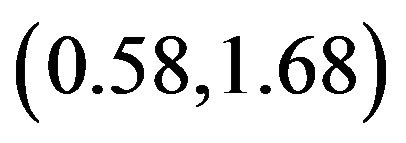 at
at  [34]. Consistent with this tendency, the TCP of the quasi-2D Stockmayer fluid (which corresponds to the limit
[34]. Consistent with this tendency, the TCP of the quasi-2D Stockmayer fluid (which corresponds to the limit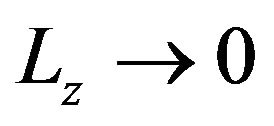 ) is found at even lower density and temperature, specifically at
) is found at even lower density and temperature, specifically at  and
and
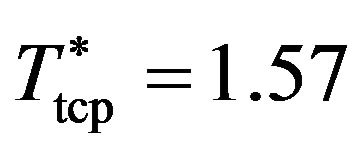 . A somewhat different behavior emerges in the chemical potential-temperature representation depicted in Figure 1(b). From the location of the TCPs, we see that the tricritical chemical potential,
. A somewhat different behavior emerges in the chemical potential-temperature representation depicted in Figure 1(b). From the location of the TCPs, we see that the tricritical chemical potential,  , of the quasi-2D fluid
, of the quasi-2D fluid 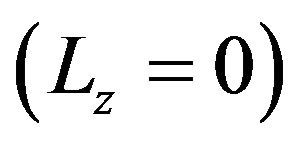 is only slightly smaller than that of its 3D counterpart
is only slightly smaller than that of its 3D counterpart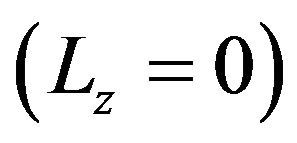 . On the other hand, the corresponding values for
. On the other hand, the corresponding values for  of confined Stockmayer fluids
of confined Stockmayer fluids  are significantly smaller (consistent with [35]). We attribute this non-monotonic behavior of
are significantly smaller (consistent with [35]). We attribute this non-monotonic behavior of 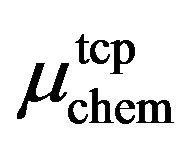 upon lowering of
upon lowering of  [see Figure 1(b)] to the fact that, for the confined Stockmayer fluids, the walls were considered to be attractive [34]. This feature is known to support capillary condensation (or, more generally, the formation of denser phases), accompanied by lowering of the critical value of
[see Figure 1(b)] to the fact that, for the confined Stockmayer fluids, the walls were considered to be attractive [34]. This feature is known to support capillary condensation (or, more generally, the formation of denser phases), accompanied by lowering of the critical value of . The particles in the quasi-2D system do not interact with any walls; thus, there is no capillary condensation phenomenon. As a result,
. The particles in the quasi-2D system do not interact with any walls; thus, there is no capillary condensation phenomenon. As a result,  for the quasi-2D system nearly agrees with the 3D value.
for the quasi-2D system nearly agrees with the 3D value.
The reduction of spatial dimension not only shifts the TCP, it also has a profound influence on the topology of the phase diagram. Indeed, while the 3D Stockmayer fluid with the same dipole moment 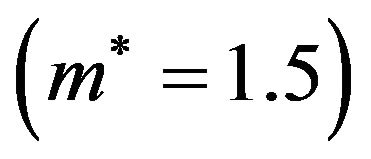 exhibits, in addition to the IF-FF transition, a condensation transition within the isotropic liquid (IL) phase, such a transition is absent in the quasi-2D system (see Figure 1). We can artificially stabilize a condensation transition in the 2D system by setting all order parameters (except from
exhibits, in addition to the IF-FF transition, a condensation transition within the isotropic liquid (IL) phase, such a transition is absent in the quasi-2D system (see Figure 1). We can artificially stabilize a condensation transition in the 2D system by setting all order parameters (except from ) to zero. The result of this calculation is indicated in Figure 1(a) by the red squares. It turns out that the IG-IL critical point
) to zero. The result of this calculation is indicated in Figure 1(a) by the red squares. It turns out that the IG-IL critical point  is located within the IF-FF phase coexistence region; therefore it is thermodynamically unstable. However, such IL configurations may still be relevant in the context of the phase separation kinetics (i.e., in non-equilibrium situations), where they can occur as transient states during the change from the IF to the FF state at a temperature
is located within the IF-FF phase coexistence region; therefore it is thermodynamically unstable. However, such IL configurations may still be relevant in the context of the phase separation kinetics (i.e., in non-equilibrium situations), where they can occur as transient states during the change from the IF to the FF state at a temperature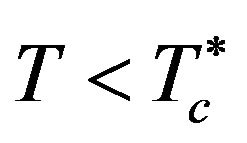 . We also note that the suppression of the IG-IL critical point is consistent with previous DFT results (at
. We also note that the suppression of the IG-IL critical point is consistent with previous DFT results (at ) in very narrow slitpores, such as
) in very narrow slitpores, such as  [34]. On the other hand, MC simulations for quasi-2D Stockmayer fluids predict stable isotropic liquid phases for dipole moments up to
[34]. On the other hand, MC simulations for quasi-2D Stockmayer fluids predict stable isotropic liquid phases for dipole moments up to
(at least) 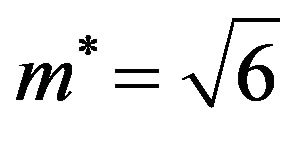 [13,14,17]. Therefore, the DFT seems to overestimate the stability of the ferroelectric phase, similar as it does in 3D [34]. Within the DFT, one would expect a recovery of the isotropic liquid state when the LJ attraction finally dominates then dipolar coupling, i.e., when
[13,14,17]. Therefore, the DFT seems to overestimate the stability of the ferroelectric phase, similar as it does in 3D [34]. Within the DFT, one would expect a recovery of the isotropic liquid state when the LJ attraction finally dominates then dipolar coupling, i.e., when 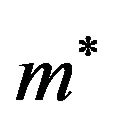 decreases towards even smaller values.
decreases towards even smaller values.
We now discuss in more detail the influence of spatial dimension and its interplay with the dipolar coupling strength on the tricritical point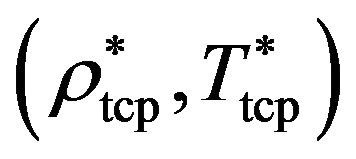 , above of which the low-temperature discontinuous transition between the IF and FF states changes into a (line of) second-order transition(s). Specifically, we are interested in the position of the TCPs, in the quasi-2D system and its 3D counterpart, as functions of the parameter
, above of which the low-temperature discontinuous transition between the IF and FF states changes into a (line of) second-order transition(s). Specifically, we are interested in the position of the TCPs, in the quasi-2D system and its 3D counterpart, as functions of the parameter . In previous DFT studies [30,31,34] it was already shown that the coupling strength influences the quantity
. In previous DFT studies [30,31,34] it was already shown that the coupling strength influences the quantity  much more than
much more than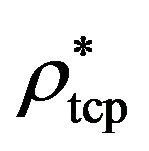 , at least as long as
, at least as long as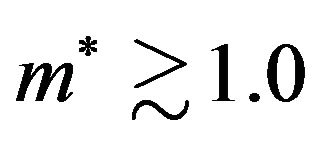 . Therefore, to estimate the dependence of
. Therefore, to estimate the dependence of  on
on  in the quasi-2D system, we set the density equal to tricritical density at
in the quasi-2D system, we set the density equal to tricritical density at , that is, to
, that is, to
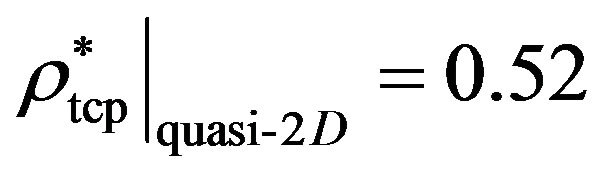 . The resulting function
. The resulting function 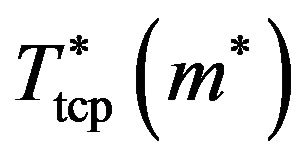 can then be easily determined from Equation (4). The same procedure is used for the 3D case, where the analog of Equation (3) reads [44]
can then be easily determined from Equation (4). The same procedure is used for the 3D case, where the analog of Equation (3) reads [44]
 (5)
(5)
with 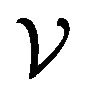 being the volume and
being the volume and 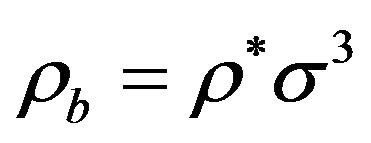 being the density of the bulk system. Equation (5) yields
being the density of the bulk system. Equation (5) yields
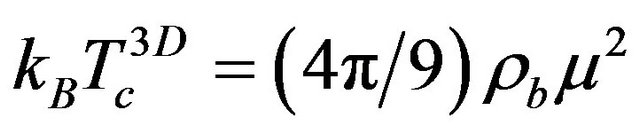 . Fixing the density to that of the tricritical point at
. Fixing the density to that of the tricritical point at  [34],
[34], 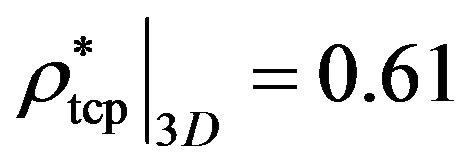 , we can again estimate the function
, we can again estimate the function  for a range of dipole moments. Numerical results for the quasi-2D system and its 3D analog are plotted in Figure 2.
for a range of dipole moments. Numerical results for the quasi-2D system and its 3D analog are plotted in Figure 2.
For both systems, the tricritical temperature increases with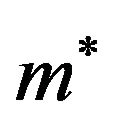 , as one may expect when the dipolar interactions (which stabilize the FF state) become more and more important as compared to the spherical attractive ones. More interestingly, Figure 2 reveals that reduction of spatial dimension shifts the tricritical temperatures towards lower values at fixed
, as one may expect when the dipolar interactions (which stabilize the FF state) become more and more important as compared to the spherical attractive ones. More interestingly, Figure 2 reveals that reduction of spatial dimension shifts the tricritical temperatures towards lower values at fixed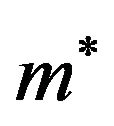 . This shift can be reasoned from Equations (3) and (5): in both the quasi- 2D and the 3D system, ordering competes with the same amount of (orientational) entropy, but the associated decrease of interaction energy
. This shift can be reasoned from Equations (3) and (5): in both the quasi- 2D and the 3D system, ordering competes with the same amount of (orientational) entropy, but the associated decrease of interaction energy  is less pronounced in the quasi-2D system. From a physical point of view, this diminishment is a consequence of the reduction of the number of neighbors in a 2D system relative to the bulk case. We also note another interesting point: whereas in the 3D system, only the long-range dipolar interactions contribute to the onset of ordering (see Equation (5)), the corresponding onset in the quasi- 2D system is also affected by the short-range interactions, as reflected by the appearance of the function
is less pronounced in the quasi-2D system. From a physical point of view, this diminishment is a consequence of the reduction of the number of neighbors in a 2D system relative to the bulk case. We also note another interesting point: whereas in the 3D system, only the long-range dipolar interactions contribute to the onset of ordering (see Equation (5)), the corresponding onset in the quasi- 2D system is also affected by the short-range interactions, as reflected by the appearance of the function 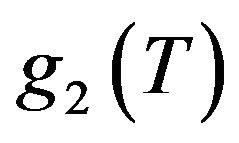 in Equation (3). Since the
in Equation (3). Since the 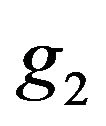 function increases upon cooling down, the curves
function increases upon cooling down, the curves 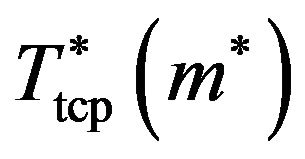 in Figure 2 for the quasi-2D and the 3D system, respectively, cross each other near
in Figure 2 for the quasi-2D and the 3D system, respectively, cross each other near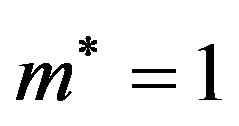 . However, since we assumed a constant tricritical density, the precise position of this crossing in Figure 2 should be considered with some caution.
. However, since we assumed a constant tricritical density, the precise position of this crossing in Figure 2 should be considered with some caution.
Finally, we briefly discuss the influence of the dimen-
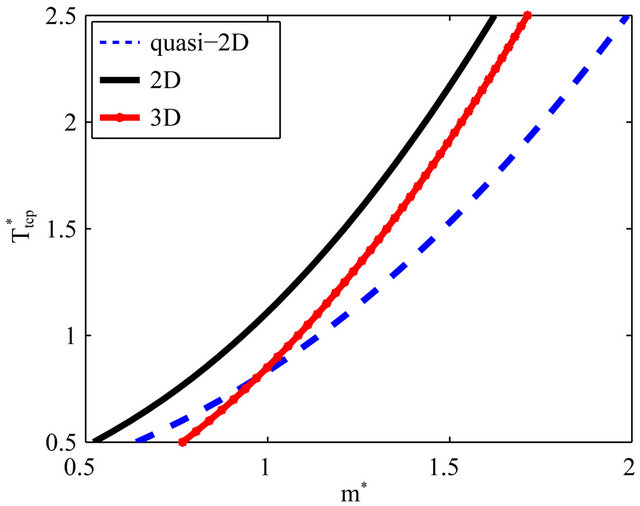
Figure 2. (Color online) Tricritical temperature  as function of the dipole moment
as function of the dipole moment 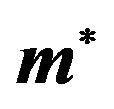 in the quasi-2D, 3D, and true 2D geometry. In all cases, the density has been set to that obtained at
in the quasi-2D, 3D, and true 2D geometry. In all cases, the density has been set to that obtained at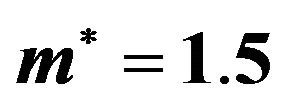 .
.
sion of the dipole vector (rather than that of the space accessible for the particles) on the appearance of ferroelectric order. Specifically, we consider a “true” 2D system where, in addition to the spatial confinement of the particles within the x-y-plane, the orientations of the dipole vectors are restricted to that plane as well. Indeed, as shown in previous simulations and theoretical studies (see, e.g., [15]) of 2D systems with freely rotating (i.e., three-dimensional) dipoles, these have a strong tendency to tilt into the confining plane especially at large coupling strengths. The “true” 2D system is therefore not completely unphysical. In the true 2D case, the orientational distribution function 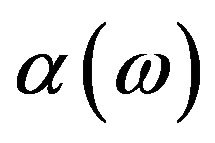 depends only on one angle,
depends only on one angle,  , which describes the orientation of
, which describes the orientation of  relative to, say, the x-axis. To obtain the grand canonical functional we expand
relative to, say, the x-axis. To obtain the grand canonical functional we expand 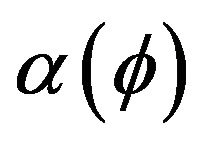 in a basis of exponential functions [16], i.e.,
in a basis of exponential functions [16], i.e.,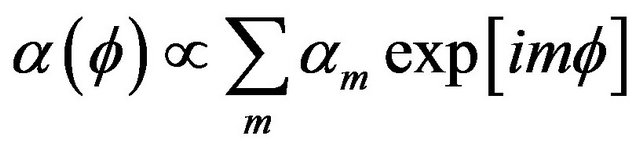 . Performing then the same Landau expansion as for the quasi-2D system, and isolating the terms proportional to the polarization, i.e. to
. Performing then the same Landau expansion as for the quasi-2D system, and isolating the terms proportional to the polarization, i.e. to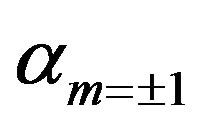 , the analog of Equation (3) reads
, the analog of Equation (3) reads
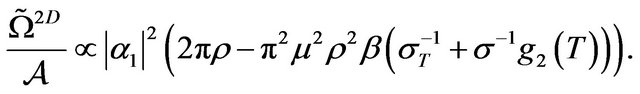 (6)
(6)
A direct comparison of Equation (6) with its quasi-2D analog in Equation (3) shows that, at fixed density, the ferroelectric ordering in the true 2D system occurs at a higher temperature. This is a consequence of the decrease of the dipolar fluctuations (and thus, the orientational entropy) due to their restriction to the plane. Moreover, as revealed in Figure 2 by the corresponding curve , the ordering is even promoted relative to the 3D case. This is consistent with tendencies found in a recent integral equation study [16], although the latter predicts, for the low-temperature behavior, large ferroelectric domains rather than true long-range ferroelectric order.
, the ordering is even promoted relative to the 3D case. This is consistent with tendencies found in a recent integral equation study [16], although the latter predicts, for the low-temperature behavior, large ferroelectric domains rather than true long-range ferroelectric order.
4. Summary and Conclusions
In this work we have calculated the fluid phase diagram of a quasi-2D Stockmayer fluid by means of density functional theory in the modified mean-field approximation. At the dipole moment considered 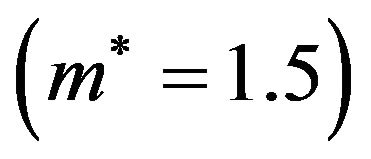 the system exhibits an isotropic fluid phase where the dipole moments are randomly oriented, yet with a preference for in-plane directions, and a ferroelectric fluid phase characterized by global, in-plane polarization. Apart from exploring the quasi-2D phase behavior, another focus of our study was to identify the role of the dimension of accessible space, as well as that of the dimension of the dipole vector. To quantify these effects on a mean-field level, we have considered the location of the tricritical point. Regarding the impact of space dimension, we have found that decreasing the system’s dimension in z-direction from the bulk limit
the system exhibits an isotropic fluid phase where the dipole moments are randomly oriented, yet with a preference for in-plane directions, and a ferroelectric fluid phase characterized by global, in-plane polarization. Apart from exploring the quasi-2D phase behavior, another focus of our study was to identify the role of the dimension of accessible space, as well as that of the dimension of the dipole vector. To quantify these effects on a mean-field level, we have considered the location of the tricritical point. Regarding the impact of space dimension, we have found that decreasing the system’s dimension in z-direction from the bulk limit 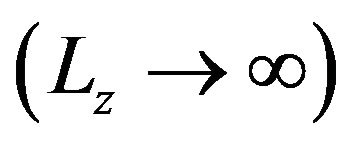 over slab systems
over slab systems 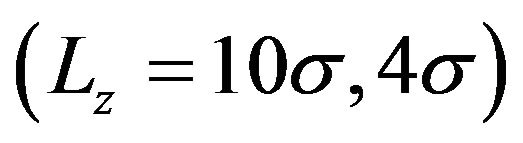 towards the 2D limit
towards the 2D limit 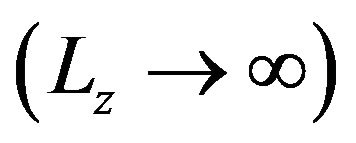 shifts the TCP towards lower temperatures and densities. Furthermore, the disappearance of the isotropic liquid phase in the quasi-2D system also shows that the confinement enhances the stability of dense ordered phases relative to disordered ones. Clearly, care has to be taken with respect to the predictions of our mean-field-like DFT approach on a quantitative level. Indeed, from computer simulations [13,14,17] it is known that a quasi-2D Stockmayer fluid at
shifts the TCP towards lower temperatures and densities. Furthermore, the disappearance of the isotropic liquid phase in the quasi-2D system also shows that the confinement enhances the stability of dense ordered phases relative to disordered ones. Clearly, care has to be taken with respect to the predictions of our mean-field-like DFT approach on a quantitative level. Indeed, from computer simulations [13,14,17] it is known that a quasi-2D Stockmayer fluid at 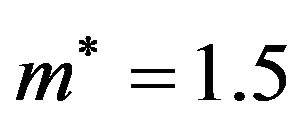 does have a stable isotropic liquid phase at densities beyond the isotropic vapor-liquid critical point, which is absent in our study. This discrepancy reflects the well-known tendency of the DFT to overestimate the stability of ordered phases. However, based on previous DFT studies for bulk and confined systems one would expect a recovery of the isotropic liquid state in the quasi-2D case upon further decrease of
does have a stable isotropic liquid phase at densities beyond the isotropic vapor-liquid critical point, which is absent in our study. This discrepancy reflects the well-known tendency of the DFT to overestimate the stability of ordered phases. However, based on previous DFT studies for bulk and confined systems one would expect a recovery of the isotropic liquid state in the quasi-2D case upon further decrease of . A further interesting result of our study concerns the role of the spin dimension. Here we have found that complete restriction of the dipole moments on in-plane directions yields ferroelectric ordering at temperatures not only higher than those in the quasi-2D system, but even higher than those in 3D.
. A further interesting result of our study concerns the role of the spin dimension. Here we have found that complete restriction of the dipole moments on in-plane directions yields ferroelectric ordering at temperatures not only higher than those in the quasi-2D system, but even higher than those in 3D.
There remains the question whether fluid states with long-range ferroelectric order, as predicted by DFT, exist at all in quasi-2D and true 2D systems. As mentioned in the introduction, computer simulations give conflicting answers, which may also depend on the number of particles considered in the simulation (indeed, the MD study on quasi-2D systems by Ouyang et al. [17], which does predict long-range ferroelectric ordering, involves a rather small system size). We should therefore interpret the present DFT results, which rely on the assumption of a spatially homogeneous orientational structure, such that the 2D geometry definitely promotes the existence of large ferroelectric domains, but not necessarily true longrange order.
Despite these pitfalls, the DFT approach provides a general overview of the phase diagrams and highlights the dimensionality effects by providing the leading order terms in the free energy. From that perspective, it would be interesting to extend the study towards 2D systems in external fields.
REFERENCES
- K. Butter, P. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, “Direct Observation of Dipolar Chains in Ferrofluids in Zero Field Using Cryogenic Electron Microscopy,” Journal of Physics: Condensed Matter, Vol. 15, No. 15, 2003, Article ID: S1451. doi:10.1088/0953-8984/15/15/310
- M. Klokkenburg, R. P. A. Dullens, W. K. Kegel, B. H. Erne and A. P. Philipse, “Quantitative Real-Space Analysis of Self-Assembled Structures of Magnetic Dipolar Colloids,” Physical Review Letters, Vol. 96, No. 3, 2006, Article ID: 037203. doi:10.1103/PhysRevLett.96.037203
- N. Osterman, D. Babic, I. Poberaj, J. Dobnikar and P. Ziherl, “Observation of Condensed Phases of Quasiplanar Core-Softened Colloids,” Physical Review Letters, Vol. 99, No. 24, 2007, Article ID: 248301. doi:10.1103/PhysRevLett.99.248301
- J. Richardi, M. P. Pileni and J. J. Weis, “Self-Organization of Magnetic Nanoparticles: A Monte Carlo Study,” Physical Review E, Vol. 77, No. 6, 2008, Article ID: 061510. doi:10.1103/PhysRevE.77.061510
- S. O. Lumsdon, E. W. Kaler and O. D. Velev, “Two-Dimensional Crystallization of Microspheres by a Coplanar AC Electric Field,” Langmuir, Vol. 20, No. 6, 2004, pp. 2108-2116. doi:10.1021/la035812y
- J. J. Jurez and M. A. Bevana, “Interactions and Microstructures in Electric Field Mediated Colloidal Assembly,” Journal of Chemical Physics, Vol. 131, No. 13, 2009, Article ID: 134704. doi:10.1063/1.3241081
- S. C. Glotzer and M. J. Solomon, “Anisotropy of Building Blocks and Their Assembly into Complex Structures,” Nature Materials, Vol. 6, 2007, pp. 557-562. doi:10.1038/nmat1949
- K. H. Bhatt and O. D. Velev, “Control and Modeling of the Dielectrophoretic Assembly of On-Chip Nanoparticle Wires,” Langmuir, Vol. 20, No. 2, 2004, Article ID: 467476. doi:10.1021/la0349976
- J. J. Weis, “Preliminary Communication Orientational Structure of Quasi-Two-Dimensional Dipolar Hard Spheres,” Molecular Physics: An International Journal at the Interface between Chemistry and Physics, Vol. 93, No. 3, 1998, pp. 361-364. doi:10.1080/002689798169023
- J. M. Tavares, J. J. Weis and M. M. Telo da Gama, “Quasi-Two-Dimensional Dipolar Fluid at Low Densities: Monte Carlo Simulations and Theory,” Physical Review E, Vol. 65, No. 6, 2002, Article ID: 061201. doi:10.1103/PhysRevE.65.061201
- J. M. Tavares, J. J. Weis and M. M. Telo da Gama, “Phase transition in Two-Dimensional Dipolar Fluids at Low Densities,” Physical Review E, Vol. 73, No. 4, 2006, Article ID: 041507. doi:10.1103/PhysRevE.73.041507
- P. D. Duncan and P. J. Camp, “Aggregation Kinetics and the Nature of Phase Separation in Two-Dimensional Dipolar Fluids,” Physical Review Letters, Vol. 121, No. 10, 2006, Article ID: 107202. doi:10.1103/PhysRevLett.97.107202
- G. T. Gao, X. C. Zeng and W. Wang, “Vapor-Liquid Coexistence of Quasi-Two-Dimensional Stockmayer Fluids,” Journal of Chemical Physics, Vol. 106, No. 8, 1997, Article ID: 3311. doi:10.1063/1.473079
- H. Schmidle and S. H. L. Klapp, “Phase Transitions of TwoDimensional Dipolar Fluids in External Fields,” Journal of Chemical Physics, Vol. 134, 2011, Article ID: 114903.
- E. Lomba, F. Lado and J. J. Weis, “Structure and Thermodynamics of a Ferrofluid Monolayer,” Physical Review E, Vol. 61, No. 4, 2000, pp. 3838-3849. doi:10.1103/PhysRevE.61.3838
- L. Luo and S. H. L. Klapp, “Fluctuations in a ferrofluid Monolayer: An Integral Equation Study,” Journal of Chemical Physics, Vol. 131, No. 3, 2009, Article ID: 034709. doi:10.1063/1.3176210
- W.-Z. Ouyang, S.-H. Xu and Z.-W. Sun, “Gas-Liquid Phase Coexistence in Quasi-Two-Dimensional Stockmayer Fluids: A Molecular Dynamics Study,” Journal of Chemical Physics, Vol. 134, No. 1, 2011, Article ID: 014901. doi:10.1063/1.3521393
- J.-J. Weis, “Orientational Structure in a Monolayer of Dipolar Hard Spheres,” Molecular Physics: An International Journal at the Interface between Chemistry and Physics, Vol. 100, No. 5, 2002, pp. 579-594. doi:10.1080/00268970110097136
- V. Russier, “Calculated Magnetic Properties of Two-Dimensional Arrays of Nanoparticles at vanishing Temperature,” Journal of Applied Physics, Vol. 89, No. 2, 2001, Article ID: 1287. doi:10.1063/1.1333034
- P. Politi, M. G. Pini and R. L. Stamps, “Dipolar Ground State of Planar Spins on Triangular Lattices,” Physical Review B, Vol. 73, No. 2, 2006, Article ID: 020405. doi:10.1103/PhysRevB.73.020405
- D. Wei and G. N. Patey, “Orientational Order in Simple Dipolar Liquids: Computer Simulation of a Ferroelectric Nematic Phase,” Physical Review Letters, Vol. 68, No. 13, 1992, pp. 2043-2045. doi:10.1103/PhysRevLett.68.2043
- D. Levesque, J.-J. Weis and G. J. Zarragoicoechea, “Orientational Order in Simple Dipolar Liquid-Crystal Models,” Physical Review Letters, Vol. 69, No. 6, 1992, pp. 913- 916. doi:10.1103/PhysRevLett.69.913
- J. J. Weis and D. Levesque, “Orientational Order in High Density Dipolar Hard Sphere Fluids,” Journal of Chemical Physics, Vol. 125, No. 3, 2006, Article ID: 034504. doi:10.1063/1.2215614
- S. H. L. Klapp and M. Schoen, “Spontaneous Orientational Order in Confined Dipolar Fluid Films,” Journal of Chemical Physics, Vol. 117, No. 17, 2002, Article ID: 8050. doi:10.1063/1.1512282
- R. A. Trasca and S. H. L. Klapp, “Structure Formation in Layered Ferrofluid Nanofilms,” Journal of Chemical Physics, Vol. 129, No. 8, 2008, Article ID: 084702. doi:10.1063/1.2971182
- P. I. Teixeira and M. M. Telo da Gama, “Density-Functional Theory for the Interfacial Properties of a Dipolar Fluid,” Journal of Physics: Condensed Matter, Vol. 3, No. 1, 1991, p. 111. doi:10.1088/0953-8984/3/1/009
- P. Frodl and S. Dietrich, “Bulk and Interfacial Properties of Polar and Molecular Fluids,” Physical Review A, Vol. 45, No. 10, 1992, pp. 7330-7354. doi:10.1103/PhysRevA.45.7330
- J. M. Tavares, M. M. Telo da Gama, P. I. C. Teixeira, J.-J. Weis and M. J. P. Nijmeijer, “Phase Diagram and Critical Behavior of the Ferromagnetic Heisenberg Fluid from Density-Functional Theory,” Physical Review E, Vol. 52, No. 2, 1995, pp. 1915-1929. doi:10.1103/PhysRevE.52.1915
- G. M. Range and S. H. L. Klapp, “Density Functional Study of the Phase Behavior of Asymmetric Binary Dipolar Mixtures,” Physical Review E, Vol. 69, No, 4, 2004, Article ID: 041201. doi:10.1103/PhysRevE.69.041201
- B. Groh and S. Dietrich, “Long-Ranged Orientational Order in Dipolar Fluids,” Physical Review Letters, Vol. 72, No. 15, 1994, pp. 2422-2425. doi:10.1103/PhysRevLett.72.2422
- B. Groh and S. Dietrich, “Ferroelectric Phase in Stockmayer Fluids,” Physical Review E, Vol. 50, No. 5, 1994, pp. 3814-3833. doi:10.1103/PhysRevE.50.3814
- B. Groh and S. Dietrich, “Structural and Thermal Properties of Orientationally Ordered Dipolar Fluids,” Physical Review E, Vol. 53, No. 3, 1996, pp. 2509-2530. doi:10.1103/PhysRevE.53.2509
- B. Groh and S. Dietrich, “Spatial Structures of Dipolar Ferromagnetic Liquids,” Physical Review Letters, Vol. 79, No. 4, 1997, pp. 749-752. doi:10.1103/PhysRevLett.79.749
- M. Gramzow and S. H. L. Klapp, “Capillary Condensation and Orientational Ordering of Confined Polar Fluids,” Physical Review E, Vol. 75, No. 1, 2007, Article ID: 011605. doi:10.1103/PhysRevE.75.011605
- I. Szalai and S. Dietrich, “Phase Transitions and Ordering of Confined Dipolar Fluids,” The European Physical Journal E, Vol. 28, No. 3, 2009, pp. 347-359. doi:10.1140/epje/i2008-10424-2
- J. A. Barker and D. Henderson, “Perturbation Theory and Equation of State for Fluids. II. A Successful Theory of Liquids,” Journal of Chemical Physics, Vol. 47, No. 11, 1967, Article ID: 4714. doi:10.1063/1.1701689
- J. P. Hansen and I. R. McDonald, “Theory of Simple Liquids,” 3rd Edition, Academic Press, Amsterdam, 2006.
- R. Geiger, “Long-Range Order in Quasi-Two-Dimensional Dipolar Fluids: A Density Functional Study,” Master Thesis, Technische Universität, Berlin, 2008. https://sites.google.com/site/researchgeiger/
- P. Nielaba and S. Sengupta, “Perturbative Density FunctioNal Theory for Phase Transitions in a Two-Dimensional Antiferromagnetic Fluid,” Physical Review E, Vol. 55, No. 3, 1997, pp. 3754-3757. doi:10.1103/PhysRevE.55.3754
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. F. Flannery, “Numerical Recipes 3rd Edition: The Art of Scientific Computing,” Cambridge University Press, Cambridge, 2007.
- M. E. van Leeuwen, “Derivation of Stockmayer Potential Parameters for Polar Fluids,” Fluid Phase Equilibria, Vol. 99, 1994, pp. 1-18. doi:10.1016/0378-3812(94)80018-9
- A. Schreiber, H. Bock, M. Schoen and G. Findenegg, “Effect of Surface Modification on the Pore Condensation of Fluids: Experimental Results and Density Functional Theory,” Molecular Physics, Vol. 100, No. 13, 2002, pp. 2097-2107. doi:10.1080/00268970210132559
- E. Lomba, J. J. Weis, N. G. Almarza, F. Bresme and G. Stell, “Phase Transitions in a Continuum Model of the Classical Heisenberg Magnet: The Ferromagnetic System,” Physical Review E, Vol. 49, No. 6, 1994, pp. 5169-5178. doi:10.1103/PhysRevE.49.5169
- To obtain Equation (5) we have taken the limit
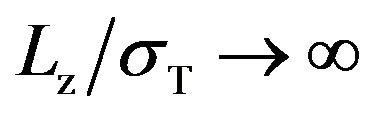 of the corresponding equation for slab-like systems (see Equation (2.53) in ).
of the corresponding equation for slab-like systems (see Equation (2.53) in ).

