Journal of Modern Physics
Vol.3 No.11(2012), Article ID:24389,7 pages DOI:10.4236/jmp.2012.311210
Ab Initio Calculation of 2H and 4He Binding Energies
7, rue de l’Ambroisie 75012 Paris, France
Email: bschaeffer@wanadoo.fr
Received August 20, 2012; revised September 20, 2012; accepted October 2, 2012
Keywords: Electromagnetic Moments; Nuclear Forces; Binding Energy Nucleon; Nucleon Interaction; Deuteron; Alpha Particle
ABSTRACT
The binding energies of all hydrogen isotopes have been calculated successfully for the first time in a previous paper [J Fusion Energy, 30 (2011) 377], using only the electric and magnetic Coulomb’s laws, without using the hypothetical shell model of the nucleus and its mysterious strong force. In this paper, an elementary calculation gives the order of magnitude of the nuclear interaction. The binding energies of the deuteron and the alpha particle are then calculated by taking into account the proton induced electric dipole in the neutron. The large binding energy per nucleon of 4He, as compared to that of 2H, has been explained by a larger electric attraction combined with a lower magnetic repulsion. The binding energies have been calculated without fitting, using only fundamental laws and constants, proving that the nuclear interaction is only electromagnetic.
1. Introduction
It is known since one century that radium releases a huge energy, one million times larger than any combustion energy, according to Pierre Curie. Let us compare the separation energy ratio of a proton from a neutron over that of an electron from a proton. The measured value of this ratio is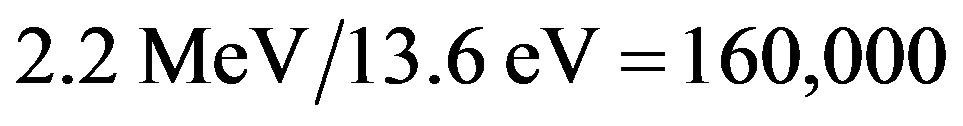 , less than the million expected because the deuteron is lightly bound. The radius ratio of the hydrogen atom
, less than the million expected because the deuteron is lightly bound. The radius ratio of the hydrogen atom 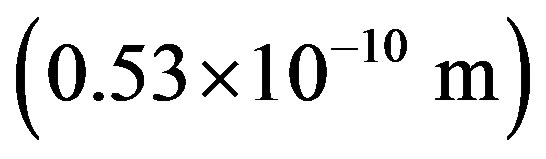 over the proton’s
over the proton’s  is above 50,000. As far as I know, no theoretical formula for the proton radius exists. A simple approach using the proton Compton radius
is above 50,000. As far as I know, no theoretical formula for the proton radius exists. A simple approach using the proton Compton radius 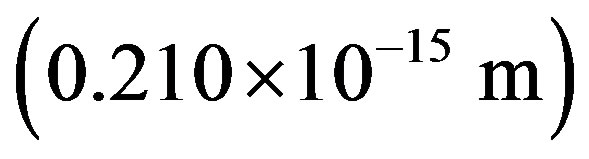 as the proton radius, leads to a formula giving an order of magnitude of the nuclear binding energy,
as the proton radius, leads to a formula giving an order of magnitude of the nuclear binding energy, 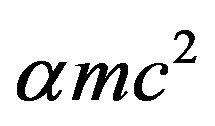 , predicting the nuclear energy to be around
, predicting the nuclear energy to be around 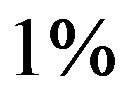 of the mass energy. Therefore, the nuclear to chemical energy ratio is shown to be 250,000, not far from the experimental value 160,000 of the ratio between the binding energies of the deuteron and the hydrogen atom. More precise calculations using the electromagnetic neutron-proton interaction confirm this rough approximation as it will be shown below.
of the mass energy. Therefore, the nuclear to chemical energy ratio is shown to be 250,000, not far from the experimental value 160,000 of the ratio between the binding energies of the deuteron and the hydrogen atom. More precise calculations using the electromagnetic neutron-proton interaction confirm this rough approximation as it will be shown below.
2. Simple Approach to the Nuclear Interaction
The Bohr radius of the hydrogen atom (Figure 1) is:
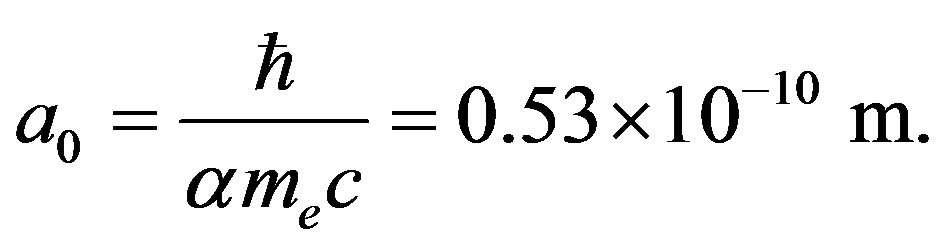 (1)
(1)
where
 (2)
(2)
is the fine structure constant,  , Planck’s constant,
, Planck’s constant, 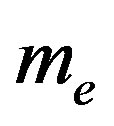 , the electron mass and
, the electron mass and , the light velocity. No theoretical formula existing for the radius of a nucleon [1], we shall use the proton Compton radius
, the light velocity. No theoretical formula existing for the radius of a nucleon [1], we shall use the proton Compton radius 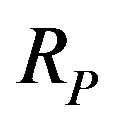 instead although it is four times smaller than the experimentally evaluated value of the proton radius:
instead although it is four times smaller than the experimentally evaluated value of the proton radius:
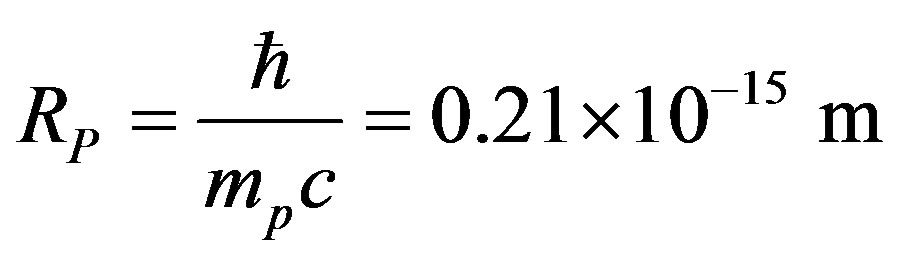 (3)
(3)
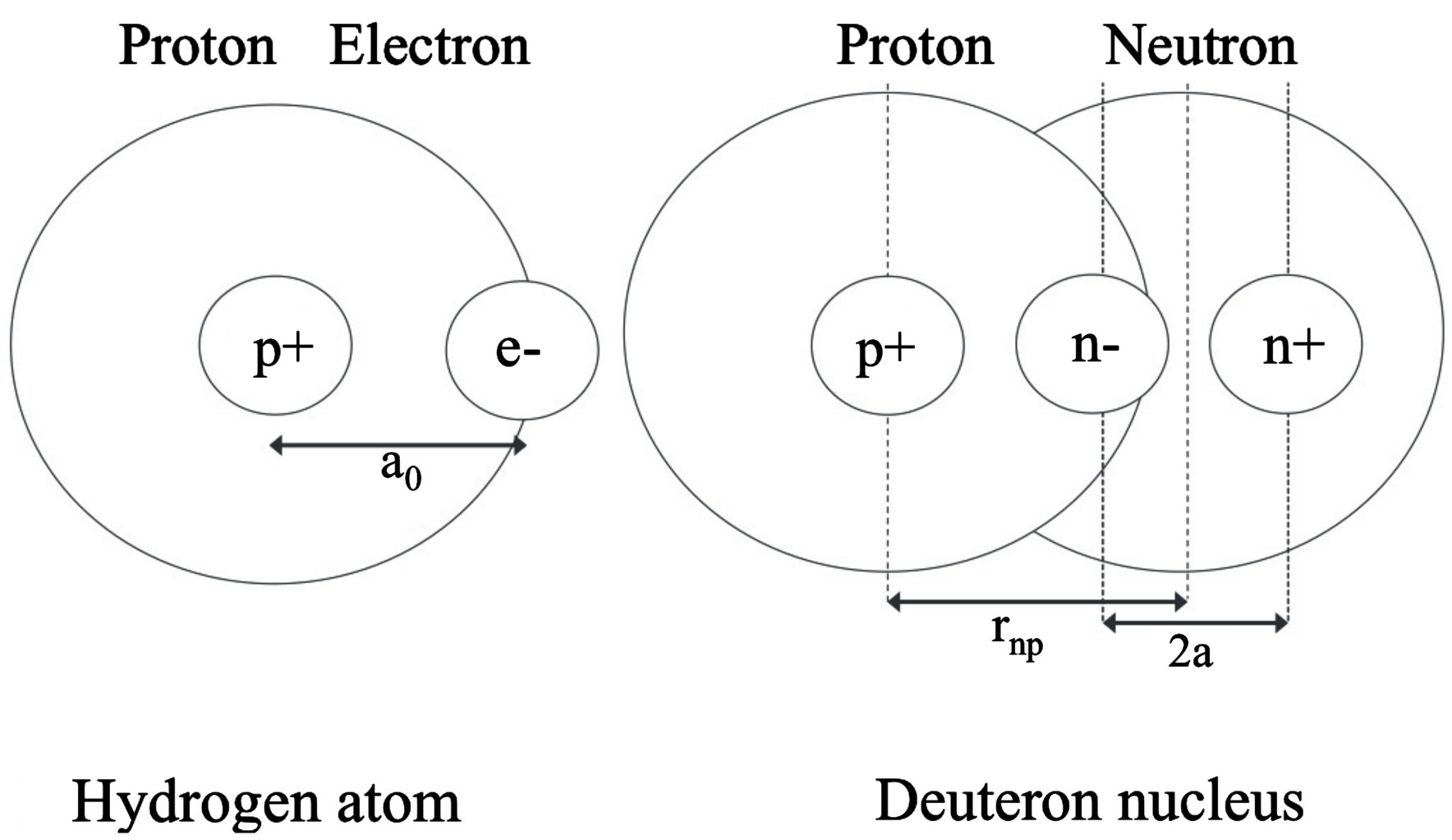
Figure 1. Comparison between the electron and neutron distances from a proton. 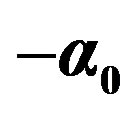 is the Bohr radius,
is the Bohr radius,  is the proton-neutron separation distance and 2a the separation distance between the electric charges of the neutron’s electric dipole induced by the proton.
is the proton-neutron separation distance and 2a the separation distance between the electric charges of the neutron’s electric dipole induced by the proton.
The ratio of the Bohr radius 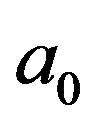 (1) over the proton Compton radius
(1) over the proton Compton radius 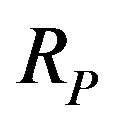 (3) is:
(3) is:
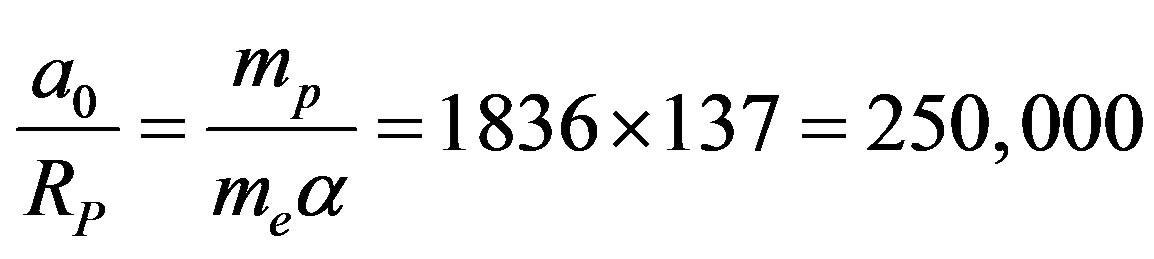 (4)
(4)
where 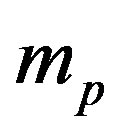 is the proton mass. The Bohr formula of the binding energy of the fundamental state of the hydrogen atom is:
is the proton mass. The Bohr formula of the binding energy of the fundamental state of the hydrogen atom is:
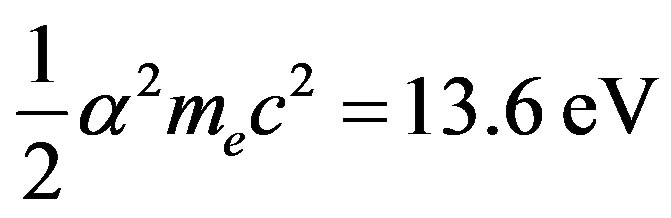 (5)
(5)
Newton’s law of gravitation and Coulomb’s law of electricity are the only forces of nature having a potential energy inversely proportional to the distance. Assuming that it is the same for the nuclear interaction, the ratio 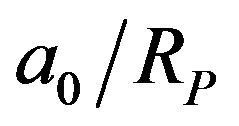 from Equation (4) is the ratio of nuclear and chemical energies. Multiplying it by the hydrogen atom binding energy (5) we obtain the total binding energy of the deuteron:
from Equation (4) is the ratio of nuclear and chemical energies. Multiplying it by the hydrogen atom binding energy (5) we obtain the total binding energy of the deuteron:
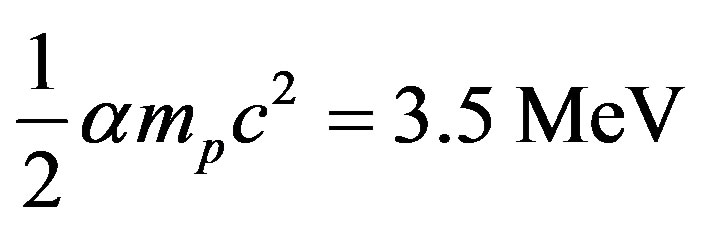 (6)
(6)
This value is larger than the experimental binding energy of the deuteron,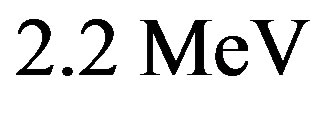 . The binding energies per nucleon varying from
. The binding energies per nucleon varying from 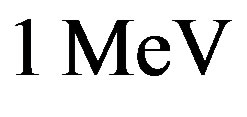 for the deuteron to
for the deuteron to 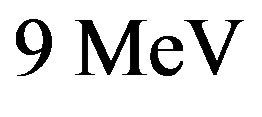 for iron, we may say that the order of magnitude of the nuclear binding energy per nucleon is around
for iron, we may say that the order of magnitude of the nuclear binding energy per nucleon is around
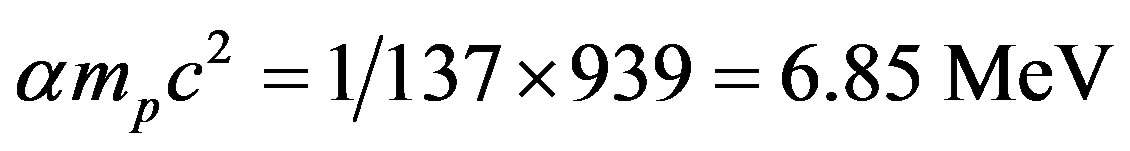 (7)
(7)
This value is, coincidentally, almost that of ,
,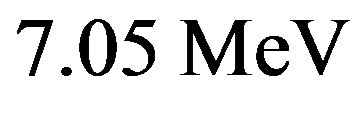 . This simple calculation based on the hypothesis of an inverse distance law for the nuclear potential predicts, as it is well known, the nuclear energy to be
. This simple calculation based on the hypothesis of an inverse distance law for the nuclear potential predicts, as it is well known, the nuclear energy to be
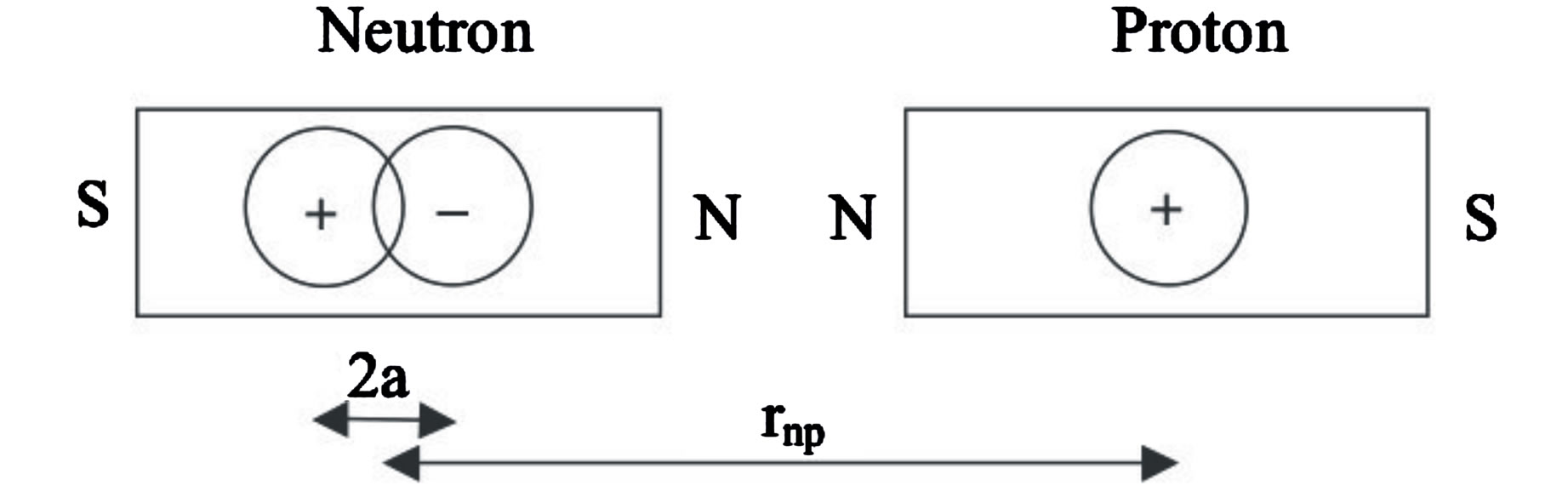
Figure 2. Schematic deuteron structure.  is the neutron-proton separation distance. 2a is the electric dipole moment separation distance. The electric and magnetic dipoles are at the centers of the nucleons. At large internucleon distances the electric neutron-proton interaction energy potential is that of a dipole, in
is the neutron-proton separation distance. 2a is the electric dipole moment separation distance. The electric and magnetic dipoles are at the centers of the nucleons. At large internucleon distances the electric neutron-proton interaction energy potential is that of a dipole, in , explaining the apparent neutrality of the neutron at large distances from a proton. At a short internucleon distance, the positive charge of the neutron is repulsed by the proton and its negative charge is attracted by the potential in
, explaining the apparent neutrality of the neutron at large distances from a proton. At a short internucleon distance, the positive charge of the neutron is repulsed by the proton and its negative charge is attracted by the potential in 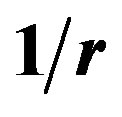 as in any electrostatic induction [2]. The magnetic moments of the neutron and the proton are opposite North-North (or SouthSouth) and collinear (not antiparallel as usually assumed), thus producing a repulsive interaction potential in
as in any electrostatic induction [2]. The magnetic moments of the neutron and the proton are opposite North-North (or SouthSouth) and collinear (not antiparallel as usually assumed), thus producing a repulsive interaction potential in 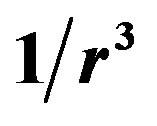 equilibrating the electrostatic attractive potential in
equilibrating the electrostatic attractive potential in .
.
around 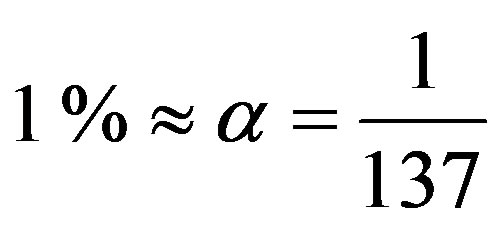 of the mass energy.
of the mass energy.
3. Electromagnetic Interaction in a Nucleus
In contrast with the Bohr planetary model of the atom, the nucleus has no nucleus and thus no fixed axis of rotation, the center of mass of the nucleus being not precisely defined. It is usually admitted that the centrifugal force is equilibrated by the mysterious strong force. It is assumed here that a static equilibrium between attractive electrostatic and repulsive magnetic forces exists.
The usual dipole and polarizability formulas being invalid in a non-uniform electric field e.g. between a neutron and a nearby proton, the original Coulomb’s law for point charges is used. The electrostatic interaction in the nucleus is due to the opposite elementary electric charges separated in a neutron by a nearby proton, inducing an electric dipole. The magnetic interaction between the proton and the neutron is due, in the deuteron, to the collinear and opposite magnetic moments of the nucleons (Figure 2).
In the  nucleus (Figure 3), the electromagnetic interaction works with the same principle as for
nucleus (Figure 3), the electromagnetic interaction works with the same principle as for  with two differences. First, the electrical dipole in a neutron is induced by two protons, implying a larger elec-
with two differences. First, the electrical dipole in a neutron is induced by two protons, implying a larger elec-

Figure 3. Tetrahedral alpha particle. The proton contains one elementary charge and the neutron two equal and opposite charges. All electric charges are assumed to be equal, in absolute value, to the elementary charge e. All magnetic moments are horizontal and perpendicular to the symmetry axis. The magnetic moments of the protons being opposite and collinear, the resulting magnetic moment is zero. Same thing for the neutrons. The magnetic moments of the protons are perpendicular to those of the neutrons. The tetrahedron is assumed to be regular: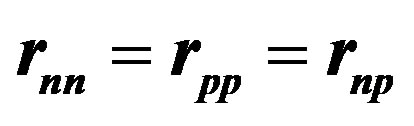 .
.
trical interaction energy than in . Second, the magnetic dipoles are inclined at
. Second, the magnetic dipoles are inclined at  with respect to the vertices, implying a lower neutron-proton repulsion. This explains the high binding energy of the
with respect to the vertices, implying a lower neutron-proton repulsion. This explains the high binding energy of the 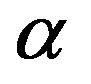 particle. Only universal and fundamental constants are used: elementary electrical charge
particle. Only universal and fundamental constants are used: elementary electrical charge , neutron and proton magnetic moments
, neutron and proton magnetic moments ,
,  , vacuum electric permittivity
, vacuum electric permittivity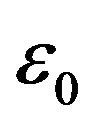 , magnetic permeability
, magnetic permeability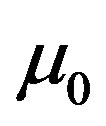 , light speed c or, equivalently, fine structure constant
, light speed c or, equivalently, fine structure constant , proton mass
, proton mass , neutron and proton Landé factors
, neutron and proton Landé factors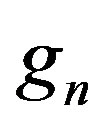 ,
, 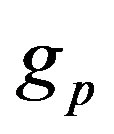 , proton Compton radius
, proton Compton radius .
.
3.1. Electric Charges in the Neutron
If the neutron had no charge, its electrostatic energy would be zero and it should be lighter than the proton. This is wrong: the neutron is heavier than the proton [2] by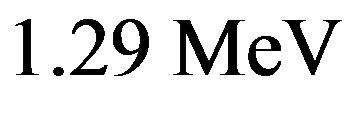 . The mass of the electron is
. The mass of the electron is 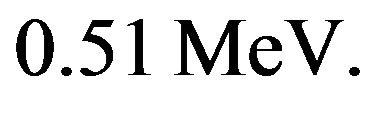 The kinetic energy of the electron, the proton and the electron antineutrino is the Q-value, difference between the masses before and after the free neutron
The kinetic energy of the electron, the proton and the electron antineutrino is the Q-value, difference between the masses before and after the free neutron  decay:
decay:
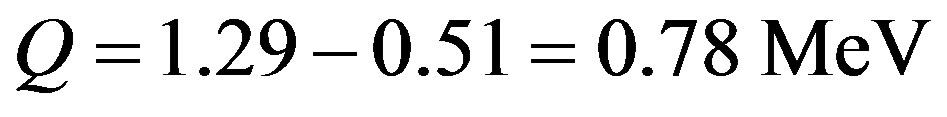 (8)
(8)
Gamow [3] suggested the electron-proton model where the neutron contains two opposite elementary electric point charges  and
and  and the proton only one positive point charge. The presence of electric charges in the neutron is known since the discovery of its magnetic moment [4].
and the proton only one positive point charge. The presence of electric charges in the neutron is known since the discovery of its magnetic moment [4].
3.2. Electric Dipoles
When a proton approaches a neutron, the positive electric charge of the neutron is repulsed by the proton while the negative charge is attracted, creating a dipole. This dipole is not permanent, it disappears when the proton goes far away from the neutron.
Let us see first the potential energy of a permanent dipole (only three collinear charges are considered here, 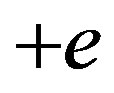 for the proton,
for the proton, 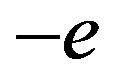 and
and 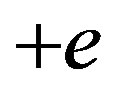 for the neutron):
for the neutron):
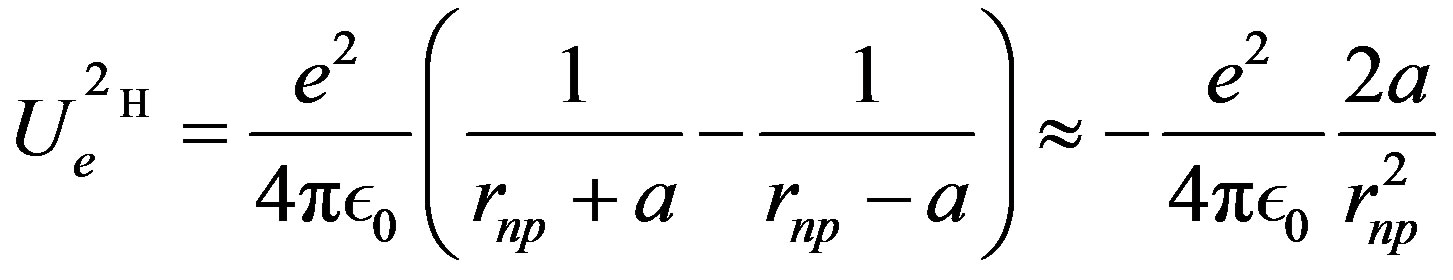 (9)
(9)
 is the distance between the proton and the dipole center.
is the distance between the proton and the dipole center. 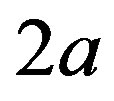 is the separation distance between the induced charges. The approximate dipole formula, at the right, is valid only when
is the separation distance between the induced charges. The approximate dipole formula, at the right, is valid only when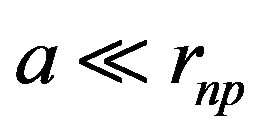 , in a quasi-uniform electric field. It will not be used here, where the separation distance between the neutron and the proton is comparable to the separation distance between the electric charges of the neutron. When the proton is bound to the neutron, the proton induced electric dipole, combined with the proton electric charge, becomes the quadrupole moment of the deuteron, Q = 0.288 fm
, in a quasi-uniform electric field. It will not be used here, where the separation distance between the neutron and the proton is comparable to the separation distance between the electric charges of the neutron. When the proton is bound to the neutron, the proton induced electric dipole, combined with the proton electric charge, becomes the quadrupole moment of the deuteron, Q = 0.288 fm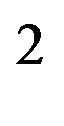 = (0.54 fm)
= (0.54 fm)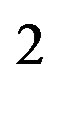 meaning that the distance between the electric charges is comparable to the nucleon size. The neutron dipole is not permanent: it is induced by the proton providing the energy needed to create the dipole. Therefore, the energy provided by the proton when it approaches the neutron has to be added to the self-energy of the dipole. Both energies being given by the same formula, the total interaction energy of the neutron and the proton is twice that of a permanent dipole:
meaning that the distance between the electric charges is comparable to the nucleon size. The neutron dipole is not permanent: it is induced by the proton providing the energy needed to create the dipole. Therefore, the energy provided by the proton when it approaches the neutron has to be added to the self-energy of the dipole. Both energies being given by the same formula, the total interaction energy of the neutron and the proton is twice that of a permanent dipole:
 (10)
(10)
An almost equivalent assumption is to assume that the neutron behaves like an isolated neutral conductor and that the proton is a point charge near to the neutron:
“When you bring a positive charge up to a conducting sphere, the positive charge attracts negative charges to the side closer to itself and leaves positive charges on the surface of the far side” [2].
This phenomenon, investigated by Faraday who called it “Electrification by Induction” [5], should also happen in the “not so neutral neutron” [6] even if its conductivity and charges are unknown. We have partial induction but we may consider it, in a first approximation, as a total induction. The charges induced by  (the proton) will thus be the same elementary charges
(the proton) will thus be the same elementary charges 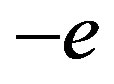 and
and  as above.
as above.
Formula (10) may be written differently (conversion formulas between (10) and (11) are given in the appendix):
 (11)
(11)
3.3. Magnetic Dipoles
In the deuteron , the neutron and the proton have opposite and, by reason of symmetry, collinear magnetic moments, resulting in a repulsive force. The magnetic moment of
, the neutron and the proton have opposite and, by reason of symmetry, collinear magnetic moments, resulting in a repulsive force. The magnetic moment of  being zero, the protons (same thing for the neutrons) are paired, collinear and opposite. Assuming provisionally a regular tetrahedron, the magnetic moments of the protons and the neutrons are, also by reason of symmetry, perpendicular and inclined at
being zero, the protons (same thing for the neutrons) are paired, collinear and opposite. Assuming provisionally a regular tetrahedron, the magnetic moments of the protons and the neutrons are, also by reason of symmetry, perpendicular and inclined at  with respect to the vertices of the assumed regular tetrahedron (Figure 3):
with respect to the vertices of the assumed regular tetrahedron (Figure 3):
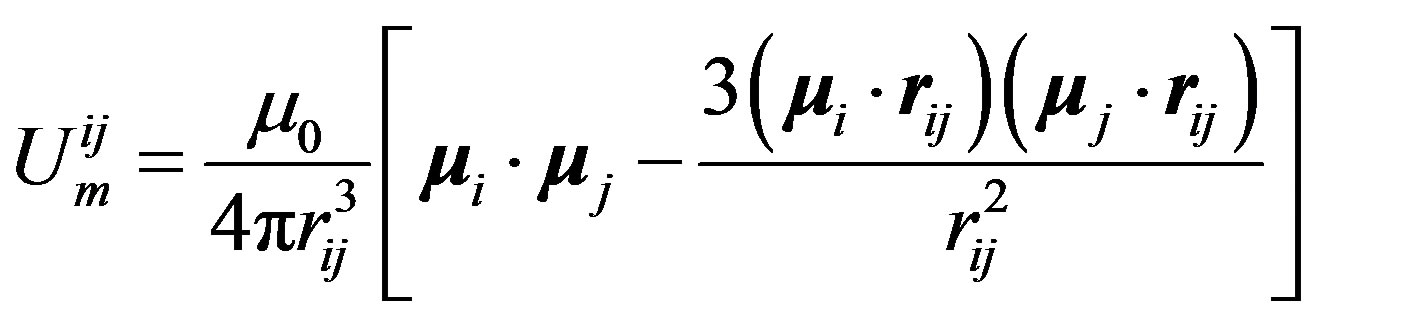 (12)
(12)
4. The Coulomb’s Laws
The electric Coulomb’s potential energy:
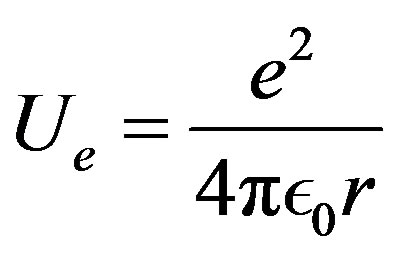 (13)
(13)
may be written equivalently for nuclear physics (see Appendix):
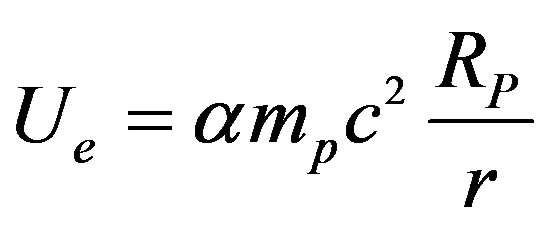 (14)
(14)
where  is the fine structure constant,
is the fine structure constant, 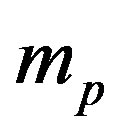 the proton mass,
the proton mass,  the light velocity and
the light velocity and 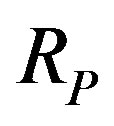 the proton Compton radius. A similar expression exists for the magnetic Coulomb’s potential as we shall see below.
the proton Compton radius. A similar expression exists for the magnetic Coulomb’s potential as we shall see below.
4.1. The Electromagnetic Potential Energy in a Nucleus
The sum of the electrostatic interaction energy potential between electric charges 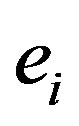 and
and 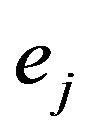 separated by
separated by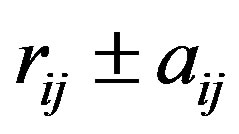 , plus the magnetic interaction energy potential between nucleons with magnetic moments
, plus the magnetic interaction energy potential between nucleons with magnetic moments 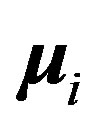 and
and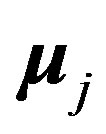 , separated by
, separated by 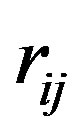 is [5,7,8]:
is [5,7,8]:
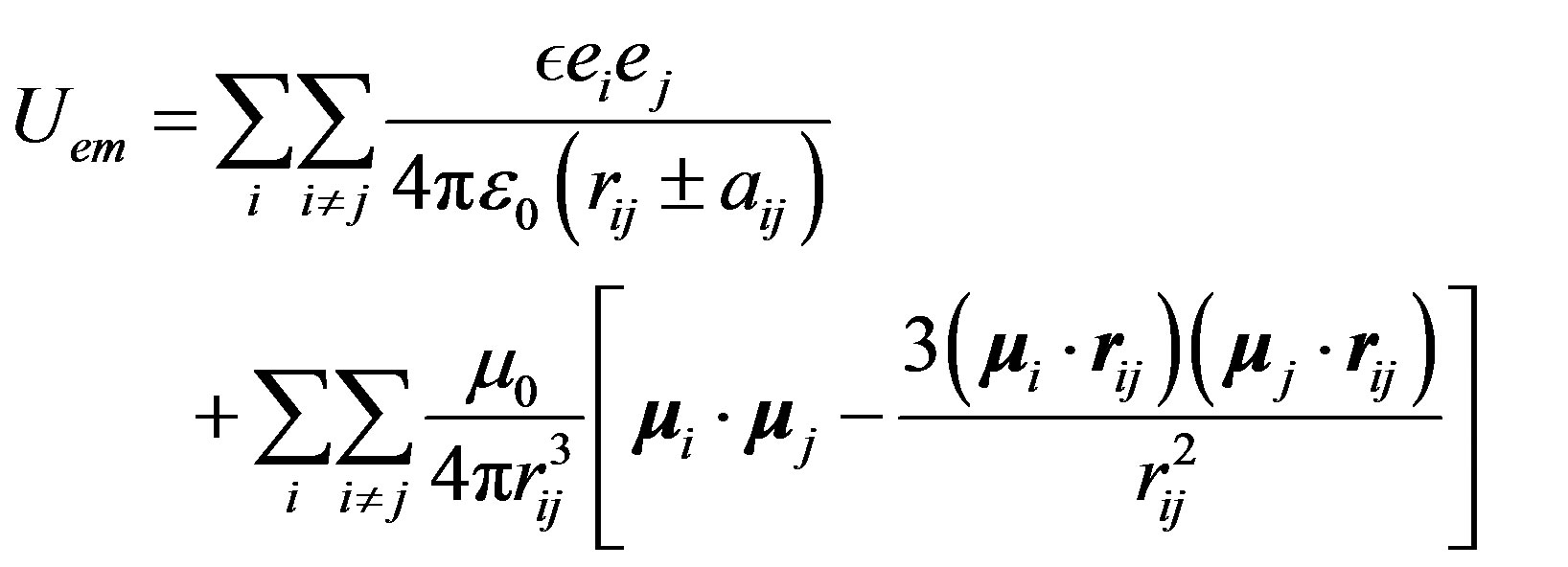 (15)
(15)
where  is the separation distance between the electric charges (always equal to e in absolute value in this paper) and
is the separation distance between the electric charges (always equal to e in absolute value in this paper) and 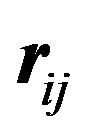 the separation vector between the nucleons magnetic moments. We have
the separation vector between the nucleons magnetic moments. We have  if the interaction is between a neutron and a proton because of the induced dipole, needing twice the energy of a permanent dipole; otherwise it is 1 between protons or 0 between neutrons. This general Formula (15) shows that the electric Coulomb potential is attractive or repulsive depending on the sign of the product of the interacting electric charges. The magnetic potential energy is attractive or repulsive depending on the relative orientation and position of the magnetic moments of the nucleons. Using the fundamental constants shown in the appendix, the general potential energy Formula (15) may be converted into:
if the interaction is between a neutron and a proton because of the induced dipole, needing twice the energy of a permanent dipole; otherwise it is 1 between protons or 0 between neutrons. This general Formula (15) shows that the electric Coulomb potential is attractive or repulsive depending on the sign of the product of the interacting electric charges. The magnetic potential energy is attractive or repulsive depending on the relative orientation and position of the magnetic moments of the nucleons. Using the fundamental constants shown in the appendix, the general potential energy Formula (15) may be converted into:
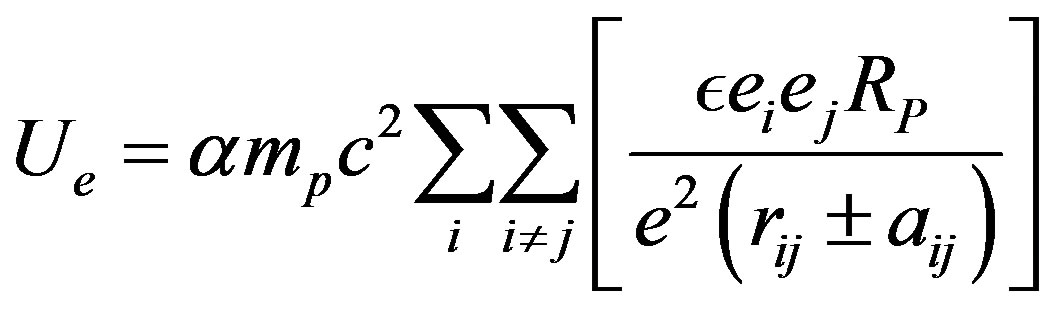 (16)
(16)
for the electrostatic potential and
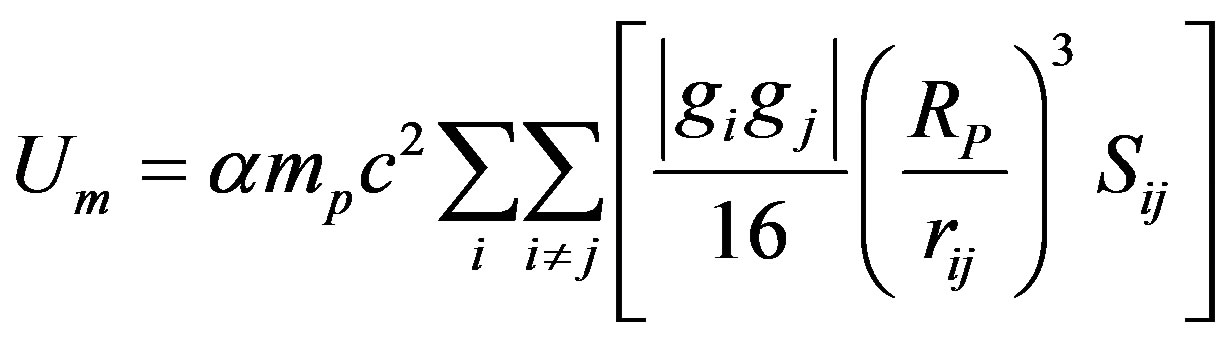 (17)
(17)
for the magnetic potential where the g’s are the Landé factors.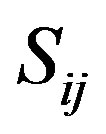 , positive for a magnetic repulsion and negative for a magnetic attraction, is the tensor operator [9],
, positive for a magnetic repulsion and negative for a magnetic attraction, is the tensor operator [9], 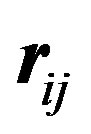 is the internucleon vector and
is the internucleon vector and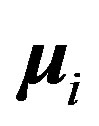 ,
, 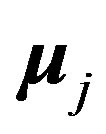 are the interacting magnetic moments of the nucleons
are the interacting magnetic moments of the nucleons 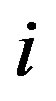 and
and :
:
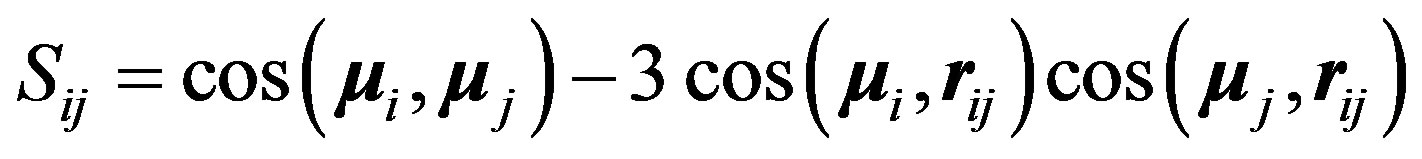 (18)
(18)
The electromagnetic nuclear potential is the product of 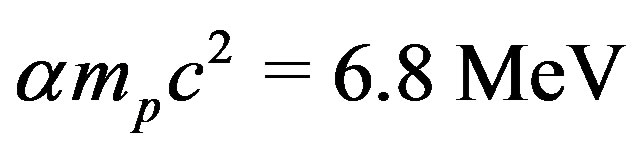 and a purely numerical function to be determined. The total electromagnetic potential is:
and a purely numerical function to be determined. The total electromagnetic potential is:
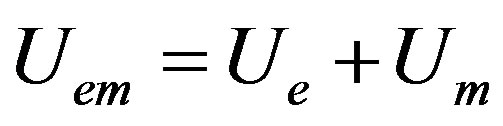 (19)
(19)
4.2. Deuteron Electromagnetic Energy Potential
The deuteron has one proton (one positive charge) and one neutron (two equal and opposite charges) (Figure 2) with three electric interactions and one magnetic interaction between the proton and the neutron. The proton interacts with the induced  and
and  charges of the neutron dipole. As seen above, the energy of the neutron electric dipole has to be added because it is not preexistent, thus multiplying by 2 the proton-neutron electrostatic interaction. Indeed the exact formula of the dipole potential is the same as for the interaction between a point charge and two opposite charges. The tensor operator is, for collinear and opposite magnetic moments, according to Formula (18):
charges of the neutron dipole. As seen above, the energy of the neutron electric dipole has to be added because it is not preexistent, thus multiplying by 2 the proton-neutron electrostatic interaction. Indeed the exact formula of the dipole potential is the same as for the interaction between a point charge and two opposite charges. The tensor operator is, for collinear and opposite magnetic moments, according to Formula (18):
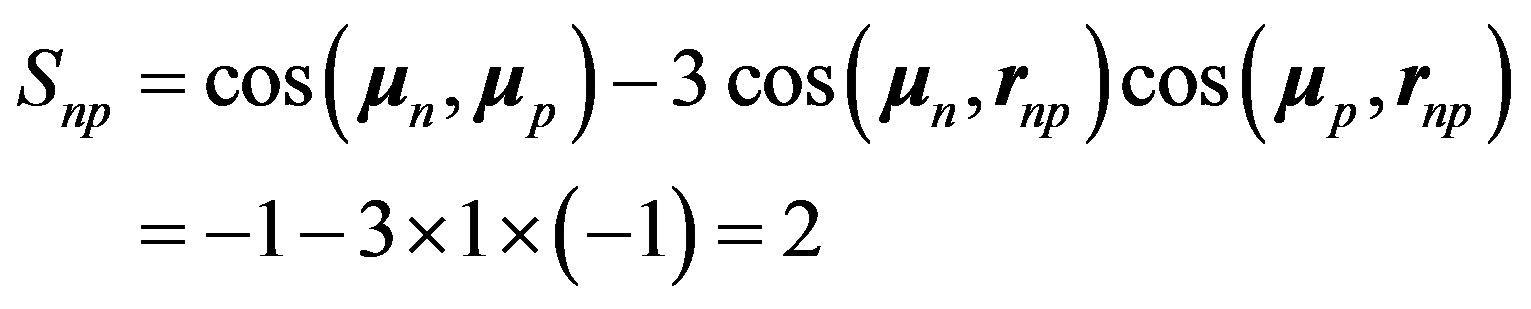 (20)
(20)
Formula (19) becomes:
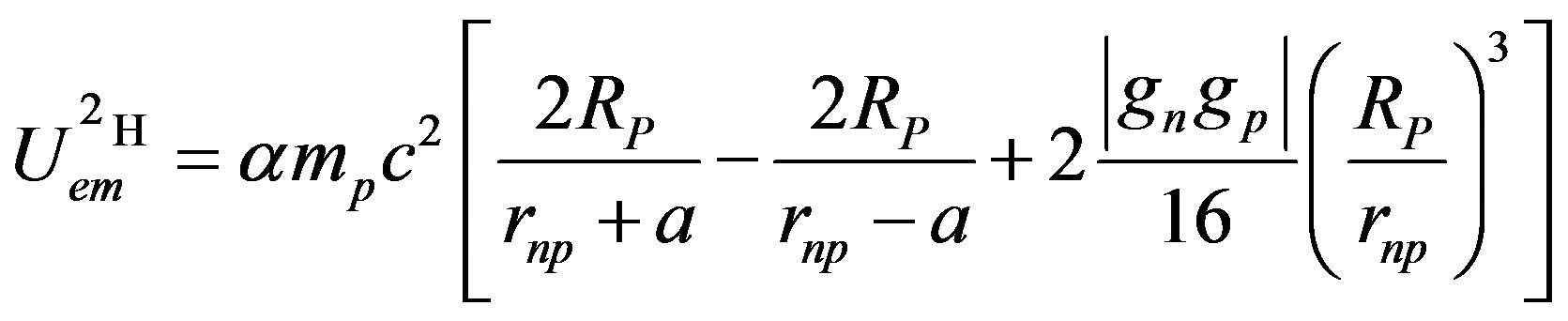 (21)
(21)
Numerically, in MeV, where the neutron-proton separation distance vector 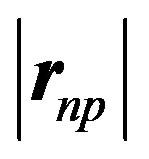 and the electric dipole moment separation distance
and the electric dipole moment separation distance 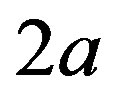 (Figures 1 and 2), are in
(Figures 1 and 2), are in :
:
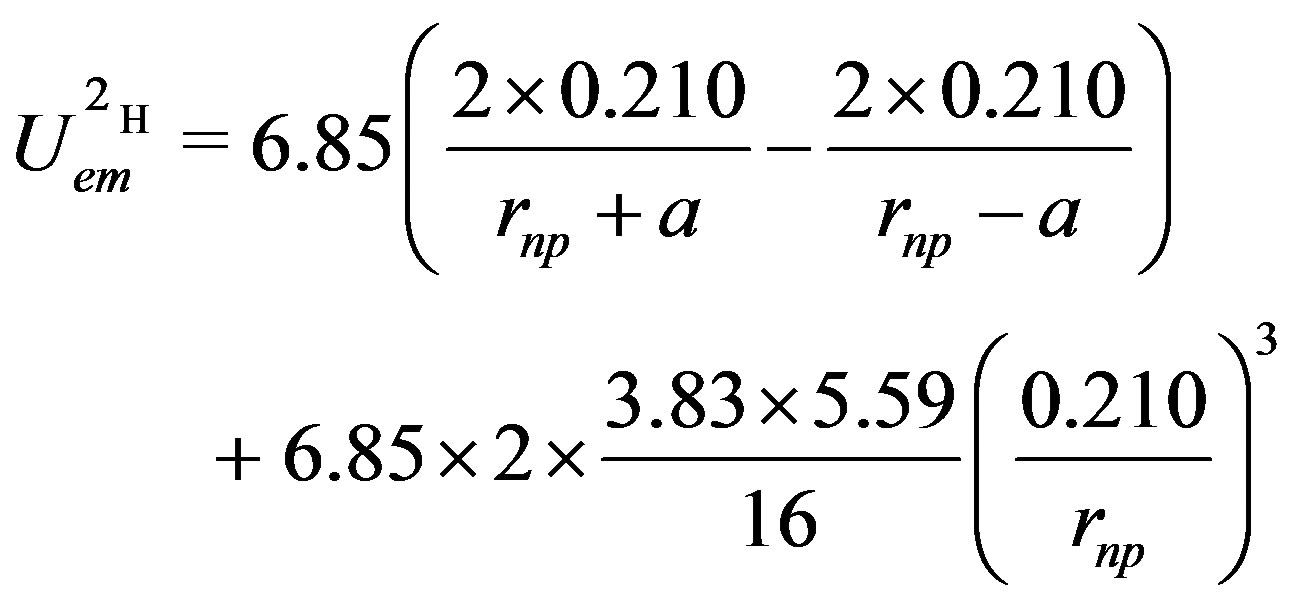 (22)
(22)
The minimum of the potential giving the binding energy for one bond, it has to be divided by two to obtain the binding energy per nucleon of the deuteron.
4.3. α Particle Electromagnetic Energy Potential
The helium  (Figure 3) has one nn, one pp and 4 np bonds. The nn bond electrostatic energy may be neglected because there is probably no electric interaction between the neutrons. The magnetic moments of the protons being collinear and opposite along the same edge, there is electric and magnetic repulsion between the protons. Because there are two protons inducing each neutron, the electrostatic potential is multiplied by 2 with respect to that of the deuteron, doubbling the electrostatic attraction. Therefore, the coefficient of
(Figure 3) has one nn, one pp and 4 np bonds. The nn bond electrostatic energy may be neglected because there is probably no electric interaction between the neutrons. The magnetic moments of the protons being collinear and opposite along the same edge, there is electric and magnetic repulsion between the protons. Because there are two protons inducing each neutron, the electrostatic potential is multiplied by 2 with respect to that of the deuteron, doubbling the electrostatic attraction. Therefore, the coefficient of  of the electrostatic terms of the neutron-proton interaction is 4 (instead of 2 for the deuteron where there is induction by only one proton on one neutron). The coefficient
of the electrostatic terms of the neutron-proton interaction is 4 (instead of 2 for the deuteron where there is induction by only one proton on one neutron). The coefficient 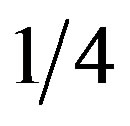 is due to the single proton-proton bond for 4 neutron-proton bonds. The electric potential per nucleon between a neutron and a proton plus between protons (between neutrons it should be 0) is, from Equation (16):
is due to the single proton-proton bond for 4 neutron-proton bonds. The electric potential per nucleon between a neutron and a proton plus between protons (between neutrons it should be 0) is, from Equation (16):
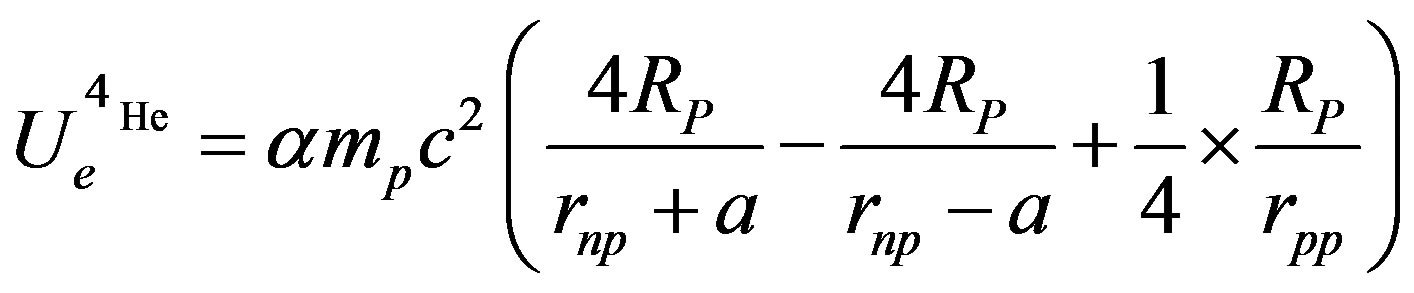 (23)
(23)
We have also to take into account the inclination between the magnetic moments. The magnetic moments of the proton and the neutron being perpendicular, the first term of (16) is zero. Being inclined at  with respect to their
with respect to their  bond, their cosines are 1/2. The projections on
bond, their cosines are 1/2. The projections on  are opposite and make an angle of 120º with
are opposite and make an angle of 120º with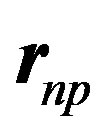 . Therefore, Formula (18) becomes:
. Therefore, Formula (18) becomes:
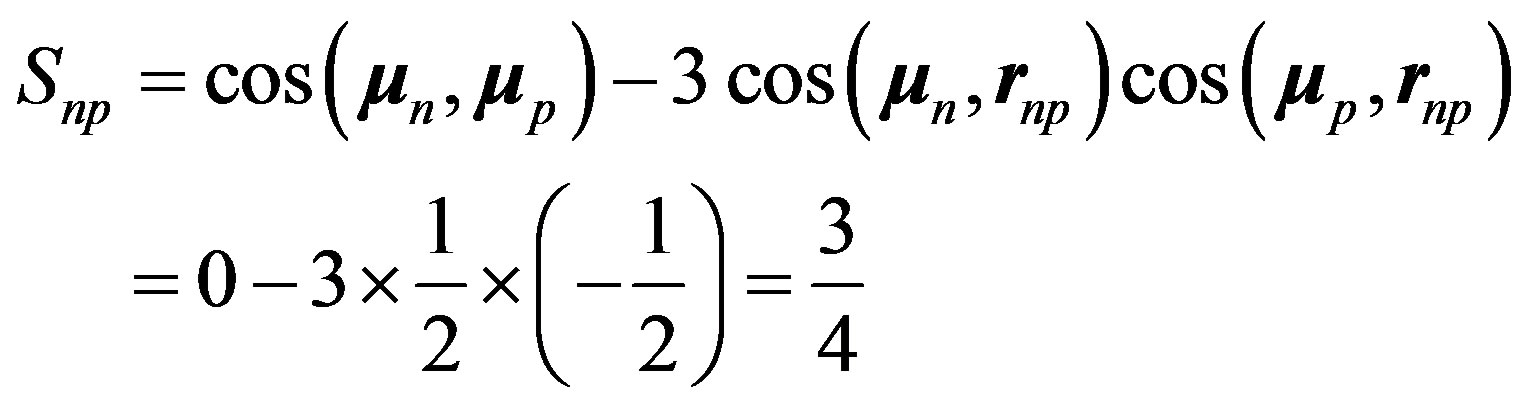 (24)
(24)
The general Formula (18) gives thus a factor 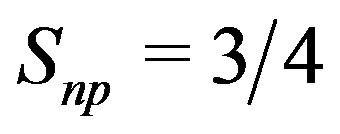 instead of 2 for the deuteron (21). The np magnetic component of
instead of 2 for the deuteron (21). The np magnetic component of  is thus 3/8 times smaller than in the deuteron. The magnetic moments of the protons being parallel and perpendicular to the straight line joining them, we have
is thus 3/8 times smaller than in the deuteron. The magnetic moments of the protons being parallel and perpendicular to the straight line joining them, we have
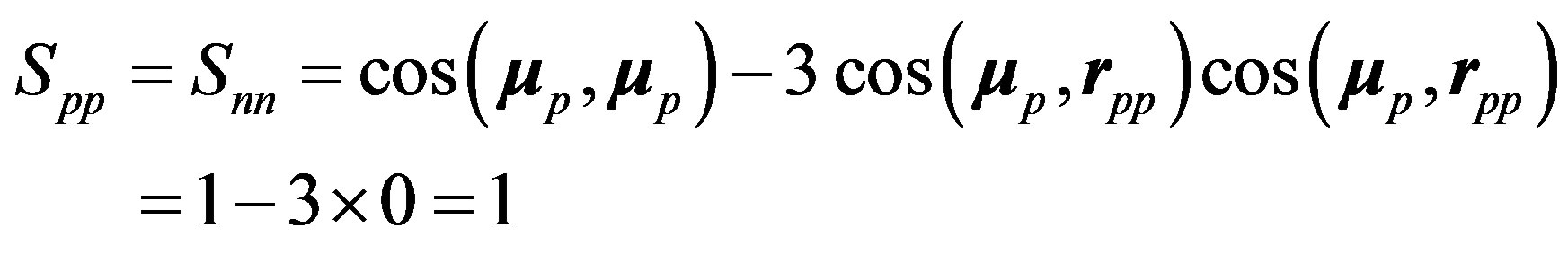 (25)
(25)
According to Formulas (24) and (25), the magnetic component of the electromagnetic potential of , for one bond (or one nucleon) is thus:
, for one bond (or one nucleon) is thus:
 (26)
(26)
The electromagnetic potential, for one bond of the 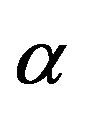 particle, is:
particle, is:
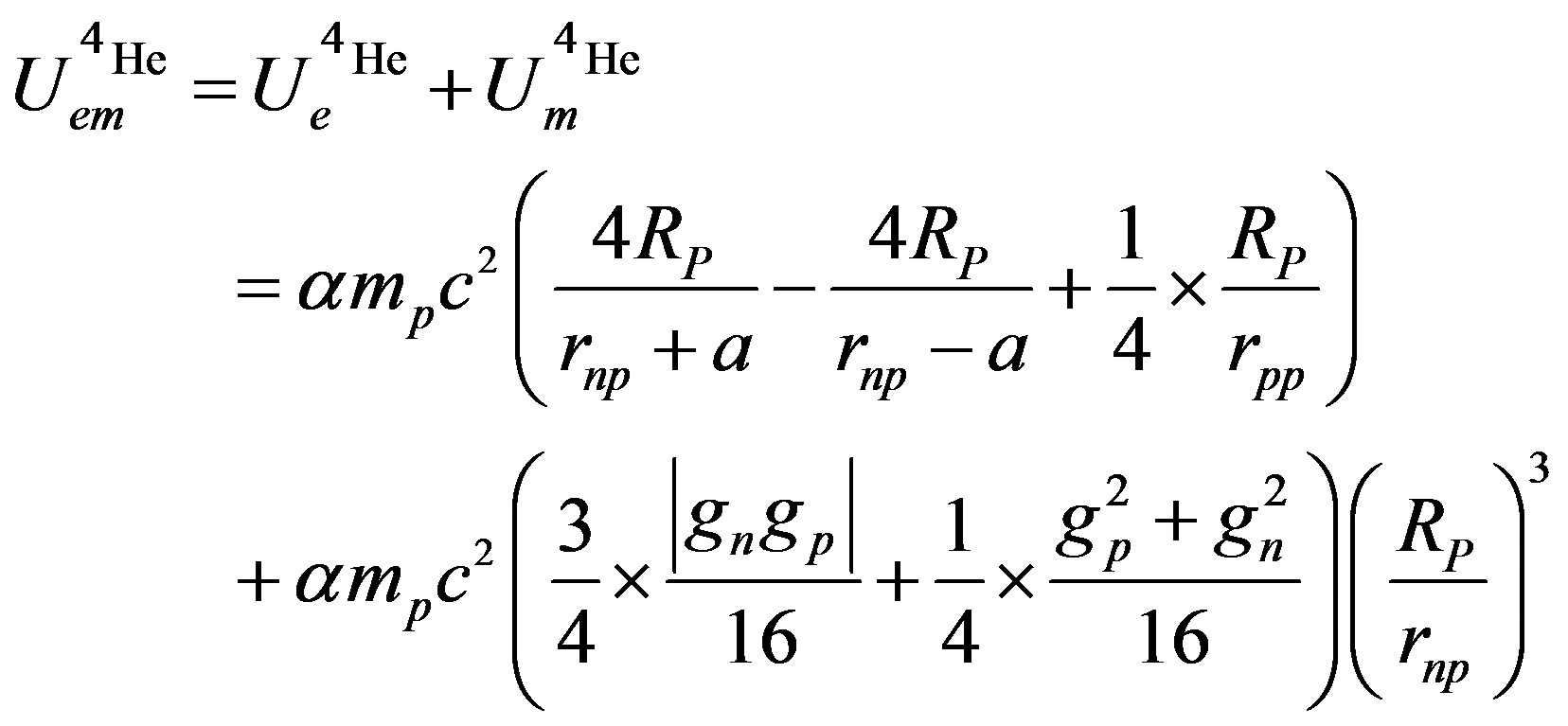 (27)
(27)
Numerically,
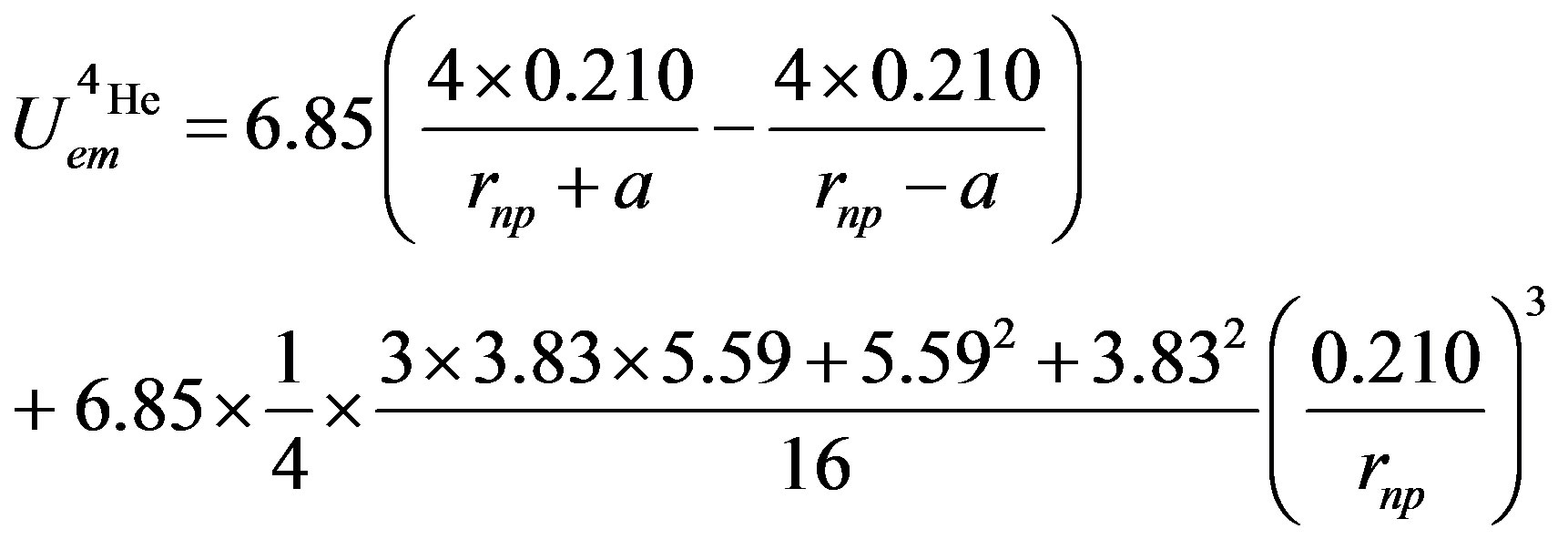 (28)
(28)
The minimum of the potential is the binding energy per nucleon, the number of neutron-proton bonds being equal to the number of nucleons.
5. Binding Energies of 2H and 4He
Because of the two variables,  , the neutron-proton separation distance and
, the neutron-proton separation distance and 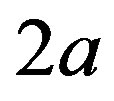 the dipole moment separation distance, the binding energy cannot be derived analytically as was done in an earlier paper [10]. It has been solved graphically by trial and error until finding the energy potential minimum for both the internucleon distance and the neutron electric dipole. Figure 4 shows that there is in fact no real minimum, only an inflection point contrarily to the first calculation of the deuteron where the minimum was clear [10]. This may be amended by taking into account the finite structure of the electric charges, perhaps by using numerical or electric image methods. The potential energies of
the dipole moment separation distance, the binding energy cannot be derived analytically as was done in an earlier paper [10]. It has been solved graphically by trial and error until finding the energy potential minimum for both the internucleon distance and the neutron electric dipole. Figure 4 shows that there is in fact no real minimum, only an inflection point contrarily to the first calculation of the deuteron where the minimum was clear [10]. This may be amended by taking into account the finite structure of the electric charges, perhaps by using numerical or electric image methods. The potential energies of  and
and  corresponding to Formulas (22) and (28) are on Figure 4, showing the agreement between experiment and theory.
corresponding to Formulas (22) and (28) are on Figure 4, showing the agreement between experiment and theory.
The binding energy per nucleon of  is found to be
is found to be 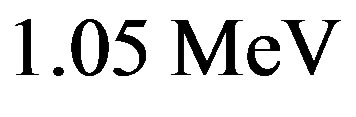 practically the experimental value 1.1 MeV.
practically the experimental value 1.1 MeV.
The calculated binding energy of  is 6.2 MeV significantly lower than the experimental value, 7.1 MeV.
is 6.2 MeV significantly lower than the experimental value, 7.1 MeV.

Figure 4. 2H and 4He electromagnetic energy potentials per nucleon from Formulas (22) and (28). The binding energies are obtained graphically by trial and error from the electric and magnetic Coulomb’s potentials by varying the neutron proton distance 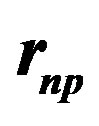 and the dipole separation
and the dipole separation 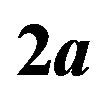 until a relative minimum is obtained, unfortunately a flat spot, due to the Coulomb singularity. A true minimum was obtained for the deuteron when the positive charge of the neutron is neglected [10]. Only fundamental constants are used, no fitting or ad hoc parameters.
until a relative minimum is obtained, unfortunately a flat spot, due to the Coulomb singularity. A true minimum was obtained for the deuteron when the positive charge of the neutron is neglected [10]. Only fundamental constants are used, no fitting or ad hoc parameters.
This discrepancy may be solved with a tetrahedron less symmetrical. Between protons and neutrons there is electric and magnetic repulsion. There is probably no electric interaction between neutrons. Its magnetic moment is smaller than that of the proton. Thus, the electromagnetic repulsion between neutrons being smaller than between protons, the separation distance should be also smaller between neutrons than between protons.
The minimum of the potential (Figure 4) occurs at  for
for  and at
and at 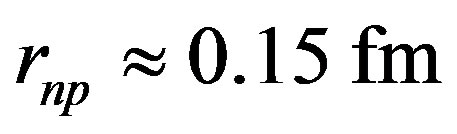 for
for 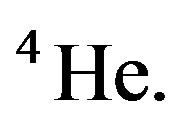 The empirical nuclear potentials of the literature give larger values, around
The empirical nuclear potentials of the literature give larger values, around 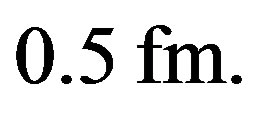
6. Discussion
The potential has a minimum when the positive charge of the neutron is neglected as was shown earlier [10]. When the dipole is taken into account, the potential has no real minimum, only a flat spot. This inflection point is due to the Coulomb singularity when the distance 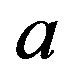 between the electric charges approaches the separation distance
between the electric charges approaches the separation distance 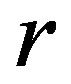 between the centers of the nucleons.
between the centers of the nucleons.
The fine structure constant 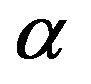 appears when the electron charge
appears when the electron charge  and the absolute dielectric permittivity of classical vacuum
and the absolute dielectric permittivity of classical vacuum 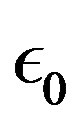 are replaced by the proton mass, the light velocity
are replaced by the proton mass, the light velocity  and the proton Compton radius
and the proton Compton radius . Although
. Although  is 4 times smaller than the measured proton radius,
is 4 times smaller than the measured proton radius, 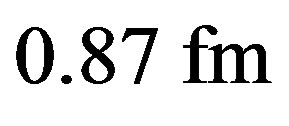 and half the usual value of the radial minimum of the nucleon-nucleon potential energy, usually around
and half the usual value of the radial minimum of the nucleon-nucleon potential energy, usually around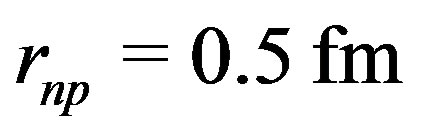 . The calculations give good results for the binding energies without needing any ad hoc parameter.
. The calculations give good results for the binding energies without needing any ad hoc parameter.
In the deuteron, the magnetic moments of the proton and the neutron are opposite because the magnetic moment of the deuteron is, approximately, the difference between the absolute values of the proton and neutron magnetic moments. When the magnetic moments are collinear, the proton and the neutron rotate around their common axis, stabilized by the gyroscopic effect due to the nucleon spin.
The calculated binding energy of  is still
is still 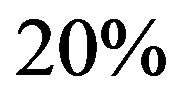 too weak. Indeed, the symmetry of
too weak. Indeed, the symmetry of  is not that of a regular tetrahedron because there are two kinds of nucleons with different electric and magnetic properties. A more precise calculation will be performed as soon as possible, taking into account a lower symmetry of the tetrahedron.
is not that of a regular tetrahedron because there are two kinds of nucleons with different electric and magnetic properties. A more precise calculation will be performed as soon as possible, taking into account a lower symmetry of the tetrahedron.
7. Results
The following results have been obtained by applying the electromagnetic theory to the atomic nucleus:
• The nuclear attraction between a neutron and a proton is the electrostatic induction of a proton on a nearby neutron.
• The soft core is the repulsion between the magnetic moments of the nucleons.
• The calculated binding energies of the deuteron and of the 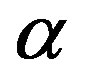 particle agree satisfactorily with the experimental data.
particle agree satisfactorily with the experimental data.
• A nuclear equivalent of the Rydberg constant, 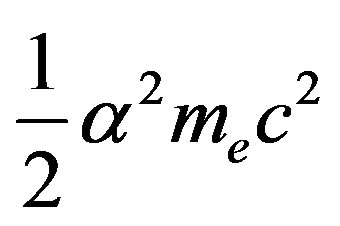 has been found to be
has been found to be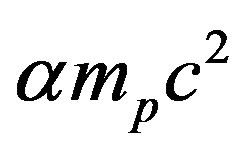 .
.
• The ratio between nuclear and chemical energy is discovered to be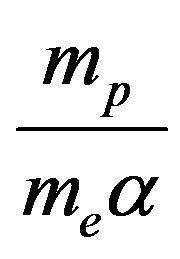 .
.
8. Conclusion
The electric and magnetic Coulomb’s laws applied to the nucleons (without orbital angular momenta) suffice to predict quantitatively the nuclear interaction as the achievement of the  and
and  binding energies proves it, the calculations being easily verifiable. The agreement with experiment confirms the electromagnetic nature of the nuclear interaction found in a preceding paper [10]. Taking into account the neglected interactions in
binding energies proves it, the calculations being easily verifiable. The agreement with experiment confirms the electromagnetic nature of the nuclear interaction found in a preceding paper [10]. Taking into account the neglected interactions in  should enhance its binding energy precision. In contrast, the hypotheses of charge independence, strong force and shell model are unable to calculate
should enhance its binding energy precision. In contrast, the hypotheses of charge independence, strong force and shell model are unable to calculate , the simplest nucleus beyond the proton and a fortiori
, the simplest nucleus beyond the proton and a fortiori . It is hoped to generalize the electromagnetic approach to all nuclei.
. It is hoped to generalize the electromagnetic approach to all nuclei.
REFERENCES
- D. R. Lide, “Handbook of Chemistry and Physics,” 86th Edition, CRC Press, Boca Raton, 2005.
- R. Feynman, R. B. Leighton and M. Sands, “The Feynman Lectures on Physics 2,” Pearson/Addison-Wesley, Reading, 2006.
- G. Gamow, “Les Noyaux Atomiques,” Annales de l'Institut Henri Poincaré, Vol. 5 1935, pp. 89-114.
- F. Bloch, “Le Moment Magnétique du Neutron,” Annales de l'Institut Henri Poincaré, Vol. 8, 1938, pp. 63-78.
- J. C. Maxwell, “A Treatise on Electricity and Magnetism,” Dover Publications Inc., New York, 1954.
- C. Q. Choi, “Not So Neutral Neutron,” Scientific American, Vol. 297, No. 6, 2007, p. 37. doi:10.1038/scientificamerican1207-37c
- G. E. Owen, “Introduction to Electromagnetic Theory,” Courier Dover Publications, Oxford, 2003.
- K. Yosida, “Theory of magnetism,” Springer-Verlag, Berlin, 1996.
- V. F. Weisskopf and J. M. Blatt, “Theoretical Nuclear Physics,” Courier Dover Publications, New York, 1991.
- B. Schaeffer, “Electromagnetic Theory of the Binding Energy of the Hydrogen Isotopes,” Journal of Fusion Energy, Vol. 30, No. 5, 2011, pp. 377-381. doi:10.1007/s10894-010-9365-0
• Appendix: Fundamental Constants Used
• Fine structure constant
 (29)
(29)
• Proton Compton radius
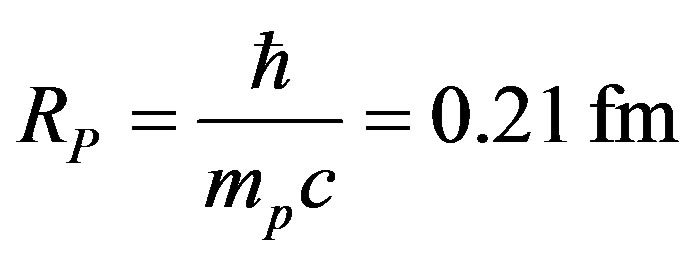 (30)
(30)
• Nuclear magneton
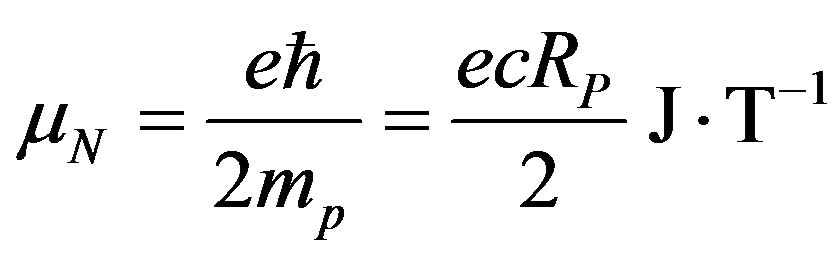 (31)
(31)
• Magnetic moments of the neutron and the proton  and
and 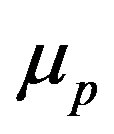 and their corresponding Landé factors,
and their corresponding Landé factors, 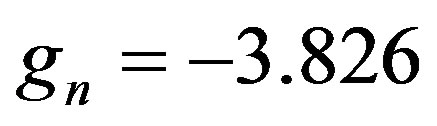 and
and , are related by
, are related by
 (32)
(32)
where i means n or p.
• Relation between vacuum dielectric permittivity and magnetic permeability
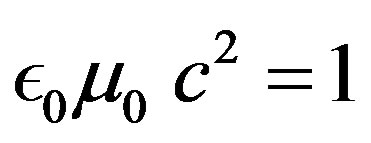 (33)
(33)
• Fundamental constants of the nuclear energy potential Electrostatic attraction:
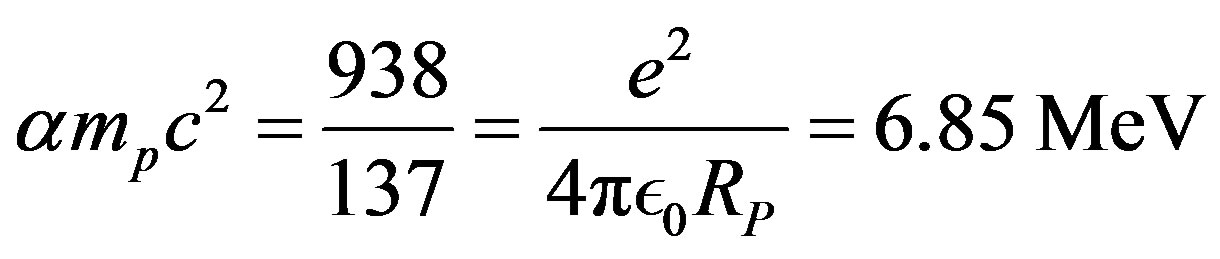 (34)
(34)
4% weaker than the  particle binding energy per nucleon
particle binding energy per nucleon .
.
Magnetic repulsion:
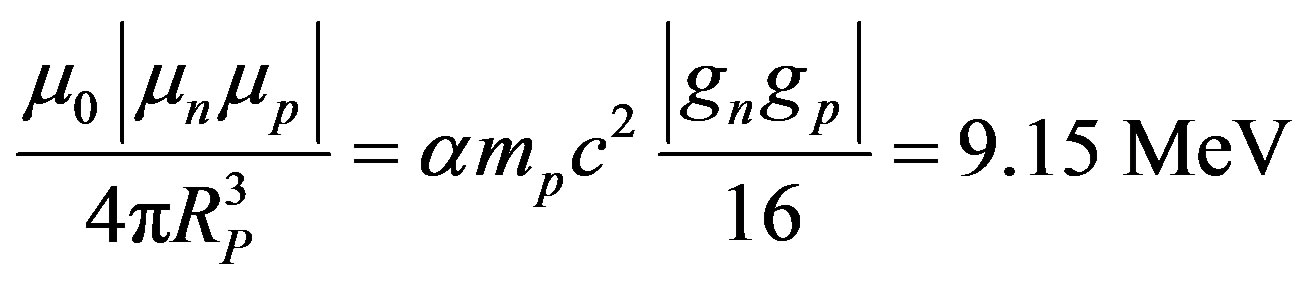 (35)
(35)
where  and
and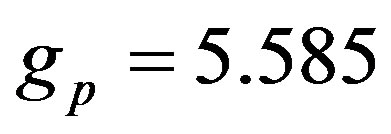 .
.

