Journal of Modern Physics
Vol.3 No.6(2012), Article ID:20084,9 pages DOI:10.4236/jmp.2012.36060
Dissipative Discrete System with Nearest-Neighbor Interaction for the Nonlinear Electrical Lattice
1Département des Sciences Physiques, Ecole Normale Supérieure, Université de Maroua, Maroua, Cameroon
2Laboratory of Mechanics, Department of Physics, Faculty of Science, University of Yaounde I, Yaounde, Cameroon
3Ecole Nationale Supérieure Polytechnique, Université de Yaounde I, Yaoundé, Cameroon
4Department of Physics, Faculty of Science, University of Ngaoundéré, Ngaoundéré, Cameroon
5Department of Physics, Periyar University, Salem, India
6Condensed Matter Laboratory, Department of Physics, Faculty of Science, University of Douala, Douala, Cameroon
Email: elsaidais@yahoo.fr, *mohdoufr@yahoo.fr
Received February 2, 2012; revised February 25, 2012; accepted March 2, 2012
Keywords: Generalized dissipative discrete complex Ginzburg-Landau equation; discrete Lange Newell-criterion; pulse trains; solitary patterns
ABSTRACT
A generalized dissipative discrete complex Ginzburg-Landau equation that governs the wave propagation in dissipative discrete nonlinear electrical transmission line with negative nonlinear resistance is derived. This equation presents arbitrarily nearest-neighbor nonlinearities. We analyze the properties of such model both in connection to their modulational stability, as well as in regard to the generation of intrinsic localized modes. We present a generalized discrete Lange-Newell criterion. Numerical simulations are performed and we show that discrete breathers are generated through modulational instability.
1. Introduction
During these last decades the behavior of nonlinear discrete systems has received considerable attention in many areas of physics. The nonlinear electrical transmission lines (NLTLs) are good examples of such systems. They are very convenient tools for studying quantitatively the fascinating properties of wave propagation in nonlinear dispersive media. Afshari and Hajimiri [1] have introduced and analyzed pulse narrowing and edge sharpening passive NLTL, using accumulation mode metal-oxide semiconductor varactors and the gradual scaling lines, showing simultaneous edge sharpening for both rising and falling edges in silicon. The experimental results show considerable improvement in the rise and fall times of the pulses. These lines can have applications in ultrawideband systems, broadband signal generations, and highspeed serial communications [2-4]. The problem of a wide pulse degenerating into multiple pulses rather than a single pulse is solved by using a gradually scaled NLTL. The ability of solitons to propagate with small dispersion can be used as an effective means to transmit data, modulated as short pulses over long distances; one example of this is the ultra wideband impulse radio that has recently gained popularity [5]. More recently, the experimental, analytical and numerical study of a lefthanded nonlinear electrical lattice have been performed by English et al. [6]. They found that the above system clearly supports backward wave propagation of plane waves, but also envelope solitons of the bright and dark type. From the viewpoint of NLTL experiments, pulse propagation [7] and envelope soliton formation [8] were recently studied (see also the review of Ref. [9]), while pertinent theoretical works, based on the use of a nonlinear Schrödinger (NLS) equation, allowed the description of bright [10] or dark [11] envelope solitons observed in the experiments. One of the best mechanism to generate solitonlike excitation is through the modulational instability (MI).
Thus far, discrete spatial solitons (nonlinear eigenstates) have been successfully demonstrated in NLTL [12-15]. Like every nonlinear system, a NLTL can exhibit an instability that leads to a self-induced modulation of input plane wave with the subsequence generation of localized pulses [16-19]. This phenomenon is known as a Benjamin-Feir modulational instability [20] and it is responsible of many physically interesting effects such as the formation of envelope solitons. In homogeneous nonlinear systems, MI may be considered as the leading mechanism for energy localization as well as the formation of traveling intrinsic localized modes [21,22]. The corresponding mathematical model is the NLS equation or the complex Ginzburg-Landau (CGL) equation with periodically varying dispersion and nonlinear coefficients. The CGL describes the long wavelength modulations (envelopes or amplitudes) of both travelling waves and homogeneous oscillations. This equation has a wide range of applications.
Dissipative phenomena in nonlinear media with complex parameters are attracting nowadays a great deal of attention. In the present work we shall address these problems with a twofold aim. From one side, we derive the discrete CGL (DCGL) equation with nearest-neighbor nonlinearities which governs the propagation of wave in the DNLTL. From the other side, we show that the derived equation can be used to explore interesting dynamical behaviors as generate nonlinear localized modes in the DNLTL. To this regard we investigate the MI as a mechanism of the generation of bright matter-waves in the DNLTL. Dissipation is one of the main forces acting against the formation of nonlinear coherent structures in extended systems. When dissipation is present in systems without additional gain mechanisms, typically all excitations decay into the regime of linear waves.
The work is organized as follows. In section 2, the analytical model based on the DNLTL is presented and we derived the DCGL equation with nearest-neighbor nonlinearities. Then, we present a qualitative analysis concerning MI and we propose the generalized LangeNewell criterion. In section 3, since the discrete breathers solutions with small amplitudes are very close to plane waves, we focuse on the generation of nonlinear excitations induced by MI. Finally, conclusions are drawn in Section 4.
2. The DCGL Equation with Nearest-Neighbor Nonlinearities in the Nltl
Many schematic electrical lattices have already been consider in the litterature. Recently, a one dimensional biinductance lattices which act as band-pass filters has been considered [23]. Authors of [12,13] consider an original capacitor which has the purpose to block dc current from flowing through the resistor and inductor to the ground in the case where the driver contained a dc voltage offset. This description is only correct in the linear and weakly nonlinear regime, but does not hold in the fully nonlinear regime. The main point (captured both by the experimental and numerical traces) is that the blocking capacitor does not alter the linear and weakly nonlinear properties of the lattice, but that it certainly does affect the strongly nonlinear regime in the dynamics. But, the attenuation of waves is due to dissipative effects of the medium in which they travel. We are interested in the study of the propagation of nonlinear localized modes in a nonlinear transmission line by doping the line with negative nonlinear resistance. Analytical results and numerical simulation have shown that the attenuated wave recovers its amplitude on a short distance of the doped domain. So, the original purpose of this negative nonlinear resistance is the particular functional form of the capacitor which should amplify the waves after attenuation. It has been shown that the wave conserves its pulse form when crossing the amplification domain [24].
So, here we consider a nonlinear network of N cells as illustrated in Figure 1. Each cell contains a linear inductor Ls in the series and shunt branch and a linear inductor Lp in parallel with a nonlinear capacitor Cp in the shunt branch. This capacitor is the well-known bias-dependent responsible for nonlinearity of the system. Its capacitance is assumed to be expanded as a power series of the local signal voltage Vn, which appears across the nonlinear capacitor of the nth cell
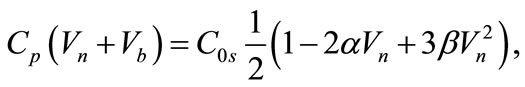 (1)
(1)
where, C0p is a constant corresponding to the capacitance of the nonlinear diode at the dc bias-voltage Vb. The nonlinear parameters α and β are assumed to be positive constants. In Equation (1), we keep nonlinear coefficient up to the second order for the following reasons. First, the polynomial approximation of the C-V curve and corresponding fit are justified if the voltage amplitude is small enough. Second, in this voltage range, to reduce the equation of motion to an ordinary differential equation, it is sufficient to take into account these two terms, only, to balance the first-order dispersion term. Having in mind that the compactification of solitary wave results from the nonlinear dispersion of the system, we have to choose the dispersion element properly in order to assure

Figure 1. Schematic representation of the NLTL.
that the resulting network will satisfy this requirement. It has been pointed out by Comte and Marquié [25] that the introduction of the nonlinear resistor in the series branch of the nonlinear transmission line modelling the propagation of fluxons in reaction-diffusion chain can create a nonlinear dispersion and then the compactification of kink solitons. Here, the introduction of the voltage dependence in the capacitor in the series branch can make circuits that perform a variety of tasks and probably the compactification of envelope solitary waves. Thus, the capacitance-voltage relationship in the series branch is Taylor expanded to second order and reads:
 (2)
(2)
where V is the voltage across the nonlinear capacitor with the zero-voltage value C0s. So, the operating point of this capacitor corresponds to the zero-voltage value. In order to take in to account the dissipation of the network, the conductance g is connected in parallel with Cp and Lp, respectively. The conductance g accounts for the dissipation of the inductor Lp in addition to the loss of the nonlinear capacitor C. The corresponding conductance g is given by [24]
 . (3)
. (3)
The linear dispersion relation of the line is a typical band pass filter:
 (4)
(4)
where, 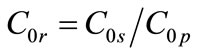 ,
,  and
and 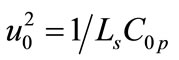 , are the dimensionless capacitance and characteristic frequencies of the system. The corresponding linear spectrum has a gap f0 = ω0/2π and it is limited by the cut-off frequency
, are the dimensionless capacitance and characteristic frequencies of the system. The corresponding linear spectrum has a gap f0 = ω0/2π and it is limited by the cut-off frequency , with
, with 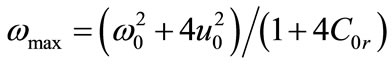 due to lattice effects. The linear dispersion curve of the network is plotted in Figure 2 as a function of the wave vector k (rad/cell). From Equation (4), one can derive the following group velocity:
due to lattice effects. The linear dispersion curve of the network is plotted in Figure 2 as a function of the wave vector k (rad/cell). From Equation (4), one can derive the following group velocity:
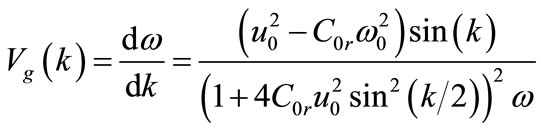 (5)
(5)
This group velocity is represented in Figure 3. We restrict our study to slow temporal variations in the envelope. As we shall see, it provides a deep and useful insight into the full dissipative dynamics of the nonlinear electrical line and leads to pattern formation.
Applying Kirchhoff’s laws to this system leads to the following set of differential equations governing wave propagation in the network
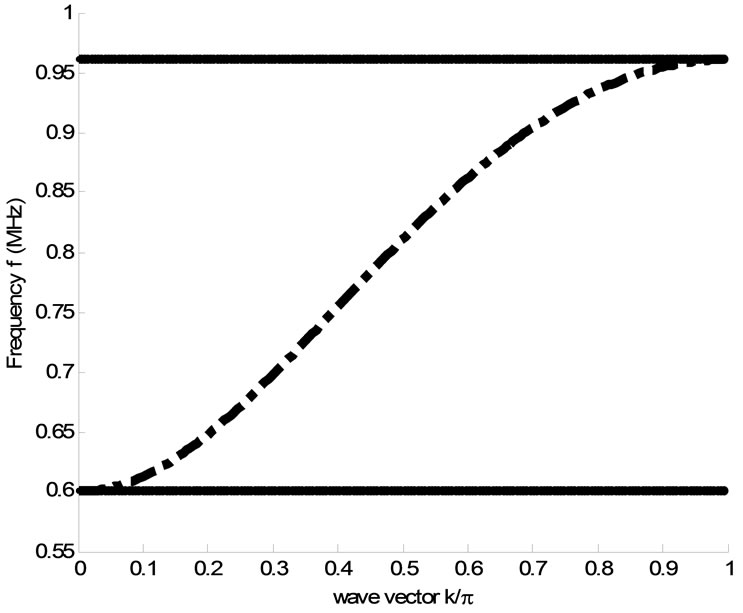
Figure 2. Linear dispersion curve of the lattice: frequency f = ω/2π (MHz) as a function of wave vector k (rad/cell). The characteristic frequencies of the network and reduced capacitance are ω0 = 3.77 × 106 rad/s, u0 = 2.58 × 106 rad/s and C0r = 0.03, respectively.
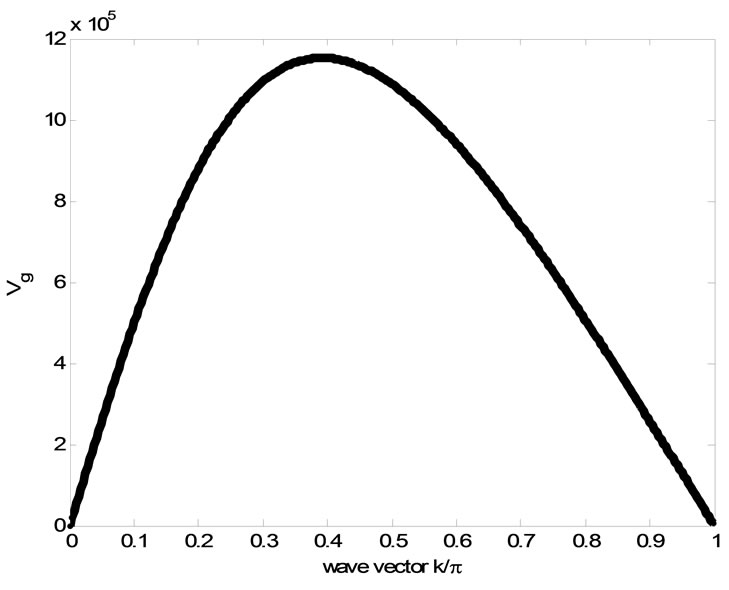
Figure 3. Group velocity.
 (6)
(6)
with,  and
and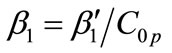 . For this purpose, restricting moreover our study to weak amplitude and slow temporal variations of the wave envelope, we look for a solution of Equation (6) in the form
. For this purpose, restricting moreover our study to weak amplitude and slow temporal variations of the wave envelope, we look for a solution of Equation (6) in the form
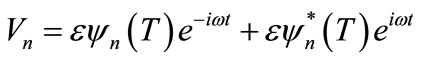 , (7)
, (7)
where 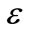 is small parameter (
is small parameter ( ) and
) and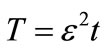 ,
, 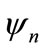 is unknown complex envelope function,
is unknown complex envelope function, 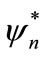 stands for complex conjugate and ω denoting frequency. Inserting this relation in Equation (6), we collect solutions of order
stands for complex conjugate and ω denoting frequency. Inserting this relation in Equation (6), we collect solutions of order 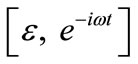 which give a relation between the wave function at different site of the lattice. Thereafter, one can write the relation at order
which give a relation between the wave function at different site of the lattice. Thereafter, one can write the relation at order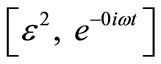 , using the dispersion relation [Equation (4)] and equations resulting from the above different order, one obtains the following equation:
, using the dispersion relation [Equation (4)] and equations resulting from the above different order, one obtains the following equation:
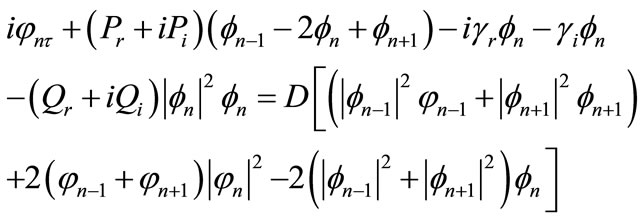 (8)
(8)
where the complex coefficients of Equation (8) are given by
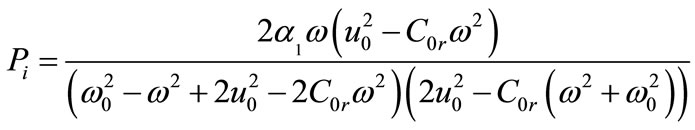
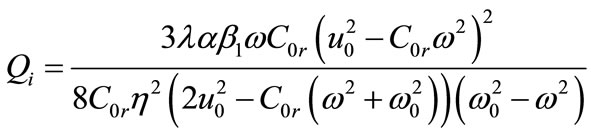


Equation (8) is the DCGL equation with nearestneighbor nonlinearities. Note that the DCGL equation has been phenomenologically proposed to describe frustrated states in a linear array of vortices [26,27]. Also, it reproduces reasonably well characteristics of the turbulent regime below the percolation threshold. Percolation has been found to be a useful concept for the description of turbulence, and the results suggest that non adiabatic effects, such as discrete nature of the system, play a role in the system. From a physical point of view, it is of interest to study the effects of including nearest-neighbor nonlinearities terms than cubic in the equation on discrete solitons. These terms appear in different physical contexts such as Bose gases with hard core interactions in the Tonks-Girardeau regime [28] and low dimensional Bose-Einstein condensates in which quintic nonlinearities in the NLS equation are used to model three-body interactions [29]. A self-focusing cubic-quintic NLS equation is also used in nonlinear optics as a model for photonic crystals [30].
In particular when the nearest-neighbor parameter D = 0, Equation (8) becomes the well-known DCGL equation [31], and for Pi = Qi = γr = D = 0, Equation (8) is reduced to the usual (nonintegrable) discrete nonlinear Schrödinger equation [32,33].
Modulation instability is a generic nonlinear phenomenon governing nonlinear wave propagation in dispersive media. It refers to a weak space-time dependence (modulation) of the wave amplitude, due to intrinsic medium nonlinearity, however weak. Under the effect of external perturbations (e.g., noise), the wave amplitude (the envelope) may potentially grow, eventually leading to energy localization via the formation of localized structures (envelope solitons) [34].
To analyze MI, which is responsible for energy localization, we seek a solution of Equation (8) in the form of plane wave disturbed as follow
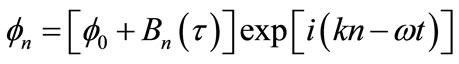 (9)
(9)
where f0 is the initial complex constant amplitude, k and ω are, respectively, the wave number and the angular frequency of the carrier wave. The quantity Bn(τ) is the perturbation assumed to be small in comparison with the amplitude of the carrier wave. It would be important to ask what happens to the plane waves when the amplitude increases sufficiently so that the nonlinearity occurs. In the linear approximation an equation for Bn(τ) yields the dispersion relation for the evolution of small perturbations,
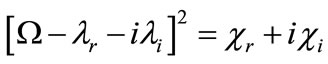 , (10)
, (10)
where λr, λi, χr, and χi are defined in the Appendix. The frequency Ω can be written as
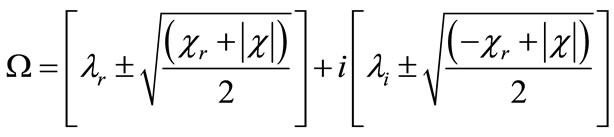 (11)
(11)
Equation (11) has been established for the case . We easily get the perturbation as follow
. We easily get the perturbation as follow
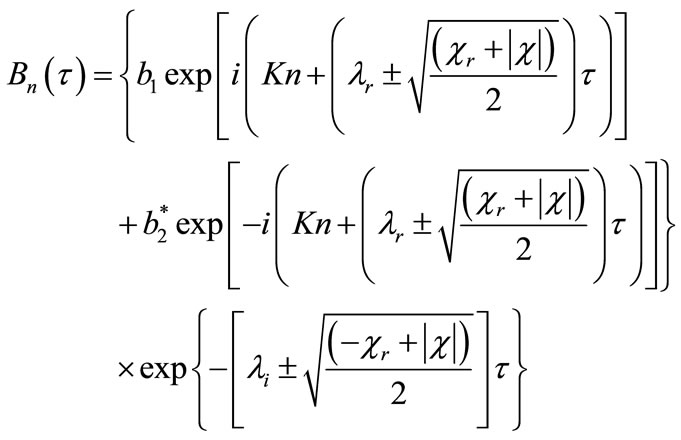 (12)
(12)
where K, b1 and b2 are the wave number and the complex constants, respectively.
The amplitude Bn will be unbounded as 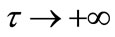 if and only if:
if and only if: 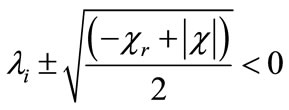 , in order to get this relation, it is necessary that λi < 0. Because,
, in order to get this relation, it is necessary that λi < 0. Because, 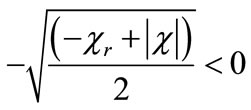 , the relation,
, the relation, 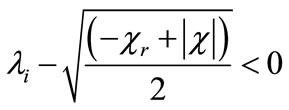 holds and from this inequality we can easily derive the following inequality,
holds and from this inequality we can easily derive the following inequality,
 (13)
(13)
Relation (13) represents the amplitude threshold , for the MI versus the wave number k of the carrier wave and the K of the perturbation for the dissipative coefficients: α1 = 2.6710 × 104 Ω−1·F−1 (see Figure 4).
, for the MI versus the wave number k of the carrier wave and the K of the perturbation for the dissipative coefficients: α1 = 2.6710 × 104 Ω−1·F−1 (see Figure 4).
Assume that the necessary condition 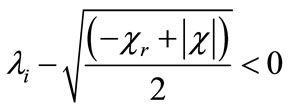 , is satisfied, then we can write the inequality
, is satisfied, then we can write the inequality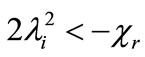 , that is
, that is
 (14)
(14)
Relation (14) represents the MI criterion associated with the DCGL equation with higher-order nonlinearities.
This result is the generalized Discrete Lange and Newell criterion for Stokes waves.
The growth rate of the perturbation is given by Ωi. This quantity has been plotted in Figure 5.
From this figure, one can see that our system can be really stable unstable (the two branches).
3. Generation of Intrinsic Localized Modes
Let us check the theoretical predictions concerning the existence of MI in the system. So, to further explore MI, we compute numerical simulations. In particular, our results are based on the theory of linear stability analysis. However, we know that the linear stability analysis is limited because it can only predict the onset of instability and does not tell us anything about the long-time dynamical behavior of the system when the instability grows. When the perturbation amplitude grows large enough compared to that of the initial wave, the numerical analysis must be adopted. To further confirm that the linear instability analysis given above can correctly describe the initial stage of instability, we have performed numerical simulations of Equation (1). A fourth-order Runge-Kutta algorithm has been used. A normalized
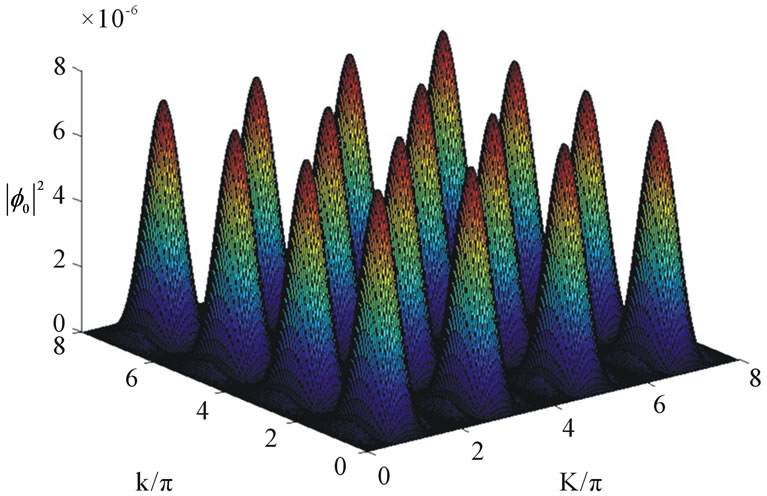
Figure 4. Treshold amplitude on the (K, k) plane. Pi = 0.0141, Qi = −1.6681.
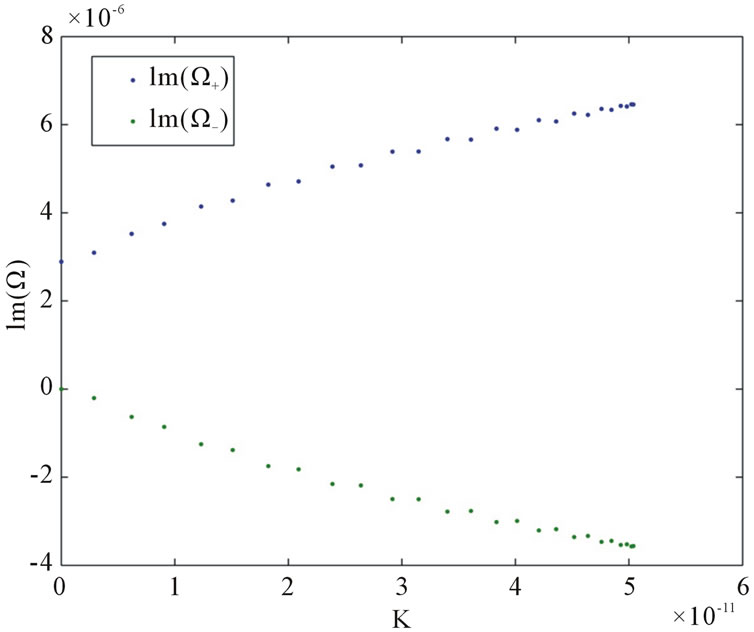
Figure 5. Imaginary part of Ω for k = π.
integration time step Δt = 5 × 10−3 is used for numerical simulations. Similarly, the number of cells N is chosen to be equal to 1600 and we have used periodic boundary conditions so that we do not encounter the wave reflection at the end of the line. The parameters of the system are choosen in accordance with Figure 2 as well as with Equation (14). At the input of the line, we apply a slowly modulated signal located at n0 = 100,
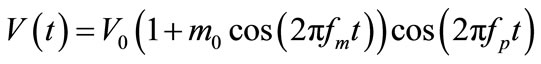 (15)
(15)
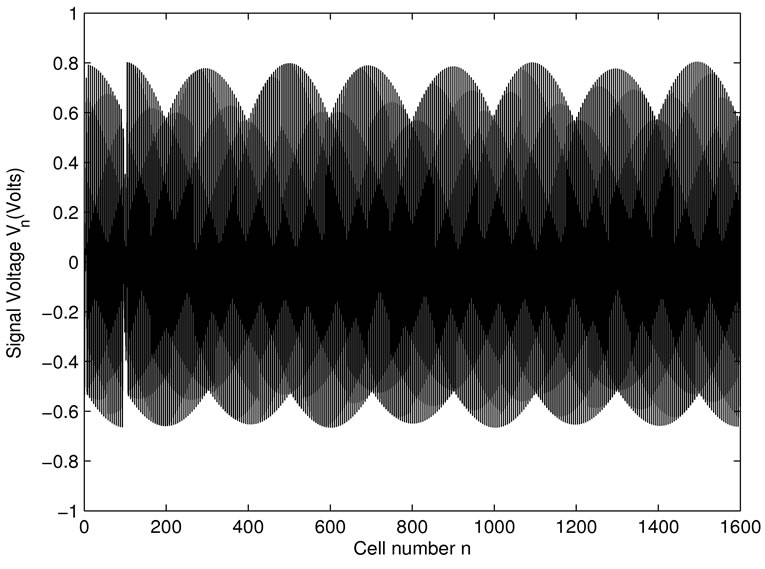
where, V0 is the amplitude of the unperturbed plane wave, m0 designates the modulation rate and fm the frequency of modulation. MI has been analyzed for lattices with respect to discrete breathers. As a specific example, we use the following value V0 = 0.90 V, fp = 800 kHz, m0 = 0.01 and fm = 8 kHz. Then, we launch solution (15) in the network. As time goes on, the modulation increases and the continuous wave breaks into a periodic pulse or envelope soliton train as shown in Figure 6(a) at time t = 1000. A soliton is a localized wave form that travels along the system with constant velocity and underformed shape. It is well known that in transmission media supporting solitons, any input pulse with a duration greater than soliton width tends to dissolve into a superposition of solitons. In this regard, a sinusoidal signal fed to the NLTL will progressively decompose into multiple solitons per cycle, and harmonics of the input frequency will be obtained at the output as viewed in Figure 6(b). This figure has been obtained for the parameters fm = 8 kHz, fp = 750 kHz and k = 0.9π , one sees that as time goes on, the modulation increases and the initial continuous wave breaks into a periodic pulses soliton train at time t = 375. The amplitude of the wave generated by wave motion is modulated in the form of a train of small amplitude with a short wavelength. Each component of the train has the shape of a soliton like object.
 (a)
(a)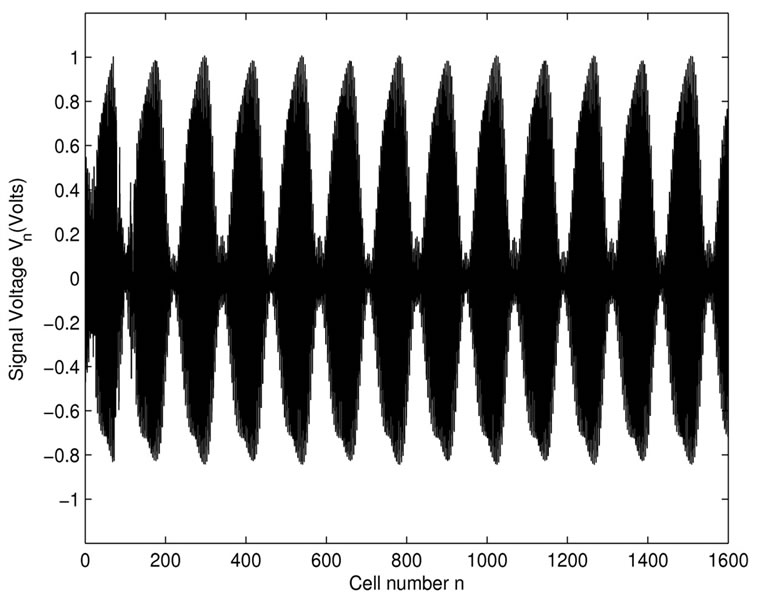 (b)
(b)
Figure 6. Space evolution of the amplitude showing the dynamics of the pulse. The pulse undergoes periodic oscillations in the vicinity of the stable intersite configuration. V0 = 0.90 V, m0 = 0.01. (a) at time t = 1000 for fp = 800 kHz, and fm = 8 kHz; (b) at time t = 375 for fm = 8 kHz and fp = 750 kHz.
Figure 7 shows the development of nonlinear wave packets with a slowly varying envelope in space with regard to a given carrier wave with frequency fp = 750 kHz, fm = 16 kHz and the modulated wave number k = 0.9π at time t = 750. One sees the appearence of envelope solitons related to the existence of MI in the NLTL. One obtains an interesting phenomenon: the wave displays an oscillating and breathing wave behavior. In nonlinear physical systems with discrete symmetry, which is considered to be as fundamental as the concepts of solitons, dissipative structures, etc. in modern nonlinear science the concept of bushes of normal modes could be applied. The phenomenon observe in Figure 7 can be also explained by the theory of “bushes” of nonlinear normal modes [35-37]. Since the symmetry-determined bushes are valid for any of monatomic chains and, in some sense, they can be applied to multiatomic chains as well, one can describe these phenomena as bushes. As an indivisible nonlinear object, the bush exists because of force interactions between the modes contained in it. Apparently, bushes of modes play an important role in many physical phenomena of current interest [35-37].
4. Conclusions
In this work, we have introduced the generalized discrete complex Ginzburg-Landau equation with nearest-neighbor nonlinearities in the nonlinear discrete transmission lattices. The appearence of MI has been investigated and the generalized discrete Lange-Newell proposed. The theoretical findings have been numerically tested through direct simulations and solitonic excitations of the pulse train have been generated. The theory of “bushes” of nonlinear normal modes has been also point out.
The MI is the first step in the generation of soliton like excitations in physical systems. Therefore the study of
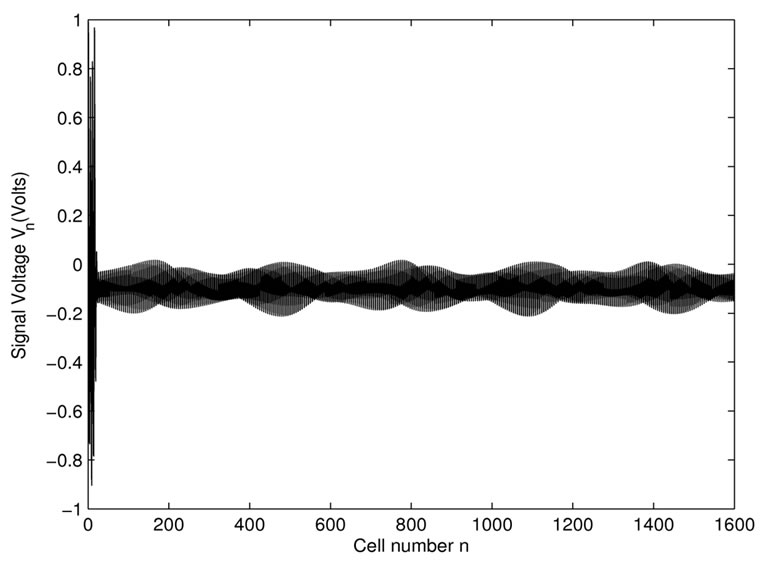
Figure 7. Desintegration of the initial periodic solution into a wave train at t = 750 for k = 0.9π, fp = 750 kHz and fm = 16 kHz.
the conditions in which this phenomenon takes place is of special importance. This result is very useful for either the investigation of nonlinear transmission lines or of there similar physical problems, such as nonlinearity, in the plasma, dusty plasma, Bose-Einstein condensates, etc.
Finally, it is important to mention that, in recent years, the development in NLTL has demonstrated its capacity to work as signal processing tools. To cite only very few examples, it has been demonstrated that the nonlinear uniform electrical line can be used for extremely wide band signal shaping applications [2] as well as a wave form equalizer in the compensation scheme for signal distortion caused by optical fiber polarization dispersion mode. Moreover, it is also possible to use NLTLs in the scheme for controlling the amplitude (amplification) and the delay of ultrashort pulses through the coupled propagation of the solitonic and dispersive parts, which is important in that it enables the characterization of highspeed electronic devices such as hetero-junction field effect transistor or resonant tunneling diodes, and raises the possibility of establishing future ultra-high signal processing technologies. Besides its practical interests, it is well known that NLTLs are convenient tools for the study of wave propagation in nonlinear dispersive media. In particular, they provide a useful way to check how the nonlinear excitation behaves inside the nonlinear medium and to model the strange properties of new systems.
5. Acknowledgements
A.M is very grateful for the hospitality of the CMSPS of the Abdus Salam ICTP of Trieste-Italy.
REFERENCES
- E. Afshari and A. Hajimiri, “Nonlinear Transmission Lines for Pulse Shaping Silicon,” IEEE Journal of SolidState Circuits, vol. 40, No. 3, 2005, pp. 744-752. doi:10.1109/JSSC.2005.843639
- E. Afshari, H. S. Bhat, A. Hajimiri and J. E. Marsden, “Extremely Wideband Signal Shaping using One and Two Dimensional Non-Uniform Nonlinear Transmission Lines,” Journal of Applied Physics, vol. 99, No. 5, 2006, Article ID: 054901. doi:10.1063/1.2174126
- H. S. Bhat and B. Osting, “The Zone Boundary Mode in Periodic Nonlinear Electrical Lattices,” Physica D, Vol. 238, No. 14, 2009, pp. 1216-1228. doi:10.1016/j.physd.2009.04.009
- H. S. Bhat and E. Afshari, “Nonlinear Constructive Interference in Electrical Lattices,” Physical Review E, Vol. 77, No. 6, 2008, Article ID: 066602. doi:10.1103/PhysRevE.77.066602
- R. A. Scholtz, “Signal Selection for the Indoor Wireless Impulse Radio Channel”, IEEE 47th Vehicular Technology Conference, Vol. 3, 1997, pp. 2243-2247.
- L. Q. English, S. G. Wheeler, Y. Shen, G. P. Veldes, N. Whitaker, P. G. Kevrekidis and D. J. Frantzeskakis, “Backward-Wave Propagation and Discrete Solitons in a Left-Handed Electrical Lattice,” Physics Letter A, Vol. 375, No. 9, 2011, pp. 1242-1248. doi:10.1016/j.physleta.2011.01.042
- A. B. Kozyrev, H. Kim, A. Karbassi and D. W. van der Weide, “Wave Propagation in Nonlinear Left-Handed Transmission Line Media,” Applied Physics Letter, Vol. 87, No. 12, 2005, Article ID: 121109. doi:10.1063/1.2056581
- A. B. Kozyrev and D. W. van der Weide, “Trains of Envelope Solitons in Nonlinear Left-Handed Transmission Line Media”, Applied Physics Letter, Vol. 91, No. 25, 2007, Article ID: 254111. doi:10.1063/1.2826282
- A. B. Kozyrev and D. W. van der Weide, “Nonlinear Left-Handed Transmission Line Metamaterials” Journal of Physics D: Applied Physics, Vol. 41, No. 17, 2008, Article ID: 173001.
- J. Ogasawara and K. Narahara, “Experimental Characterization of Left-Handed Transmission Lines with Regularly Spaced Schottky Varactors,” IEICE Electronics Express, Vol. 7, No. 9, 2010, p. 608. doi:10.1587/elex.7.608
- Z. Wang, Y. Feng, B. Zhu, J. Zhao and T. Jiang, “Dark Schrödinger Solitons and Harmonic Generation in LeftHanded Nonlinear Transmission Line”, Journal of Applied Physics, Vol. 107, No. 9, 2010, Article ID: 094907. doi:10.1063/1.3418556
- J. M. Bilbault and P. Marquie, “Energy Localization in a Nonlinear Discrete System,” Physical Review E, Vol. 53, No. 5, 1996, pp. 5403-5408. doi:10.1103/PhysRevE.53.5403
- P. Marquié, J. M. Bilbault and M. Remoissenet, “Observation of Nonlinear Localized Modes in an Electrical Lattice,” Physical Review E, Vol. 51, No. 6, 1995, pp. 6127- 6133. doi:10.1103/PhysRevE.51.6127
- A. B. Togueu Motcheyo, C. Tchawoua, M. Siewe Siewe and J. D. Tchinang Tchameu, “Multisolitons and Stability of Two Hump Solitons of Upper Cutoff Mode in Discrete Electrical Transmission Line,” Physics Letter A, Vol. 375, No. 7, 2011, pp. 1104-1109. doi:10.1016/j.physleta.2011.01.018
- A. Kenfack-Jiotsa and E. Talla-Tebue, “Effect of secondneighbor inductive coupling on the modulational instability in a coupled Line of transmission,” Journal of the Physical Society of Japan, Vol. 80, 2011, Article ID: 034003. doi:10.1143/JPSJ.80.034003
- D. Yemele and F. Kenmogne, “Compact Envelope Dark Solitary Wave in a Discrete Nonlinear Electrical Transmission Line” Physics Letter A, Vol. 373, No. 42, 2009, pp. 3801-3809. doi:10.1016/j.physleta.2009.08.067
- E. Kengne, V. Bozicand, M. Viana and R. Vaillancourt, “Transverse Stability of Solitary Waves Propagating Incoupled Nonlinear Dispersive Transmission Lines,” Physical Review E, Vol. 78, No. 2, 2008, Article ID: 0266036. doi:10.1103/PhysRevE.78.026603
- F. B. Pelap and M. M. Faye, “Higher Order Solitons in an Electrical Lattice,” Journal of the Physical Society of Japan, Vol. 76, No. 7, 2007, Article ID: 074602. doi:10.1143/JPSJ.76.074602
- F. II. Ndzana, A. Mohamadou and T. C. Kofane, “Modulated Waves and Chaotic-Like Behaviours in the Discrete Electrical Transmission Line,” Journal of Applied Physics, Vol. 40, No. 10, 2007, pp. 3254-3262.
- C. G. Lange and A. C. Newell, “A Stability Criterion for Envelope Equations” SIAM Journal of Applied Mathematics, Vol. 27, No. 3, 1974, pp. 441-456. doi:10.1137/0127034
- S. Flach and A. V. Gorbach, “Discrete Breathers,” Physics Reports, Vol. 467, No. 1-3, 2008, pp. 1-116. doi:10.1016/j.physrep.2008.05.002
- M. Sato, S. Yasui, M. Kimura, T. Hikihara and A. J. Sievers, “Management of Localized Energy in Discrete Nonlinear Transmission Lines” Europhysics Letters, Vol. 80, No. 3, 2007, Article ID: 30002. doi:10.1209/0295-5075/80/30002
- L. Q. English, F. Palmero, A. J. Sievers, P. G. Kevrekidis and D. H. Barnak, “Traveling and Stationary Intrinsic Localized Modes and Their Spatial Control in Electrical Lattice,” Physical Review E, Vol. 81, No. 4, 2010, Article ID: 046605. doi:10.1103/PhysRevE.81.046605
- H. Keubou, S. Noubissie and P. Woafo, “Waves Ampli- fication in Nonlinear Transmission Lines Using Negative Nonlinear Resistances,” Journal of the Physical Society of Japan, Vol. 73, No. 5, 2004, pp. 1147-1150. doi:10.1143/JPSJ.73.1147
- J. C. Comte and P. Marquié, “Compact-Like Kink in Real Electrical Reaction—Diffusion Chain,” Chaos, Solitons & Fractals, Vol. 29, No. 2, 2006, pp. 307-312. doi:10.1016/j.chaos.2005.08.212
- H. Willaime, O. Cardoso and P. Tabeling, “Frustration in a Linear Array of Vortices,” Physical Review Letters, Vol. 67, No. 23, 1991, pp. 3247-3250.
- A. Mohamadou, A. K. Jiotsa and T. C. Kofane, “Modulational Instability and Unstable Patterns in the Discrete Complex Cubic Ginzburg-Landau Equation with First and Second Neighbor Couplings,” Physical Reveiw E, Vol. 72, No. 3, 2005, Article ID: 036220.
- A. Minguzzi, P. Vignolo, M. L. Chiofalo and M. P. Tosi, “Hydrodynamic Excitations in a Spin-Polarized Fermi GAS under Harmonic Confinement in One Dimension,” Physical Review A, Vol. 64, No. 3, 2001, Article ID: 033605. doi:10.1103/PhysRevA.64.033605
- F. Kh. Abdullaev and M. Salerno, “Gap-Townes Solitons and Localized Excitations in Low-Dimensional BoseEinstein Condensates in Optical Lattices,” Physical Review A, Vol. 72, No. 3, 2005, Article ID: 033617. doi:10.1103/PhysRevA.72.033617
- K. I. Maruno, Y. Ohta and N. Joshi, “Exact Localized Solutions of Quintic Discrete Nonlinear Schrodinger Equation” Physics Letter A, Vol. 311, No. 2, 2003, pp. 214-220. doi:10.1016/S0375-9601(03)00499-7
- F. II. Ndzanan, A. Mohamadou and T. C. Kofane, “Discrete Lange-Newell Criterion for Dissipative Systems,” Physical Review E, Vol. 79, No. 5, 2009, Article ID: 056611. doi:10.1103/PhysRevE.79.056611
- A. Khare, S. V. Dmitriev and A. Saxena, “Exact Moving and Stationary Solutions of a Generalized Discrete Nonlinear Schrödinger Equation,” Journal of Physics A, Vol. 40, No. 37, 2007, pp. 11301-11317.
- A. Khare, S. V. Dmitriev and A. Saxena, “Exact static Solutions of a Generalized Discrete φ4 Model Including Short-Periodic Solutions” Journal of Physics A, Vol. 42, No. 14, 2009, Article ID: 145204. doi:10.1088/1751-8113/42/14/145204
- R. Stearrett and L. Q. English, “Experimental Generation of Intrinsic Localized Modes in a Discrete Electrical Transmission Line,” Journal of Physics D, Vol. 40, No. 17, 2007, pp. 5394-539. doi:10.1088/0022-3727/40/17/058
- G. M. Chechin and V. P. Sakhenenko, “Interactions between Normal Modes in Nonlinear Dynamical System with Discrete Symmetry. Exact Results,” Physica D, Vol. 117, No. 1-4, 1998, pp. 43-76. doi:10.1016/S0167-2789(98)80012-2
- G. M. Chechin and K. G. Zhukov, “Stability Analysis of Dynamical Regimes in Nonlinear Systems with Discrete Symmetries,” Physical Review E, Vol. 73, No. 3, 2006, Article ID: 036216.
- G. M. Chechin, N. V. Novikora and A. A. Abramenko, “Bushes of Vibrational Modes for Fermi-Pasta-Ulam Chains”, Physica D, Vol. 166, No. 3-4, 2002, pp. 208-238. doi:10.1016/S0167-2789(02)00430-X
Appendix
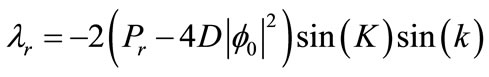
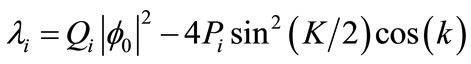
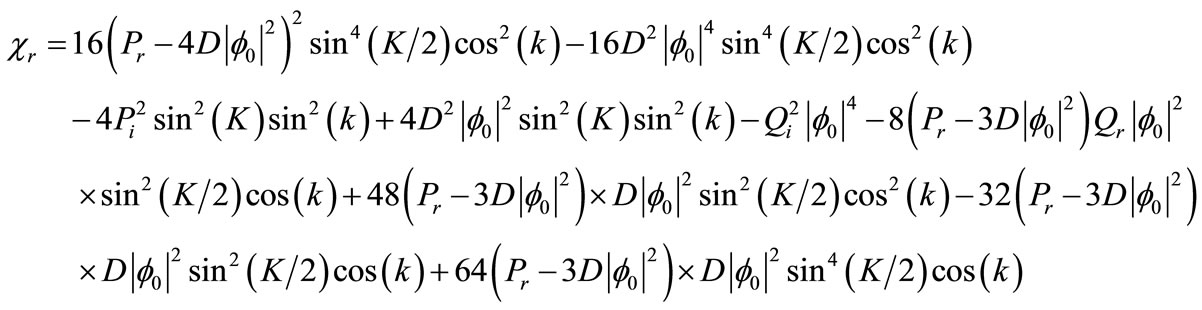
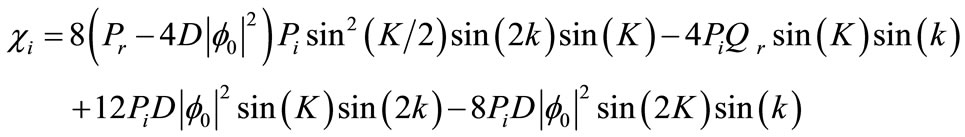
NOTES
*Corresponding author.

