Journal of Modern Physics
Vol.3 No.4(2012), Article ID:18897,8 pages DOI:10.4236/jmp.2012.34043
Novel Superpotentials for Supersymmetric Quantum Mechanics: A New Mathematical Investigation and Study
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani62@yahoo.com
Received November 11, 2011; revised December 30, 2011; accepted January 16, 2012
Keywords: Superpotentials; Supersymmetric; Quantum Mechanics; Schrödinger Equation; Operator Method; Coulomb Superpotential; Klein-Gordon Energies
ABSTRACT
It is inferred from the articles on supersymmetric quantum mechanics that a few number of potentials with accurate solutions have been hitherto introduced for the Schrödinger equation. Most of those potentials possess a variable parameter and a constant parameter and some of them have two constant parameters and two variable parameters to achieve various wave functions and energy levels through the operator method. These potentials are derived from the functions called superpotentials. In this paper, first, we start with a general superpotential with two constant parameters and four variable parameters; however in the calculations, we are actually required to apply constraints resulting in three different types of superpotential having characteristics such as: 1) For specific values of parameters, they are transformed into some of previously known superpotentials that this result indicates their correctness. 2) Since such superpotentials generating previous superpotentials have not been heretofore proposed, they are novel. 3) Moreover, the claim that all the previously known superpotentials are subsets of Coulomb superpotential, three-dimensional oscillating superpotential, and transferred oscillating superpotential is new. 4) Each category of three superpotentials above creates potentials whose Klein-Gordon energies have equal distances, but the constraint applied for this purpose reduces the number of variable parameters.
1. Introduction
In this work, referring to the articles about supersymmetric quantum mechanics (SUSY QM) or about potentials having accurate solution, we utilize some of them such as Cooper’s review article published in 1995 [1] that through assuming:
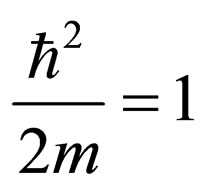 (1)
(1)
and by means of superpotential 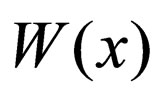 and its derivative
and its derivative , two self-consistent potentials
, two self-consistent potentials 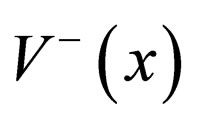 and
and 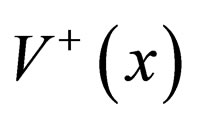 are obtained as follows:
are obtained as follows:
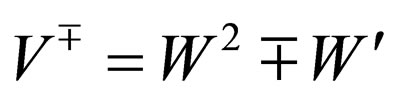 (2)
(2)
If for all the 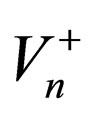 and
and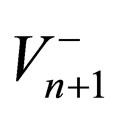 , there are x-independent
, there are x-independent 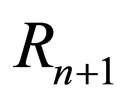 s satisfying the following shape-invariance equation:
s satisfying the following shape-invariance equation:
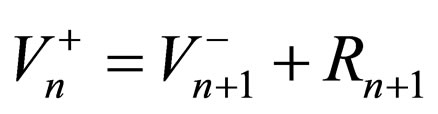 (3)
(3)
The energy levels are obtained through the following important equation:
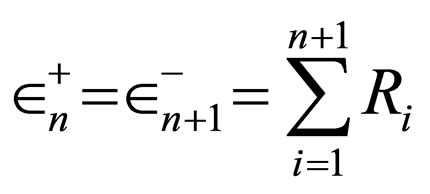 (4)
(4)
On the other hand, assuming that 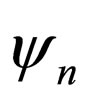 is the wave function of n-th level and
is the wave function of n-th level and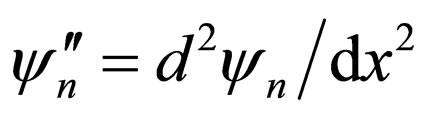 , the Schrö- dinger equation for this level is as follows:
, the Schrö- dinger equation for this level is as follows:
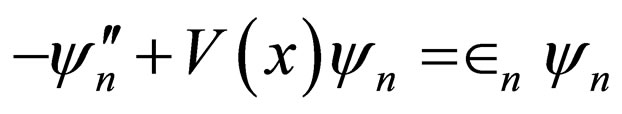 (5)
(5)
If the ground energy level for the potential 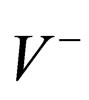 is formulated by the known function
is formulated by the known function 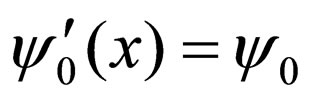 on zero (
on zero (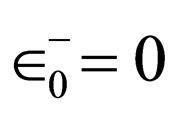 ), by considering Equation (5) we acquire:
), by considering Equation (5) we acquire:
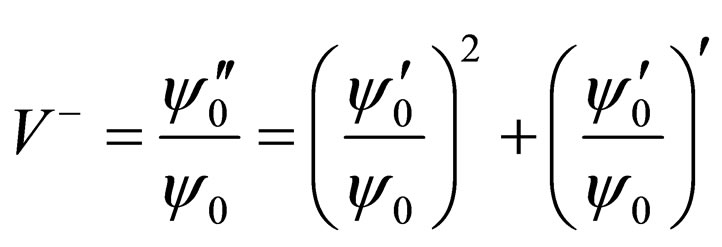 (6)
(6)
However, by comparing Equation (6) with Equation (2), the superpotential W is:
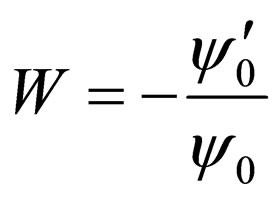 (7)
(7)
Conversely, if the superpotential 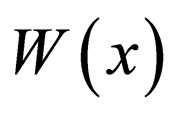 is a characteristic function,
is a characteristic function, 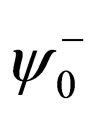 can be:
can be:
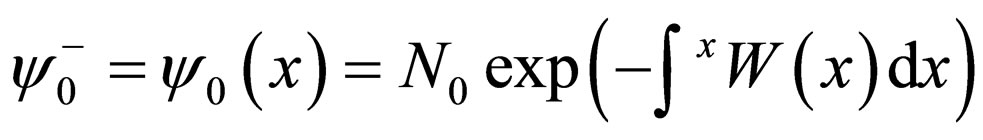 (8)
(8)
where 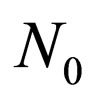 is the normalizing factor.
is the normalizing factor.
Afterwards, through the operator method and by virtue of the raising operator below:
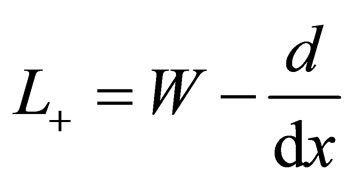 (9)
(9)
other energy levels’ characteristic functions are as follows:
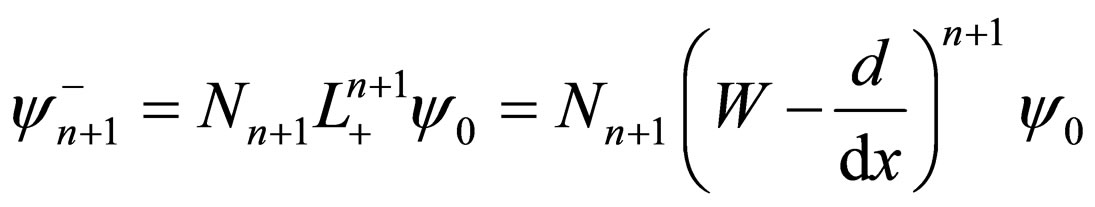 (10)
(10)
For such potentials, since the Schrödinger equation’s 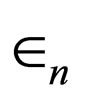 s and
s and 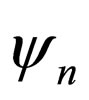 s can be accurately obtained by Equations (4), (8), and (10), they are termed potentials with accurate solution.
s can be accurately obtained by Equations (4), (8), and (10), they are termed potentials with accurate solution.
Through this method, a few numbers of potentials have been hitherto discovered. Twelve cases of these potentials are well known for which 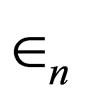 s and
s and 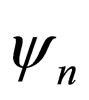 s are accurately computed. After the publication of Cooper’s review article in 1995 [1], although the scientists have sought to propose newer potentials using the abovementioned method for many years, any new or important potential has not been heretofore introduced.
s are accurately computed. After the publication of Cooper’s review article in 1995 [1], although the scientists have sought to propose newer potentials using the abovementioned method for many years, any new or important potential has not been heretofore introduced.
2. The Classification of Well-Known Superpotentials
With regard to the supersymmetric quantum mechanics, twelve superpotentials [1-47] have been hitherto proposed whose Schrödinger equation and its resulting potentials possess accurate solution.
In terms of parameters’ type, the well-known superpotentials are divided into three main categories.
2.1. A Superpotential with Two Constant Parameters A and B
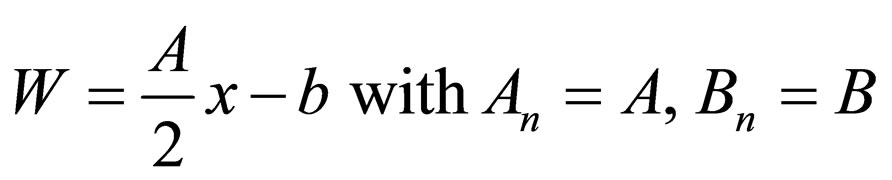 (11)
(11)
is the generator of transferred oscillating potential with the energies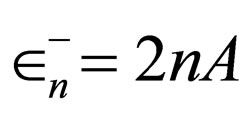 .
.
2.2. Superpotentials with a Variable Parameter A and a Constant Parameter B
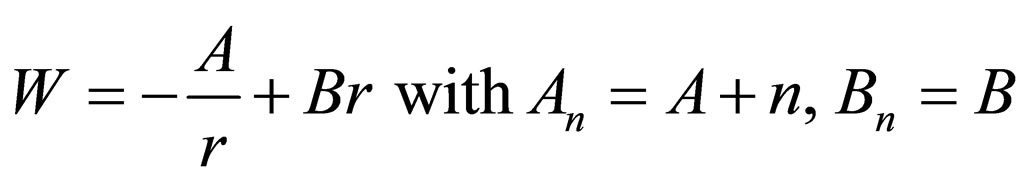 (12)
(12)
is the generator of three-dimensional oscillating potential with the energies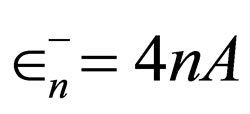 .
.
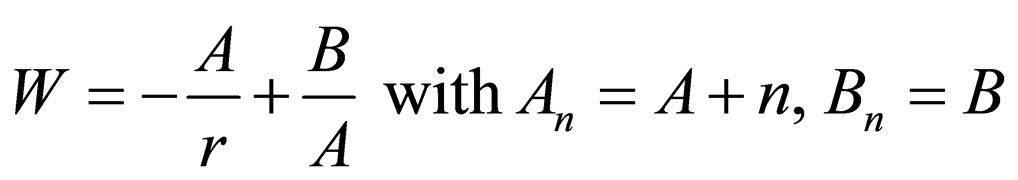 (13)
(13)
is the generator of Coulomb potential with the energies
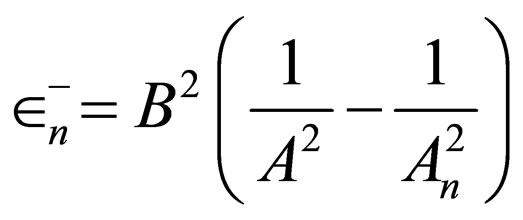 .
.
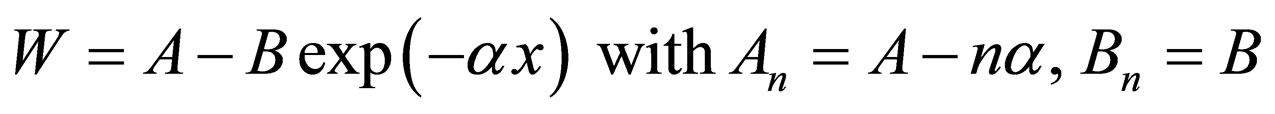 (14)
(14)
is the generator of Morse potential with the energies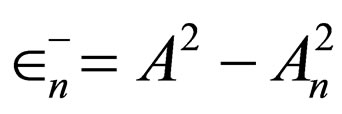 .
.
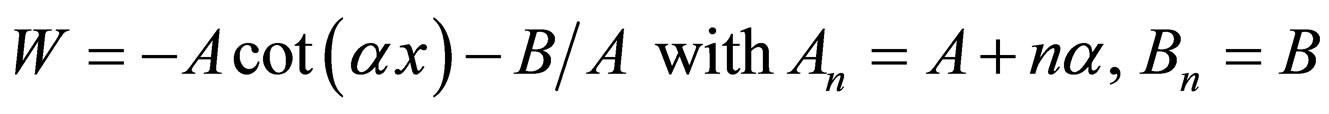 (15)
(15)
is the generator of Rosen-Morse I potential with the energies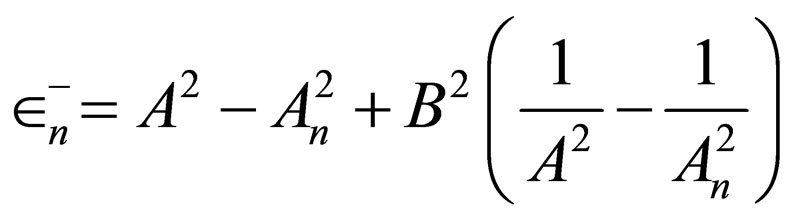 .
.
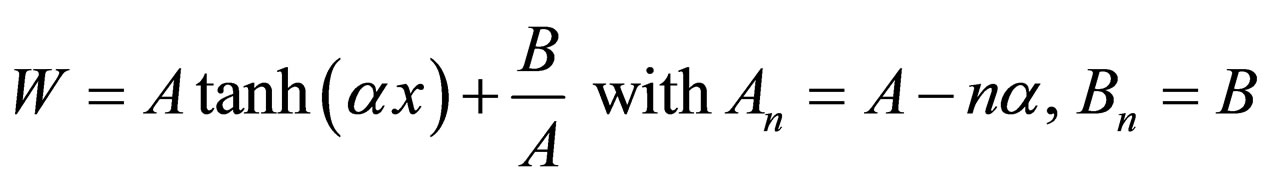 (16)
(16)
is the generator of Rosen-Morse II potential with the energies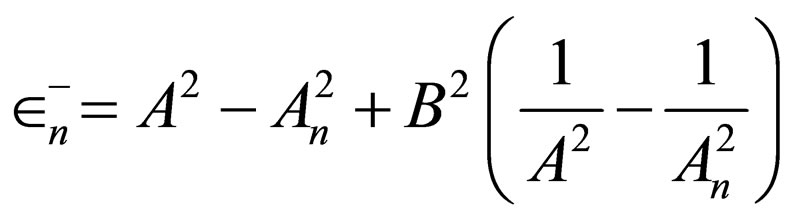 .
.
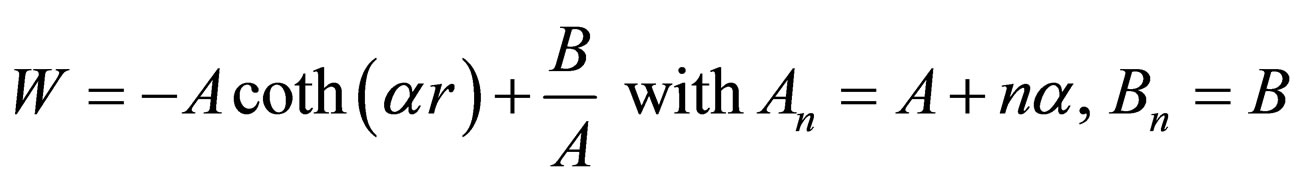 (17)
(17)
is the generator of Eckart potential with the energies
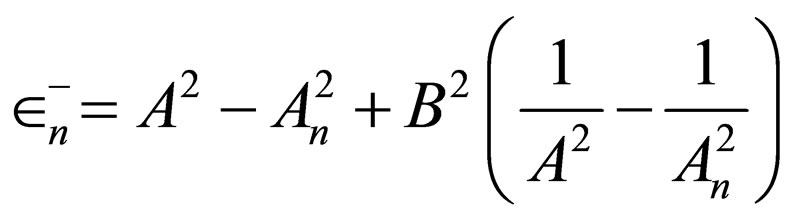 .
.
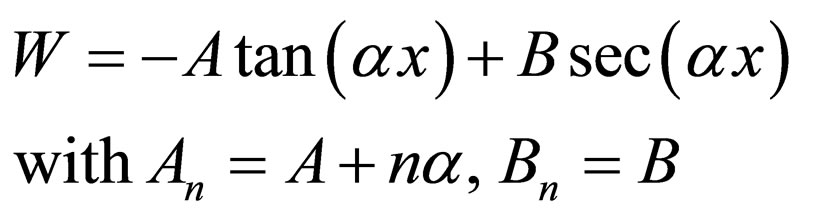 (18)
(18)
is the generator of Scarf I potential with the energies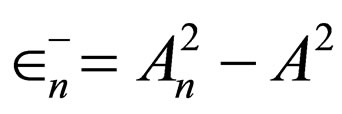 .
.
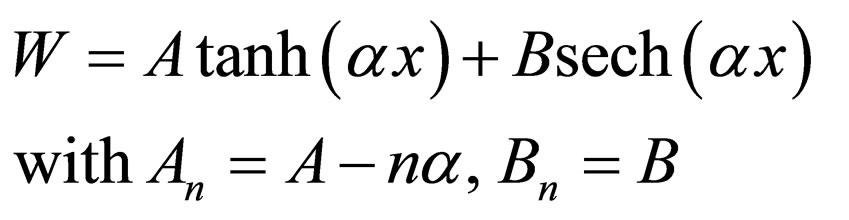 (19)
(19)
is the generator of Scarf II potential with the energies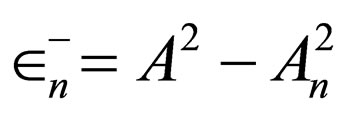 .
.
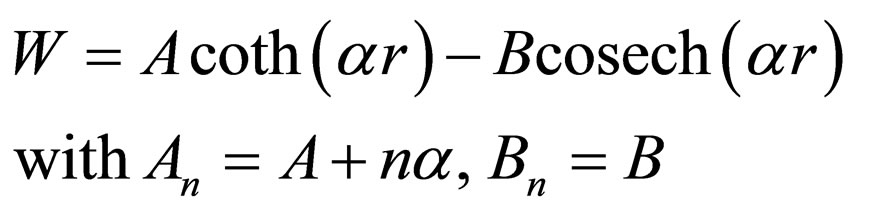 (20)
(20)
is the generator of generalized Pöschl-Teller potential with the energies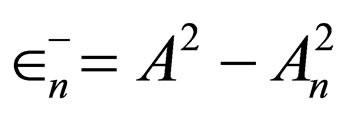 .
.
2.3. Superpotentials with Two Variable Parameters A and B
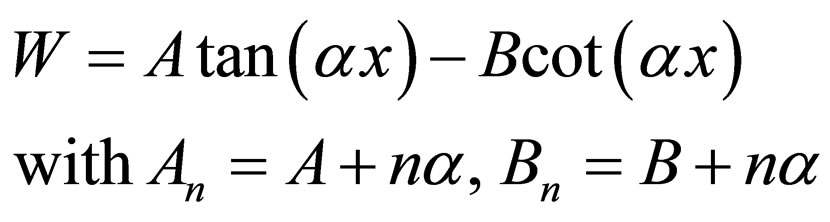 (21)
(21)
is the generator of Pöschl-Teller I potential with the energies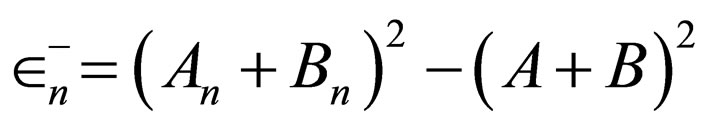 .
.
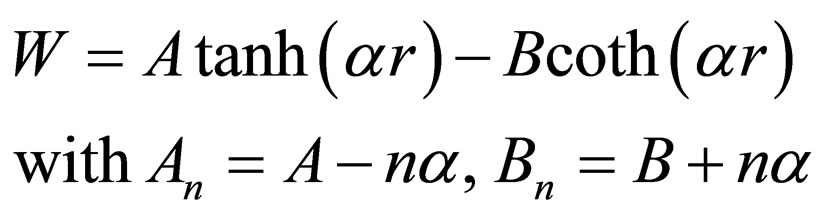 (22)
(22)
is the generator of Pöschl-Teller II potential with the energies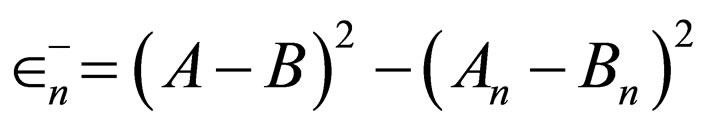 .
.
3. Creating the Intended Superpotentials
Considering the form of functions W in Equations (14) to
(22), and through utilizing two constant parameters β and γ, and four general parameters C, D, F, and G, the following general superpotential is considered:
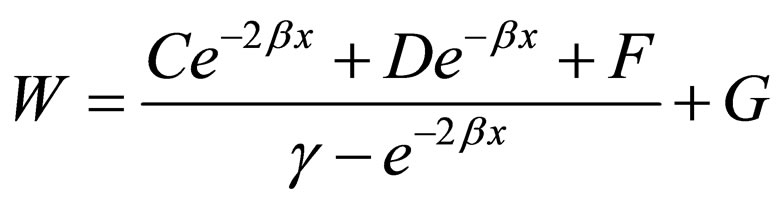 (23)
(23)
By applying the shape-invariance condition of Equation (3) to the above superpotential, a number of constraint equations of parameters C, D, F, G, 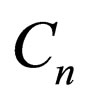 ,
, 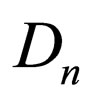 ,
, 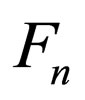 , and
, and 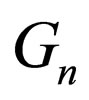 are found whose general solutions are not simply possible; however, if the special cases are considered, three cases of them lead to the following three categories.
are found whose general solutions are not simply possible; however, if the special cases are considered, three cases of them lead to the following three categories.
3.1. A Superpotential with a Variable Parameter
For the special case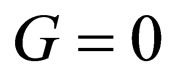 , the constraints resulting from Equation (3) for the first step (
, the constraints resulting from Equation (3) for the first step (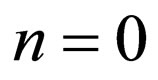 ) are as follows:
) are as follows:
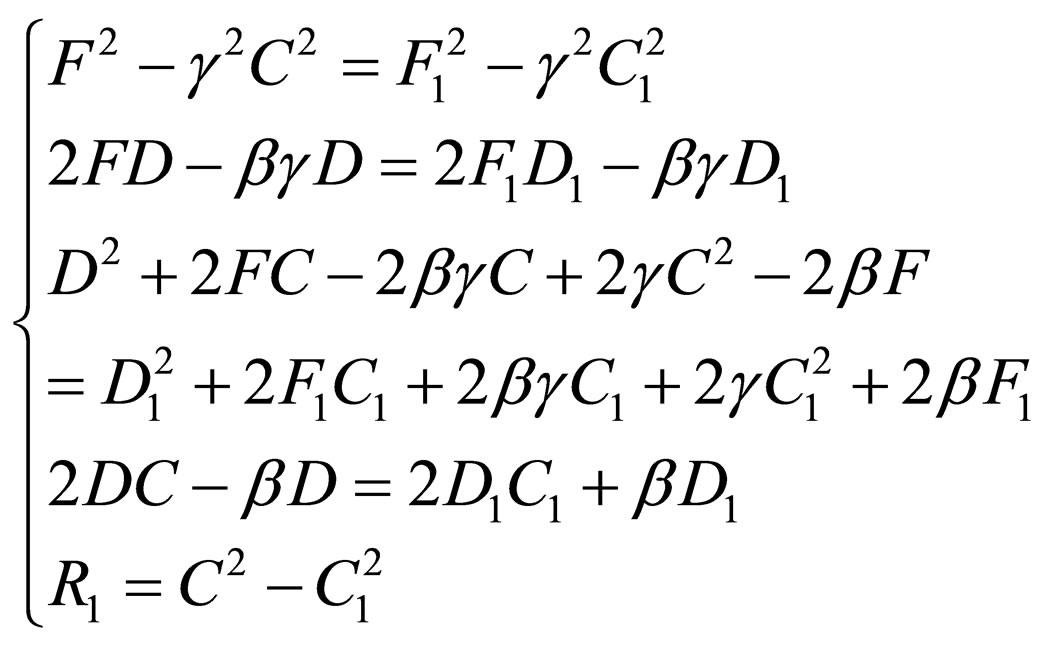 (24)
(24)
The designation below is appropriate for the above equations:
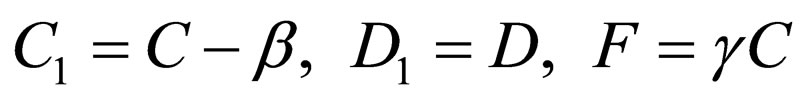 (25)
(25)
It means that our intended superpotential for the n-th level in the state 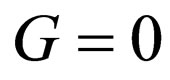 should be written as the following form:
should be written as the following form:
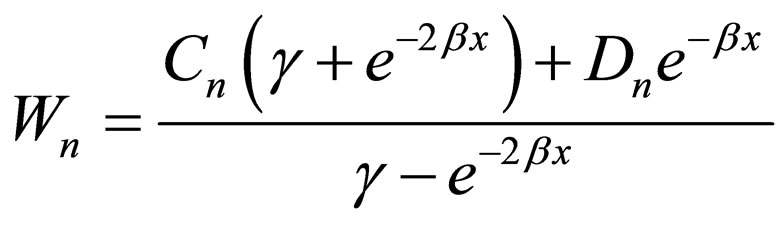 (26)
(26)
and the necessary equations for the shape invariance between n-th level and n + 1-th level are as follows:
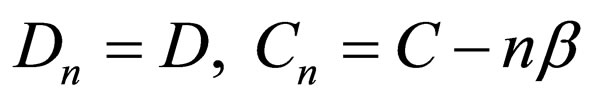 (27)
(27)
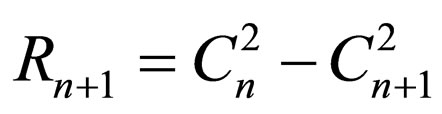 (28)
(28)
Then, through exploiting Equations (4) and (28), the energy levels are:
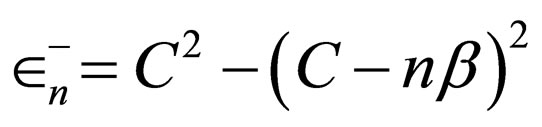 (29)
(29)
By means of these two transforms 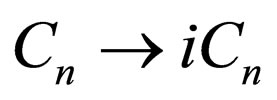 and
and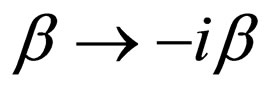 , the four equations above are transformed into the forms below:
, the four equations above are transformed into the forms below:
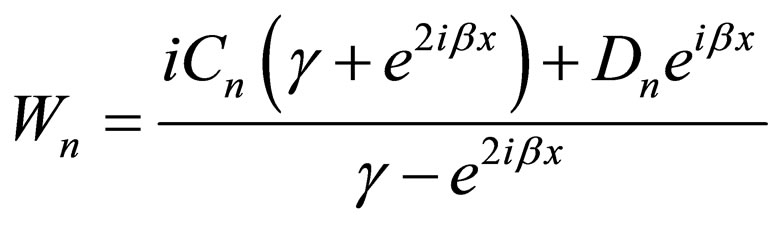 (30)
(30)
 (31)
(31)
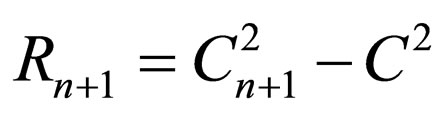 (32)
(32)
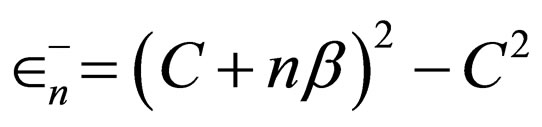 (33)
(33)
In special cases of Equations (26), (29), (30), and (33), a number of previously known superpotentials and their respective energies can be achieved of which the main ones are:
1) Selecting 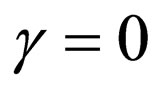 from Equation (26) results in
from Equation (26) results in 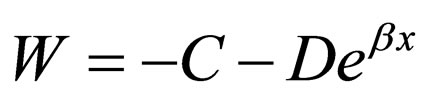 which is the Morse superpotential (Equation (14)) with the energies
which is the Morse superpotential (Equation (14)) with the energies 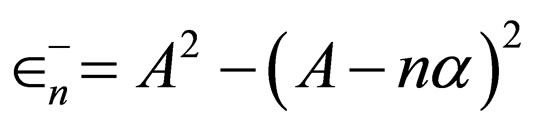 by assuming
by assuming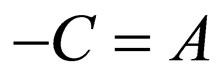 ,
,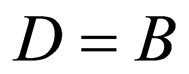 , and
, and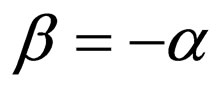 .
.
2) Selecting 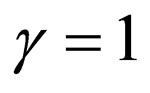 from Equation (26) results in
from Equation (26) results in 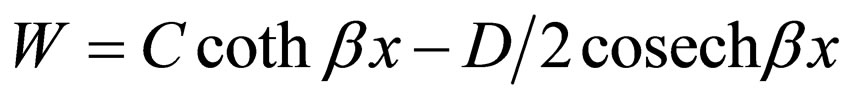 which is the generalized Pöschl-Teller superpotential (Equation (20)) with the energies
which is the generalized Pöschl-Teller superpotential (Equation (20)) with the energies 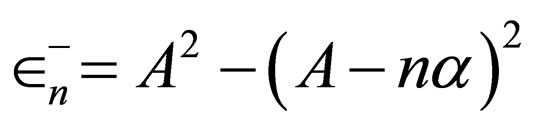 by assuming
by assuming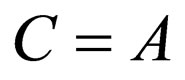 ,
, 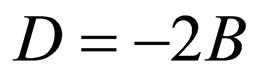 , and
, and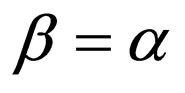 .
.
3) Selecting 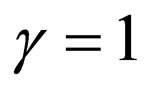 from Equation (26) results in
from Equation (26) results in 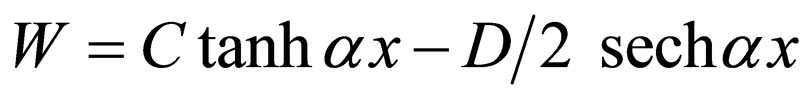 which is the Scarf II superpotential (Equation (19)) with the energies
which is the Scarf II superpotential (Equation (19)) with the energies 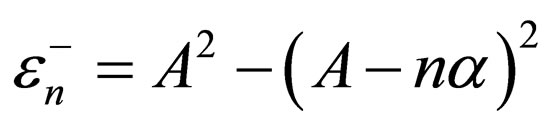 by assuming
by assuming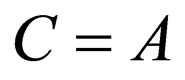 ,
, 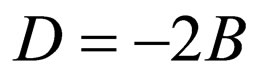 , and
, and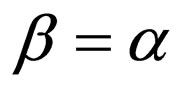 .
.
4) Selecting 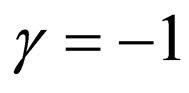 from Equation (30) results in
from Equation (30) results in 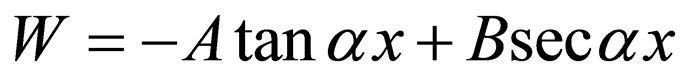 which is the Scarf I superpotential (Equation (18)) with the energies of Equation (33)
which is the Scarf I superpotential (Equation (18)) with the energies of Equation (33) 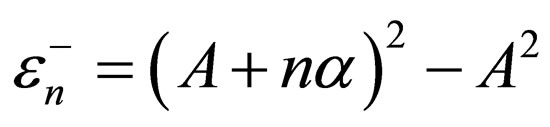 by assuming
by assuming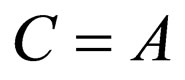 ,
, 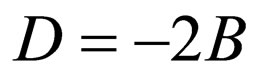 , and
, and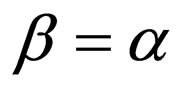 .
.
5) Selecting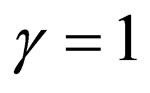 ,
, 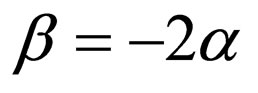 ,
, 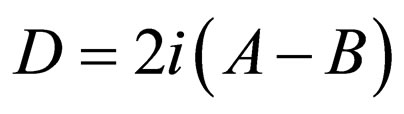 , and
, and  , Equation (30) is transformed into
, Equation (30) is transformed into 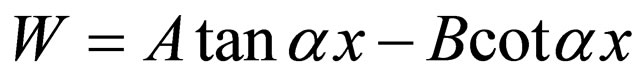 which is the Pöschl-Teller I superpotential; considering Equation (31),
which is the Pöschl-Teller I superpotential; considering Equation (31), 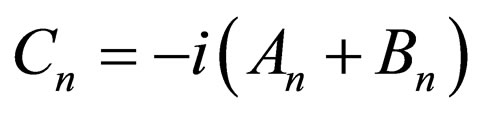 , and
, and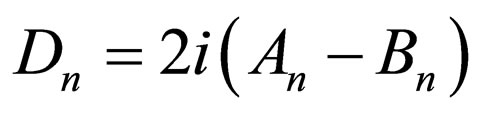 , there should be
, there should be 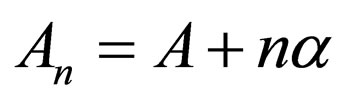 and
and ; the energies of Pöschl-Teller I (
; the energies of Pöschl-Teller I (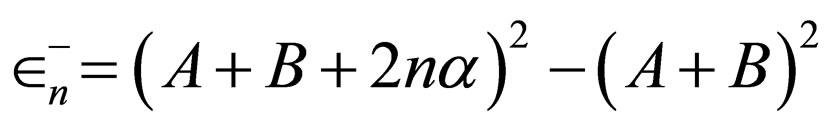 ) are derived from Equation (33).
) are derived from Equation (33).
6) Selecting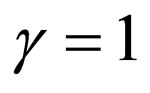 ,
, 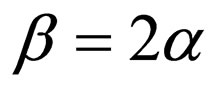 ,
, 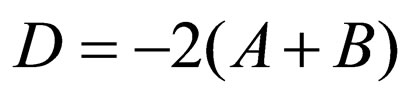 , and
, and 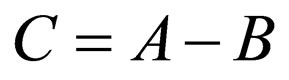 , Equation (26) is transformed into
, Equation (26) is transformed into 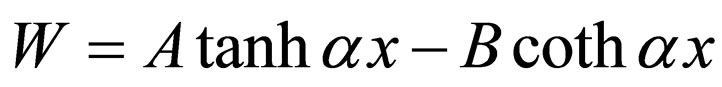 which is the Pöschl-Teller II superpotential; considering Equation (27),
which is the Pöschl-Teller II superpotential; considering Equation (27), 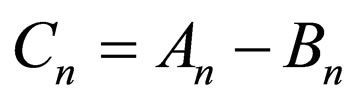 , and
, and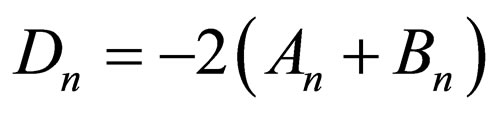 , there should be
, there should be 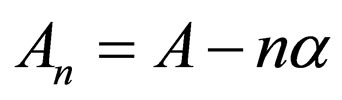 and
and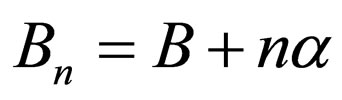 ; the energies of Pöschl-Teller II (
; the energies of Pöschl-Teller II (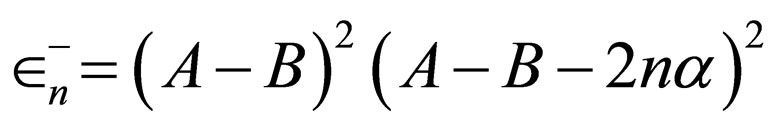 ) are derived from Equation (29).
) are derived from Equation (29).
3.2. A Superpotential with Two Variable Parameters
For the special case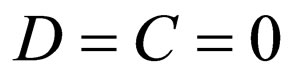 , through assuming
, through assuming 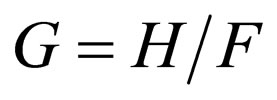 , Equation (23) is transformed into the following form:
, Equation (23) is transformed into the following form:
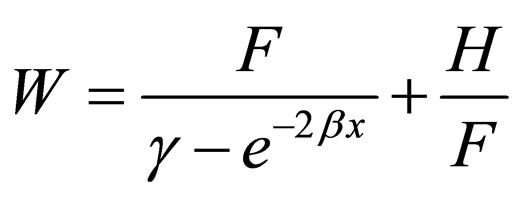 (34)
(34)
for which, through applying the shape-invariance condition of Equation (3) for n = 0, it becomes necessary that:
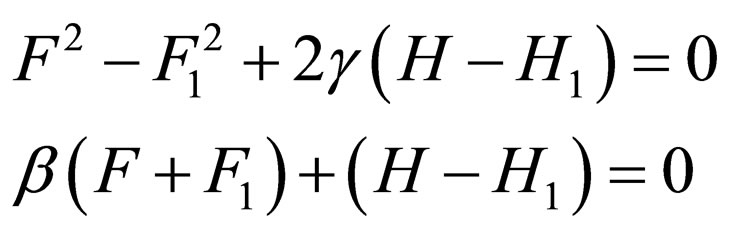 (35)
(35)
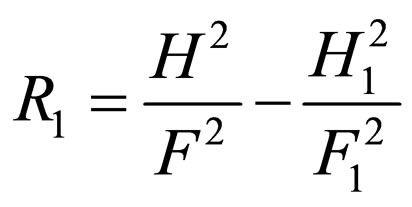 (36)
(36)
After removing 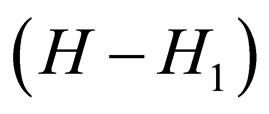 from the functions of Equation (35), it can be written as follows:
from the functions of Equation (35), it can be written as follows:
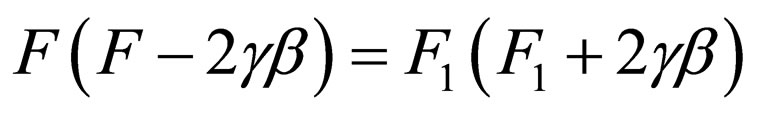 (37)
(37)
in which the following solution satisfies:
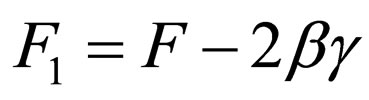 (38)
(38)
By inputting Equation (38) to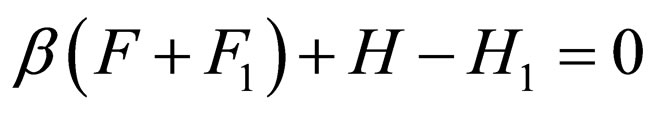 :
:
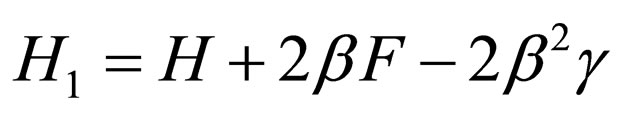 (39)
(39)
Also, by applying the shape-invariance condition of Equation (3) for the general level n, we obtain:
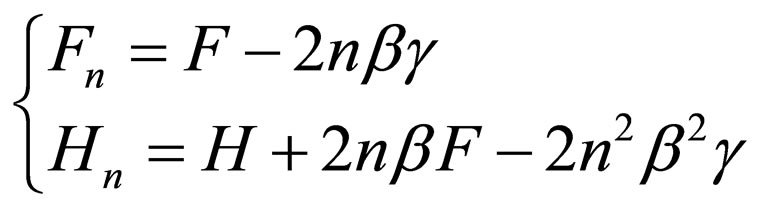 (40)
(40)
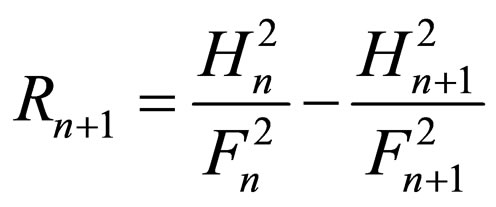 (41)
(41)
Then, through Equations (4), (40), and (41), the energy levels are achieved as follows:
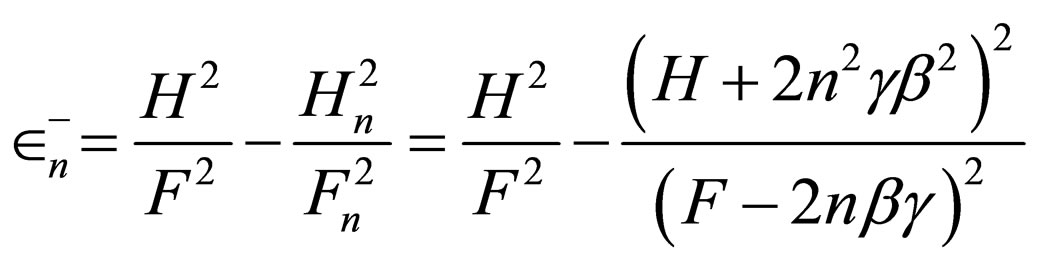 (42)
(42)
Also, through transforming 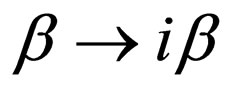 and
and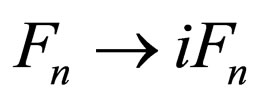 , Equations (34), (40), and (42) are transformed into the following forms:
, Equations (34), (40), and (42) are transformed into the following forms:
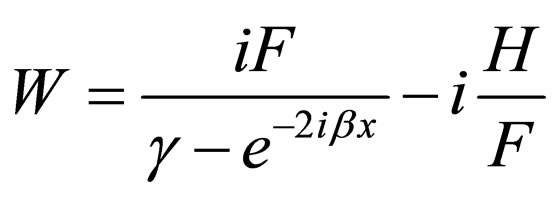 (43)
(43)
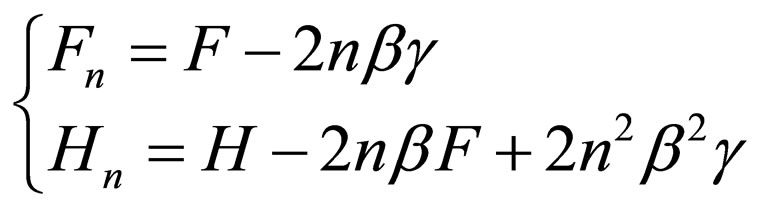 (44)
(44)
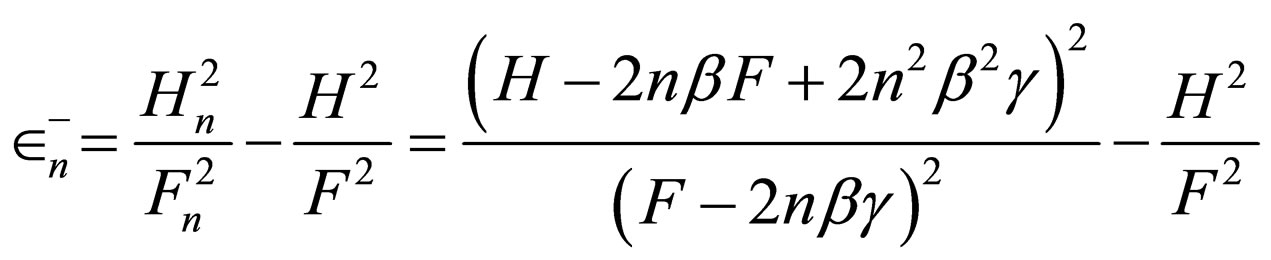 (45)
(45)
For the special case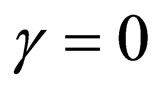 , in which the superpotential of Equation (34) is transformed into
, in which the superpotential of Equation (34) is transformed into 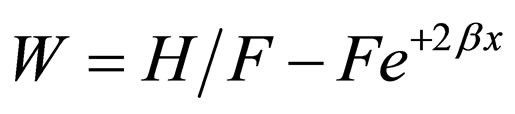 which is the Morse superpotential
which is the Morse superpotential 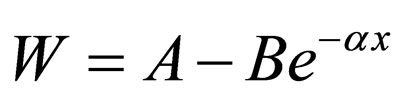 by assuming
by assuming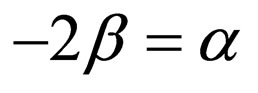 ,
, 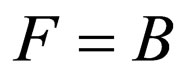 , and
, and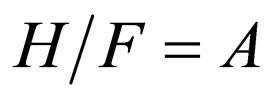 ; the transforms
; the transforms 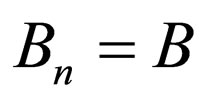 and
and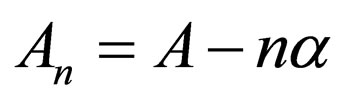 , and the energies of Morse superpotential of Equation (14),
, and the energies of Morse superpotential of Equation (14), 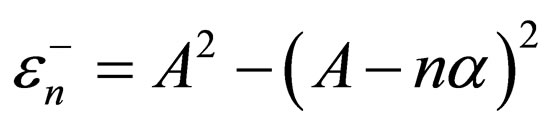 , are obtained through Equations (40) and (42). Furthermore, with
, are obtained through Equations (40) and (42). Furthermore, with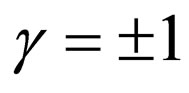 , for the special cases
, for the special cases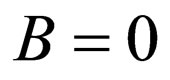 , the superpotentials of Scarf II, Rosen-Morse I and II, and Pöschl-Teller I and II result from the superpotentials of Equations (34) and (43). This indicates the results’ correctness.
, the superpotentials of Scarf II, Rosen-Morse I and II, and Pöschl-Teller I and II result from the superpotentials of Equations (34) and (43). This indicates the results’ correctness.
3.3. A Superpotential with Three Variable Parameters
For the special case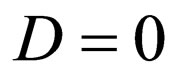 , in which Equation (23) is transformed into the form below:
, in which Equation (23) is transformed into the form below:
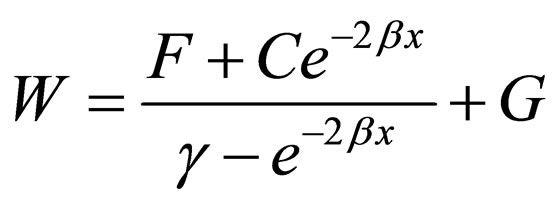 (46)
(46)
through applying the shape-invariance condition of Equation (3) for the first step (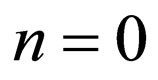 ), the following constraints should be necessarily established:
), the following constraints should be necessarily established:
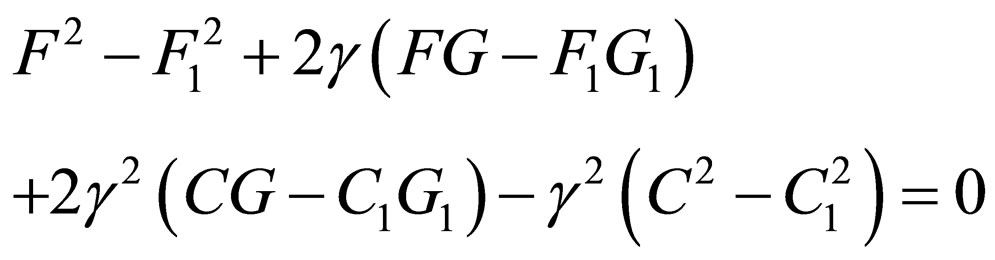 (47)
(47)
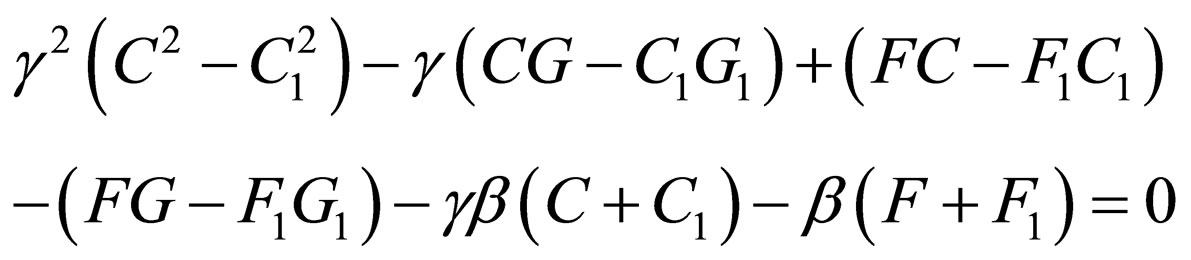 (48)
(48)
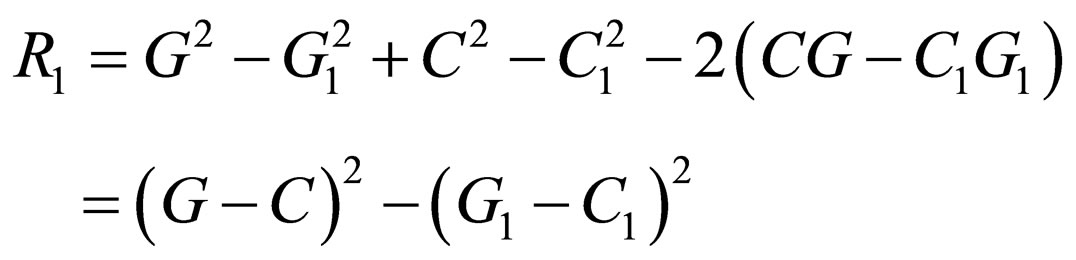 (49)
(49)
Now, by achieving 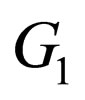 through Equations (47) and (48), and equalizing them, we obtain the result below:
through Equations (47) and (48), and equalizing them, we obtain the result below:
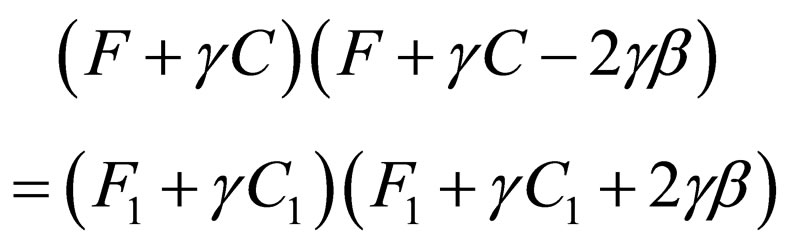 (50)
(50)
in which the following equations fulfill:
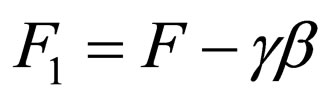 (51)
(51)
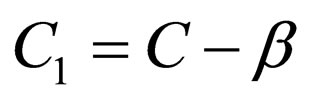 (52)
(52)
Through inputting Equations (51) and (52) to Equation (47), 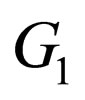 is acquired as follows:
is acquired as follows:
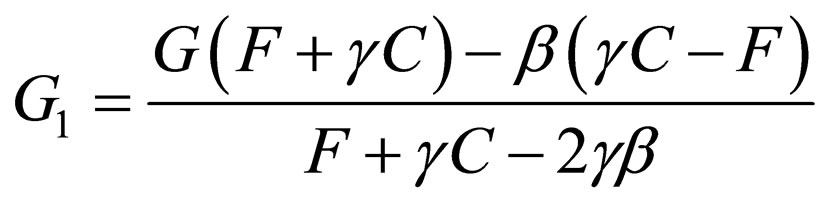 (53)
(53)
In the second step, by applying the shape-invariance condition of Equation (3), the following functions are obtained:
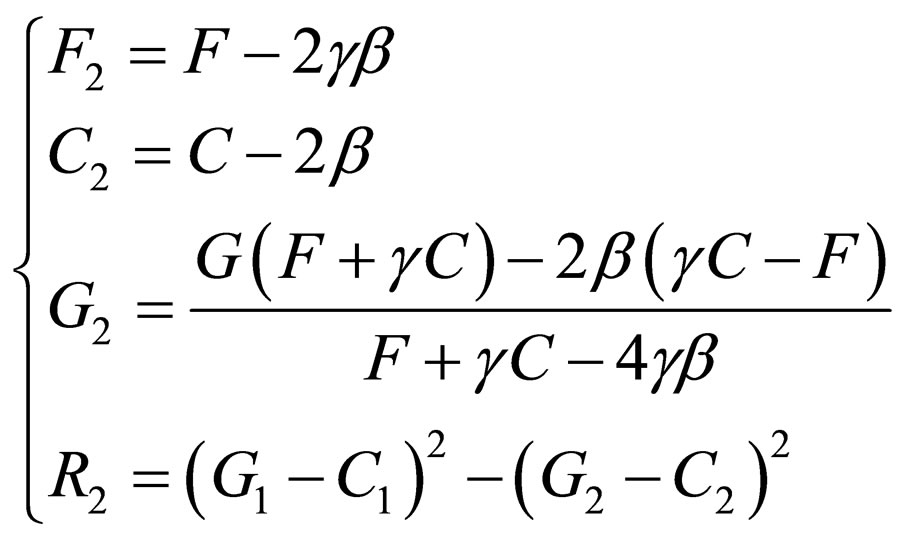 (54)
(54)
Subsequently, in the n-th step, we will have:
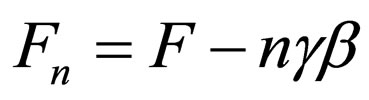 (55)
(55)
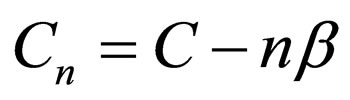 (56)
(56)
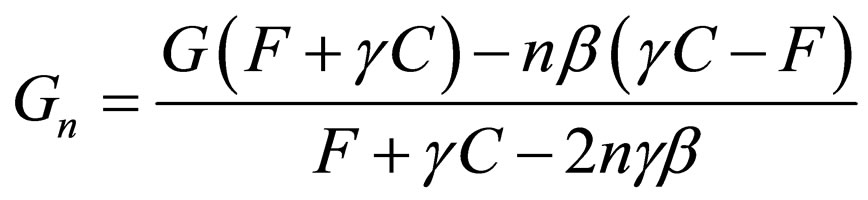 (57)
(57)
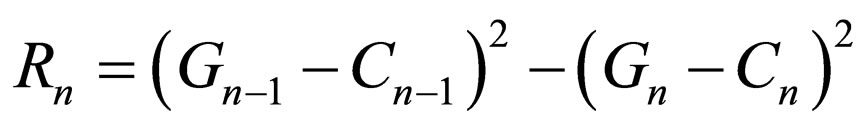 (58)
(58)
Through utilizing Equation (4), its energies are as follows:
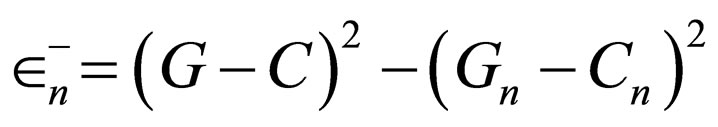 (59)
(59)
By transforming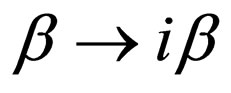 ,
,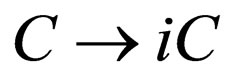 ,
, , and
, and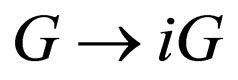 , Equations (46) and (59) are converted into the forms below:
, Equations (46) and (59) are converted into the forms below:
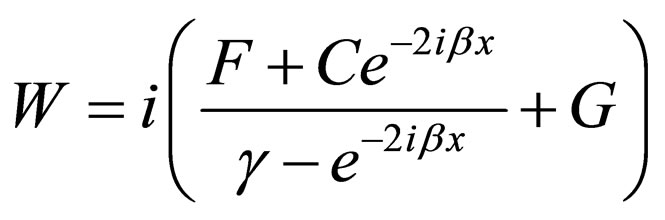 (60)
(60)
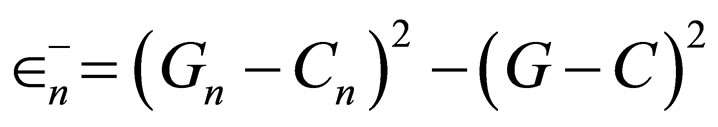 (61)
(61)
But, Equations (55)-(57) are not changed.
Here again, to insure the above equations’ accuracy, some special cases of Equations (46) and (60) are obtained in the following steps:
1) For the special case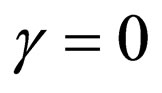 , Equation (46) is converted to
, Equation (46) is converted to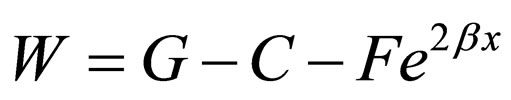 , and Equations (55)-(57) are respectively transformed into Fn = F,
, and Equations (55)-(57) are respectively transformed into Fn = F, 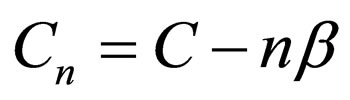 , and
, and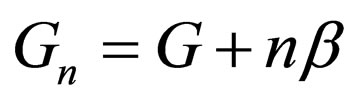 ; by assuming
; by assuming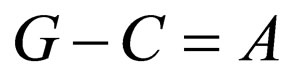 ,
, 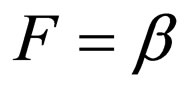 , and
, and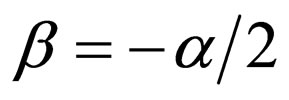 , the equations of Morse superpotential (
, the equations of Morse superpotential (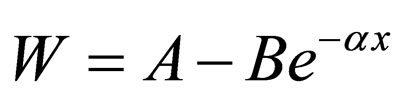 ,
,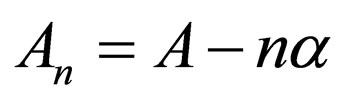 , and
, and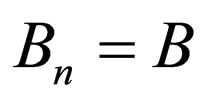 ) are acquired; the Morse energies,
) are acquired; the Morse energies, 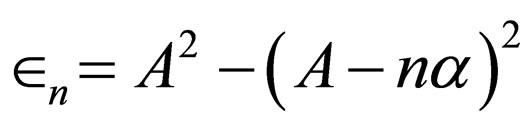 , are derived from Equation (59).
, are derived from Equation (59).
2) For the special case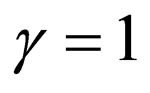 , in which
, in which 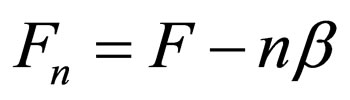 and
and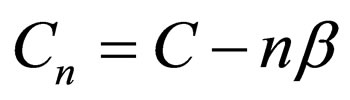 , it can be assumed that
, it can be assumed that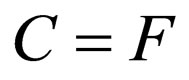 . Then by assuming
. Then by assuming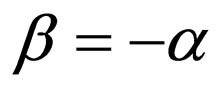 , Equation (46) is transformed into
, Equation (46) is transformed into 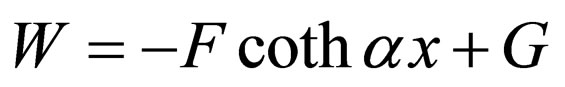 where
where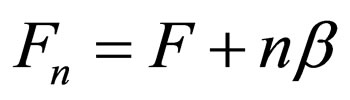 and
and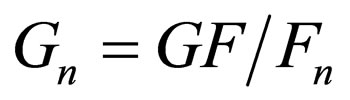 ; by assuming
; by assuming 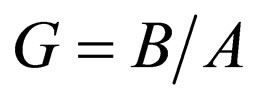 and
and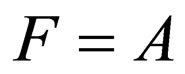 , the Eckart superpotential
, the Eckart superpotential 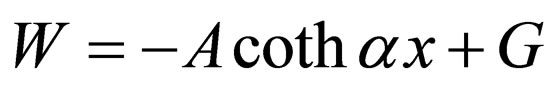 is achieved. The Eckart energies,
is achieved. The Eckart energies,
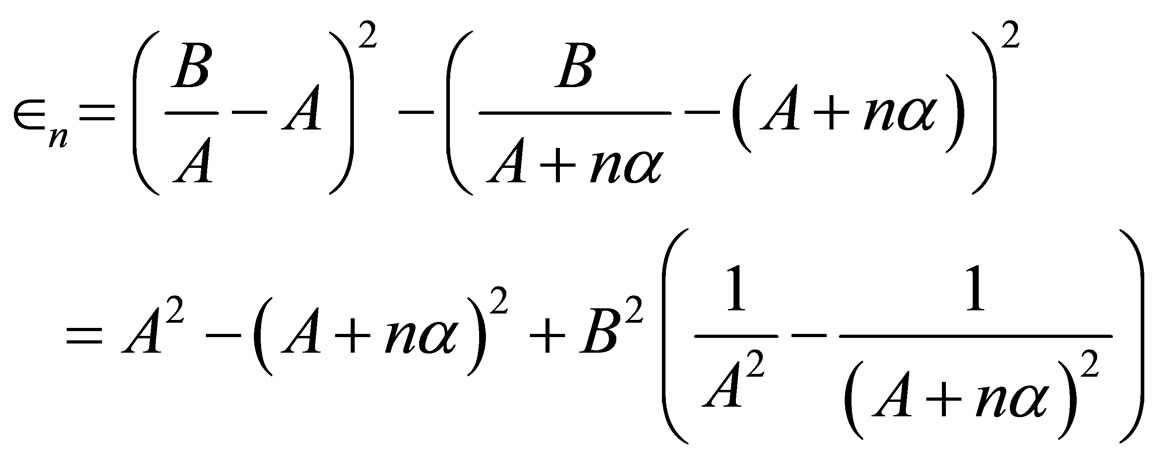
are obtained through Equation (59).
3) For the special case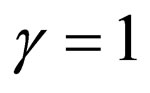 , by assuming
, by assuming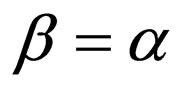 ,
, 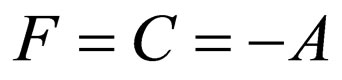 , and
, and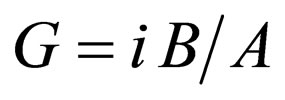 , Equation (60) is transformed into the Rosen-Morse I superpotential (
, Equation (60) is transformed into the Rosen-Morse I superpotential (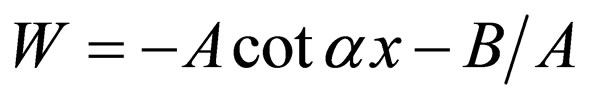 ) and the energies of Equation (61) are converted to those of Rosen-Morse I
) and the energies of Equation (61) are converted to those of Rosen-Morse I
(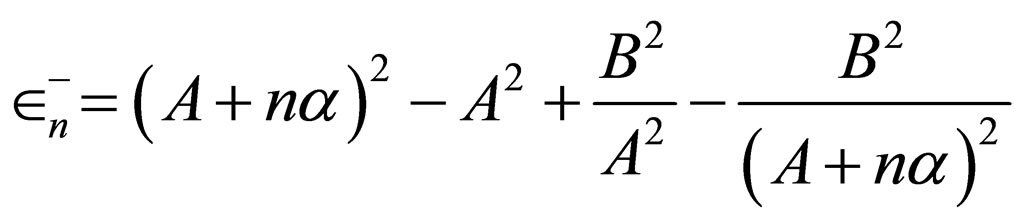 ).
).
4) For the special case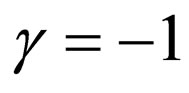 , by assuming
, by assuming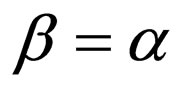 ,
,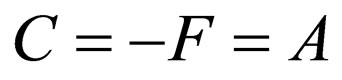 , and
, and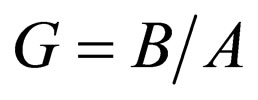 , Equation (46) is transformed into the Rosen-Morse II superpotential (
, Equation (46) is transformed into the Rosen-Morse II superpotential (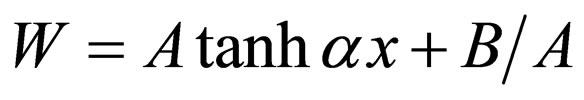 ) and the energies of Equation (59) are converted to those of Rosen-Morse II
) and the energies of Equation (59) are converted to those of Rosen-Morse II
(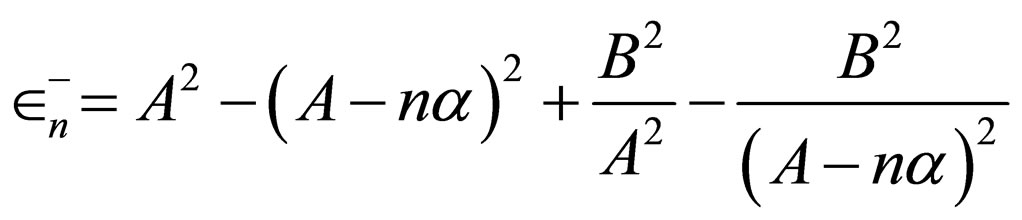 ).
).
4. The Application in Fundamental Particles
In the articles on the quarkonium spectroscopy using the Klein-Gordon equation [48-52] and the coherent state of no-spin relativistic particle [53-57], some applications of Schrödinger equation’s energies are employed to obtain relativistic particles’ energy spectra, the importance of equally-spaced Klein-Gordon relativistic equation’s energy levels is investigated, and the characteristic values of Klein-Gordon equation 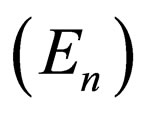 according to the characteristic values of Schrödinger equation
according to the characteristic values of Schrödinger equation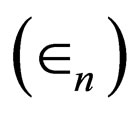 are achieved as follows:
are achieved as follows:
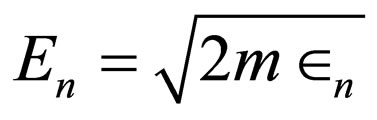 (62)
(62)
where m is the particle’s rest mass.
On the other hand, if the energies of Schrödinger equation for a potential like 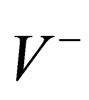 are
are 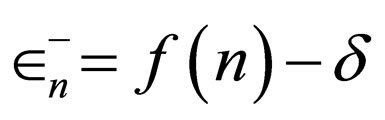 where δ is an n-independent constant, the energies of Schrödinger equation for the potential
where δ is an n-independent constant, the energies of Schrödinger equation for the potential 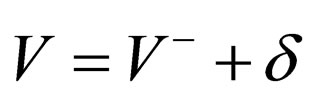 is
is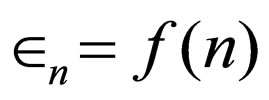 ; based on Equation (62), the energies of Klein-Gordon equation for the potential
; based on Equation (62), the energies of Klein-Gordon equation for the potential 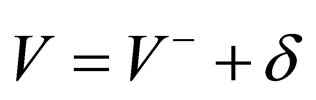 should be obtained through the following equation:
should be obtained through the following equation:
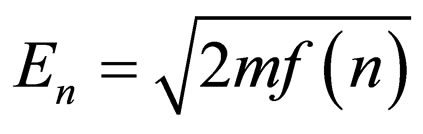 (63)
(63)
Therefore, if 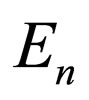 is obtained as a first-order function of n, the Klein-Gordon energy levels will have equal distances. In this section, we utilize some of energies (
is obtained as a first-order function of n, the Klein-Gordon energy levels will have equal distances. In this section, we utilize some of energies (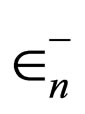 ) resulting from the superpotentials achieved in the Sections 3.1, 3.2, and 3.3 as follows:
) resulting from the superpotentials achieved in the Sections 3.1, 3.2, and 3.3 as follows:
1) Regarding Equations (30) and (33), if through using:
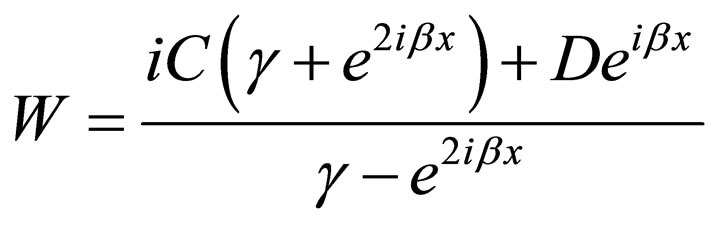 (64)
(64)
we form the potential below:
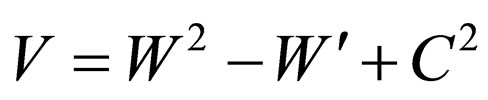 (65)
(65)
its 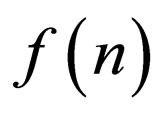 will be as the following form:
will be as the following form:
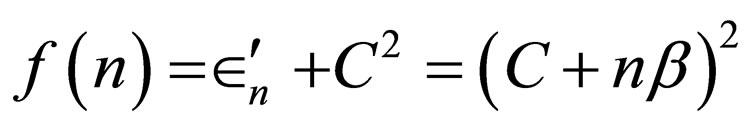 (66)
(66)
Subsequently, by exploiting Equations (63) and (66), the Klein-Gordon equation’s energies include:
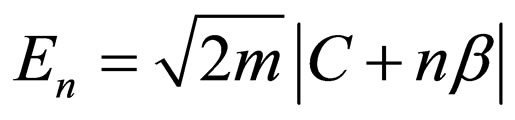 (67)
(67)
The equally-spaced energy levels are
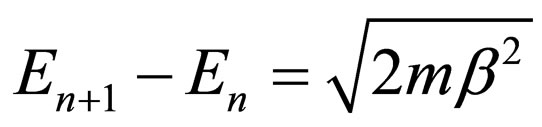 .
.
2) Considering Equation (45), if the potential is obtained using Equation (43) and following equation:
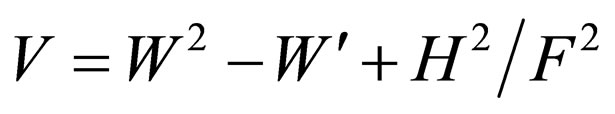 (68)
(68)
we will have:
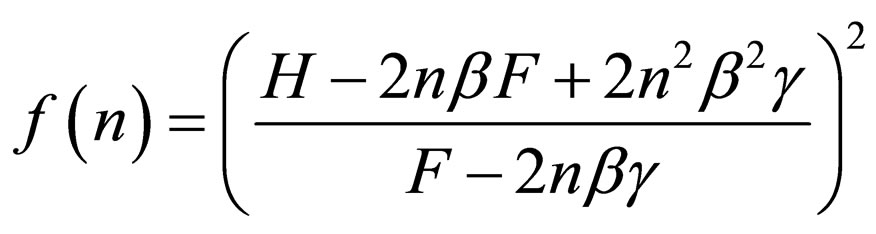 (69)
(69)
Consequently, with regard to Equations (63) and (69), its Klein-Gordon equation’s energies must be achieved using the following equation:
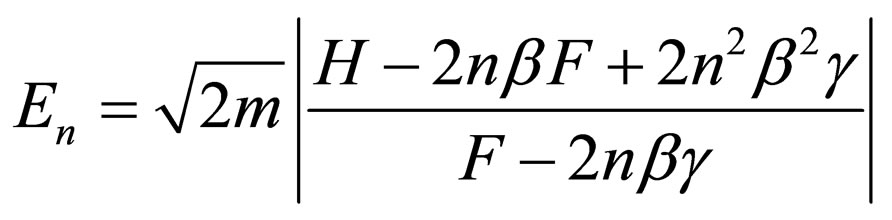 (70)
(70)
The special case 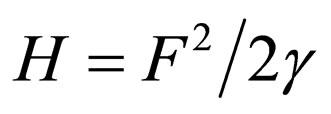 can be utilized to form equally-spaced levels, in which case we have:
can be utilized to form equally-spaced levels, in which case we have:
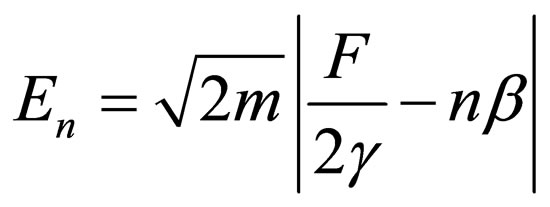 (71)
(71)
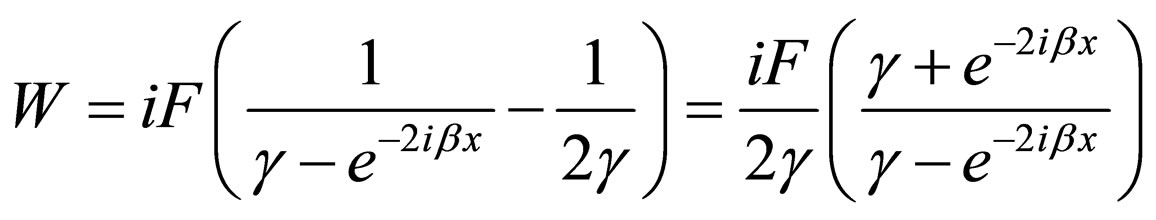 (72)
(72)
By considering Equation (68), for the potential 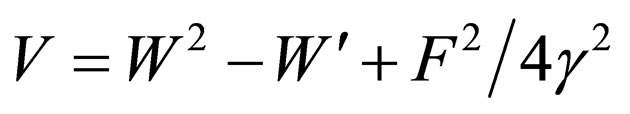 , the Klein-Gordon equation’s energies are acquired using Equation (71) having equallyspaced energy levels (
, the Klein-Gordon equation’s energies are acquired using Equation (71) having equallyspaced energy levels (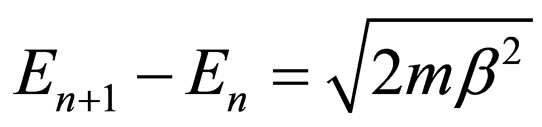 ).
).
3) Regarding Equation (61), if the potential is obtained using Equation (60) and the equation below:
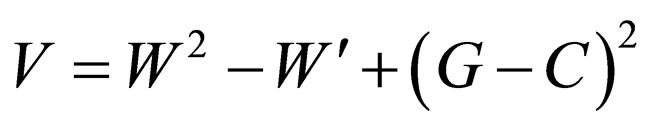 (73)
(73)
we will have:
 (74)
(74)
Therefore, through Equation (63), the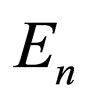 ’s include:
’s include:
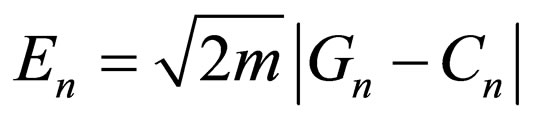 (75)
(75)
which is transformed into the following form using Equations (56) and (57):
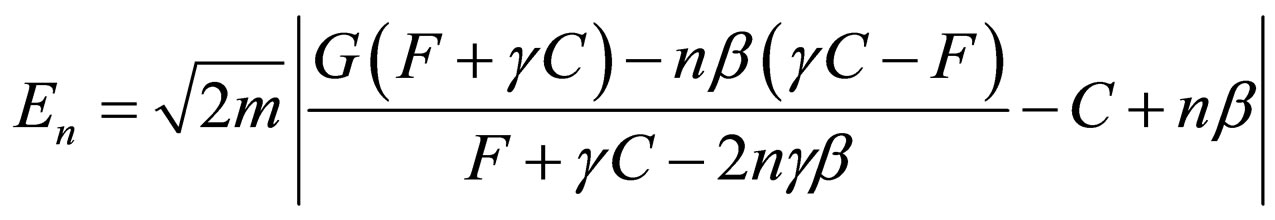 (76)
(76)
If the special case 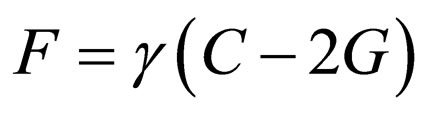 is used, Equation (76) is converted to:
is used, Equation (76) is converted to:
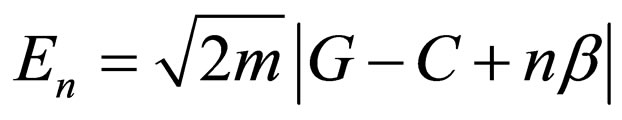 (77)
(77)
As a result, when the potential of Equation (73) is obtained by the following superpotential:
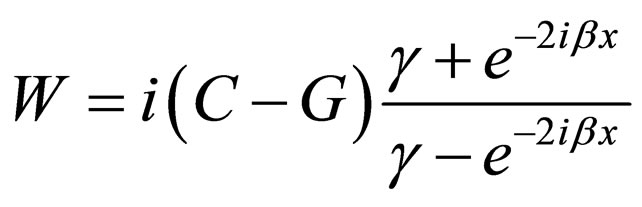 (78)
(78)
the Klein-Gordon equation’s energies with this potential are derived from Equation (77) having equaled-spaced energy levels (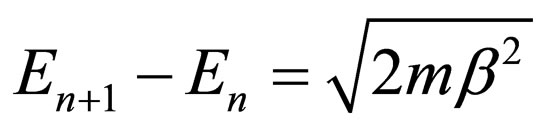 ).
).
It is evident that there is not a fundamental difference between Equations (72) and (78), but Equation (64) is more general than Equations (72) and (78).
5. Conclusions
Briefly, it can be said that we discovered three new superpotentials through these calculations. The first set includes the superpotential (26), transforms (27), and energies (29) or superpotential (30), transforms (31), and energies (33) having one variable parameter, and being transformed into the forms of Morse, generalized PöschlTeller, Pöschl-Teller I and II, and Scarf I and II superpotentials for specific values of parameters.
The second set includes the superpotential (34), transforms (40), and energies (42) or superpotential (43), transforms (44), and energies (45) having two variable parameters, and being transformed into the forms of Morse, Scarf II, Rosen-Morse I and II, and Pöschl-Teller I and II superpotentials for specific values of parameters.
The third set includes the superpotentials (46) and (60), transforms (55), (56), and (57), and energies (59) and (61) having three variable parameters, and being transformed into the forms of Morse, Eckart , and Rosen-Morse I and II superpotentials for specific values of parameters.
6. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry and Quantum Mechanics,” Physics Reports, Vol. 251, No. 5-6, 1995, pp. 267-385. doi:10.1016/0370-1573(94)00080-M
- F. Cooper, J. N. Ginocchio and A. Khare, “Relationship between Supersymmetry and Solvable Potentials,” Physical Review D, Vol. 36, No. 8, 1987, pp. 2458-2473.
- R. Dutt, A. Khare and U. P. Sukhatme, “Exactness of Supersymmetric WKB Spectra for Shape-Invariant Potentials,” Physics Letters B, Vol. 181, No. 3-4, 1986, pp. 295-298. doi:10.1016/0370-2693(86)90049-3
- J. W. Dabrowska, A. Khare and U. P. Sukhatme, “Explicit Wavefunctions for Shape-Invariant Potentials by Operator Techniques,” Journal of Physics A: Mathematical and General, Vol. 21, No. 4, 1988, pp. L195-L200. doi:10.1088/0305-4470/21/4/002
- F. Cooper, A. Khare and U. Sukhatme, “Periodic Solutions of Nonlinear Equations Obtained by Linear Superposition,” Journal of Physics A: Mathematical and General, Vol. 35, No. 47, 2002, pp. 10085-10100. doi:10.1088/0305-4470/35/47/309
- D. T. Barclay, R. Dutt, A. Gangopadhyaya, A. Khare, A. Pagnamenta and U. Sukhatme, “New Exactly Solvable Hamiltonians: Shape Invariance and Self-Similarity,” Physical Review A, Vol. 48, No. 4, 1993, pp. 2786-2797. doi:10.1103/PhysRevA.48.2786
- A. Khare and U. P. Sukhatme, “Scattering Amplitudes for Supersymmetric Shape-Invariant Potentials by Operator Methods,” Journal of Physics A: Mathematical and General, Vol. 21, No. 9, 1988, p. L501. doi:10.1088/0305-4470/21/9/005
- R. Adhikari, R. Dutt, A. Khare and U. P. Sukhatme, “Higher-Order WKB Approximations in Supersymmetric Quantum Mechanics,” Physical Review A, Vol. 38, No. 4, 1988, pp. 1679-1686. doi:10.1103/PhysRevA.38.1679
- R. Dutt, A. Khare and U. P. Sukhatme, “SupersymmetryInspire WKB Approximation in Quantum Mechanics,” American Journal of Physics, Vol. 59, No. 8, 1991, pp. 723-727. doi:10.1119/1.16840
- A. Khare and U. P. Sukhatme, “New Shape-Invariant Potentials in Supersymmetric Quantum Mechanics,” Journal of Physics A: Mathematical and General, Vol. 26, 1993, pp. L901-L904. doi:10.1088/0305-4470/26/18/003
- U. P. Sukhatme, C. Rasinariu and A. Khare, “Cyclic Shape Invariant Potentials,” Physics Letters A, Vol. 234, No. 6, 1997, pp. 401-409. doi:10.1016/S0375-9601(97)00555-0
- A. Khare and U. P. Sukhatme, “Linear Superposition in Nonlinear Equations,” Physical Review Letters, Vol. 88, No. 24, 2002, pp. 244101-244104. doi:10.1103/PhysRevLett.88.244101
- W. Keung, E. Kovacs and U. P. Sukhatme, “Supersymmetry and Double-Well Potentials,” Physical Review Letters, Vol. 60, No. 41, 1988, pp. 41-44. doi:10.1103/PhysRevLett.60.41
- S. Chaturvedi, R. Dutt, A. Gangopadhyaya, P. Panigrahi, C. Rasinariu and U. Sukhatme, “Algebraic Shape Invariant Models,” Physics Letters A, Vol. 248, No. 2-4, 1998, pp. 109-113. doi:10.1016/S0375-9601(98)00636-7
- R. De, R. Dutt and U. Sukhatme, “Mapping of Shape Invariant Potentials under Point Canonical Transformations,” Journal of Physics A: Mathematical and General, Vol. 25, No. 13, 1992, pp. L843-L850. doi:10.1088/0305-4470/25/13/013
- A. Gangopadhyaya, A. Khare and U. P. Sukhatme, “Methods for Generating Quasi-Exactly Solvable Potentials,” Physics Letters A, Vol. 208, No. 4, 1995, pp. 261-268. doi:10.1016/0375-9601(95)00824-3
- M. Hruska, W. Keung and U. Sukhatme, “Accuracy of Semiclassical Methods for Shape-Invariant Potentials,” Physical Review A, Vol. 55, No. 5, 1997, pp. 3345-3350. doi:10.1103/PhysRevA.55.3345
- A. Khare and U. P. Sukhatme, “Cyclic Identities Involving Jacobi Elliptic Functions,” Journal of Mathematical Physics, Vol. 43, No. 7, 2002, pp. 3798-3806. doi:10.1063/1.1484541
- A. Gangopadhyaya, J. V. Mallow and U. P. Sukhatme, “Translational Shape Invariance and the Inherent Potential Algebra,” Physics Letters A, Vol. 58, No. 3, 1998, pp. 4287-4292.
- F. Cooper, J. N. Ginocchio and A. Wipf, “Derivation of the S-Matrix Using Supersymmetry,” Physics Letters A, Vol. 129, No. 3, 1988, pp. 145-147. doi:10.1016/0375-9601(88)90131-4
- A. Khare and U. Sukhatme, “Phase-Equivalent Potentials Obtained from Supersymmetry,” Journal of Physics A: Mathematical and General, Vol. 22, No. 14, 1989, p. 2847. doi:10.1088/0305-4470/22/14/031
- J. Pappademos, U. Sukhatme and A. Pagnamenta, “Bound States in the Continuum from Supersymmetric Quantum Mechanics,” Physical Review A, Vol. 48, No. 3525, 1993, pp. 3525-3531. doi:10.1103/PhysRevA.48.3525
- F. Cooper, A. Khare, B. Mihaila and A. Saxena, “Exact Solitary Wave Solutions for a Discrete λ
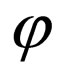 4 Field Theory in 1 + 1 Dimensions,” Physical Review E, Vol. 72, No. 3, 2005, Article ID 036605.
4 Field Theory in 1 + 1 Dimensions,” Physical Review E, Vol. 72, No. 3, 2005, Article ID 036605. - A. Gangopadhyaya and U. P. Sukhatme, “Potentials with Two Shifted Sets of Equally Spaced Eigenvalues and Their Calogero Spectrum,” Physics Letters A, Vol. 224, No. 1-2, 1996, pp. 5-14. doi:10.1016/S0375-9601(96)00807-9
- R. Dutt, A. Gangopadhyaya, A. Khare, A. Pagnamenta and U. Sukhatme, “Solvable Quantum Mechanical Examples of Broken Supersymmetry,” Physics Letters A, Vol. 174, No. 5-6, 1993, pp. 363-367. doi:10.1016/0375-9601(93)90191-2
- A. Gangopadhyaya, J. V. Mallow and U. P. Sukhatme, “Broken Supersymmetric Shape Invariant Systems and Their Potential Algebras,” Physics Letters A, Vol. 283, No. 5, 2001, pp. 279-284. doi:10.1016/S0375-9601(01)00266-3
- A. Khare and U. Sukhatme, “Analytically Solvable PTInvariant Periodic Potentials,” Physics Letters A, Vol. 324, 2004, pp. 406-414. doi:10.1016/j.physleta.2004.03.006
- R. Dutt, A. Gangopadhyaya, A. Khare, A. Pagnamenta and U. Sukhatme, “Semiclassical Approach to QuantumMechanical Problems with Broken Supersymmetry,” Physical Review A, Vol. 48, No. 3, 1993, pp. 1845-1853. doi:10.1103/PhysRevA.48.1845
- W. Keung, U. P. Sukhatme, Q. Wang and T. D. Imbo, “Families of Strictly Isospectral Potentials,” Journal of Physics A: Mathematical and General, Vol. 22, No. 21, 1989, pp. L987-L992. doi:10.1088/0305-4470/22/21/002
- P. K. Panigrahi and U. P. Sukhatme, “Singular Superpotentials in Supersymmetric Quantum Mechanics,” Physics Letters A, Vol. 178, No. 3-4, 1993, pp. 251-257. doi:10.1016/0375-9601(93)91098-P
- F. Cooper, A. Khare, R. Musto and A. Wipf, “Supersymmetry and the Dirac Equation,” Annals of Physics, Vol. 187, No. 1, 1988, pp. 1-28. doi:10.1016/0003-4916(88)90279-5
- M. S. Kumar and A. Khare, “Coherent States for Isospectral Hamiltonians,” Physics Letters A, Vol. 217, No. 2-3, 1996, pp. 73-77. doi:10.1016/0375-9601(96)00332-5
- F. Cooper, J. N. Ginocchio and A. Wipf, “Supersymmetry, Operator Transformations and Exactly Solvable Potentials,” Journal of Physics A: Mathematical and General, Vol. 22, No. 17, 1989, pp. 3707-3716. doi:10.1088/0305-4470/22/17/035
- R. Dutt, A. Khare and Y. P. Varshni, “New Class of Conditionally Exactly Solvable Potentials in Quantum Mechanics,” Journal of Physics A: Mathematical and General, Vol. 28, No. 3, 1995, p. L107. doi:10.1088/0305-4470/28/3/008
- A. Khare, K. Rasmussen, M. Salerno, M. R. Samuelsen and A. Saxena, “Discrete Nonlinear Schrödinger Equations with Arbitrarily High-Order Nonlinearities,” Physical Review E, Vol. 74, No. 1, 2006, Article ID 016607.
- A. Khare, “Parasupersymmetric Quantum Mechanics of Arbitrary Order,” Journal of Physics A: Mathematical and General, Vol. 25, No. 12, 1992, p. L749. doi:10.1088/0305-4470/25/12/008
- A. Khare and Y. P. Varshni, “Is Shape Invariance Also Necessary for Lowest Order Supersymmetric WKB to Be Exact?” Physics Letters A, Vol. 142, No. 1, 1989, pp. 1-4. doi:10.1016/0375-9601(89)90701-9
- R. Dutt, A. Gangopadhyaya, C. Rasinariu and U. Sukhatme, “New Solvable Singular Potentials,” Journal of Physics A: Mathematical and General, Vol. 34, No. 19, 2001, p. 4129. doi:10.1088/0305-4470/34/19/311
- E. Harikumar, V. S. Kumar and A. Khare, “Supersymmetric Quantum Mechanics on Non-Commutative Plane,” Physics Letters B, Vol. 589, No. 3-4, 2004, pp. 155-161. doi:10.1016/j.physletb.2004.03.042
- A. Gangopadhyaya, P. K. Panigrahi and U. P. Sukhatme, “Supersymmetry and Tunneling in an Asymmetric Double Well,” Physical Review A, Vol. 47, No. 4, 1993, pp. 2720-2724. doi:10.1103/PhysRevA.47.2720
- R. Dutt, A. Khare and U. P. Sukhatme, “Supersymmetry, Shape Invariance, and Exactly Solvable Potentials,” American Journal of Physics, Vol. 56, No. 2, 1988, p. 163. doi:10.1119/1.15697
- C. X. Chuan, “Exactly Solvable Potentials and the Concept of Shape Invariance,” Journal of Physics A: Mathematical and General, Vol. 24, No. 19, 1991, p. L1165. doi:10.1088/0305-4470/24/19/008
- C. X. Chuan, “Odd Potentials in Supersymmetric Quantum Mechanics,” Journal of Physics A: Mathematical and General, Vol. 23, No. 13, 1990, p. L659. doi:10.1088/0305-4470/23/13/005
- C. X. Chuan, “The Theory of Coupled Differential Equations in Supersymmetric Quantum Mechanics,” Journal of Physics A: Mathematical and General, Vol. 23, No. 23, 1990, p. L1217. doi:10.1088/0305-4470/23/23/006
- C. X. Chuan, “Some Solvable Eigenvalue Problems,” International Journal of Theoretical Physics, Vol. 34, No. 9, 1995, pp. 1907-1914. doi:10.1007/BF00674072
- C. X. Chuan, “Alternative Approach to the Concept of Shape Invariance in Quantum Mechanics,” International Journal of Theoretical Physics, Vol. 37, No. 9, 1998, pp. 2439-2448. doi:10.1023/A:1026679311801
- C. X. Chuan, “Higher Order Generation of Exactly Solvable Supersymmetric Systems,” International Journal of Theoretical Physics, Vol. 38, No. 2, 1999, pp. 745-756. doi:10.1023/A:1026671710777
- T. Barakat, M. Odeh and O. Mustafa, “Perturbed Coulomb Potentials in the Klein-Gordon Equation via the Shifted-l Expansion Technique,” Journal of Physics A: Mathematical and General, Vol. 31, No. 15, 1998, p. 3469. doi:10.1088/0305-4470/31/15/012
- H. Egrifes and R. Sever, “Bound-State Solutions of the Klein-Gordon Equation for the Generalized PT-Symmetric Hulthén Potential,” International Journal of Theoretical Physics, Vol. 46, No. 4, 2007, pp. 935-950. doi:10.1007/s10773-006-9251-8
- T. Barakat, “Perturbed Coulomb Potentials in the KleinGordon Equation via the Asymptotic Iteration Method,” Annals of Physics, Vol. 324, No. 3, 2009, pp. 725-733. doi:10.1016/j.aop.2008.10.008
- M. M. Panja, R. Dutt and Y. P. Varshni, “Shifted Large-N Expansion for the Power-Law Potentials in the KleinGordon Equation with Applications,” Journal of Physics A: Mathematical and General, Vol. 22, No. 15, 1989, p. 2291. doi:10.1088/0305-4470/22/15/015
- Y. Chargui, L. Chetouani and A. Trabelsi, “Exact Solution of the One-Dimensional Klein-Gordon Equation with Scalar and Vector Linear Potentials in the Presence of a Minimal Length,” Chinese Physics B, Vol. 19, No. 2, 2010, Article ID 020305. doi:10.1088/1674-1056/19/2/020305
- Y. Nedjadi, S. Ait-Tahar and R. C. Barrett, “An Extended Relativistic Quantum Oscillator for S = 1 Particles,” Journal of Physics A: Mathematical and General, Vol. 31, No. 16, 1998, p. 3867. doi:10.1088/0305-4470/31/16/014
- J. B. Wang, J. F. Williams, A. T. Stelbovics, J. E. Furst and D. H. Madison, “Coherent Excitation of the SingletTriplet Mixed 1s4f State of Helium,” Physical Review A, Vol. 52, No. 4, 1995, pp. 2885-2900. doi:10.1103/PhysRevA.52.2885
- P. F. Smith, “Coherent Neutrino Scattering—Relativistic and Nonrelativistic,” Il Nuovo Cimento A, Vol. 83, No. 3, 1984, pp. 263-274. doi:10.1007/BF02902601
- G. Ni, J. Xu and W. Chen, “The Thermal Coherent State and Its Application to the One-Dimensional Field Theory,” Journal of Physics A: Mathematical and General, Vol. 18, No. 1, 1985, pp. 149-164. doi:10.1088/0305-4470/18/1/026
- A. Messina and F. Persico, “Spontaneous Coherent Phonons in the Ground State of Strong Spin-Phonon Interaction,” Journal of Physics C: Solid State Physics, Vol. 6, No. 24, 1973, pp. 3557-3570. doi:10.1088/0022-3719/6/24/016
NOTES
*Corresponding author.

