450px;">

Journal of Modern Physics
 Vol.3 No.7(2012), Article ID:21076,8 pages DOI:10.4236/jmp.2012.37071

Negative Magnetoresistance Behaviour and Variable Range Hopping Conduction in Insulating NbSi Amorphous Alloys at Very Low Temperature with Magnetic Field

Abdelghani Sybous1, Abdelhamid El Kaaouachi1*, Jamal Hemine2, Abdelfattah Narjis1, Lhoussine Limouny1, Said Dlimi1, Rachid Abdia3, Gerard Biskupski3

1Research Group in ESNPS, Physics Department, Faculty of Sciences, University Ibn Zohr, Agadir, Morocco

2Laboratoire de Physique de la Matière Condensée, Département de Physique, Faculté des Sciences et Techniques de Mohammadia, Mohammedia, Morocco

3Laboratoire de Spectroscopie Hertzienne (LSH), Université des Sciences et Technologies de Lille I, Villeneuve d’Ascq, France

Email: *kaaouachi21@yahoo.fr

Received September 12, 2011; revised October 12, 2011; accepted November 12, 2011

Keywords: NbSi amorphous alloys; Negative magnetoresistance; Magnetic field; localized magnetic Moments; quantum interference

ABSTRACT

We present results of an experimental study of magnetoresistance (MR) in insulating NbSi amorphous alloys sample showing Variable Range Hopping (VRH) conductivity. The MR is found to be negative in a wide range of low temperature (4.2 - 20 K) and in the range of moderate magnetic fields (0 - 4 T). We made tentative analysis using three theoretical models which are the model of quantum interference, the model of Zeeman effect and the model of localized magnetic moments

1. Introduction

For few decades, the negative magnetoresistance (NMR) of doped semiconductors has been the subject of investigations, as much in the metallic regime [1-3] as in insulating systems [4,5]. The most recent theories are based on the quantum corrections, which are enhanced in the neighbourhood of the Metal-Insulator Transition (MIT). The quantum interference models seem to describe accurately the NMR of metallic materials [6,7].

For insulating samples, theories on quantum interference effects in the variable range hopping (VRH) regime [8] is in a good agreement with experiment for very low magnetic fields. On the other hand, Toyozawa [9] proposed that the negative magnetoresistance is a consequence of alignment of local magnetic moments by the applied magnetic field. This alignment decreases the magnetic scattering of electrons and reduces the electrical resistivity. The experimental magnetoresistance (MR) are plotted as a function of magnetic field in Figure 1. A negative MR is observed below 10 K with an unusual magnitude of about 10% at the lowest temperatures.

In order to consider only the negative part of the MR (Figure 2), the present paper is devoted to a tentative analysis of the negative MR of insulating a-NbSi sample in the temperature range 4.2 - 20 k and in magnetic fields up to 2.5 T using several theoretical models. Bishop et al. [10] have obtained a Metal-Insulator Transition (MIT) in this a-NbSi system at an atomic concentration of 88.7% Si. Our sample is situated in the insulating side of the MIT and referenced Nb11Si89. The Variable Range Hopping (VRH) conduction has been observed in this sample, and all the conductivity data, for different magnetic fields, follows a universal VRH law given by:

(1)

where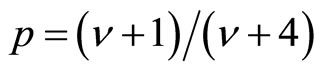. When, the Density of State (DOS) is constant and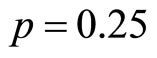, corresponding to the Mott VRH regime. But when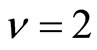, the DOS varies in the vicinity of the Fermi level and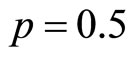, corresponding to the Efros and Schklovskii (ES) VRH regime. In fact, The VRH of the three dimensional disordered systems, like doped semiconductors were shown by Mott [11,12] to behave like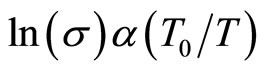. This dependence

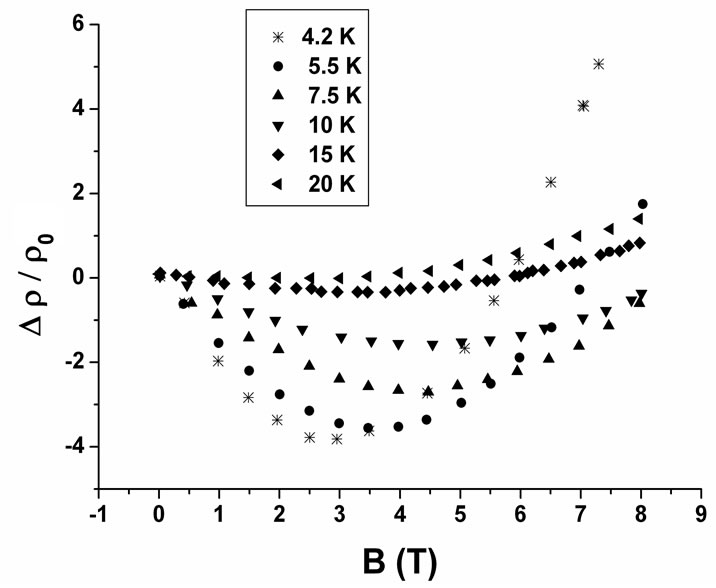
Figure 1. Negative MR versus magnetic field for several temperatures.

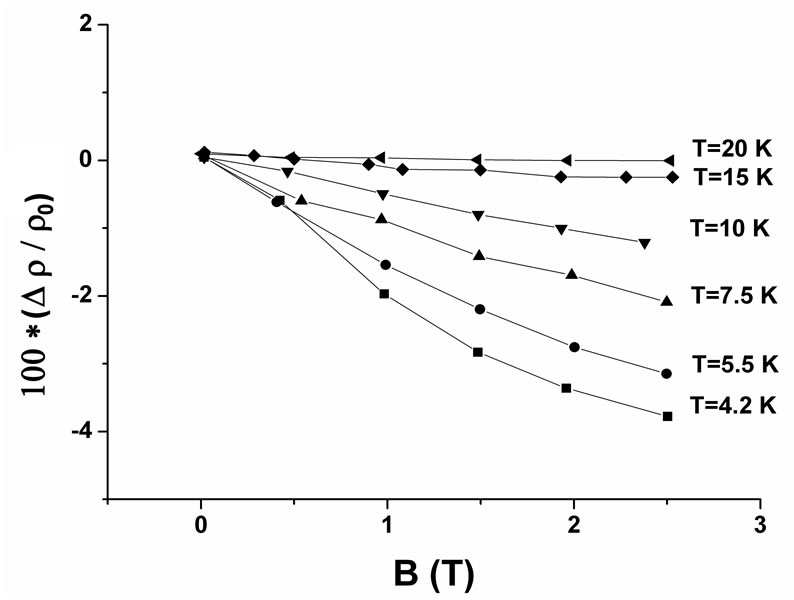
Figure 2. Negative MR versus magnetic field for several temperatures in magnetic fields up to 2.5 T.

was obtained by optimizing the hopping probability and assuming a slowly varying DOS in the vicinity of the Fermi level. Mott VRH has been widely observed in many types of disordered materials [13-16].

On the contrary, ES [17,18] have predicted that long range electron-electron interaction reduces the DOS at the Fermi level and creates a soft Coulomb Gap (CG), which takes the form, with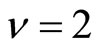. The existence of the CG leads to the ES VRH regime of the conductivity. However, the experimental situation has been confusing for some time, with both values of being observed [19,20].

In Figures 3 and 4, we plot respectively 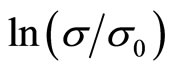 against 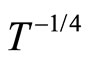and 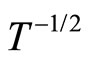for several values of magnetic field. It can be seen that it is difficult to choose between the Mott VRH regime with 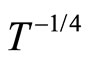and the ES VRH regime with.

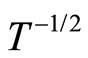In this work we have attempted to decide for one of the two VRH regimes by studying the behaviour of negative magnetoresistance.

2. Quantum Interference

The manifestation of quantum interference has received

Figure 3. 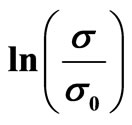against 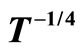for several values of magnetic field.

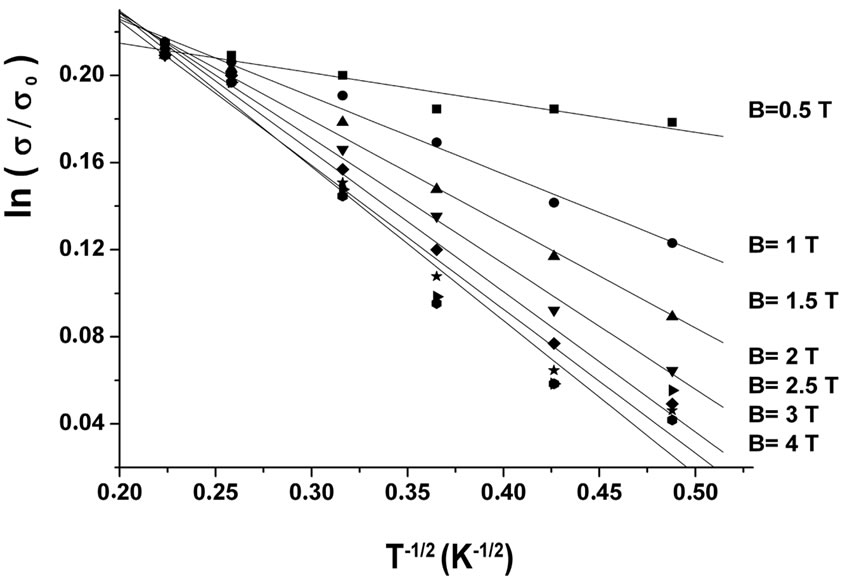
Figure 4. 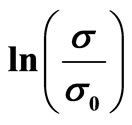against 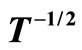for several values of magnetic field.

considerable attention in the properties of disordered systems. The low field NMR in disordered conductors has been studied and understood in terms of a suppression of quantum localization corrections in the Drude equation for the conductivity [1,9]. As Holstein [21] first noted in his seminal work on the Hall coefficient, quantum interference is also an important issue in disordered insulators where the transport at low temperature is dominated by phonon-assisted hopping. Theoretical studies [22-25] indicate that the magnetoconductance (MC) is positive in the VRH regime, as it is for weak localization. The positive MC in the VRH regime has been attributed to the effect of a magnetic field on the quantum interference between forward-scattering events.

Theories on quantum interference effects in the VRH regime have been proposed in references [22,23] and [24,25]. In these references, interference among the paths are associated to the hopping between two sites at a distance 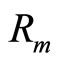apart, where 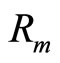is the optimum hopping length. It is shown that this interference affects the hopping probability between these two sites. In the first case [22,23], by averaging numerically the logarithm of the conductivity over many random impurity realizations, a net linear decrease in resistivity with magnetic field is found. In the second case [24,25], the calculations are based on a critical path analysis and NMR, quadratic in the flux through an effective area 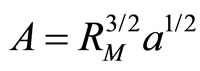is predicted, where 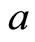is the typical distance between impurities.

This gives:

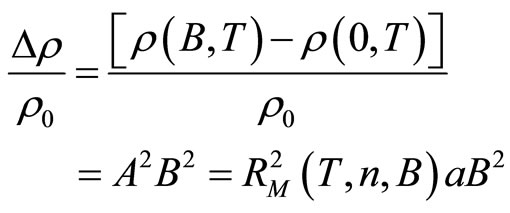(2)

where 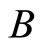is the applied magnetic field.

For a given sample and in small magnetic field where 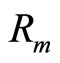is at most weak function of the field:

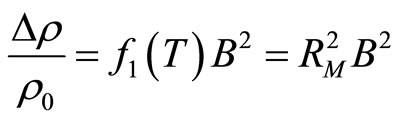(3)

The temperature dependence of the hopping length 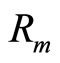should determine the temperature dependence of the magnetoresistance. In three-dimensional systems where Mott VRH regime is observed 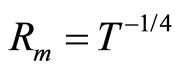and Equation (3) predicts that:

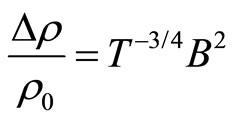(4)

In the present of a CG in the DOS associated with Coulomb corrections, the hopping length diverges more rapidly as 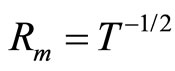, and one expects:

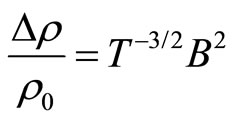(5)

Quadratic NMR with magnetic field has been observed experimentally in the VRH regime in a number of insulating materials [26,27]. Schirmacher [28] proposed another analysis of NMR in presence of VRH regime using the following expression:

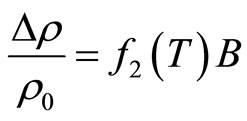(6)

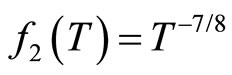
3. Zeeman Effect

Fukuyama and Yosida [29] have proposed a mechanism to explain NMR behaviour in the VRH regime with magnetic field. According to these authors, the application of a magnetic field induces a cleavage of eigenstates degenerate to Zeeman sub-levels, and the repopulation of energy levels in which the majority of the holders are in the Zeeman higher state [29]. This state is closer to the mobility edge . The wave function that corresponds to this state has a larger spatial extension, causing therefore a NMR given by:

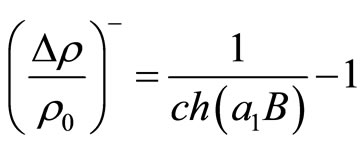(7)

where 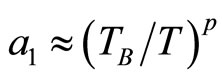with 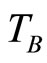is the characteristic temperature depending on magnetic field.  corresponding to the Mott VRH regime with and to the ES VRH regime with.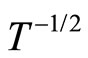

4. Model of Localized Magnetic Moments

According to Toyozawa [9], the conduction electrons are scattered by the localized magnetic moments of impurities. The application of an external magnetic field orders these magnetic moments, so that the conductivity increases.

Yosida [30] has likened this system to a set of paramagnetic spins. The negative MR is then approached by a Curie-Weiss law:

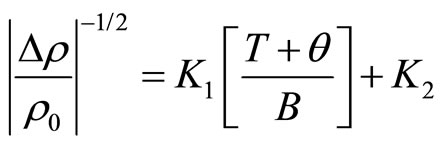(8)

where 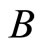 is the magnetic field and a temperature which may be considered as the Curie temperature of the paramagnetic system.

On the other hand, if magnetic moments exist, the magnetoresistance is proportional to the square of the average magnetization of impurities, which is described by a Brillouin function 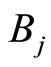in the classical theories of paramagnetic systems:

(9)

where  is the Bohr magneton, the effective magnetic moment of scattering centers, 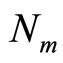 the concentration of scattering centers and indicates the total moment of localized electrons, as in the case of negative MR study, the magnetization becomes proportional to a classical Langevin function:

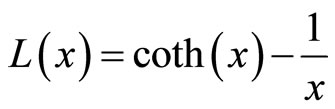(10)

where

(11)

Thus, the negative MR stemming from the spin diffusion takes the following form:

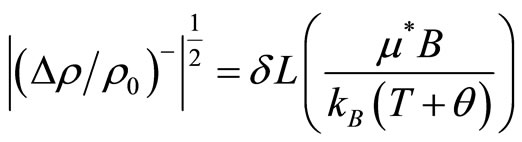(12)

where 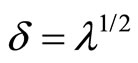is a constant. We emphasize here that the total MR is, in fact, the sum of both negative and positive contributions:

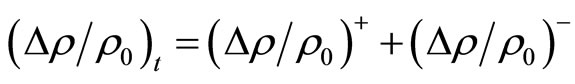
where the positive MR is given by the expression of Shklovskii and Efros [31] for the classically moderate field:

(13)

The parameter 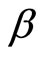has been evaluated for each temperature in the high field region and the positive MR has been subtracted from the total MR, in order to consider only the negative part of the MR (Figure 2). In previous papers we have analyzed the positive MR given by Equation (13) in the different samples of CdSe [32,33] and InP [34,35].

5. Results, Discussion and Conclusion

In this work, we will try to apply these theoretical models with our experimental results of NMR. First, we used the model of quantum interference. During the adjustments, the magnetic field is reduced so as to take the part of the magnetoresistance which we can apply this theory. Figure 5, shows the evolution of the NMR 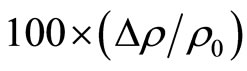 with the magnetic field B at different temperatures. We observed that in the limit of low fields, the NMR varies linearly with  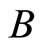and the slopes 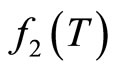of these straight lines decrease when the temperature increases. We also noticed that the value of magnetic field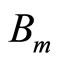, from which the linearity deviation occurs increases with temperature, which is in good agreement with the model of Schirmacher [28]. We have determined the slopes  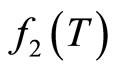for each temperature Equation (6). Figure 6 shows the variation of 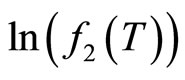against. 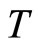We have noticed that varies with temperature as 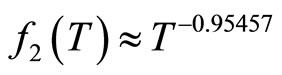. The value of the slope is very close to the value −7/8 predicted by theory [28].

For, the variation of NMR becomes linear with 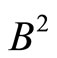(Figure 7), which is in good agreement with

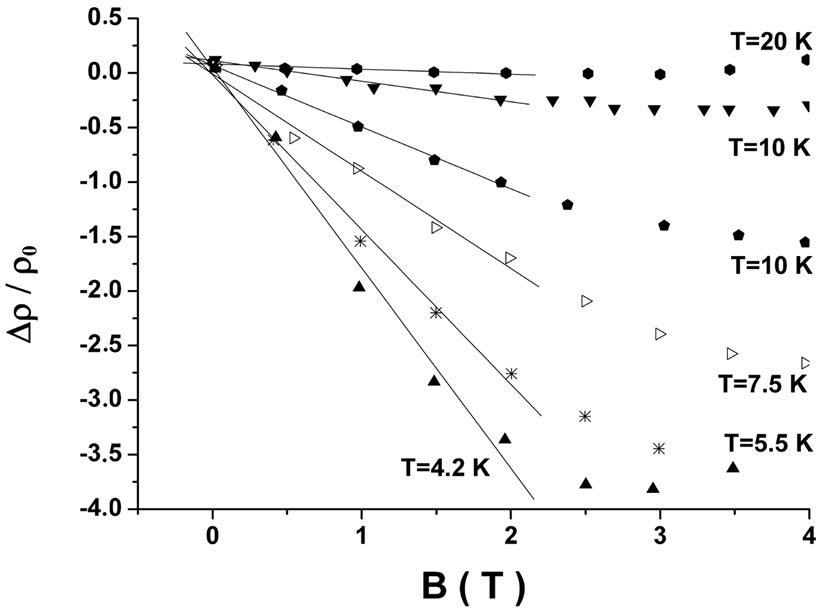
Figure 5. Negative MR against b at different temperatures.

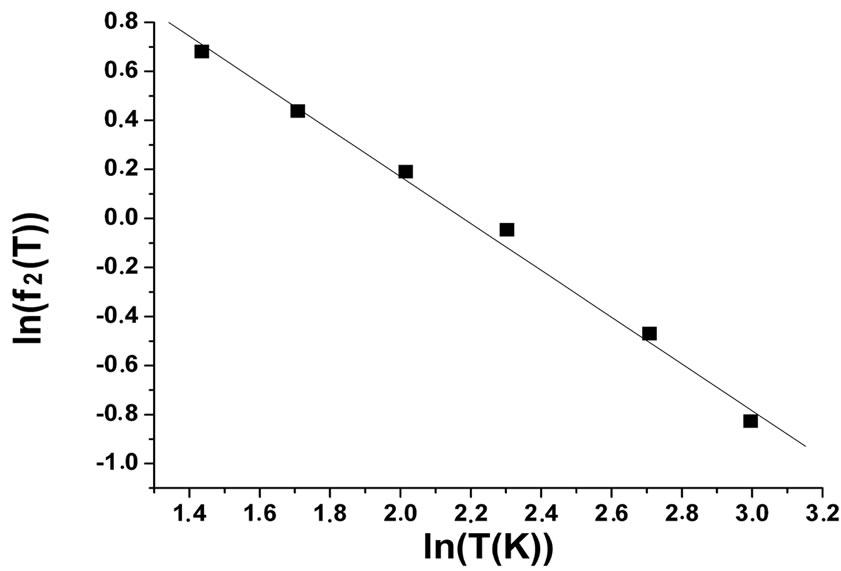
Figure 6. Variation of ln(f2(T)) with ln(T).

Figure 7. Negative MR against b2 at different temperatures.

the theory proposed by Entin-Wolhman [25]. The NMR has been adjusted using the following from: 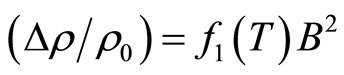. To show the dependence of the NMR with the temperature, we plot in Figure 8 the variation of versus. We observed that the curve obtained can be adjusted by a straight lines that give us the law: 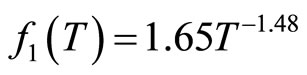(Equation (5)). The slope is equal to −1.48, which is very close to −3/2 predicted by the theory in ES VRH regime (Equation (5)).

We noticed that this variation can be associated with the ES VRH regime 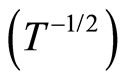. Several experimental measurements of NMR have been confronted with the theoretical expression of Entin-Wohlman on many insulating materials. The authors found consistent results with theoretical predictions of quantum interference in the two VRH regimes of Mott and of Efros Shklovskii [26,37- 39].

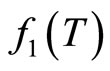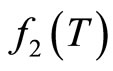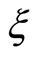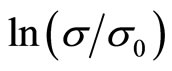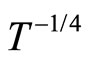On the other hand, within the limits of the fields where the NMR has been studied theoretically using the model of quantum interference, the approximations suggest an independence or weak dependence of parameters and, and in particular of the localization length with the magnetic field. If we go back to examine the variation of with  (Figure 3) we noticed that curves show straight lines of negative slope

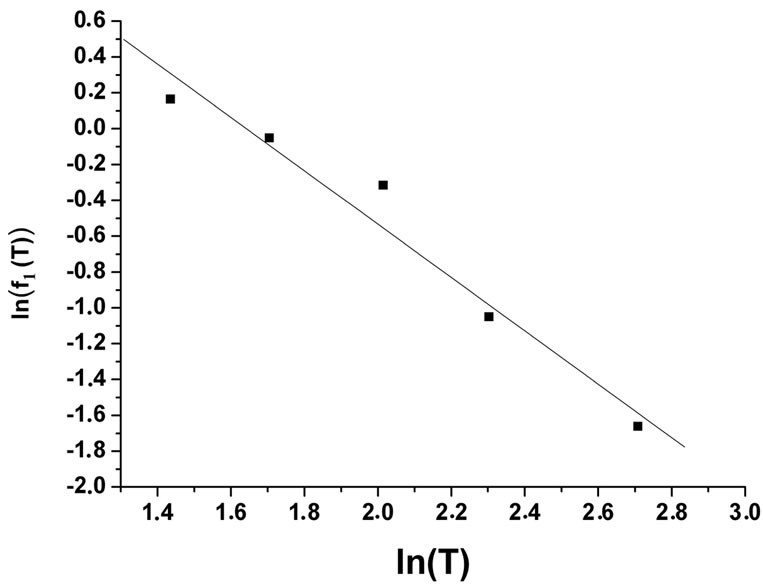
Figure 8. Variation of the parameter ln(f1(T)) versus ln(T).

which decreases with the magnetic field. This behaviour confirms the variation and the dependence of the localization length 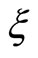with magnetic field.

We concluded that in this a-Nb11Si89 sample, the NMR can be interpreted by quantum interference effects and show the existence of the ES VRH conduction regime.

Secondly, we try to adjust our NMR using the theory of Zeeman effect expressed by Equation (7). We apply this expression of the NMR to our experimental results for different temperatures (Figure 9) with an adjustable parameter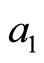. The adjusted values of the parameter 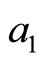are shown in Figure 10. varies with temperature as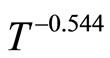. These results are in good agreement with the presence of the ES VRH regime 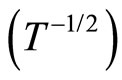. On the other hand, if we assume, as Benzaquen [39], that in the range of low magnetic field, the characteristic temperature is independent of the magnetic field 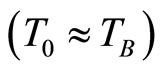, we can make a comparison between the adjusted values and theoretical values of 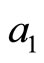(Table 1).

Despite the good agreement in the dependence of parameter 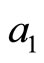as a function of temperature between the adjusted values and theoretical values in the ES VRH regime 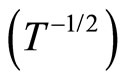confirming the existence of the ES VRH conduction regime in our a-Nb11Si89 sample. The qualitative disagreement is accentuated (Figure 9) as in the case of CuInSe2 [39] and GaAs [40]. A relatively low magnetic field lifts the degeneracy of the spin eigenstates situated near the Fermi level. We believe that the theoretical model of the Zeeman effect would be particularly appropriate in the critical region of the metal-insulator transition on the insulator side.

Third, we try to analyze our NMR behaviour using the model of magnetic model. In a first approach, following the Equation (12), the Curie temperature 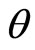has been evaluated by plotting  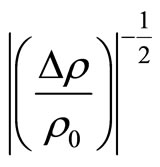as a function of the temperature for each value of the magnetic field. Figure 11, clearly exhibits a set of straight lines which, if extended to the low temperature limit, are secant at a point

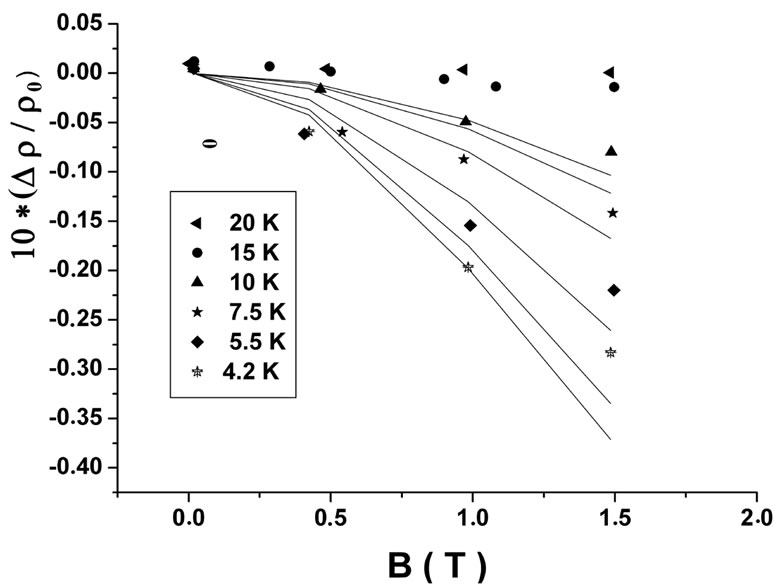
Figure 9. Variation of experimental NMR and theoretical NMR (solid line) using the theory of Zeeman effect with magnetic field.

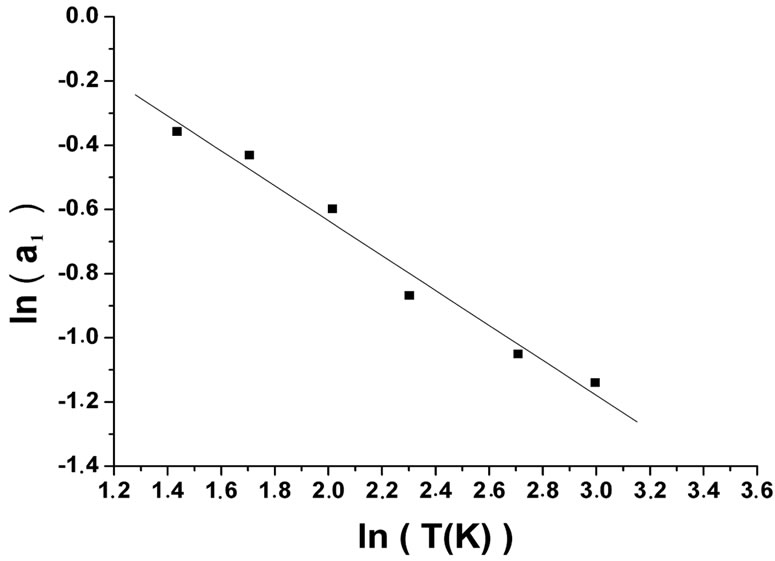
Figure 10. Variation of the adjusted parameter a1 in Equation (7) with temperature.

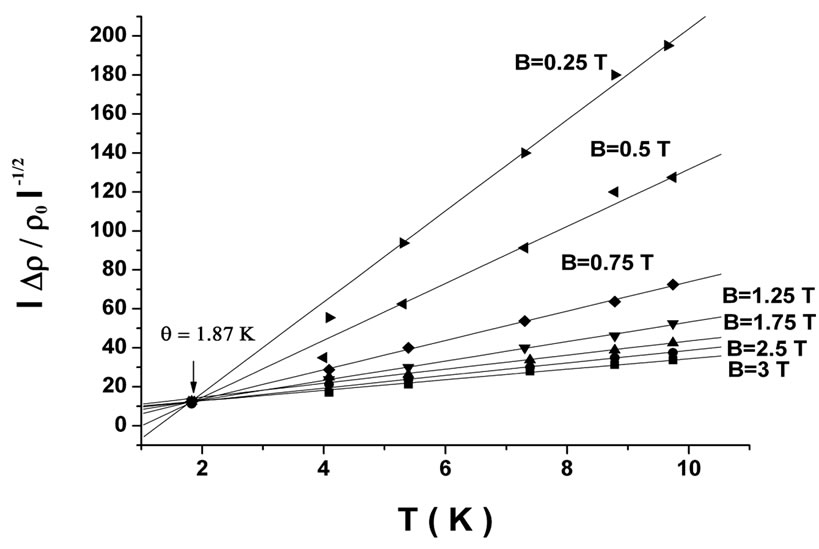
Figure 11. Inverse square root of the NMR against temperature at deferent magnetic fields.

of coordinates . The Curie temperature 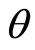is estimated at about 1.87 K. the fit of the negative MR by the Langevin function allows a more accurate evaluation of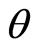. On the Figure 12 is plotted 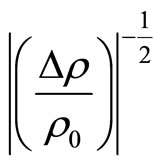versus the ratio 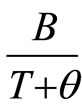, for temperature varying

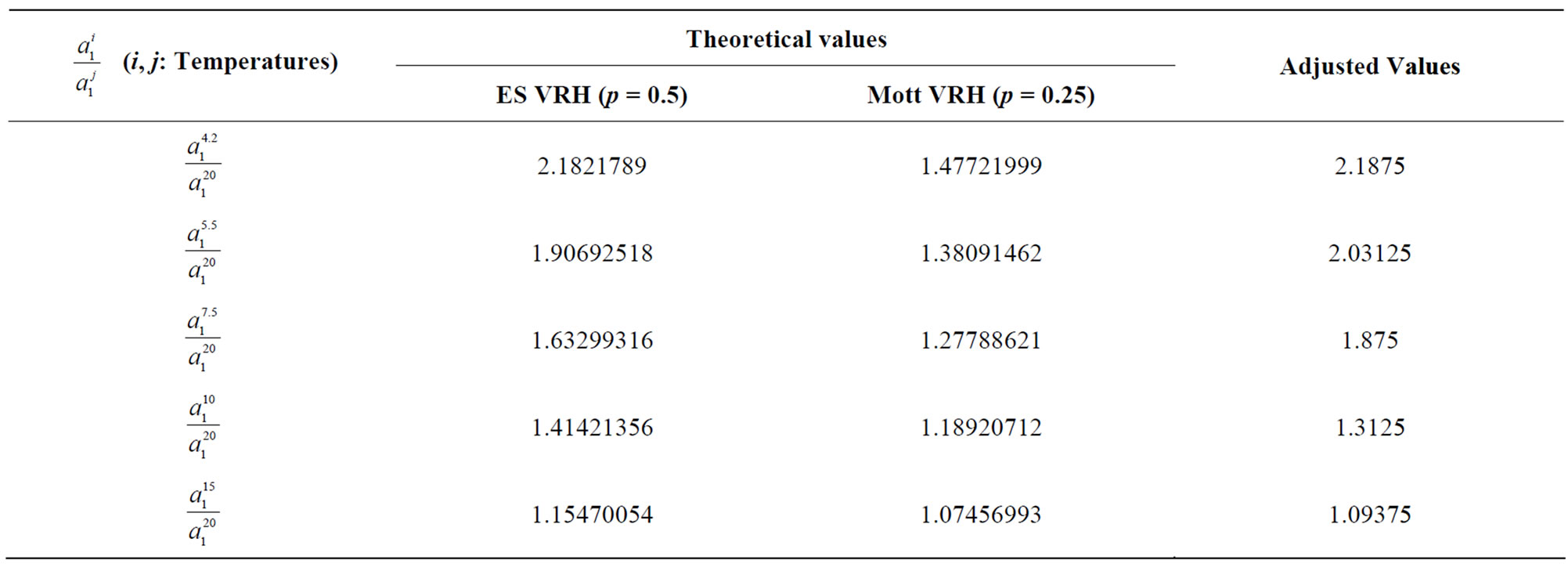
Table 1. Adjusted and theoretical values of parameter a1 in Equation (7).

Figure 12. Square root of the negative component of the MR against the ratio for different sets of values for B and T. the solid line represents the Langevin function fitted with 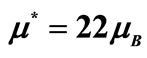and

between 4.2 K and 20 K and magnetic fields between and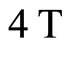. The better fit is obtained for  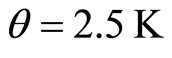and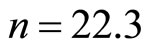

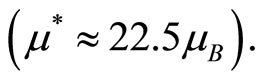
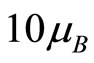According to Toyozawa [9], the existence of a negative MR is based on the assumption that the value of lies between 5 and . This interval is explained as the result of the collective nature of the magnetic moment in the study of statistical distribution of the localized spins. This value of is about twice as large as 10 who is the maximum of n proposed by Toyosawa [9]. This theoretical model does not give us a value of n in the range proposed by Toyozawa (5 < n < 10). We conclude that our negative magnetoresistance cannot be explained by this model.

The model of localized moments for negative MR has been previously tested successfully on metallic InP [41], insulating CdAs2 [42] and Al-doped ZnO metallic thin films [43] samples. In these materials, the theoretical model is very consistent with experience and the effective magnetic moment values are included in the range defined by Toyozawa.

REFERENCES

  1. A. Kawabata, “Theory of Negative Magnetoresistance in Three-Dimensional Systems,” Solid State Communications, Vol. 34, No. 6, 1980, pp. 431-432. doi:10.1016/0038-1098(80)90644-4
  2. B. L. Altshuler, A. G. Aronov, A. I. Larkin and D. E. Khmelnitski, “Positive Quasiclassical Magnetoresistance and Quantum Effects in Germanium Quantum Wells,” Low Temperature Physics, Vol. 36, No. 12, 2010, Article ID: 1076. doi:10.1063/1.3536348
  3. T. A. Dauzhenka, V. K. Ksenevich, I. A. Bashmakov and J. Galibert, “Origin of Negative Magnetoresistance in Polycrystalline SnO2 Films,” Physical Review B, Vol. 83, No. 16, 2011, Article ID: 165309. doi:10.1103/PhysRevB.83.165309
  4. V. L. Nguyen, B. Z. Spivak and B. I. Shklovskii, “Aharonov-Bohm Oscillations with Normal and Superconductive Flux-Quanta in Hopping Conduction,” Soviet Physics—JETP, Vol. 62, 1985, p. 1021.
  5. U. Sivan, O. Entin-Wohlman and Y. Imry, “Orbital Magnetoconductance in the Variable-Range-Hopping Regime,” Physical Review Letters, Vol. 60, No. 15, 1988, pp. 1566- 1569. doi:10.1103/PhysRevLett.60.1566
  6. J. C. Ousset, S. Askenazy, H. Rakoto and J. M. Broto, “Analytic Expressions of the Magnetoresistance Due to Localization and Electron-Electron Interaction Effects. Application to the Amorphous Alloys La3Al and La3Ga,” Journal de Physique, Vol. 46, No. 12, 1985, pp. 2145- 2149. doi:10.1051/jphys:0198500460120214500
  7. D. V. Baxter, R. Richter, M. L. Trudeau, R. W. Cochrane and J. O. Strom-Olsen, “Fitting to Magnetoresistance under Weak Localization in Three Dimensions,” Journal de Physique, Vol. 50, No. 13, 1989, pp. 1673-1688. doi:10.1051/jphys:0198900500130167300
  8. B. L. Altshuler, A. G. Aronov and D. E. Khmelnitski, “Effects of Electron-Electron Collisions with Small Energy Transfers on Quantum Localisation,” Journal of Physics C: Solid State Physics, Vol. 15, No. 36, 1982, Article ID: 7367. doi:10.1088/0022-3719/15/36/018
  9. Y. Toyozawa, “Theory of Localized Spins and Negative Magnetoresistance in the Metallic Impurity Conduction,” Journal of the Physical Society of Japan, Vol. 17, 1962, pp. 986-1004. doi:10.1143/JPSJ.17.986
  10. D. J. Bishop, E. G. Spencer and R. C. Dynes, “The Metal-Insulator Transition in Amorphous Nb:Si,” SolidState Electronics, Vol. 28, No. 1-2, 1985, pp. 73-79. doi:10.1016/0038-1101(85)90212-6
  11. N. F. Mott, “Conduction in Glasses Containing Transition Metal Ions,” Journal of Non-Crystalline Solids, Vol. 1, No. 1, 1968, pp. 1-17. doi:10.1016/0022-3093(68)90002-1
  12. N. F. Mott, “Metal-Insulator Transitions,” Taylor and Francis, London, 1974.
  13. I. S. Shlimak and E. I. Nikulin, JETP Letters, Vol. 15, 1972, p. 20.
  14. F. R. Allen and C. J. Adkins, “Electrical Conduction in Heavily Doped Germanium,” PhysicsPhilosophical Magazine, Vol. 26, No. 4, 1972, pp. 1027-1042. doi:10.1080/14786437208226974
  15. N. V. Agrinskaya and V. I. Kozub, “Effect of Preexponential Factors on Temperature Behavior of VRH Conductivity,” Solid State Communications, Vol. 91, No. 11, 1994, pp. 853-857. doi:10.1016/0038-1098(94)90001-9
  16. G. Biskupski, H. Dubois and O. Laborde, “Lecture Notes in Physics,” Springer, Berlin, 1984.
  17. B. I. Shklovskii and A. L. Efros, “Electronic Properties of Doped Semiconductors,” Springer, Berlin, 1984.
  18. A. L. Efros, and B. I. Shklovskii, “Coulomb Gap and Low Temperature Conductivity of Disordered Systems,” Journal of Physics C: Solid State Physics, Vol. 8, 1975, pp. L49-L51.
  19. T. Holstein, “Hall Effect in Impurity Conduction,” Physical Review, Vol. 124, No. 5, 1961, pp. 1329-1347. doi:10.1103/PhysRev.124.1329
  20. A. Narjis, A. El kaaouachi, L. Limouny, S. Dlimi, A. Sybous, J. Hemine, R. Abdia and G. Biskupski, “Study of Insulating Electrical Conductivity in Hydrogenated Amorphous Silicon-Nickel Alloys at Very Low Temperature,” Physica B, Vol. 406, No. 21, 2011, pp. 4155-4158. doi:10.1016/j.physb.2011.08.021
  21. H. Liu, A. Pourret and P. Guyot-Sionnest, “Mott and Efros-Shklovskii Variable Range Hopping in CdSe Quantum Dots Films,” ACS Nano, Vol. 4, No. 9, 2010, pp. 5211-5216. doi:10.1021/nn101376u
  22. V. L. Nguyen, B. Z. Spivak and B. I. Shklovskii, “Tunnel Hops in Disordered Systems,” JEPT Letters, Vol. 41, 1985, p. 42.
  23. V. L. Nguyen, B. Z. Spivak and B. I. Shklovskii, “Aharonov-Bohm Oscillations with Normal and Superconductive Flux-Quanta in Hopping Conduction,” Soviet Physics—JETP, Vol. 62, 1985, p.1021.
  24. U. Sivan, O. Entin-Wohlman and Y. Imry, “Orbital Magnetoconductance in the Variable-Range-Hopping Regime,” Physical Review Letters, Vol. 60, No. 15, 1988, pp. 1566-1569. doi:10.1103/PhysRevLett.60.1566
  25. O. Entin-Wohlman, Y. Imry and U. Sivan, “Orbital Magnetoconductance in the Variable-Range-Hopping Regime,” Physical Review B, Vol. 40, No. 12, 1989, pp. 8342-8348. doi:10.1103/PhysRevB.40.8342
  26. S. Ishida, S. Takaoka, K. Oto, K. Murase, S. Shirai and T. Serikawa, “Hopping Transport in Band-Tail of Grain Boundaries in Poly-Si TFTs,” Applied Surface Science, Vol. 113-114, 1997, pp. 685-688. doi:10.1016/S0169-4332(96)00957-9
  27. S. Shekhar, V. Prasad and S. V. Subramanyam, “Quantum Interference Effect in Strongly Localized System of Polymer-Nanocomposites,” Physics Letters A, Vol. 371, No. 5-6, 2007, pp. 486-489. doi:10.1016/j.physleta.2007.06.060
  28. W. Schirmacher, “Quantum-Interference Magnetoconductivity in the Variable-Range-Hopping Regime,” Physical Review B, Vol. 41, No. 4, 1990, pp. 2461-2468. doi:10.1103/PhysRevB.41.2461
  29. H. Fukuyama and K. Yosida, “Negative Magnetoresistance in the Anderson Localized States,” Journal of the Physical Society of Japan, Vol. 46, 1979, pp. 102-105. doi:10.1143/JPSJ.46.102
  30. K. Yosida, “Anomalous Electrical Resistivity and Magnetoresistance Due to an s-d Interaction in Cu-Mn Alloys,” Physical Review, Vol. 107, No. 2, 1957, pp. 396- 403. doi:10.1103/PhysRev.107.396
  31. B. I. Shklovskii and A. L. Efros, “Electron Properties of Doped Somiconductors,” Springer-Verlag, Berlin, 1984.
  32. A. El Kaaouachi, R. Abdia, A. Nafidi and H. Sahsah, “Variable Range Hopping Conductivity and Negative Magnetoresistance in n-Type InP Semiconductor,” Physica E, Vol. 32, No. 1-2, 2006, pp. 419-421. doi:10.1016/j.physe.2005.12.083
  33. R. Abdia, A. El Kaaouachi, A. Nafidi and J. Himine, “Positive Magnetoresistance in Hydrogenated Amorphous Alloys Silicon Nickel a-Si1-yNiy:H at Very Low Temperature with Magnetic Field,” Physica B, Vol. 373, No. 1, 2006, pp. 96-99. doi:10.1016/j.physb.2005.11.096
  34. A. El Kaaouachi, A. Nafidi, Ah. Nafidi and G. Biskupski, “Positive and Negative Magnetoresistance on Both Sides of the Metal-Insulator Transition in Metallic n-Type InP,” Semiconductor Science and Technology, Vol. 18, No. 2, 2003, p. 69. doi:10.1088/0268-1242/18/2/301
  35. A. El Kaaouachi, A. Mouden and G. Biskupski, “Negative Magnetoresistance Due to Weak Localization and Electronelectron Interactions Effects in Metallic n-Type InP Semiconductor at Very Low Temperatures with Magnetic Field,” Physica B, Vol. 266, No. 4, 1999, pp. 378- 381. doi:10.1016/S0921-4526(98)01217-4
  36. L. Essaleh, J. Galibert, S. M. Wasim, E. Hernandez and J. Leotra, “Low-Field Negative Magnetoresistance in the Variable-Range-Hopping Regime in Copper Indium Diselenide,” Physical Review B, Vol. 50, No. 24, 1994, pp. 18040-18045. doi:10.1103/PhysRevB.50.18040
  37. J. Galibert, V. A. Samuilov, V. K. Ksenevich, T. Ferrus, M. Rfailovich and J. Sokolov, “Magnetoresistance of Low Dimensional Mesoscopic Honeycomb-Shaped GaAs Networks,” Physica B, Vol. 294-295, 2001, pp. 314-318. doi:10.1016/S0921-4526(00)00667-0
  38. R. Abdia, A. El Kaaouachi, A. Nafidi and G. Biskupski, “Variable Range Hopping Conductivity and Negative Magnetoresistance in n-Type InP Semiconductor,” SolidState Electronics, Vol. 53, No. 5, 2009, pp. 469-472. doi:10.1016/j.sse.2009.02.002
  39. L. Essaleh, “Caractérisation et Étude par Magnétotransport du Composé Ternaire Semiconducteur CuInSe2,” Thèse de doctorat, Thoulouse, 1992.
  40. M. Benzaquen, D. Walsh and K. Mazuruk, “Low-Field Magnetoresistance of n-Type GaAs in the Variable-Range Hopping Regime,” Physical Review B, Vol. 38, No. 15, 1988, pp. 10933-10936. doi:10.1103/PhysRevB.38.10933
  41. G. Biskupski and H. Dubois, “Impurity Conduction and Negative Magnetoresistance in Compensated n Type Indium Phosphide, at Low Temperature,” Solid State Communications, Vol. 28, No. 8, 1978, pp. 601-605. doi:10.1016/0038-1098(78)90589-6
  42. A. Oubraham, G. Biskupski and E. Zdanowicz, “Negative Magnetoresistance of n-Type Compensated Cadmium Arsenide (CdAs2) in the Temperature Range 11 K-4.2 K,” Solid State Communications, Vol. 77, No. 5, 1991, pp. 351-354. doi:10.1016/0038-1098(91)90749-L
  43. X. D. Liu and E. Y. Jiang, “Low Temperature Magnetoresistance of Al-Doped ZnO Films,” Solid State Communications, Vol. 141, No. 7, 2007, pp. 394-397. doi:10.1016/j.ssc.2006.11.023

NOTES

*Corresponding author.

Journal Menu >>