Journal of Modern Physics
Vol.2 No.11(2011), Article ID:8627,5 pages DOI:10.4236/jmp.2011.211154
On the Quantum Statistical Distributions Describing Finite Fermions and Bosons Systems
Nuclear Physics Department, Nuclear Research Center, Atomic Energy Authority, Cairo, Egypt
E-mail: emaghraby@techemail.com
Received June 8, 2011; revised July 13, 2011; accepted July 24, 2011
Keywords: Fermion Systems, Bosons Systems, Quantum Degeneracy, Statistical Mechanics
ABSTRACT
A century old methodology for deriving statistical distribution using approximate Stirling’s formulation of the factorial becomes questionable. By avoiding the use of exaggerated approximations, a new picture of the energy distribution of fermions and bosons are presented. Energy distribution among fermions (or bosons) in systems with finite degeneracy are found to be degeneracy dependent. The presented point of view explains, successfully, presence of degeneracy pressure in ultra-cooled Fermi gas and predicts the minimum accessible temperature for finite degeneracy fermions system.
1. Introduction
Energy distribution among limited number of particles with finite degeneracy was a confusing issue when dealing with nuclear reaction/interaction. It is of the interest in pre-equilibrium reaction [1,2] in which low degeneracy states are occupied by finite number of excitons that exist together for very short time compared to the total reaction time; very long as compared to the nucleonnucleon interaction time. As a matter of quantum nature of physical system, non-degenerate and low degeneracy systems are considered finite; which means that systems from nuclei to nanoparticle are finite and their properties may be comparable. Credibility in the formulations for the asymptotic Maxwell-Boltzmann (MB), Fermi-Dirac (FD) and Bose-Einstein (BE) distribution functions guided the physicists through a century to great findings. However, modern science needs more precise expressions for these distributions [3-6]. In general, the current statistical description of the physical ensemble needs adjustment in order to follow proper justification of the definition of number and equivalence (or even non-equivalence) of a priori probabilities. One way to attain such objective is to avoid approximation. In the present work, more precise methodology is used to avoid usage of Stirling’s approximation that is used to derive the asymptotic MB, FD, and BE formulae.
2. Formulation
2.1. Dilemma of the Factorial
The explicit expression of the factorial function n! for integer value of n is given as;
 (1)
(1)
This summation is valid for any integer value of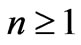 . For other non-integer values of n,
. For other non-integer values of n, ![]() function represents monotonic interpolation of the factorial function. The asymptotic behavior of the
function represents monotonic interpolation of the factorial function. The asymptotic behavior of the ![]() function with continues argument, x, is expected to follow the Stirling’s approximation;
function with continues argument, x, is expected to follow the Stirling’s approximation;
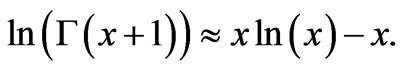 (2)
(2)
This formula fails to give acceptable representation for the range in which the argument x is small. Several other formulae are proposed [7-10] which works well as the argument approach small values. Acceptable approximation of the ![]() function is given as [10]
function is given as [10]
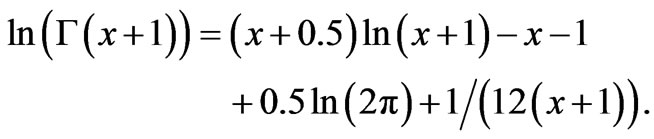 (3)
(3)
2.2. Maximum Entropy and Energy Distribution
Considering identical fermions and bosons gases in which the mutual interactions is neglected to apply extensive forms of entropy [11]. If strong correlation exists, Tsallis entropy formulation [12] may be more helpful. The number of ways that the states i is filled up with 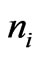 fermions is given by the Fermi-Dirac count,
fermions is given by the Fermi-Dirac count,
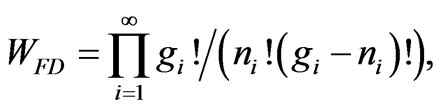 (4)
(4)
where  and
and 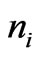 are the degeneracy and occupancy number of the level i. Similarly for Bose-Einstein count,
are the degeneracy and occupancy number of the level i. Similarly for Bose-Einstein count,
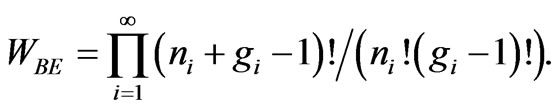 (5)
(5)
According to Boltzmann-Gibbs formalism for entropy;
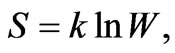 (6)
(6)
Using exact Formula (1), maximization of entropy require the differentials
 (7)
(7)
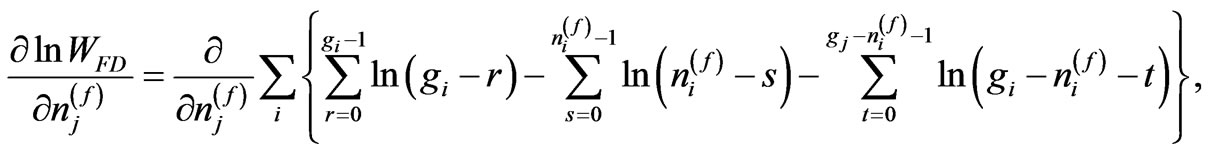 (8)
(8)
to be zero. Here, the superscripts b and f refer to bosons and fermions, respectively. The constraint of total number of particles and total energy is used to adjust the Lagrange multipliers ![]() and
and  (see [7] for details.) So,
(see [7] for details.) So,
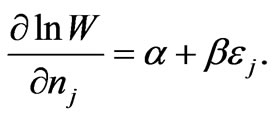 (9)
(9)
One directly reaches to the following result
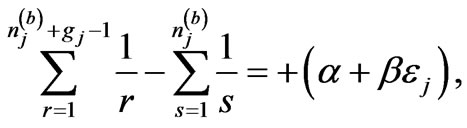 (10)
(10)
for bosons, and
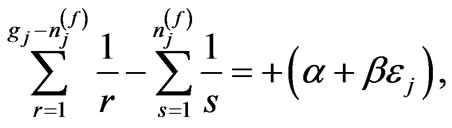 (11)
(11)
for fermions. Each of these summations represents a harmonic-number function of the form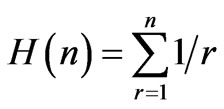 .
.
Hence, Equations (7) and (8) are reduced to:
 (12)
(12)
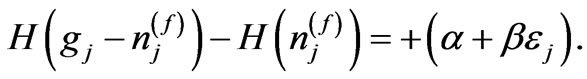 (13)
(13)
To get values of 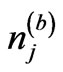 and
and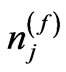 , Equations (12) and (13) are reformulated using our intention of the harmonic-number function of being approximated to a sequence including logarithmic term [13];
, Equations (12) and (13) are reformulated using our intention of the harmonic-number function of being approximated to a sequence including logarithmic term [13];
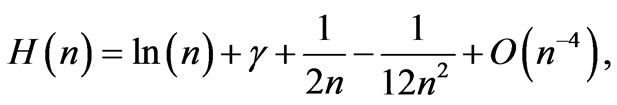 (14)
(14)
Here, 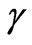 is the Euler-Mascheroni number. Adding and subtracting suitable logarithmic functions of the form
is the Euler-Mascheroni number. Adding and subtracting suitable logarithmic functions of the form  in Equation (12) and of the form
in Equation (12) and of the form  in Equation (13) shall preserve the exactness of the formulae. Equations (12) and (13) are rewritten as;
in Equation (13) shall preserve the exactness of the formulae. Equations (12) and (13) are rewritten as;
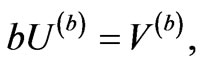 (15)
(15)
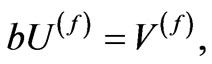 (16)
(16)
where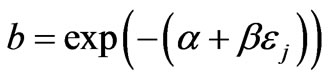 ,
, ![]() is related to the Fermi energy, and
is related to the Fermi energy, and ![]() is the energy of a state i,
is the energy of a state i,
 (17)
(17)
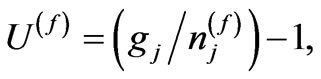 (18)
(18)
 (19)
(19)
and
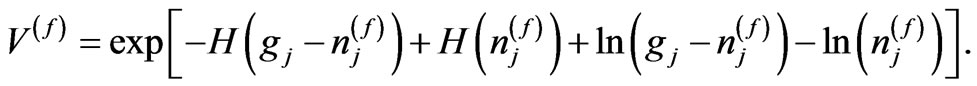 (20)
(20)
Values of the harmonic-number function are calculated by evaluation of the integration [14];
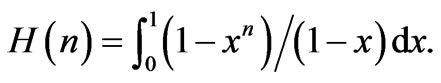 (21)
(21)
3. Results and Discussion
Equations (15) and (16) are nonlinear functions of 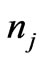 and are difficult to be solved analytically and graphical technique is used instead; the resultant distribution for fermions and bosons are given in Figure 1.
and are difficult to be solved analytically and graphical technique is used instead; the resultant distribution for fermions and bosons are given in Figure 1.
3.1. Case of Fermions
It is known that the formal FD distribution is extending to very low energy without limit. Contradiction that may appear in the present fermions-distribution may be confusing. According to the results given in Figure 1(a), the fermions-distribution (as I shall call) is degeneracy dependent. In this fermions-distribution, there are bounds for the particle energy. Let us assign the high energy bound at 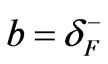 and the low energy bound at
and the low energy bound at . Some fermions low energy limits are given in Table 1 together with its associated 1-dimensional temperature in the unit of Fermi temperature.
. Some fermions low energy limits are given in Table 1 together with its associated 1-dimensional temperature in the unit of Fermi temperature.
Let us recall experiments of evaporative cooling of diluted fermions gas. The cooling process is usually mediated by bosons gas (sympathetic cooling cf. [21].) In such experiments, introduction of Zeeman splitting by

Table 1. The lower bound of accessible temperature for nondegenerate (gi = 1) and low degeneracy Fermi gas. Here ![]() is the degeneracy of the fermion state. D is the number of degree of freedoms in which the measurements are taken in and
is the degeneracy of the fermion state. D is the number of degree of freedoms in which the measurements are taken in and 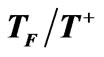 (Expec.) = 2
(Expec.) = 2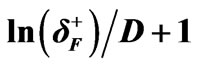 .
.
means of high magnetic field is usually done. Fermions are atoms with odd number of neutrons like 6Li and 40K while bosons are atoms with even number of neutrons like 7Li, 23Na, and 87Rb.
The degeneracy pressure prevents cooling of the fermion gas to temperature less than certain value, say 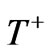 in present case. Two main techniques had been used to determine the temperature; the first is the optical density for specific wavelengths absorbed through the gas cloud [15-18] which measure the one-dimensional kinetic energy,
in present case. Two main techniques had been used to determine the temperature; the first is the optical density for specific wavelengths absorbed through the gas cloud [15-18] which measure the one-dimensional kinetic energy, . The second technique uses spatial dimension of the cloud shadows [19,20] which measure the two-dimensional kinetic energy,
. The second technique uses spatial dimension of the cloud shadows [19,20] which measure the two-dimensional kinetic energy, . The high magnetic field ensures the non-degeneracy of these states, i.e.
. The high magnetic field ensures the non-degeneracy of these states, i.e.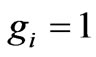 . According to my results, the lowest temperature for non-degenerate Fermi gas should be
. According to my results, the lowest temperature for non-degenerate Fermi gas should be  in one-dimensions which is equivalent to
in one-dimensions which is equivalent to 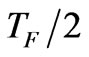 in two dimensions. These result are exactly the minimum temperature ever reached until now for non-degenerate Fermi gas, see Table 1 for comparison with experimental results.
in two dimensions. These result are exactly the minimum temperature ever reached until now for non-degenerate Fermi gas, see Table 1 for comparison with experimental results.
3.2. Case of Bosons
Similar degeneracy effect is apparent for the bosonsdistribution (as I shall call) as shown in Figure 1(b). At very low energy, the bosons-distribution coincide with the BE-distribution. Experimental evidence for the absence of low energy bound is observed during synpathetic cooling of fermions and bosons mixture. Truscott et al. [20] give definite evidence that continues to cool down. There is a certain high-energy limit for the bosons-distribution (no-solution could be found for Equations (15) and (16)), typically at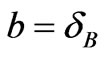 . The high energy limit of the of the bosons-distribution (
. The high energy limit of the of the bosons-distribution (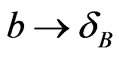 ) may give attributes of the “maximum” accessible energy for the bosons in the system.
) may give attributes of the “maximum” accessible energy for the bosons in the system.
The limitations ,
, 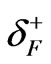 , and
, and 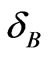 can be estimated for a good approximation by applying the principle of maximum entropy and Lagrange multipliers technique using Equation (3). One gets directly the most probable distribution in energy;
can be estimated for a good approximation by applying the principle of maximum entropy and Lagrange multipliers technique using Equation (3). One gets directly the most probable distribution in energy;
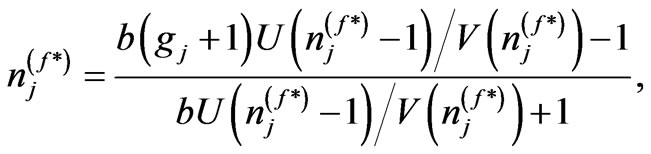 (22)
(22)
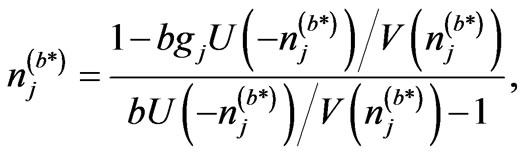 (23)
(23)
for fermions and bosons, respectively. Here,
 (24)
(24)
 (a)
(a)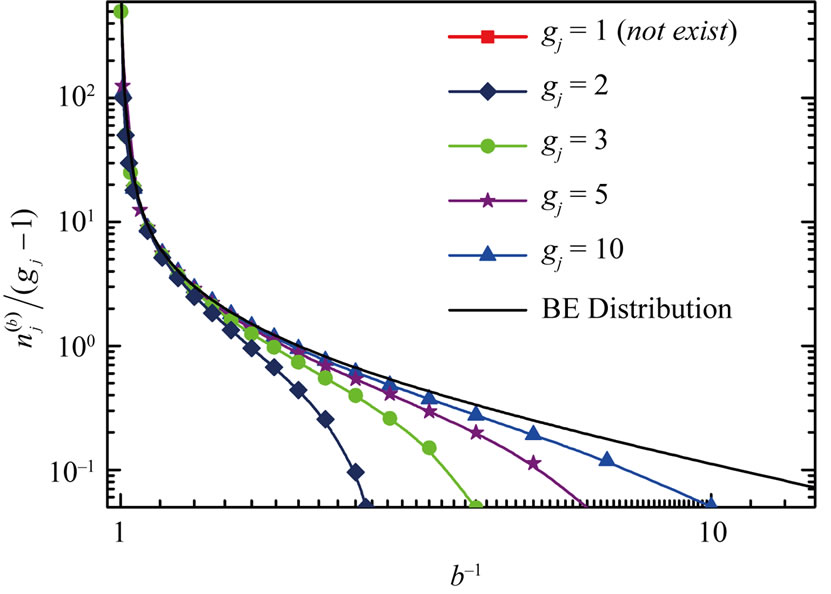 (b)
(b)
Figure 1. Connected symbols refer to graphical solutions of Equations (15) and (16) (a) for fermions and (b) for bosons; while for the FD and BE distributions are represented by solid line without symbols. In part (a), the intersections with the horizontal axis at 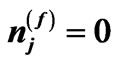 and 1 give the reciprocal values of
and 1 give the reciprocal values of  and
and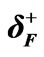 , respectively. In part (b) the intersection with the horizontal axis in which
, respectively. In part (b) the intersection with the horizontal axis in which 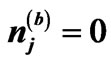 (not shown in logarithmic scale) gives the reciprocal value of
(not shown in logarithmic scale) gives the reciprocal value of .
.
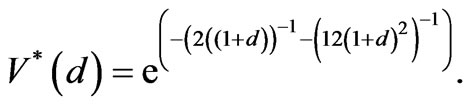 (25)
(25)
The asterisk indicates that the variables are derived using approximation 3. The limits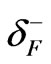 ,
, 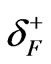 , and
, and 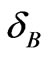 that satisfies Equations (22) and (23) is obtained by giving
that satisfies Equations (22) and (23) is obtained by giving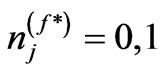 , and
, and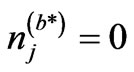 , respectively. That is;
, respectively. That is;
 (26)
(26)
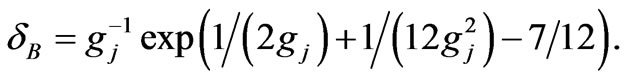 (27)
(27)
which satisfies the equality . As the value of
. As the value of  increases, the value of
increases, the value of 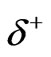 increases. Hence, highly degenerate Fermi system should follow FD distribution.
increases. Hence, highly degenerate Fermi system should follow FD distribution.
4. Conclusions
The applicability of the formal FD and BE statistical distributions become questionable in finite systems of small degeneracy in spite of its success in describing common physical system. More precise quantum distribution functions need to be used if the degeneracy of the state of the system is low. If a system of fermions gas is considered, there is a minimum temperature limit that the system cannot encroach upon, without violation of Pauli Exclusion Principle.
REFERENCES
- E. K. Elmaghraby, “Initial Exciton Configuration in (p,n) Pre-Equilibrium Emission Reactions,” Physical Review C, Vol. 78, 2008, Article ID 014601. doi:10.1103/PhysRevC.78.014601
- E. K. Elmaghraby, “PHASE-OTI: A Pre-Equilibrium Model Code for Nuclear Reactions Calculations,” Computer Physics Communications, Vol. 180, 2009, pp. 1694- 1699. doi:10.1016/j.cpc.2009.03.015
- R. K. Niven, “Exact Maxwell-Boltzmann, Bose-Einstein and Fermi-Dirac statistics,” Physics Letters A, Vol. 342, No. 4, 2005, pp. 286-293. doi:10.1016/j.physleta.2005.05.063
- R. K. Niven, “Non-Asymptotic Thermodynamic Ensembles,” Europhysics Letters, Vol. 86, 2009, p. 20010. doi:10.1209/0295-5075/86/20010
- R. K. Niven, “Cost of s-Fold Decisions in Exact Maxwell Boltzmann, Bose Einstein and Fermi Dirac Statistics, Physica A, Vol. 365, No. 1, 2006, pp. 142-149. doi:10.1016/j.physa.2006.01.021
- C. Tsallis, “Nonadditive Entropy: The Concept and Its Use,” European Physical Journal A, Vol. 40, No. 3, 2009, pp. 257-266. doi:10.1140/epja/i2009-10799-0
- A. Isihara, “Statistical Physics,” Academic Press, New York, 1971.
- Y. Weissman, “An Improved Analytical Approximation to n!,” American Journal of Physics, Vol. 51, No. 1, 1983, p. 9. doi:10.1119/1.13412
- N. D. Mermin, “Improving an Improved Analytical Approximation to n!,” American Journal of Physics, Vol. 51, No. 9, 1983, p. 776. doi:10.1119/1.13139
- C. Leubner, “Generalised Stirling Approximations to n!,” European Journal of Physics, Vol. 6, 1985, pp. 299-301. doi:10.1088/0143-0807/6/4/016
- C. Tsallis and U. Tirnakli, “Nonadditive Entropy and Nonextensive Statistical Mechanics—Some Central Concepts and Recent Applications,” Journal of Physics: Conference Series, Vol. 201, No. 1, 2010, Article ID 012001.
- C. Tsallis, “Possible generalization of Boltzmann-Gibbs Statistics,” Journal of Statistical Physics, Vol. 52, No. 1-2, 1988, pp. 479-487. doi:10.1007/BF01016429
- B.-N. Guo and F. Qi, “Sharp Bounds for Harmonic Numbers,” Applied Mathematics and Computing, 2011, Article in Press.
- A. Sofo, “Integral Forms of Sums Associated with Harmonic Numbers,” Applied Mathematics and Computing, Vol. 207, No. 2, 2009, pp. 365-372. doi:10.1016/j.amc.2008.10.044
- F. Schreck, L. Khaykovich, K. L. Corwin, G. Ferrari, T. Bourdel, J. Cubizolles and C. Salomon, “Quasipure BoseEinstein Condensate Immersed in a Fermi Sea,” Physical Review Letters, Vol. 87, No. 8, 2001, Article ID 080403. doi:10.1103/PhysRevLett.87.080403
- Z. Hadzibabic, S. Gupta, C. A. Stan, C. H. Schunck, M. W. Zwierlein, K. Dieckmann and W. Ketterle, “Fiftyfold Improvement in the Number of Quantum Degenerate Fermionic Atoms,” Physical Review Letters, Vol. 91, No. 16, 2003, Article ID 160401. doi:10.1103/PhysRevLett.91.160401
- S. Gupta, Z. Hadzibabic, M. W. Zwierlein, C. A. Stan, K. Dieckmann, C. H. Schunck, E. G. M. van Kempen, B. J. Verhaar and W. Ketterle, “Radio-Frequency Spectroscopy of Ultracold Fermions,” Science, Vol. 300, No. 5626, 2003, pp. 1723-1726. doi:10.1126/science.1085335
- S. Aubin, S. Myrskog, M. H. T. Extavour, L. J. Leblanc, D. McKay, A. Stummer and J. H. Thywissen, “Rapid Sympathetic Cooling to Fermi Degeneracy on a Chip,” Nature Physics, Vol. 2, No. 6, 2006, pp. 384-387. doi:10.1038/nphys309
- B. DeMarco and D. S. Jin, “Onset of Fermi Degeneracy in a Trapped Atomic Gas,” Science, Vol. 285, No. 5434, 1999, pp. 1703-1706. doi:10.1126/science.285.5434.1703
- A. G. Truscott, K. E. Strecker, W. I. McAlexander, G. B. Partridge and R. G. Hulet, “Observation of Fermi Pressure in a Gas of Trapped Atoms,” Science, Vol. 291, No. 5513, 2001, pp. 2570-2572. doi:10.1126/science.1059318
- C. J. Myatt, E. A. Burt, R. W. Ghrist, E. A. Cornell and C. E. Wieman, “Production of Two Overlapping Bose-Einstein Condensates by Sympathetic Cooling,” Physical Review Letters, Vol. 78, No. 4, 1997, pp. 586-589. doi:10.1103/PhysRevLett.78.586

