Journal of Modern Physics
Vol.2 No.12(2011), Article ID:16501,7 pages DOI:10.4236/jmp.2011.212177
Why the Big Bang Model Cannot Describe the Observed Universe Having Pressure and Radiation
Theoretical Astrophysics Section, Bhabha Atomic Research Centre, Mumbai, India
E-mail: amitra@barc.gov.in
Received July 27, 2011; revised October 8, 2011; accepted October 25, 2011
Keywords: General Relativity, Big Bang Model, Dark Energy, Cosmology, Fractal Universe
ABSTRACT
It has been recently shown that, since in general relativity (GR), given one time label t, one can choose any other time label t → t* = f(t), the pressure of a homogeneous and isotropic fluid is intrinsically zero (Mitra, Astrophys. Sp. Sc. 333, 351, 2011). Here we explore the physical reasons for the inevitability of this mathematical result. The essential reason is that the Weyl Postulate assumes that the test particles in a homogeneous and isotropic spacetime undergo pure geodesic motion without any collisions amongst themselves. Such an assumed absence of collisions corresponds to the absence of any intrinsic pressure. Accordingly, the “Big Bang Model” (BBM) which assumes that the cosmic fluid is not only continuous but also homogeneous and isotropic intrinsically corresponds to zero pressure and hence zero temperature. It can be seen that this result also follows from the relevant general relativistic first law of thermodynamics (Mitra, Found. Phys. 41, 1454, 2011). Therefore, the ideal BBM cannot describe the physical universe having pressure, temperature and radiation. Consequently, the physical universe may comprise matter distributed in discrete non-continuous lumpy fashion (as observed) rather than in the form of a homogeneous continuous fluid. The intrinsic absence of pressure in the “Big Bang Model” also rules out the concept of a “Dark Energy”.
1. Introduction
In general relativity (GR), one is supposed to obtain the spacetime geometry 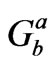 by using the matter energy momentum tensor (EMT)
by using the matter energy momentum tensor (EMT) 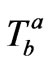 warping the spacetime:
warping the spacetime: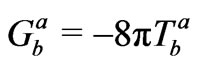 . This means that the components of the metric tensor
. This means that the components of the metric tensor  depend on the components of matter EMT. And if the spacetime is isotropic and homogeneous, some component of
depend on the components of matter EMT. And if the spacetime is isotropic and homogeneous, some component of 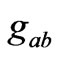 may depend solely on appropriate components of EMT and not on coordinates. An isotropic and homogeneous spacetime is necessarily spherically symmetric about any point and the general form of a spherically symmetrical metric in comoving coordinates
may depend solely on appropriate components of EMT and not on coordinates. An isotropic and homogeneous spacetime is necessarily spherically symmetric about any point and the general form of a spherically symmetrical metric in comoving coordinates 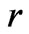 and
and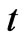 :
:
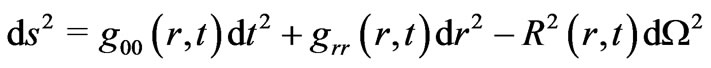 (1)
(1)
where 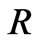 is the area coordinate and
is the area coordinate and 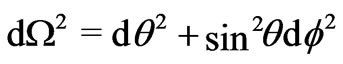 . In the comoving frame, the components of the energy momentum tensor of the perfect fluid are (
. In the comoving frame, the components of the energy momentum tensor of the perfect fluid are (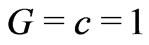 ):
):
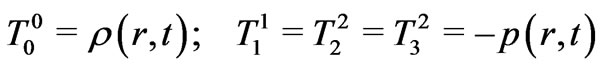 (2)
(2)
At the same time GR obeying “general covariance" or “Diffeomorphism Covariance”, offers use of arbitrary coordinates. This is so because, in Nature, coordinates do not exist a priori, and hence should play no role in the formulation of fundamental physical laws. One of the basic applications of this principle is that given one time label , one is free to choose an arbitrary new time label
, one is free to choose an arbitrary new time label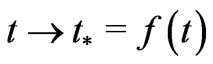 , without any loss of generality. Consequently, given one form of
, without any loss of generality. Consequently, given one form of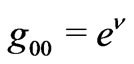 , one can have infinite forms of
, one can have infinite forms of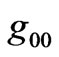 . But
. But 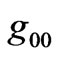 s do depend on
s do depend on 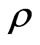 and
and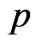 . Therefore “Diffeomorphism Covariance” may impose conditions on the admissible intrinsic forms of
. Therefore “Diffeomorphism Covariance” may impose conditions on the admissible intrinsic forms of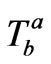 . To appreciate this subtle point further, let us invert the Einstein equation:
. To appreciate this subtle point further, let us invert the Einstein equation:
 (3)
(3)
Thus when one imposes some conditions on 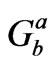 by assuming certain spacetime symmetry, one unmindfully imposes constraint on the admissible forms of
by assuming certain spacetime symmetry, one unmindfully imposes constraint on the admissible forms of 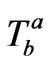 too. Many GR solutions however have not been analyzed from such considerations though this line of argument can throw important physical insights into the inherent physical constraints. For instance consider the problem of the adiabatic gravitational collapse of a homogeneous sphere apparently having an isotropic pressure
too. Many GR solutions however have not been analyzed from such considerations though this line of argument can throw important physical insights into the inherent physical constraints. For instance consider the problem of the adiabatic gravitational collapse of a homogeneous sphere apparently having an isotropic pressure 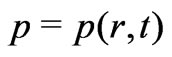 . This problem was first discussed in 1945 and since then scores of authors have worked on this problem and innumerable exact solutions have been obtained [1]. Thus even though some of the noted GR experts such as W.B. Bonnor, G.C. McVittie, H. Bondi, A. Taub and H. Nariai have suggested many solutions for this basic physical problem, appropriate application of coordinate freedom of choosing the time label has shown that, a homogeneous sphere with a pressure gradient and a boundary cannot contract or expand at all [1]. Consequently, all those relevant exact solutions are fallacious and they must correspond to zero density. And this result, obtained by appropriate application of “Diffeomorphism Covariance” can be explained on physical grounds too:
. This problem was first discussed in 1945 and since then scores of authors have worked on this problem and innumerable exact solutions have been obtained [1]. Thus even though some of the noted GR experts such as W.B. Bonnor, G.C. McVittie, H. Bondi, A. Taub and H. Nariai have suggested many solutions for this basic physical problem, appropriate application of coordinate freedom of choosing the time label has shown that, a homogeneous sphere with a pressure gradient and a boundary cannot contract or expand at all [1]. Consequently, all those relevant exact solutions are fallacious and they must correspond to zero density. And this result, obtained by appropriate application of “Diffeomorphism Covariance” can be explained on physical grounds too:
• This result may suggest that self-gravity has a natural tendency to generate not only pressure gradient but density gradient too (despite the occurrences of “exact solutions” to the contrary). It may be noted here that even for a supposed static self-gravitating sphere of uniform density, the “uniform density” should correspond to none other than 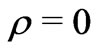 [2].
[2].
• This result may be also pointing to the fact that physical gravitational collapse/expansion must be radiative and non-adiabatic whether one is considering Newtonian gravity or GR [3].
To further appreciate the fact how some of the exact solutions could be physically misleading, recall the case of the celebrated Oppenheimer-Snyder solution which has been considered as the ultimate proof that GR allows formation of “Black Holes” (BH). But now it has been shown that, this solution is only a mathematical illusion, it does not really imply any BH/singularity formation because a strict 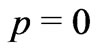 fluid has
fluid has 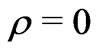 too [4].
too [4].
Similarly, by using this coordinate freedom of choosing time coordinate in GR and by directly integrating the part of the local energy momentum conservation equation:
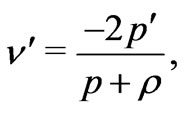 (4)
(4)
where a prime denotes differentiation by , it was found that, for the Big Bang Model (BBM) one can express [5]
, it was found that, for the Big Bang Model (BBM) one can express [5]
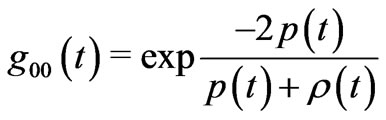 (5)
(5)
This result seems to be justified because, after all, 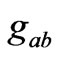 is determined by
is determined by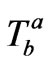 . But by the coordinate freedom of choosing arbitrary time label without making any compromise on the physical content of the problem, one can choose a new time label in which
. But by the coordinate freedom of choosing arbitrary time label without making any compromise on the physical content of the problem, one can choose a new time label in which
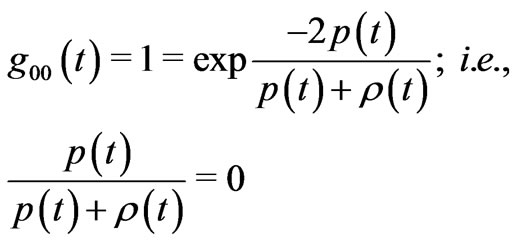 (6)
(6)
Since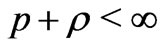 , this result means that,
, this result means that,
 (7)
(7)
But pressure is a scalar and must remain unaltered by coordinate relabelling. Therefore, for the BBM model, one must intrinsically have . The result is suggesting that self-gravity manisfests itself through the pressure gradient, and the latter can vanish only when pressure itself vanishes.
. The result is suggesting that self-gravity manisfests itself through the pressure gradient, and the latter can vanish only when pressure itself vanishes.
Even if it would transpire that 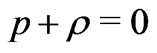 too, this result need not change because a
too, this result need not change because a 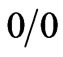 form can be anything including 0.
form can be anything including 0.
2. Physical Reasons
Weyl’s postulate demands that an isotropic and homogeneous spacetime metric is diagonal like (1). Since there cannot be any pressure gradient for the fluid residing in this spacetime, it follows that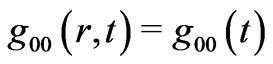 . While this fact is used by many authors, nobody ever made any serious attempt to determine the EMT dependence of
. While this fact is used by many authors, nobody ever made any serious attempt to determine the EMT dependence of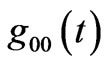 . At the most, some authors justify the
. At the most, some authors justify the 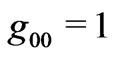 result by considering the cosmic fluid as pressureless “Dust” on the ground that Weyl’s postulate implies no collision amongst the test particles. On the other hand, some authors just use the fact that once
result by considering the cosmic fluid as pressureless “Dust” on the ground that Weyl’s postulate implies no collision amongst the test particles. On the other hand, some authors just use the fact that once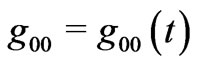 , one can set
, one can set 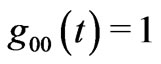 in a new time label. Alternately, some authors directly invoke Weyl’s postulate which implies the existence of an universal Newtonian like cosmic time and set
in a new time label. Alternately, some authors directly invoke Weyl’s postulate which implies the existence of an universal Newtonian like cosmic time and set 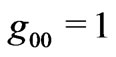 in order to obtain the Friedmann Robertson Walker (FRW) metric.
in order to obtain the Friedmann Robertson Walker (FRW) metric.
For instance, in p. 322, Schutz admits [6] that
“Each galaxy is idealized as having no random velocity...”, i.e., he admits that he assumes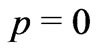 . Next he writes “The time coordinate
. Next he writes “The time coordinate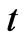 , the proper time of each galaxy”, i.e., he considers
, the proper time of each galaxy”, i.e., he considers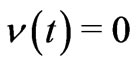 , and this is indeed correct for
, and this is indeed correct for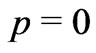 . But having derived the metric by assuming
. But having derived the metric by assuming , in p. 324, he adds [6] that “We idealize the universe as filled with a perfect fluid having
, in p. 324, he adds [6] that “We idealize the universe as filled with a perfect fluid having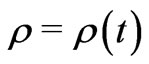 ,
, 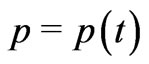 etc.” And then he proceeds to Big-Bang Model having
etc.” And then he proceeds to Big-Bang Model having ! Clearly, Schutz first obtained the metric by assuming
! Clearly, Schutz first obtained the metric by assuming 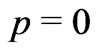 and then extrapolated it to the
and then extrapolated it to the 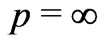 situation!
situation!
Similarly, in p.130, Narlikar admits [7]:
“In our smooth-fluid approximation a velocity field like  represents an orderly motion with no pressure. Thus we have in this case a system of galaxies behaving like dust with
represents an orderly motion with no pressure. Thus we have in this case a system of galaxies behaving like dust with .”
.”
And he attempts to justify the application of this dust model to physical universe by noting that, in the present epoch, 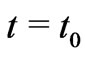 , we have
, we have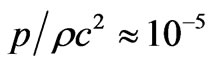 . But he admits that even if the fluid would be assumed as dust at present epoch, it must not be assumed so in early epochs:
. But he admits that even if the fluid would be assumed as dust at present epoch, it must not be assumed so in early epochs:
“we have to abandon our simplified picture of cosmology ....” [7].
But has any author ever abandoned this “simplified picture” for high pressure early epochs? No! The same FRW metric derived by implicitly assuming a dust picture has been used by all for situations with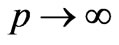 . Further, the definition of a “Dust” is not a fluid which has
. Further, the definition of a “Dust” is not a fluid which has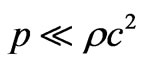 ; on the other hand, the definition of a `Dust’ is a fluid having
; on the other hand, the definition of a `Dust’ is a fluid having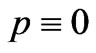 . In fact the condition
. In fact the condition  only referes to a fluid which is non-relativistic but not a dust, just like ordinary stars or water in the oceans.
only referes to a fluid which is non-relativistic but not a dust, just like ordinary stars or water in the oceans.
Now let us try to appreciate the inevitability of this  result from various other physical considerations too.
result from various other physical considerations too.
If a fluid has 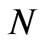 molecules, in the presence of mutual collisions and pressure, the motion of the
molecules, in the presence of mutual collisions and pressure, the motion of the 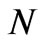 particles get overlapped and smeared. Then one really cannot indentify the motion of any “individual” moelcule. And in the presence of collisions, there is no question of conservation of energy of an individual molecule even if the interaction would be conservative. But in the FRW model one has
particles get overlapped and smeared. Then one really cannot indentify the motion of any “individual” moelcule. And in the presence of collisions, there is no question of conservation of energy of an individual molecule even if the interaction would be conservative. But in the FRW model one has
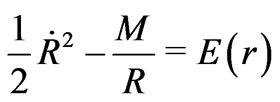 (8)
(8)
This Equation suggests that with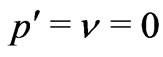 , the complex
, the complex  body problem gets split into
body problem gets split into 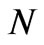 1-body problems where energy of each molecule is strictly conserved
1-body problems where energy of each molecule is strictly conserved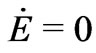 ! This suggests that the assumption of
! This suggests that the assumption of 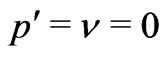 also means there is no collision, no pressure. Further, with
also means there is no collision, no pressure. Further, with  assumption, the problem acquires a pure Newtonian dust character too. And this is the reason why FRW cosmology can be derived from purely Newtonian physics [7]! While, mathematically, Weyl’s postulate merely suggests
assumption, the problem acquires a pure Newtonian dust character too. And this is the reason why FRW cosmology can be derived from purely Newtonian physics [7]! While, mathematically, Weyl’s postulate merely suggests 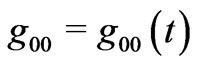 [7], physically, it suggests streamlined motion with no randomness, no collision [7]. Thus eventually Weyl’s postulate suggests pure geodesic motion with
[7], physically, it suggests streamlined motion with no randomness, no collision [7]. Thus eventually Weyl’s postulate suggests pure geodesic motion with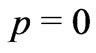 .
.
For a degenerate quantum fluid near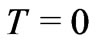 , the pressure arises due to zero point vibrations around fixed mean locations. In such a case, despite the presence of pressure, one may identify a given molecule at a given fixed
, the pressure arises due to zero point vibrations around fixed mean locations. In such a case, despite the presence of pressure, one may identify a given molecule at a given fixed . But, note, here we are considering a pressure of purely kinetic origin where “molecules” are free to roam around anywhere unless the system has a natural boundary. Even if a natural boundary/wall would be there, a given molecule say, “Andromeda”, could be anywhere within that boundary. In such a case, one cannot ascribe any fixed coordinate
. But, note, here we are considering a pressure of purely kinetic origin where “molecules” are free to roam around anywhere unless the system has a natural boundary. Even if a natural boundary/wall would be there, a given molecule say, “Andromeda”, could be anywhere within that boundary. In such a case, one cannot ascribe any fixed coordinate 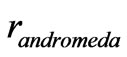 to Andromeda. Even if one would consider the famous analogy of raisins stuck in a puffing up cake, the raisins are not free to roam around within the cake. In otherwords, the fluid comprising the raisins has no pressure, no random motion. However, if the motion of the raisins would be sufficiently random, the shifts in spectral lines emitted by them need not obey Hubble’s law. In fact there could be blue shifts as well even if the background cake would always be inflating. A little introspection would show that, if the raisins would indeed be vigorously colliding amongst themselves, the basic analogy of a puffing up cake would break down. On the other hand, such an analogy is really valid only when the raisins are not at all colliding.
to Andromeda. Even if one would consider the famous analogy of raisins stuck in a puffing up cake, the raisins are not free to roam around within the cake. In otherwords, the fluid comprising the raisins has no pressure, no random motion. However, if the motion of the raisins would be sufficiently random, the shifts in spectral lines emitted by them need not obey Hubble’s law. In fact there could be blue shifts as well even if the background cake would always be inflating. A little introspection would show that, if the raisins would indeed be vigorously colliding amongst themselves, the basic analogy of a puffing up cake would break down. On the other hand, such an analogy is really valid only when the raisins are not at all colliding.
3. First Law of Thermodynamics & BBM
For a spherically symmetrical fluid, the best measure of total mass energy content in a given section is given by the so-called “Misner-Sharp” mass [9,10]:
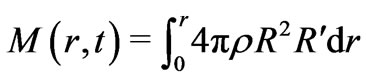 (9)
(9)
The adiabatically evolving fluid obeys the following equation
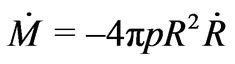 (10)
(10)
where an overdot denotes differentiation by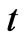 . This shows that, the mass-energy content in a given section of the fluid is not conserved if indeed
. This shows that, the mass-energy content in a given section of the fluid is not conserved if indeed . For an isolated star with a boundary, however, the total massenergy would be conserved because at the boundary with
. For an isolated star with a boundary, however, the total massenergy would be conserved because at the boundary with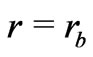 , one has
, one has . But for the universe, there can not be any such edge, and the principle of energy conservation is violated.
. But for the universe, there can not be any such edge, and the principle of energy conservation is violated.
Accordingly Harrison wondered [8]:
“The total energy decreases in an expanding universe. Where does the energy go in an expanding universe?”
And naturally he concluded that “energy of the universe is not conserved”.
But before this he noted that [8]:
“The universe is not in the least like a steam engine and we must never jump to the conclusion that pressure is the cause of expansion. Pressure has nothing to with why universe expands. the universe could just as well contract...
If the universe possesses a cosmic edge, the situation would be different; the pressure at the edge could then do work, and we would have a universe similar to a steam engine. But the universe has no edge, and the pressure everywhere is impotent to produce mechanical energy.”
But if for the edgeless FRW universe, pressure is impotent to produce mechanical energy, why would 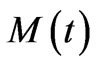 change at all? It is not difficult to see that all such self-contradictions result from the mistake of assuming
change at all? It is not difficult to see that all such self-contradictions result from the mistake of assuming 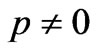 for a flow which is actually geodesic.
for a flow which is actually geodesic.
Further, for any spherically symmetric spacetime, one can define a mass-energy current [10]
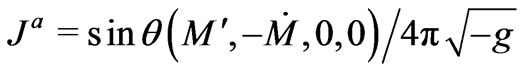 (11)
(11)
where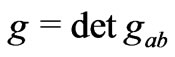 . And the conservation of
. And the conservation of 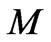 immediately follows from the fact that [10]
immediately follows from the fact that [10]
 (12)
(12)
The radial component of this current 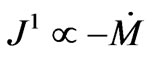 can involve both radiation flux and mechanical
can involve both radiation flux and mechanical 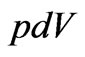 flux. For a homogeneous and isotropic spacetime, having no inward or outward direction, there cannot be any net radial current of mass-energy. And this is the reason that there cannot be any net heat/radiation flow in such a spacetime. But even in the absence of heat flow, there would be a current of mechanical energy flow and which too must be zero:
flux. For a homogeneous and isotropic spacetime, having no inward or outward direction, there cannot be any net radial current of mass-energy. And this is the reason that there cannot be any net heat/radiation flow in such a spacetime. But even in the absence of heat flow, there would be a current of mechanical energy flow and which too must be zero:
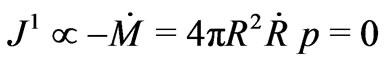 (13)
(13)
Therefore either the FRW universe should be static with 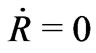 or possess no pressure.
or possess no pressure.
3.1. Independent Proof
Note, Equation (10) may be also written as
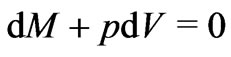 (14)
(14)
where
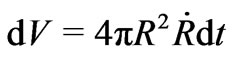 (15)
(15)
is the coordinate volume element swept by a given mass shell at a fixed . For the FRW metric
. For the FRW metric
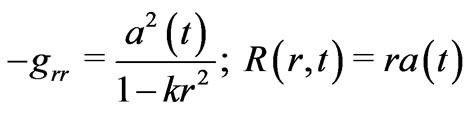 (16)
(16)
where 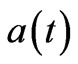 is the scale factor. And the proper volume element corresponding to
is the scale factor. And the proper volume element corresponding to  is
is
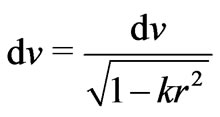 (17)
(17)
In GR, proper volume element rather than coordinate volume element has physical significance. Thus the 1st law of thermodynamics should involve proper volume element rather than coordinate volume element; and hence, for an adiabatically evolving fluid, one should have [11]
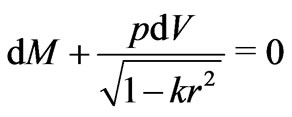 (18)
(18)
Equations (14) and (18) are compatible to each other only when either 1) 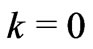 or 2) in a general case,
or 2) in a general case,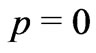 . This again strongly suggests that
. This again strongly suggests that 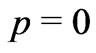 for the BBM.
for the BBM.
3.2. Yet Another Confirmation
For a spherically symmetrical homogeneous dust, one can work out the 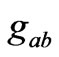 s by explicitly solving the Einstein equations:
s by explicitly solving the Einstein equations:
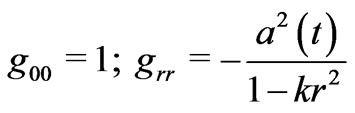 (19)
(19)
But the FRW metric too has exactly the same 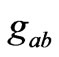 s (the angular part is obviously the same); i.e.,
s (the angular part is obviously the same); i.e.,
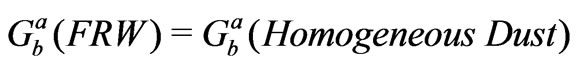 (20)
(20)
Then by Einstein Equation (3), one should have
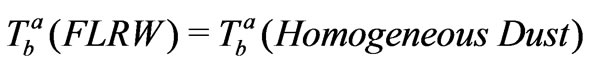 (21)
(21)
But we know that,
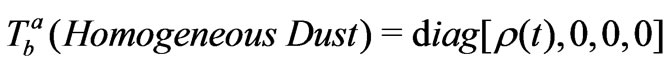 (22)
(22)
Therefore we should have
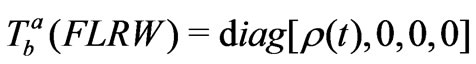 (23)
(23)
And Equation (7) precisely denotes this fact.
4. More on Energy Conservation
Baryshev [12] and many others have opined that BBM violates the principle of energy conservation.
Also, Peebles [13] noted that constant loss of energy by photons in an expanding universe appears to violate conservation of energy: “The resolution of this apparent paradox is that while energy conservation is a good local concept, ... there is not a general global conservation in general relativity”.
This is incorrect, actually, GR too has global energy conservation principle after one would account for gravitational field energy  and self-gravitational interaction energy. The effect of (negative) self-gravitation is manifest through the presence of gravitational red-shift, i.e.,
and self-gravitational interaction energy. The effect of (negative) self-gravitation is manifest through the presence of gravitational red-shift, i.e.,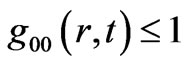 . But once one would set
. But once one would set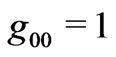 , gravitational red-shift and negative self-gravitation should vanish [14]. And by using appropriate super-potentials, Rosen found that total energy of FRW universe is
, gravitational red-shift and negative self-gravitation should vanish [14]. And by using appropriate super-potentials, Rosen found that total energy of FRW universe is  [15]. It may be also found that
[15]. It may be also found that 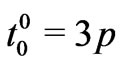 , and vanishing of total energy should imply
, and vanishing of total energy should imply 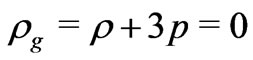 [14]. Under the assumption that both
[14]. Under the assumption that both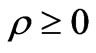 ,
,  , one should then expect that, for the BBM, not only
, one should then expect that, for the BBM, not only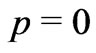 , but
, but 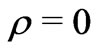 too. As already mentioned, Misner-Sharp Mass gives the best measure of quasi-local energy of an spherically symmetric fluid [9,10]. And since the universe has no edge, it is justified to equate mass energy
too. As already mentioned, Misner-Sharp Mass gives the best measure of quasi-local energy of an spherically symmetric fluid [9,10]. And since the universe has no edge, it is justified to equate mass energy 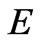 obtained by Rosen with
obtained by Rosen with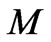 ;
;
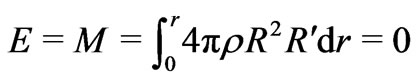 (24)
(24)
Thus it would follow that, the BBM may actually refer to a vaccum with not only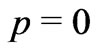 , but also
, but also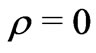 . To explore this question, we found out total energy of the Big Bang Universe in a manner more direct [16] than that of Rosen. And we found that, in order that, energy is conserved, one must have
. To explore this question, we found out total energy of the Big Bang Universe in a manner more direct [16] than that of Rosen. And we found that, in order that, energy is conserved, one must have
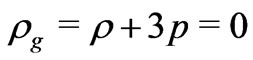 (25)
(25)
Now, if one would introduce a cosmological constant 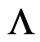 into the problem, all one needs to do is to set
into the problem, all one needs to do is to set
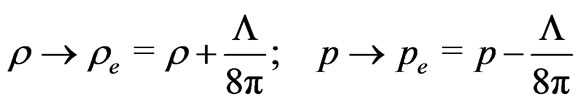 (26)
(26)
Similarly now, one should also replace
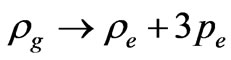 (27)
(27)
5. Dark Energy
It is believed that the observed universe could be in a state of accelerated expansion. And this is usually explained in terms of a negative 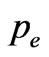 in the following (incorrect) FRW dynamic Equation:
in the following (incorrect) FRW dynamic Equation:
 (28)
(28)
And the concept of a “Dark Energy” arises from the possibility of having a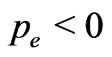 . But since, we have found that
. But since, we have found that , there cannot be any “Dark Energy”. Consequently, the FRW model always gives deceleration, and the observed acceleration cannot be explained by FRW model. It is also believed that there should be an early super hot past for the real universe in order to explain formation of light elements as well as the observed microwave background radiation. But as far as FRW, model is concerned,
, there cannot be any “Dark Energy”. Consequently, the FRW model always gives deceleration, and the observed acceleration cannot be explained by FRW model. It is also believed that there should be an early super hot past for the real universe in order to explain formation of light elements as well as the observed microwave background radiation. But as far as FRW, model is concerned,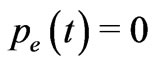 . Therefore, the temperature of the FRW fluid,
. Therefore, the temperature of the FRW fluid, . Hence FRW model cannot explain any primordial nucleosynthesis or microwave background radiation. In fact, since
. Hence FRW model cannot explain any primordial nucleosynthesis or microwave background radiation. In fact, since , FRW model cannot explain the origin of any starlight or any other radiation found in the patch of the real universe in which we live.
, FRW model cannot explain the origin of any starlight or any other radiation found in the patch of the real universe in which we live.
Further, even if we would forget radiation, or any early history, cosmic fluid must possess pressure or random motion in order to explain peculiar motions. Obviously a strict  fluid is unfit to describe any aspect of the observed universe. One may question now, then, how one would explain the physical universe. And that is very much an open and unexplained question. May be the real universe is too complex for text book type modeling. May be real universe has a complicated infinite hierarchial fractal structure which defies a smooth fluid approximation.
fluid is unfit to describe any aspect of the observed universe. One may question now, then, how one would explain the physical universe. And that is very much an open and unexplained question. May be the real universe is too complex for text book type modeling. May be real universe has a complicated infinite hierarchial fractal structure which defies a smooth fluid approximation.
To recap, in FRW metric, the gravitational potential 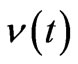 is set to zero by vitrue of the coordinate freedom in choosing an arbitrary time label for
is set to zero by vitrue of the coordinate freedom in choosing an arbitrary time label for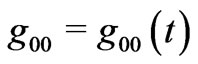 . The same coordinate freedom is seen to fix
. The same coordinate freedom is seen to fix 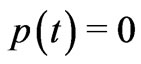 too. In case, the reader will not be sufficiently aware of this coordinate freedom, the result obtained here may appear to be spurious. But actually it is not so. Essentially, this coordinate freedom affects both sides of the Einstein Equation (Equation (3)) and ensures similar result. If
too. In case, the reader will not be sufficiently aware of this coordinate freedom, the result obtained here may appear to be spurious. But actually it is not so. Essentially, this coordinate freedom affects both sides of the Einstein Equation (Equation (3)) and ensures similar result. If 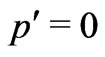 when
when , it it seems logical that
, it it seems logical that 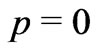 when
when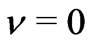 .
.
Again note, after all, by assumption, the test particles of the FRW fluid strictly obey Weyl’s postulate which asserts that the test particles are following streamlined geodesic motion without any randomness and collision. Thus, by very assumption, the FRW fluid is pressureless not just at a given epoch but at all epochs. Note, though Equation (8) tells that the energy of each particle is strictly conserved, in the faulty FRW model, energy of the fluid is not conserved! Obviously strict conservation of energy of an individual particle is possible only when there is no collision and energy exchange, i.e., no pressure. And the faulty FRW model naturally finds violation of energy conservation as it ascribes pressure for this dusty fluid.
6. Why Λ = 0 for BBM
Long back Kriele showed that there cannot be any trapped surface for a spherically symmetric homogeneous perfect fluid [17]. This seems to be a special case of the no trapped surface theorem obtained by demanding that timelike worldlines associated with material particles must always remain time like [18], i.e.,
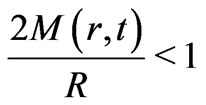 (29)
(29)
For the FRW case, one has 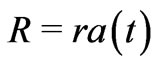 and
and
 (30)
(30)
so that one should have
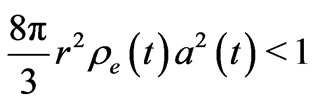 (31)
(31)
And in order that 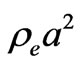 does not blow up either in future or past, one needs to have
does not blow up either in future or past, one needs to have
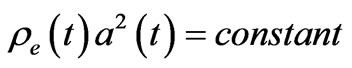 (32)
(32)
Again for this, first, it is necessary that 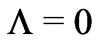 and
and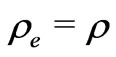 :
:
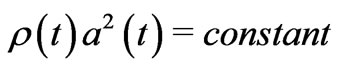 (33)
(33)
But the FRW model generally obeys  so that one should have
so that one should have
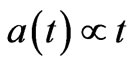 (34)
(34)
And it is only for the Milne model (with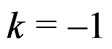 ), one obtains
), one obtains . But the Milne model is empty with
. But the Milne model is empty with ! Even if one would ignore the possibility that the FRW metric subtly represents a vacuum spacetime and which is the reason that there is no density or pressure gradient and there is an universal Newtonian time despite the supposed presence of self-gravity, and even if one will ignore the proof that
! Even if one would ignore the possibility that the FRW metric subtly represents a vacuum spacetime and which is the reason that there is no density or pressure gradient and there is an universal Newtonian time despite the supposed presence of self-gravity, and even if one will ignore the proof that , there are already many suggestion that
, there are already many suggestion that 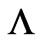 and “Dark Energy” could be illusions created by an inhomogeneous lumpy universe which is significantly different from the simplistic BBM. However if there would be inhomogeneity in a monotonous and continuous manner, there would be a preferred centre of the universe in violation of the “Copernican Principle” of no unique centre. On the other hand, discrete fractal models could still satisfy the Copernican Principle.
and “Dark Energy” could be illusions created by an inhomogeneous lumpy universe which is significantly different from the simplistic BBM. However if there would be inhomogeneity in a monotonous and continuous manner, there would be a preferred centre of the universe in violation of the “Copernican Principle” of no unique centre. On the other hand, discrete fractal models could still satisfy the Copernican Principle.
And if we would apply this condition of no trapped surface formation to the de-Sitter model having
 (35)
(35)
from Equation (32), we will have
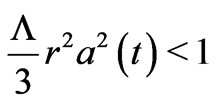 (36)
(36)
In order that this constraint is satisfied, we should have ; and hence, there should not be any mysterious & fictitious Dark Energy.
; and hence, there should not be any mysterious & fictitious Dark Energy.
This result 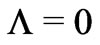 can be also understood from the principle of conservation of energy. By definition, vacuum itself cannot not self-gravitate, and it is matter which self-gravitates. Thus even if vacuum will be assumed to be endowded with an energy density in the form of a
can be also understood from the principle of conservation of energy. By definition, vacuum itself cannot not self-gravitate, and it is matter which self-gravitates. Thus even if vacuum will be assumed to be endowded with an energy density in the form of a , the total energy of the de-Sitter universe will keep on increasing limitlessly because
, the total energy of the de-Sitter universe will keep on increasing limitlessly because  as found in [16]. In order to prevent such runaway violation of energy conservation, one should have
as found in [16]. In order to prevent such runaway violation of energy conservation, one should have 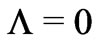 .
.
7. Conclusions
The Big Bang Model intrinsically corresponds to zero pressure. Hence it can neither support any “Dark Energy” nor any heat/radiation; and thus BBM cannot describe the observed universe.
One might also ask whether any model is better than the standard model? True, none is better; indeed the standard model is most developed and most well studied. But that would not mean that we can ignore Equations (5-7) which are consequences of conservation of , i.e., Equation (4). In fact, Equation (5) is a reflection of
, i.e., Equation (4). In fact, Equation (5) is a reflection of  in the spirit of the Einstein Equation. And a Friedmann model with
in the spirit of the Einstein Equation. And a Friedmann model with 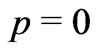 completely fails to describe the observed patch of the universe possessing pressure and radiation.
completely fails to describe the observed patch of the universe possessing pressure and radiation.
Further, the FRW solution may be a mathematical illusion and vacuous with no matter at all: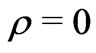 . This could be so because, it has been found that the Schwarzschild Black Hole solution is an illusion because the integration constant appearing there
. This could be so because, it has been found that the Schwarzschild Black Hole solution is an illusion because the integration constant appearing there 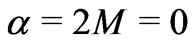 [19]. Similarly, the Oppenheimer Snyder exact solution of Black Hole formation is an illusion as it corresponds to not only
[19]. Similarly, the Oppenheimer Snyder exact solution of Black Hole formation is an illusion as it corresponds to not only 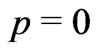 but also
but also 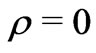 [4]. And actual universe thus must be completely different from the smooth homogeneous fluid picture assumed by the BBM (and many other models). It is quite likely that actual universe is lumpy and discrete at all scales, may be it is an infinite hierarchial fractal. In such a case, one cannot rule out the possibility that cosmic red-shifts arise from some hitherto unknown “tired light” effect [20], and the lumpy discrete universe might be static [21-24]. In particular, the absence of supposed cosmic time dilation effects in the Gamma Ray Bursts poses a serious challenge for the hypothesis of an “expanding universe” [24,25].
[4]. And actual universe thus must be completely different from the smooth homogeneous fluid picture assumed by the BBM (and many other models). It is quite likely that actual universe is lumpy and discrete at all scales, may be it is an infinite hierarchial fractal. In such a case, one cannot rule out the possibility that cosmic red-shifts arise from some hitherto unknown “tired light” effect [20], and the lumpy discrete universe might be static [21-24]. In particular, the absence of supposed cosmic time dilation effects in the Gamma Ray Bursts poses a serious challenge for the hypothesis of an “expanding universe” [24,25].
“We find that the observer frame duration of individual pulses does not increase as a function of redshift as one would expect from the cosmological expansion of a Friedman-Lemaitre-Robertson-Walker Universe. In fact, the duration of individual pulses is seen to decrease as their signal-to-noise decreases with increasing redshift, as only the brightest portion of a high redshift GRB’s light curve is accessible to the detector. The results of our simulation are consistent with the fact that a systematic broadening of GRB durations as a function of redshift has not materialized in either the Swift or Fermi detected GRBs with known redshift” [25].
Note, the farthest GRB detected so far, namely, GRB 090429B has a cosmological red-shift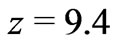 . And yet, it bears no signature of any “expanding universe”.
. And yet, it bears no signature of any “expanding universe”.
8. Endnote
A shorter version of this paper was submitted to Phys. Rev. Lett. in 2009, but the receiving editor refused to process it. Then it was submitted to Phys. Rev. D15; one of Editors and one of the Divisional Associate Editors just vaguely alleged that there could be some error in the derivation of Equation (5), and refused to send it to referees. Then, I prepared a short note dealing only with the derivation of Equation (5) and without mentioning the phrase “FRW Metric” and “Big Bang” (let alone the fact that Equation (5) indicates inapplicability of BBM). First it was sent to Classical & Quantum Gravity as a Research Note and the referee wrote that though it was a correct mathematical exercise, it had no physical relevance. Same thing happened with Gravitation & Cosmology. Then I sent a marginally extended version of it to Pramana, the Indian J. Phys. After 3 months, the referee said that, it should not published because all the mathematical results were already “well known”! And I thank JMP for not only having it properly reviewed but also for waiving the processing charges.
REFERENCES
- A. Mitra, “Revisiting the Old Problem of General Relativistic Adiabatic Collapse of a Uniform Density SelfGravitating Sphere,” Gravitation & Cosmology, Vol. 18, No. 1, 2012, (To Be published).
- A. Mitra, “No Uniform Density Star in General Relativity,” Astrophysics and Space Science, Vol. 333, No. 1, 2010, pp. 169-174. doi:10.1007/s10509-010-0567-8
- A. Mitra, “Why Gravitational Contraction Must Be Accompanied by Emission of Radiation in Both Newtonian and Einstein Gravity,” Physical Review D, Vol. 74, No. 2, 2006, p. 024010. doi:10.1103/PhysRevD.74.024010
- A. Mitra, “The Fallacy of Oppenheimer Snyder Collapse: No General Relativistic Collapse at All, No Black Hole, No Physical Singularity,” Astrophysics and Space Science, Vol. 332, No. 1, 2011 pp. 43-48. doi:10.1007/s10509-010-0578-5
- A. Mitra, “The Matter in the Big-Bang Model Is Dust and Not Any Arbitrary Perfect Fluid!” Astrophysics and Space Science, Vol. 333, No. 1, 2011, pp. 351-356. doi:10.1007/s10509-011-0635-8
- B. F. Schutz, “A First Course in General Relativity,” Cambridge University Press, Cambridge, 1985.
- J. V. Narlikar, “An Introduction to Cosmology,” Cambridge University Press, Cambridge, 2002.
- E. Harrison, “Cosmology, the Science of the Universe,” Cambridge University Press, Cambridge, 2000, p. 349.
- S. A. Hayward, “Gravitational Energy in Spherical Symmetry,” Physical Review D, Vol. 53, No. 4, 1996, pp. 1938- 1949. doi:10.1103/PhysRevD.53.1938
- M. E. Cahill and G. C. McVittie, “Spherical Symmetry and Mass-Energy in General Relativity. II: Particular Cases,” Journal Mathematical Physics, Vol. 11, No. 4, 1970, pp. 1392-1401. doi:10.1063/1.1665274
- A. Mitra, “Macroscopic Form of the First Law of Thermodynamics for an Adibatically Evolving Non-singular Self-gravitating Fluid,” Foundations of Physics, Vol. 41, No. 9, 2011 pp. 1454-1461. doi:10.1007/s10701-011-9557-0
- Yu. V. Baryshev, “Expanding Space: The Root of Conceptual Problems of the Cosmological Physics,” Proceedings of the International Conference on Problems of Practical Cosmology, St. Petersburg, 23-27 June 2008, pp. 20- 30.
- P. J. E. Peebles, “Principles of Physical Cosmology,” Princeton University Press, Priceton, 1993.
- A. Mitra, “Does Pressure Increase or Decrease Active Gravitational Mass Density,” Physics Letters B, Vol. 685, No. 1, 2010, pp. 8-11. doi:10.1016/j.physletb.2010.01.048
- N. Rosen, “The Energy of the Universe,” General Relativity and Gravitation, Vol. 26, No. 3, 1994, pp. 319-321. doi:10.1007/BF02108013
- A. Mitra, “Einstein Energy Associated with the Friedmann-Robertson-Walker Metric,” General Relativity and Gravitation, Vol. 42, No. 3, 2010, pp. 443-469. doi:10.1007/s10714-009-0863-1
- M. Kriele, “A Bound on the Concentration of Mmatter in Spherically Symmetric Stars & Its Application for the Existence of Black-Holes,” Rendiconti del Seminario Matematico Università e Politecnico di Torino, Vol. 50, 1992, pp. 147-152.
- A. Mitra, “Quantum Information Paradox: Real or Fictitious,” Pramana, Vol. 73, No. 3, 2009, pp. 615-622. doi:10.1007/s12043-009-0113-9
- A. Mitra, “Comments on “The Euclidean Gravitational Action as Black Hole Entropy, Singularities, and SpaceTime Voids,” Journal of Mathematical Physics, Vol. 50, No. 4, 2009, p. 042502. doi:10.1063/1.3118910
- Y. A. Yatsunenk and J. A. Budagov, “Red Shift in a Laboratory Environment,” arXiv.org., 2011, arXiv:1103.0808.
- J. G. Hartnett, “Is the Universe Really Expanding?” arXiv. org., 2011, arXiv:1107.24851.
- D. F. Crawford, “Observational Evidence Favors a Static Universe (Part I),” Journal of Cosmology, Vol. 13, 2011, pp. 3875-3946.
- D. F. Crawford, “Observations of Type 1a Supernovae Are Consistent with a Static Universe,” arXiv.org., 2009, (arXiv:0901. 4172).
- D. F. Crawford, “No Evidence of Time Dilation in Gamma Ray Burst Data,” arXiv.org., 2009, (arXiv:0901.4169).
- D. Kocevski and V. Petrosian, “On the Lack of Time Dilation Signatures in Gamma-Ray Burst Light Curves,” The Astrophysical Journal, Submitted 2011, (arXiv: 1110.6175).

